Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-19T18:57:44.663Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Summability and Discrete Weighted Muckenhoupt and Gehring Type Inequalities

Part of: Inequalities Nontrigonometric harmonic analysis Harmonic analysis in several variables Harmonic analysis in one variable

Published online by Cambridge University Press:  11 March 2019

S. H. Saker  and
I. Kubiaczyk
S. H. Saker
Affiliation:
Department of Mathematics, Faculty of Science, Mansoura University, Mansoura 35516, Egypt (shsaker@mans.edu.eg) Faculty of Mathematics and Computer Science, Adam Mickiewicz University, Umultowska 87, 61-614 Poznan, Poland (kuba@amu.edu.pl)
I. Kubiaczyk
Affiliation:
Department of Mathematics, Faculty of Science, Mansoura University, Mansoura 35516, Egypt (shsaker@mans.edu.eg)
Get access Rights & Permissions [Opens in a new window]

Abstract

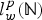In this paper, we prove some reverse discrete inequalities with weights of Muckenhoupt and Gehring types and use them to prove some higher summability theorems on a higher weighted space $l_{w}^{p}({\open N})$ form summability on the weighted space 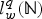$l_{w}^{q}({\open N})$ when p>q. The proofs are obtained by employing new discrete weighted Hardy's type inequalities and their converses for non-increasing sequences, which, for completeness, we prove in our special setting. To the best of the authors' knowledge, these higher summability results have not been considered before. Some numerical results will be given for illustration.

Keywords

reverse Hölder inequalityHardy's type inequalityinterpolationweighted Muckenhoupt's inequalityweighted Gehring's inequalityhigher summability

MSC classification

Primary: 26D07: Inequalities involving other types of functions
Secondary: 42B25: Maximal functions, Littlewood-Paley theory 42C10: Fourier series in special orthogonal functions (Legendre polynomials, Walsh functions, etc.) 42A24: Summability and absolute summability of Fourier and trigonometric series
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 62 , Issue 4 , November 2019 , pp. 949 - 973
Copyright
Copyright © Edinburgh Mathematical Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Asekritova, I., Krugljak, N. Ya., Maligranda, L. and Persson, L. E., Distribution and rearrangement estimates of the maximal function and interpolation, Stud. Math. 124 (1997), 107–132.Google Scholar
2Bastero, J., Milman, M. and Ruiz, F. J., On sharp reiteration theorems and weighted norm inequalities, Stud. Math. 142 (2000), 7–24.Google Scholar
3Bennett, G., Lower bounds for matrices, Linear Algebra Appl. 82 (1986), 81–98.Google Scholar
4Bober, J., Carneiro, E., Hughes, K. and Pierce, L. B., On a discrete version of Tanaka's theorem for maximal functions, Proc. Amer. Math. Soc. 140 (2012), 1669–1680.Google Scholar
5Bojarski, B., Remarks on the stability of reverse Hölder inequalities and quasiconformal mappings, Ann. Acad. Sci. Fenn. Ser. A. I. Math. 10 (1985), 89–94.Google Scholar
6Bojarski, B., Sbordone, C. and Wik, I., The Muckenhoupt class A 1(R), Studia Math. VII 10 (1992), 155–163.Google Scholar
7Carneiro, E. and Hughes, K., On the endpoint regularity of discrete maximal operators, Math. Res. Lett. 19 (2012), 1245–1262.Google Scholar
8Carneiro, E. and Madrid, J., Derivative bounds for fractional maximal functions, Trans. Amer. Math. Soc. 369 (2017), 4063–4092.Google Scholar
9D'Apuzzo, L. and Sbordone, C., Reverse Hölder inequalities, a sharp result, Rend. Mat. Appl. 10 (1990), 357–366.Google Scholar
10Franciosi, M., Weighted rearrangement and higher integrability results, Stud. Math. 92 (1989), 31–39.Google Scholar
11Franciosi, M., On weak reverse integral inequalities for mean oscillations, Proc. Amer. Math. Soc. 113 (1991), 105–112.Google Scholar
12Franciosi, M. and Moscariello, G., Higher integrability results, Manuscripta Math. 52 (1985), 151–170.Google Scholar
13Garling, D. J. H., Inequalities: a journey into linear analysis (Cambridge University Press, 2007).Google Scholar
14Gehring, F. W., The L p-integrability of the partial derivatives of a quasiconformal mapping, Bull. Amer. Math. Soc. 97 (1973), 465–466.Google Scholar
15Gehring, F. W., The L p-integrability of the partial derivatives of a quasi-conformal mapping, Acta Math. 130 (1973), 265–277.Google Scholar
16Hardy, G. H., Littlewood, J. E. and Pólya, G., Some simple inequalities satisfied by convex functions, Messenger Math. 58 (1929), 145–152.Google Scholar
17Hardy, G. H., Littlewood, J. E. and Polya, G., Inequalities, 2nd edn (Cambridge University Press, 1934).Google Scholar
18Herz, C., The Hardy–Littlewood maximal theorems, Symposium on Harmonic Analysis (University of Warwick, 1968).Google Scholar
19Iwaniec, T., On L p-integrability in PDEs and quasiregular mappings for large exponent, Ann. Acad. Sci. Fenn. Ser. A J. Math. 7 (1982), 301–322.Google Scholar
20Korenovskii, A. A., The exact continuation of a reverse Hölder inequality and Muckenhoupt's conditions, Math. Notes 52 (1992), 1192–1201.Google Scholar
21Liu, F., Endpoint regularity of discrete multisublinear fractional maximal operators associated with l 1-balls, J. Ineq. Appl. 2018 (2018), 33.Google Scholar
22Madrid, J., sharp inequalities for the variation of the discrete maximal function, Bull. Aust. Math. Soc. 95 (2017), 94–107.Google Scholar
23Magyar, A., Stein, E. M. and Wainger, S., Discrete analogues in harmonic analysis: spherical averages, Ann. Math. 155 (2002), 189–208.Google Scholar
24Mastylo, M. and Milman, M., A new approach to Gehring's Lemma, Indiana Univ. Math. J. 49 (2000), 655–679.Google Scholar
25Milman, M., A note on Gehring's lemma, Ann. Acad. Sci. Fenn. Ser. A. J. Math. 21 (1996), 389–398.Google Scholar
26Milman, M., A Note on reversed Hardy inequalities and Gehring's lemma, Comm. Pure Appl. Math. 50 (1997), 311–315.Google Scholar
27Muckenhoupt, B., Hardy's inequality with weights, Studia Math. 44 (1972), 31–38.Google Scholar
28Muckenhoupt, B., Weighted norm inequalities for the Hardy maximal function, Trans. Amer. Math. Soc. 165 (1972), 207–226.Google Scholar
29Popoli, A., Optimal integrability in $B_p^q$ classes, Le Matematiche LII (1997), 157–168.Google Scholar
30Renaud, P. F., A reversed Hardy inequality, Bull. Aust. Math. Soc. 34 (1986), 225–232.Google Scholar
31Sbordone, S., Higher integrability from reverse integral inequalities, in Methods of functional analysis and the theory of elliptic equations (ed. D. Greco) Proceedings of the International Meeting Dedicated to the Memory of Professor Carlo Miranda, pp. 347–357 (Liguori, 1982).Google Scholar
32Sbordone, S., Some reverse integral inequalities (Atti Accad. Pontaniana, Napoli, 1984).Google Scholar
33Sbordone, S., Rearrangement of functions and reverse Jensen inequality, Proceedings of Symposia in Pure Mathematics, Volume 45 (American Mathematical Society, Providence RI, 1986), 325–329.Google Scholar
34Stein, E. M. and Wainger, S., Discrete analogues in harmonic analysis I: l 2-estimates for singular Radon transforms, Amer. J. Math. 121 (1999), 1291–1336.Google Scholar
35Stein, E. M. and Wainger, S., Discrete analogues in harmonic analysis II: Fractional integration, J. Anal. Math. 80 (2000), 335–355.Google Scholar
36Stein, E. M. and Wainger, S., Two discrete fractional integral operators revisited, J. Anal. Math. 87 (2002), 451–479.Google Scholar
37Wik, I., Reverse Hölder inequalities with constant close to 1, Ric. Math. 39 (1990), 151–157.Google Scholar