Abstract
Reciprocal best matches play an important role in numerous applications in computational biology, in particular as the basis of many widely used tools for orthology assessment. Nevertheless, very little is known about their mathematical structure. Here, we investigate the structure of reciprocal best match graphs (RBMGs). In order to abstract from the details of measuring distances, we define reciprocal best matches here as pairwise most closely related leaves in a gene tree, arguing that conceptually this is the notion that is pragmatically approximated by distance- or similarity-based heuristics. We start by showing that a graph G is an RBMG if and only if its quotient graph w.r.t. a certain thinness relation is an RBMG. Furthermore, it is necessary and sufficient that all connected components of G are RBMGs. The main result of this contribution is a complete characterization of RBMGs with 3 colors/species that can be checked in polynomial time. For 3 colors, there are three distinct classes of trees that are related to the structure of the phylogenetic trees explaining them. We derive an approach to recognize RBMGs with an arbitrary number of colors; it remains open however, whether a polynomial-time for RBMG recognition exists. In addition, we show that RBMGs that at the same time are cographs (co-RBMGs) can be recognized in polynomial time. Co-RBMGs are characterized in terms of hierarchically colored cographs, a particular class of vertex colored cographs that is introduced here. The (least resolved) trees that explain co-RBMGs can be constructed in polynomial time.









Similar content being viewed by others
Notes
At this point, MH informed the coauthors via git commit from the delivery room that his daughter Lotta Merle was being born.
Best enjoyed with proper soundtrack at https://www.youtube.com/watch?v=XjehlT1VjiU.
References
Aho A, Sagiv Y, Szymanski T, Ullman J (1981) Inferring a tree from lowest common ancestors with an application to the optimization of relational expressions. SIAM J Comput 10:405–421
Altenhoff AM, Boeckmann B, Capella-Gutierrez S, Dalquen DA, DeLuca T, Forslund K, Jaime HC, Linard B, Pereira C, Pryszcz LP, Schreiber F, da Silva AS, Szklarczyk D, Train CM, Bork P, Lecompte O, von Mering C, Xenarios I, Sjölander K, Jensen LJ, Martin MJ, Muffato M, Gabaldón T, Lewis SE, Thomas PD, Sonnhammer E, Dessimoz C (2016) Standardized benchmarking in the quest for orthologs. Nat Methods 13:425–430
Altenhoff AM, Dessimoz C (2009) Phylogenetic and functional assessment of orthologs inference projects and methods. PLoS Comput Biol 5:e1000262
Bork P, Dandekar T, Diaz-Lazcoz Y, Eisenhaber F, Huynen M, Yuan Y (1998) Predicting function: from genes to genomes and back. J Mol Biol 283:707–725
Bretscher A, Corneil D, Habib M, Paul C (2008) A simple linear time LexBFS cograph recognition algorithm. SIAM J Discrete Math 22:1277–1296
Corneil D, Perl Y, Stewart L (1985) A linear recognition algorithm for cographs. SIAM J Comput 14:926–934
Corneil DG, Lerchs H, Steward Burlingham L (1981) Complement reducible graphs. Discr Appl Math 3:163–174
Crespelle C, Paul C (2006) Fully dynamic recognition algorithm and certificate for directed cographs. Discr Appl Math 154:1722–1741
Fitch WM (2000) Homology: a personal view on some of the problems. Trends Genet 16:227–231
Geiß M, Anders J, Stadler PF, Wieseke N, Hellmuth M (2018) Reconstructing gene trees from Fitch’s xenology relation. J Math Biol 77:1459–1491
Geiß M, Chávez E, González M, López A, Valdivia D, Hernández Rosales M, Stadler BMR, Hellmuth M, Stadler PF (2019a) Best match graphs. J Math Biol 78:2015–2057
Geiß M, González Laffitte M, López Sánchez A, Valdivia D, Hellmuth M, Hernández Rosales M, Stadler P (2019b) Best match graphs and reconciliation of gene trees with species trees. Preprint arXiv:1904.12021
Habib M, Paul C (2005) A simple linear time algorithm for cograph recognition. Discrete Appl Math 145:183–197
Hammack R, Imrich W, Klavžar S (2011) Handbook of product graphs, 2nd edn. Discrete mathematics and its applications. CRC Press, Boca Raton
Harary F, Schwenk AJ (1973) The number of caterpillars. Discrete Math 6:359–365
Hellmuth M (2017) Biologically feasible gene trees, reconciliation maps and informative triples. Algorithms Mol Biol 12:23
Hellmuth M, Hernandez-Rosales M, Huber KT, Moulton V, Stadler PF, Wieseke N (2013) Orthology relations, symbolic ultrametrics, and cographs. J Math Biol 66:399–420
Hellmuth M, Marc T (2015) On the Cartesian skeleton and the factorization of the strong product of digraphs. Theor Comp Sci 565:16–29
Hellmuth M, Seemann CR (2019) Alternative characterizations of Fitch’s xenology relation. J Math Biol 79:969–986
Hellmuth M, Stadler PF, Wieseke N (2017) The mathematics of xenology: di-cographs, symbolic ultrametrics, 2-structures and tree-representable systems of binary relations. J Math Biol 75:199–237
Hellmuth M, Wieseke N, Lechner M, Lenhof HP, Middendorf M, Stadler PF (2015) Phylogenetics from paralogs. Proc Natl Acad Sci USA 112:2058–2063
Hernández-Rosales M, Hellmuth M, Wieseke N, Huber KT, Moulton V, Stadler PF (2012) From event-labeled gene trees to species trees. BMC Bioinf 13:S6
Jahangiri-Tazehkand S, Wong L, Eslahchi C (2017) OrthoGNC: a software for accurate identification of orthologs based on gene neighborhood conservation. Genom Proteom Bioinf 15:361–370
Lechner M, Hernandez-Rosales M, Doerr D, Wieseke N, Thévenin A, Stoye J, Hartmann RK, Prohaska SJ, Stadler PF (2014) Orthology detection combining clustering and synteny for very large datasets. PLoS ONE 9:e105015
Li J (2012) Combinatorial logarithm and point-determining cographs. Elec J Comb 19:P8
McKenzie R (1971) Cardinal multiplication of structures with a reflexive relation. Fund Math 70:59–101
Overbeek R, Fonstein M, D’Souza M, Pusch GD, Maltsev N (1999) The use of gene clusters to infer functional coupling. Proc Natl Acad Sci USA 96:2896–2901
Schieber B, Vishkin U (1988) On finding lowest common ancestors: simplification and parallelization. SIAM J Comput 17:1253–1262
Setubal JC, Stadler PF (2018) Gene phyologenies and orthologous groups. In: Setubal JC, Stadler PF, Stoye J (eds) Comparative genomics, vol 1704. Springer, Heidelberg, pp 1–28
Sumner DP (1974) Dacey graphs. J Aust Math Soc 18:492–502
Tatusov RL, Koonin EV, Lipman DJ (1997) A genomic perspective on protein families. Science 278:631–637
Train CM, Glover NM, Gonnet GH, Altenhoff AM, Dessimoz C (2017) Orthologous matrix (OMA) algorithm 2.0: more robust to asymmetric evolutionary rates and more scalable hierarchical orthologous group inference. Bioinformatics 33:i75–i82
Wall DP, Fraser HB, Hirsh AE (2003) Detecting putative orthologs. Bioinformatics 19:1710–1711
Yu C, Zavaljevski N, Desai V, Reifman J (2011) QuartetS: a fast and accurate algorithm for large-scale orthology detection. Nucleic Acids Res 39:e88
Acknowledgements
Partial financial support by the German Federal Ministry of Education and Research (BMBF, Project No. 031A538A, de.NBI-RBC) is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Technical part
Least resolved trees
The understanding of least resolved trees, i.e., the “smallest” trees that explain a given RBMGs relies crucially on the properties of BMGs. We therefore start by recalling some pertinent results by Geiß et al. (2019a).
Lemma 1
Let \((\vec {G},\sigma )\) be a BMG with vertex set L. Then, \(x{\mathsf {R} }y\) implies \(\sigma (x)=\sigma (y)\). In particular, \((\vec {G},\sigma )\) has no arcs between vertices within the same \({\mathsf {R} }\)-class. Moreover, \(N^+(x)\ne \emptyset \), while the in-neighborhood \(N^-(x)\) may be empty for all \(x\in L\).
For an \({\mathsf {R} }\)-class \(\alpha \) of a BMG we define its color \(\sigma (\alpha )=\sigma (x)\) for some \(x\in \alpha \). This is indeed well-defined, since, by Lemma 1, all vertices within \(\alpha \) must share the same color. Definition 9 of Geiß et al. (2019a) is a key construction in the theory of BMGs. It introduces the root\(\rho _{\alpha ,s}\)of an\({\mathsf {R} }\)-class\(\alpha \)with color\(\sigma (\alpha )=r\)w.r.t. a second, different color\(s\ne r\) in a tree \((T,\sigma )\) that explains a BMG \((\vec {G},\sigma )\) by means of the following equation:
where \(\max \) is taken w.r.t. \(\prec _T\). The roots \(\rho _{\alpha ,s}\) are uniquely defined by \((T,\sigma )\) because the color-restricted out-neighborhoods \(N^+_s(\alpha )\) are determined by \((T,\sigma )\) alone. Since \({{\,\mathrm{lca}\,}}(x,y)={{\,\mathrm{lca}\,}}(x,y')\) for any two \(y,y'\in N^+_s(x), x\in \alpha \), Eq. (1) simplifies to
Their most important property (Geiß et al. 2019a, Lemma 14) is
for all \(s\in S{\setminus }\{\sigma (\alpha )\}\).
Relationship between \({\mathsf {R} }\)-classes and their roots. Shown is a tree with leaves from two colors (red and blue) whose leaf set consists of the four \({\mathsf {R} }\)-classes \(\alpha \), \(\alpha '\) (red) and \(\beta \), \(\beta '\) (blue). The inner nodes of the tree corresponding to the roots \(\rho _\alpha \), \(\rho _{\alpha '}\), \(\rho _\beta \) and \(\rho _{\beta '}\) are marked in black. Figure reused from (Geiß et al. 2019a), ©Springer (color figure online)
Least resolved for BMGs are unique Geiß et al. (2019a). Here we consider an analogous concept for RBMGs:
Definition 5
Let \((G,\sigma )\) be an RBMG that is explained by a tree \((T,\sigma )\). An inner edge e is called redundant if \((T_e,\sigma )\) also explains \((G,\sigma )\), otherwise e is called relevant.
The next result gives a characterization of redundant edges:
Lemma 2
Let \((G,\sigma )\) be an RBMG explained by \((T,\sigma )\). An inner edge \(e=uv\) in T is redundant if and only if e satisfies the condition
- (LR)
For all colors \(s\in \sigma (L(T(v)))\cap \sigma (L(T(u)){\setminus } L(T(v)))\) holds that if \(v=\rho _{\alpha ,s}\) for some \({\mathsf {R} }\)-class \(\alpha \in {\mathscr {N}}(\vec {G}(T,\sigma ))\), then \(\rho _{\beta ,\sigma (\alpha )}\prec u\) for every \({\mathsf {R} }\)-class \(\beta \subseteq L(T(u)){\setminus } L(T(v))\) of \(\vec {G}(T,\sigma )\) with \(\sigma (\beta )=s\).
Proof
The \({\mathsf {R} }\)-classes appearing throughout this proof refer to the directed graph \((\vec {G},\sigma )=\vec {G}(T,\sigma )\), and hence are completely determined by \((T,\sigma )\). By definition, any redundant edge of \((T,\sigma )\) is an inner edge, thus we can assume that \(e=uv\) is an inner edge of \((T,\sigma )\) throughout the whole proof.
Suppose that Property (LR) is satisfied. We show [with the help of Eq. (3)] that most neighborhoods in the BMG \((\vec {G},\sigma ):=\vec {G}(T,\sigma )\) remain unchanged by the contraction of e, while those neighborhoods that change do so in such a way that \((T_e,\sigma )\) still explains the RBMG \((G,\sigma )\).
We denote the inner vertex in \(T_e\) obtained by contracting \(e=uv\) again by u. Recall that by convention \(u\succ _T v\) in T. By construction, we have \(L(T(w))=L(T_e(w))\) for all \(w\ne v\) and \({{\,\mathrm{lca}\,}}_{T}(x,y)={{\,\mathrm{lca}\,}}_{T_e}(x,y)\) unless \({{\,\mathrm{lca}\,}}_T(x,y)=v\). Hence, a root \(\rho _{\alpha ,s}\ne v\) of \((T,\sigma )\) is also a root in \(T_e\). Equation (3) thus implies that \(N^+_s(\alpha )\) remains unchanged upon contraction of e whenever \(\rho _{\alpha ,s}\ne v\).
Now let \(\alpha \) and s be such that \(v=\rho _{\alpha ,s}\), thus \(N^+_s(\alpha )=L(T(v))\cap L[s]\) by Eq. (3) and in particular \(s\in \sigma (L(T(v)))\). We distinguish two cases:
(1) If \(s\notin \sigma (L(T(u)){\setminus } L(T(v)))\), then there is no \({\mathsf {R} }\)-class \(\beta \subseteq L(T(u)){\setminus } L(T(v))\) of color s, which implies \(L(T(u))\cap L[s]=L(T(v))\cap L[s]\). Hence, the set \(N^+_s(\alpha )\) remains unaffected by contraction of e.
(2) Assume \(s\in \sigma (L(T(u)){\setminus } L(T(v)))\) and let \(\beta \subseteq L(T(u)){\setminus } L(T(v))\) be an \({\mathsf {R} }\)-class of color \(\sigma (\beta ) = s\). Moreover,Footnote 1 let \(\sigma (\alpha )=r\ne s\). We thus have \(\rho _{\beta ,r}\prec _T u\) by Property (LR). Now, \(N^+_s(\alpha )=L(T(v))\cap L[s]\) and \(\beta \subseteq L(T(u)){\setminus } L(T(v))\) imply \(\beta \cap N^+_s(\alpha )=\emptyset \). Moreover, Eq. (3) and \(\rho _{\beta ,r}\prec _T u\) imply that \(\alpha \cap N^+_r(\beta )=\emptyset \) in \((T,\sigma )\), i.e., \(xy\notin E(G)\) for any \(x\in \alpha \) and \(y\in \beta \) since neither (x, y) nor (y, x) is an arc in \(\vec {G}\). After contraction of e, we have \(\rho _{\beta , r}\prec \rho _{\alpha ,s}\), i.e., \(\beta \subseteq N^+_s(\alpha )\), but \(\alpha \cap N^+_r(\beta )=\emptyset \) in \((T_e,\sigma )\) by Eq. (3). Thus we have \((x,y)\in E(\vec {G})\) and \((y,x)\notin E(\vec {G})\), which implies \(xy\notin E(G(T_e,\sigma ))\). In summary, we can therefore conclude that \((T_e,\sigma )\) still explains \((G,\sigma )\).
Conversely, suppose that e is a redundant edge. If there is no \({\mathsf {R} }\)-class \(\alpha \) with \(v=\rho _{\alpha ,s}\), then Eq. (3) again implies that contraction of e does not affect the out-neighborhoods of any \({\mathsf {R} }\)-classes, thus \((T_e,\sigma )\) explains \((G,\sigma )\). Hence assume, for contradiction, that there is a color \(s\in \sigma (L(T(v)))\cap \sigma (L(T(u)){\setminus } L(T(v)))\) and an \({\mathsf {R} }\)-class \(\beta \subseteq L(T(u)){\setminus } L(T(v))\) of color s with \(\rho _{\beta ,r}\succeq u\), where \(r\in S{\setminus } \{s\}\) such that there exists an \({\mathsf {R} }\)-class \(\alpha \) of color \(\sigma (\alpha )=r\) with \(v=\rho _{\alpha ,s}\). Note that this in particular means that there is no leaf z of color r in \(L(T(u)){\setminus } L(T(v))\) as otherwise \({{\,\mathrm{lca}\,}}(\beta ,z)\prec _T u=\rho _{\beta ,r}={{\,\mathrm{lca}\,}}(\beta ,\alpha )\); a contradiction since \(\alpha \in N_r^+(\beta )\) by Eq. (3). Since by construction \(\alpha \prec v\), we have \(u={{\,\mathrm{lca}\,}}(\alpha ,\beta )\) and therefore \(\rho _{\beta ,r}= u\). In particular, it holds \(\rho _{\beta ,r}\succ \rho _{\alpha ,s}\). As a consequence, we have \(\beta \cap N^+_s(\alpha )=\emptyset \) and \(\alpha \subseteq N^+_r(\beta )\) in \((T,\sigma )\), again by Eq. (3). Thus, for any \(x\in \alpha \) and \(y\in \beta \) we have \((x,y)\notin E(\vec {G})\) and \((y,x)\in E(\vec {G})\), and therefore \(xy\notin E(G)\). Since \(\rho _{\beta ,r}= u\), contraction of e implies \(\rho _{\beta ,r}= \rho _{\alpha ,s}\) in \((T_e,\sigma )\). Therefore, \((x,y)\in E(\vec {G})\) and \((y,x)\in E(\vec {G})\), which implies \(xy\in E(G(T_e,\sigma ))\). Thus \((T_e,\sigma )\) does not explain \((G,\sigma )\); a contradiction. \(\square \)
Note that the characterization of redundant edges requires information on (directed) best matches. In particular, Property (LR) requires \({\mathsf {R} }\)-classes (Fig. 10).
The next result, Lemma 3, provides alternative sufficient conditions for least resolved trees. In particular, it shows whether inner edges uv can be contracted based on the particular colors of leaves below the children of u. We will show in the last section that the conditions in Lemma 3 are also necessary for RBMGs that are cographs (cf. Lemma 46). These conditions are thus designed to fit in well within the framework of RBMGs that are cographs, which will be introduced in more detail later, although these conditions may be relaxed for the general case.
Lemma 3
Let \((G,\sigma )\) be an RBMG explained by \((T,\sigma )\) and let \(e=uv\) be an inner edge of T. Moreover, for two vertices x, y in T, we define \(S_{x,\lnot y}:=\sigma (L(T(x))){\setminus } \sigma (L(T(y)))\). Then \((T_e,\sigma )\) explains \((G,\sigma )\), if one of the following conditions is satisfied:
- (1)
\(\sigma (L(T(v'))) \cap \sigma (L(T(v))) = \emptyset \) for all \(v'\in \mathsf {child} _T(u)\), or
- (2)
\(\sigma (L(T(v'))) \cap \sigma (L(T(v))) \in \{\sigma (L(T(v))),\sigma (L(T(v')))\}\) for all \(v'\in \mathsf {child} _T(u)\), and either
- (i)
\(\sigma (L(T(v)))\subseteq \sigma (L(T(v')))\) for all \(v'\in \mathsf {child} _T(u)\), or
- (ii)
if \(\sigma (L(T(v')))\subsetneq \sigma (L(T(v)))\) for some \(v'\in \mathsf {child} _T(u)\), then, for every \(w\in \mathsf {child} _T(v)\) that satisfies \(S_{w,\lnot v'} \ne \emptyset \), it holds that \(\sigma (L(T(v')))\) and \(\sigma (L(T(w)))\) do not overlap and thus, \(\sigma (L(T(v')))\subseteq \sigma (L(T(w)))\) .
- (i)
Proof
Suppose that \(e=uv\) satisfies one of the Properties (1) or (2). If Property (1) is satisfied, we clearly have \(\sigma (L(T(v)))\cap \sigma (L(T(u)){\setminus } L(T(v)))=\emptyset \), which implies that Condition (LR) of Lemma 2 is trivially satisfied. Therefore, e is redundant in \((T,\sigma )\) and, by Definition 5, \((T_e,\sigma )\) explains \((G,\sigma )\).
Now let \(\sigma (L(T(v'))) \cap \sigma (L(T(v))) \in \{\sigma (L(T(v))),\sigma (L(T(v')))\}\) for all \(v'\in \mathsf {child} _T(u)\) and assume that either Property (2.i) or (2.ii) is satisfied. In order to see that \((T_e,\sigma )\) explains \((G,\sigma )\), we show that e is redundant in \((T,\sigma )\) by application of Lemma 2. Thus suppose \(v=\rho _{\alpha ,s}\) for some \({\mathsf {R} }\)-class \(\alpha \in {\mathscr {N}}(\vec {G}(T,\sigma ))\). If there exists no \({\mathsf {R} }\)-class \(\beta \subseteq L(T(u)){\setminus } L(T(v))\) of \(\vec {G}(T,\sigma )\) with \(\sigma (\beta )=s\), then Lemma 2 is again trivially satisfied and \((T_e,\sigma )\) explains \((G,\sigma )\). Hence, suppose that there is an \({\mathsf {R} }\)-class \(\beta \subseteq L(T(u)){\setminus } L(T(v))\) of \(\vec {G}(T,\sigma )\) with \(\sigma (\beta )=s\). Clearly, if \(\beta \preceq _T x\prec _T u\) for some \(x\in \mathsf {child} _T(u){\setminus } \{v\}\) with \(\sigma (L(T(v)))\subseteq \sigma (L(T(x)))\), then \(\rho _{\beta ,\sigma (\alpha )}\preceq _T x\prec _T u\).
Hence, if Property (2.i) holds, i.e., \(\sigma (L(T(v))) \subseteq \sigma (L(T(v')))\) for all \(v'\in \mathsf {child} _T(u)\), we easily see that for all \({\mathsf {R} }\)-classes \(\beta \subseteq L(T(u){\setminus } T(v))\) with \(\sigma (\beta )=s\) we have \(\rho _{\beta ,\sigma (\alpha )}\preceq _T x\prec _T u\) for some \(x\in \mathsf {child} _T(u){\setminus } \{v\}\). Therefore, e is redundant in \((T,\sigma )\) and \((T_e,\sigma )\) explains \((G,\sigma )\).
Now suppose that Property (2.ii) holds. If \(\sigma (\alpha )\in \sigma (L(T(v')))\) for each \(v'\in \mathsf {child} _T(u)\), we easily see that \(\rho _{\beta ,\sigma (\alpha )}\preceq _T x \prec _T u\) for some \(x\in \mathsf {child} _T(u){\setminus } \{x\}\). Otherwise, there exists some \({\tilde{v}}\in \mathsf {child} _T(u){\setminus } \{v\}\) such that \(\sigma (\alpha )\notin \sigma (L(T({\tilde{v}})))\). By Property (2), \(\sigma (L(T({\tilde{v}})))\) and \(\sigma (L(T(v)))\) do not overlap. Therefore, \(\sigma (L(T({\tilde{v}}))) \subsetneq \sigma (L(T(v)))\). In order to show that (LR) is satisfied, we thus need to show that \(s\notin \sigma (L(T({\tilde{v}})))\), otherwise \(\rho _{\beta ',s}=u\) for some \({\mathsf {R} }\)-class \(\beta ' \subseteq L(T(u)){\setminus } L(T(v))\) of \(\vec {G}(T,\sigma )\). Let \(w\in \mathsf {child} _T(v)\) such that \(a\preceq _T w\) for some \(a\in \alpha \). Since \(\sigma (\alpha )\notin \sigma (L(T({\tilde{v}})))\), it follows \(S_{w,\lnot {\tilde{v}}}\ne \emptyset \). Hence, by Property (2.ii), it must hold \(\sigma (L(T({\tilde{v}})))\subseteq \sigma (L(T(w)))\). Since \(\rho _{\alpha ,s}=v\) by assumption, we necessarily have \(s\notin \sigma (L(T(w)))\) and thus, as \(\sigma (L(T({\tilde{v}})))\subseteq \sigma (L(T(w)))\), we can conclude \(s\notin \sigma (L(T({\tilde{v}})))\). Thus, for all children \(v'\in \mathsf {child} _T(u)\), we either have \(\sigma (\alpha )\in \sigma (L(T(v')))\) or \(\sigma (\alpha ),\sigma (\beta )\not \in \sigma (L(T(v')))\). Now, one can easily see that \(\rho _{\beta ,\sigma (\alpha )}\preceq _T x \prec _T u\) for some \(x\in \mathsf {child} _T(u){\setminus } \{x\}\). Hence, Condition (LR) from Lemma 2 is always satisfied. Therefore, the edge e is redundant in \((T,\sigma )\), i.e., \((T_e,\sigma )\) explains \((G,\sigma )\). \(\square \)
Definition 6
Let \((G,\sigma )\) be an RBMG explained by \((T,\sigma )\). Then \((T,\sigma )\) is least resolved w.r.t.\((G,\sigma )\) if \((T_A,\sigma )\) does not explain \((G,\sigma )\) for any non-empty series of edges A of \((T,\sigma )\).
Figure 1 gives an example of least resolved trees that are not unique. We summarize the discussion as
Theorem 1
Let \((G,\sigma )\) be an RBMG explained by \((T,\sigma )\). Then there exists a (not necessarily unique) least resolved tree \((T_{e_1\dots e_k},\sigma )\) explaining \((G,\sigma )\) obtained from \((T,\sigma )\) by a series of edge contractions \(e_1 e_2 \dots e_k\) such that the edge \(e_1\) is redundant in \((T,\sigma )\) and \(e_{i+1}\) is redundant in \((T_{e_1\dots e_i},\sigma )\) for \(i\in \{1,\dots ,k-1\}\). In particular, \((T,\sigma )\) displays \((T_{e_1\dots e_k},\sigma )\).
Proof
The Theorem follows directly from the definition of least resolved trees and the observation that for any two redundant edges \(e\ne f\) of \((T,\sigma )\), the tree \((T_{ef},\sigma )\) does not necessarily explain \((G,\sigma )\). Clearly, by definition, \((T_{e_1\dots e_k},\sigma )\) is displayed by \((T,\sigma )\). \(\square \)
\({\mathsf {S} }\)-thinness
Figure 2 shows that \(N(a)=N(b)\) does not necessarily imply \(\sigma (a)=\sigma (b)\) for RBMGs. We therefore work here with a color-preserving variant of thinness.
Definition 7
Let \((G,\sigma )\) be an undirected colored graph. Then two vertices a and b are in relation \({\mathsf {S} }\), in symbols \(a{\mathsf {S} }b\), if \(N(a) = N(b)\) and \(\sigma (a) = \sigma (b)\).
An undirected colored graph \((G,\sigma )\) is \({\mathsf {S} }\)-thin if no two distinct vertices are in relation \({\mathsf {S} }\). We denote the \({\mathsf {S} }\)-class that contains the vertex x by [x].
As a consequence of Lemma 1 and the fact that every RBMG \((G,\sigma )\) is the symmetric part of some BMG \(\vec {G}(T,\sigma )\), we obtain
Lemma 4
Let \((G,\sigma )\) be an RBMG, \((T,\sigma )\) a tree explaining \((G,\sigma )\), and \(\vec {G}(T,\sigma )\) the corresponding BMG. Then \(x{\mathsf {R} }y\) in \(\vec {G}(T,\sigma )\) implies that \(x{\mathsf {S} }y\) in \((G,\sigma )\).
The converse of Lemma 4 is not true, however. A counterexample can be found in Fig. 2.
For an undirected colored graph \((G,\sigma )\), we denote by \(G/{\mathsf {S} }\) the graph whose vertex set are exactly the \({\mathsf {S} }\)-classes of G, and two distinct classes [x] and [y] are connected by an edge in \(G/{\mathsf {S} }\) if there is an \(x'\in [x]\) and \(y'\in [y]\) with \(x'y'\in E(G)\). Moreover, since the vertices within each \({\mathsf {S} }\)-class have the same color, the map \(\sigma _{/{\mathsf {S} }}:V(G/{\mathsf {S} }) \rightarrow S\) with \(\sigma _{/{\mathsf {S} }}([x]) = \sigma (x)\) is well-defined.
Lemma 5
\((G/{\mathsf {S} }, \sigma _{/{\mathsf {S} }})\) is \({\mathsf {S} }\)-thin for every undirected colored graph \((G,\sigma )\). Moreover, \(xy\in E(G)\) if and only if \([x][y] \in E(G/{\mathsf {S} })\). Thus, G is connected if and only if \(G/{\mathsf {S} }\) is connected.
Proof
First, we show that \(xy\in E(G)\) if and only if \([x][y] \in E(G/{\mathsf {S} })\). Assume \(xy\in E(G)\). Since G does not contain loops, we have \(x\notin N(x)\). However, \(x\in N(y)\). Therefore, \(N(x)\ne N(y)\) and thus, \([x]\ne [y]\). By definition, thus, \([x][y] \in E(G/{\mathsf {S} })\).
Now assume \([x][y] \in E(G/{\mathsf {S} })\). By construction, there exists \(x'\in [x]\) and \(y'\in [y]\) such that \(x'y'\in E(G)\) and thus \(x'\in N(y') = N(y)\) and \(y'\in N(x') = N(x)\). In particular, \(x'y'\in E(G)\) implies \(\sigma (x')\ne \sigma (y')\) and thus, \(\sigma (x)\ne \sigma (y)\) since by definition all vertices within an \({\mathsf {S} }\)-class are of the same color. Therefore, \(xy\in E(G)\) by definition of \({\mathsf {S} }\)-thinness.
Now suppose, for contradiction, that \((G/{\mathsf {S} },\sigma _{/{\mathsf {S} }})\) is not \({\mathsf {S} }\)-thin. Then, there are two distinct vertices [x], [y] in \(G/{\mathsf {S} }\) that have the same neighbors \([v_1],\dots ,[v_k]\) in \(G/{\mathsf {S} }\) and \(\sigma _{/{\mathsf {S} }}([x]) = \sigma _{/{\mathsf {S} }}([y])\) and, in particular, \(\sigma (x)=\sigma (y)\). From “\(xy\in E(G)\) if and only if \([x][y] \in E(G/{\mathsf {S} })\)” we infer \(N_G(x) = \bigcup _{i=1}^k \bigcup _{v\in [v_i]} \{v\}= N_G(y)\) and thus \([x] = [y]\); a contradiction. Thus, \((G/{\mathsf {S} }, \sigma _{/{\mathsf {S} }})\) must be \({\mathsf {S} }\)-thin. \(\square \)
The map \(\gamma _{{\mathsf {S} }} :V(G) \rightarrow V(G/{\mathsf {S} }): x\mapsto [x]\) collapses all elements of an \({\mathsf {S} }\)-thin class in \((G,\sigma )\) to a single node in \((G_{/{\mathsf {S} }},\sigma _{/{\mathsf {S} }})\). Hence, the \(\gamma _{{\mathsf {S} }}\)-image of a connected component of \((G,\sigma )\) is a connected component in \((G_{/{\mathsf {S} }},\sigma _{/{\mathsf {S} }})\). Conversely, the pre-image of a connected component of \((G_{/{\mathsf {S} }},\sigma _{/{\mathsf {S} }})\) that contains an edge is a single connected component of \((G,\sigma )\). Furthermore, \((G_{/{\mathsf {S} }},\sigma _{/{\mathsf {S} }})\) contains at most one isolated vertex of each color \(r\in S\). If it exists, then its pre-image is the set of all isolated vertices of color r in \((G,\sigma )\); otherwise \((G,\sigma )\) has no isolated vertex of color r.
The next lemma shows how a tree \((T,\sigma )\) that explains an RBMG \((G,\sigma )\) can be modified to a tree that still explains \((G,\sigma )\) by replacing edges that are connected to vertices within the same \({\mathsf {S} }\)-class. Although this lemma is quite intuitive, one needs to be careful in the proof since changing edges in \((T,\sigma )\) may also change the neighborhoods \(N_G(x)\) of vertices \(x\in V(G)\) and may result in a tree that does not explain \((G,\sigma )\) anymore.
Lemma 6
Let \((G,\sigma )\) be an RBMG that is explained by \((T,\sigma )\) on L. Let \(x,x'\in [x]\) be two distinct vertices in an \({\mathsf {S} }\)-class [x] of \((G,\sigma )\). Suppose that x and \(x'\) have distinct parents \(v_x\) and \(v_{x'}\) in T, respectively. Denote by \(T_{x',v_x}\) the tree on L obtained from T by (i) removing the edge \((v_{x'},x')\), (ii) suppressing the vertex \(v_{x'}\) if it now has degree 2, and (iii) inserting the edge \((v_{x},x')\). Then, \((T_{x',v_x},\sigma )\) explains \((G,\sigma )\).
Proof
Let [x] be an \({\mathsf {S} }\)-class with vertices \(x,x'\in [x]\) that have distinct parents \(v_x\) and \(v_{x'}\) in T, respectively. Put \(T' = T_{x',v_x}\) and let \((G',\sigma )\) be the RBMG explained by \((T',\sigma )\). We proceed with showing that \((G',\sigma )=(G,\sigma )\). To see this, we observe that \(x,x'\in [x]\) implies that \(N_G(x) = N_G(x')\) and \(\sigma (x)=\sigma (x')\). By construction we also have \(N_{G'}(x)=N_{G'}(x')\) and \(x'\notin N_{G'}(x)\). Moving \(x'\) in T does not affect the last common ancestors of x and any \(y\ne x'\), hence \(N_{G'}(x)=N_{G}(x)\), and thus also \(N_{G'}(x')=N_{G}(x)\). Now consider \(N_{G'}(y)\) and \(N_{G}(y)\) for some \(y\ne x,x'\) and assume, for contradiction, that \(N_{G'}(y) \ne N_{G}(y)\). Then there exists a vertex \(z\in N_{G}(y){\setminus } N_{G'}(y)\) or \(z\in N_{G'}(y){\setminus } N_{G}(y)\), which in particular implies \(N_G(z)\ne N_{G'}(z)\). As shown above, \(N_{G'}(x)=N_{G}(x) = N_{G}(x') = N_{G'}(x')\). Hence, \(N_G(z)\ne N_{G'}(z)\) implies \(z\ne x,x'\). Moreover, since z is adjacent to y in either G or \(G'\), we have \(\sigma (z)\ne \sigma (y)\). However, replacing \(x'\) in T cannot influence the adjacencies between vertices u and v with \(\sigma (u)\ne \sigma (x')\) and \(\sigma (v)\ne \sigma (x')\). Taken the latter arguments together, we can conclude that \(\sigma (z) = \sigma (x)\ne \sigma (y)\).
First assume \(z\in N_{G}(y){\setminus } N_{G'}(y)\). Then
Since \(z\notin N_{G'}(y)\), we additionally have
The fact that T and \(T'\) are identical up to the location of \(x'\) together with \(\sigma (z')=\sigma (x')\ne \sigma (y)\) and \(x'\ne z\) implies that in \(T'\) we still have \({{\,\mathrm{lca}\,}}_{T'}(z,y) \preceq _{T'} {{\,\mathrm{lca}\,}}_{T'}(z,y')\) for all \(y'\) with \(\sigma (y') = \sigma (y)\). Hence, Eq. (6) must be satisfied. Eq. (4) and (6) together imply that \(x'=z'\) and that \(x'\) is the only vertex that satisfies Eq. (6). In \(T'\) the vertices x and \(x'\) have the same parent. Together with \(x'=z'\) and Eq. (6) this implies \({{\,\mathrm{lca}\,}}_{T'}(x,y) = {{\,\mathrm{lca}\,}}_{T'}(x',y) \prec _{T'} {{\,\mathrm{lca}\,}}_{T'}(z,y)\). Since T and \(T'\) are identical up to the location of \(x'\), we also have \({{\,\mathrm{lca}\,}}_{T'}(x,y) = {{\,\mathrm{lca}\,}}_{T}(x,y)\) and \({{\,\mathrm{lca}\,}}_{T'}(y,z) = {{\,\mathrm{lca}\,}}_{T}(y,z)\). Combining these arguments, we obtain \({{\,\mathrm{lca}\,}}_{T}(x,y) \prec _{T} {{\,\mathrm{lca}\,}}_{T}(y,z)\), which contradicts Eq. (4) because \(\sigma (z) = \sigma (x)\).
Assuming \(z\in N_{G'}(y){\setminus } N_{G}(y)\), and interchanging the role of T and \(T'\) in the argument above, we obtain
and that there is no other vertex \(z^*\ne x'\) with \(\sigma (z^*)=\sigma (x')\) and \({{\,\mathrm{lca}\,}}_T(z,y) \succ _T {{\,\mathrm{lca}\,}}_T(z^*,y)\). Since x and \(x'\) have the same parent in \(T'\) we have \({{\,\mathrm{lca}\,}}_T(x,y) = {{\,\mathrm{lca}\,}}_{T'}(x,y) = {{\,\mathrm{lca}\,}}_{T'}(x',y) \succeq _{T'} {{\,\mathrm{lca}\,}}_{T'}(z,y)={{\,\mathrm{lca}\,}}_{T}(z,y) \succ _T {{\,\mathrm{lca}\,}}_T(x',y)\). The fact that T and \(T'\) are identical up to the location of \(x'\) now implies that for all inner vertices v, w of \(T'\) we have \(v\prec _{T'}w\) if and only if \(v\prec _T w\). Hence we have
implying that T displays the triple \(x'y|x\). Therefore xy is not an edge in \((G,\sigma )\), whence \(y\notin N_G(x) = N_G(x')\).
Since there is no other vertex \(z^*\ne x'\) with \(\sigma (z^*)=\sigma (x')\) and \({{\,\mathrm{lca}\,}}_T(z,y) \succ _T {{\,\mathrm{lca}\,}}_T(z^*,y)\), we have \({{\,\mathrm{lca}\,}}_T(z^*,y) \succ _T {{\,\mathrm{lca}\,}}_T(x',y)\) for all \(z^*\ne x'\) with \(\sigma (z^*)=\sigma (z)=\sigma (x')\). Since \(y\notin N_G(x')\), there must be a vertex \(y'\) with \(\sigma (y')=\sigma (y)\) such that \({{\,\mathrm{lca}\,}}_T(x',y)\succ _T {{\,\mathrm{lca}\,}}_T(x',y')\). We can choose \(y'\) such that there is no other vertex \(y^*\ne y'\) satisfying \(\sigma (y^*)=\sigma (y')\) and \({{\,\mathrm{lca}\,}}_T(x',y') \succ _T {{\,\mathrm{lca}\,}}_T(x',y^*)\). Thus we have
which implies \(y'\not \in N_G(x)\). However, since \(x'\) is unique w.r.t. Eq. (8), we must have \(y'\in N_G(x')\); a contradiction to \(N_G(x)=N_G(x')\).
Therefore, we have \(N_G(v) = N_{G'}(v)\) for all \(v\in V(G)\), and thus \((G,\sigma )=(G',\sigma )\) as claimed. \(\square \)
Lemma 7
\((G,\sigma )\) is an RBMG if and only if \((G/{\mathsf {S} }, \sigma _{/{\mathsf {S} }})\) is an RBMG. Moreover, every RBMG \((G,\sigma )\) is explained by a tree \(({\widehat{T}},\sigma )\) in which any two vertices \(x,x'\in [x]\) of each \({\mathsf {S} }\)-class [x] of \((G,\sigma )\) have the same parent.
Proof
Consider an RBMG \((G,\sigma )\) explained by the tree \((T,\sigma )\), and let [x] be an \({\mathsf {S} }\)-class of \((G,\sigma )\). If all the vertices within [x] have the same parent v in T, then we can identify the edges \(vx'\) for all \(x'\in [x]\) to obtain the edge v[x]. If all children of v are leaves of the same color, we additionally suppress v in order to obtain a phylogenetic tree T / [x]. Note that in this case, \(\mathsf {par} (v)\) cannot be incident to any leaf y of color \(\sigma (x)\) in \((T,\sigma )\) as this would imply \(N(x)=N(y)\) and therefore \(x{\mathsf {S} }y\). Hence, suppression of v has no effect on any of the neighborhoods and thus does not affect any of the reciprocal best matches in \((T,\sigma )\). If all \({\mathsf {S} }\)-classes are of this form, then the tree \((T/{\mathsf {S} },\sigma _{/{\mathsf {S} }})\) obtained by collapsing each class [x] to a single leaf and potential suppression of 2-degree nodes still explains \((G/{\mathsf {S} },\sigma _{/{\mathsf {S} }})\).
The construction of \(T_{x',v_x}\) as in Lemma 6 can be repeated until all vertices \(x'\) of each \({\mathsf {S} }\)-class [x] have been re-attached to have the same parent \(v_x\). After each re-attachment step, the tree still explains \((G,\sigma )\). The procedure stops when all \(x'\in [x]\) are siblings of x in the tree, i.e., a tree \(({\widehat{T}},\sigma )\) of the desired form is reached. The tree obtained by retaining only one representative of each \({\mathsf {S} }\)-class [x] (relabeled as [x]), explains \((G/{\mathsf {S} }, \sigma _{/{\mathsf {S} }})\).
Conversely, assume that \((G/{\mathsf {S} }, \sigma _{/{\mathsf {S} }})\) is an RBMG explained by the tree \(({\tilde{T}},\sigma _{/{\mathsf {S} }})\). Each leaf in \({\tilde{T}}\) is an \({\mathsf {S} }\)-class [x]. Consider the tree \((T,\sigma )\) obtained by replacing, for all \({\mathsf {S} }\)-classes [x] the edge \(\mathsf {par} ([x])[x]\) in T by the edges \(\mathsf {par} ([x])x'\) and setting \(\sigma (x') = \sigma _{/{\mathsf {S} }}([x])\) for all \(x'\in [x]\). By construction, \((T,\sigma )\) explains \((G,\sigma )\), and thus \((G,\sigma )\) is an RBMG. \(\square \)
Lemma 7 is illustrated in Fig. 3.
Lemma 8
Let \((G,\sigma )\) be an \({\mathsf {S} }\)-thin n-RBMG explained by \((T,\sigma )\) with \(n\ge 2\). Then \(|\sigma (L(T(v)))|\ge 2\) holds for every inner vertex \(v\in V^0(T)\).
Proof
Let \(S=\sigma (V(G))\). Assume, for contradiction, that there exists an inner vertex \(v\in V^0(T)\) such that \(\sigma (L(T(v)))=\{r\}\) with \(r\in S\). Since \((T,\sigma )\) is phylogenetic, there must be two distinct leaves \(a,b\in L(T(v))\) with \(\sigma (a)=\sigma (b)=r\). Since \((G,\sigma )\) is \({\mathsf {S} }\)-thin, a and b do not belong to the same \({\mathsf {S} }\)-class. Hence, \(\sigma (a)=\sigma (b)\) implies \(N(a)\ne N(b)\). Since \(|S|\ge 2\), there is a leaf \(c\in V(G)\) with \(\sigma (c)=s\in S{\setminus } \{r\}\). On the other hand, \(\sigma (L(T(v)))=\{r\}\) implies \({{\,\mathrm{lca}\,}}(a,c)={{\,\mathrm{lca}\,}}(b,c)\succ v\).
Now consider the corresponding BMG \(\vec {G}(T,\sigma )\). Since \(\sigma (L(T(v)))=\{r\}\), we have \(c\in N^-(a)\) if and only if \(c\in N^-(b)\), and \(c\in N^+(a)\) if and only if \(c\in N^+(b)\). Together, this implies \(N(a)=N(b)\) in \(G(T,\sigma )\) ; a contradiction. \(\square \)
Any two leaves x, y in \((T,\sigma )\) with \(\sigma (x)=\sigma (y)\) and \(\mathsf {par} (x)=\mathsf {par} (y)\) obviously belong to the same \({\mathsf {S} }\)-equivalence class of \(G(T,\sigma )\). The absence of such pairs of vertices in \((T,\sigma )\) is thus a necessary condition for \(G(T,\sigma )\) to be \({\mathsf {S} }\)-thin, it is not sufficient, however. We leave it as an open question for future research to characterize the leaf-colored trees that explain \({\mathsf {S} }\)-thin RBMGs.
Connected components, forks, and color-complete subtrees
Although RBMGs, like BMGs, are not hereditary, they satisfy a related, weaker property that will allow us to restrict our attention to connected RBMGs.
Lemma 9
Let \((G,\sigma )\) be an RBMG with vertex set L explained by \((T,\sigma )\) and let \((T_{|L'},\sigma _{|L'})\) be the restriction of \((T,\sigma )\) to \(L'\subseteq L\). Then the induced subgraph \((G,\sigma )[L']:=(G[L'],\sigma _{|L'})\) of \((G,\sigma )\) is a (not necessarily induced) subgraph of \(G(T_{|L'},\sigma _{|L'})\).
Proof
Lemma 1 in (Geiß et al. 2019a) states the analogous result for BMGs. It obviously remains true for the symmetric part. \(\square \)
The next result is a direct consequence of Lemma 9 that will be quite useful for proving some of the following results.
Corollary 1
Let \((G,\sigma )\) be an RBMG that is explained by \((T,\sigma )\). Moreover, let \(v\in V(T)\) be an arbitrary vertex and \((G^*_v,\sigma ^*_v)\) be a connected component of \(G(T(v), \sigma _{|L(T(v))})\). Then, \((G^*_v,\sigma ^*_v)\) is contained in a connected component \((G^*,\sigma ^*)\) of \((G,\sigma )\).
We next ensure the existence of certain types of edges in any RBMG.
Lemma 10
Let \((T,\sigma )\) be a leaf-colored tree on L and let \(v\in V(T)\). Then, for any two distinct colors \(r,s\in \sigma (L(T(v)))\), there is an edge \(xy\in E(G(T,\sigma ))\) with \(x\in L[r]\cap L(T(v))\) and \(y\in L[s]\cap L(T(v))\). In particular, all edges in \(G(T(v), \sigma _{|L(T(v))})\) are contained in \(G(T,\sigma )\).
Proof
Let v be a vertex of \((T,\sigma )\) such that \(r,s\in \sigma (L(T(v)))\), \(r\ne s\). Then there is always an inner vertex \(w\preceq _T v\) such that (i) \(\{r,s\}\subseteq \sigma (L(T(w)))\) and (ii) none of its children \(w_i\in \mathsf {child} (w)\) satisfies \(\{r,s\}\subseteq \sigma (L(T(w_i)))\). Any such w has children \(w_r,w_s\in \mathsf {child} (w)\) such that \(r\in \sigma (L(T(w_r)))\), \(s\notin \sigma (L(T(w_r)))\) and \(s\in \sigma (L(T(w_s)))\), \(r\notin \sigma (L(T(w_s)))\). Thus \({{\,\mathrm{lca}\,}}_T(x,y)\succeq _T w\) for every \(x\in L(T(w_r))\cap L[r]\ne \emptyset \) and \(y\in L[s]\), with equality whenever \(y\in L(T(w_s))\). Analogously, \({{\,\mathrm{lca}\,}}_T(y,x)\succeq _T w\) for every \(y\in L(T(w_s))\cap L[s]\ne \emptyset \) and \(x\in L[r]\), with equality whenever \(x\in L(T(w_r))\). Hence xy is a reciprocal best match mediated by \({{\,\mathrm{lca}\,}}_T(x,y)=w\) whenever \(x\in L(T(w_r))\cap L[r]\) and \(y\in L(T(w_s))\cap L[s]\). Therefore \(xy\in E(G(T,\sigma ))\).
In particular, the latter construction shows that the chosen leaves \(x\in L(T(w_r))\cap L[r]\) and \(y\in L(T(w_s))\cap L[s]\) are reciprocal best matches in \((T(v), \sigma _{|L(T(v))})\). Hence, every edge in \(G(T(v), \sigma _{|L(T(v))})\) is also contained in \(G(T,\sigma )\). \(\square \)
As a direct consequence of Lemma 10, we obtain
Corollary 2
If \((G,\sigma )\) is an RBMG with \(|S|\ge 2\) colors, then there is at least one edge \(xy\in E(G[L[r]\cup L[s]])\) for any two distinct colors \(r, s\in S\).
Theorem 2
Let \((G^*,\sigma ^*)\) with vertex set \(L^*\) be a connected component of some RBMG \((G,\sigma )\) and let \((T,\sigma )\) be a leaf-colored tree explaining \((G,\sigma )\). Then, \((G^*,\sigma ^*)\) is again an RBMG and is explained by the restriction \((T_{|L^*},\sigma _{|L^*})\) of \((T,\sigma )\) to \(L^*\).
Proof
Throughout this proof, all \(N^{+}\)-neighborhoods are taken w.r.t. the underlying BMG \(\vec {G}(T,\sigma )\). It suffices to show that \(G(T_{|L^*},\sigma _{|L^*})=(G^*,\sigma ^*)\). Lemma 9 implies that \((G^*,\sigma ^*)\) is a (not necessarily induced) subgraph of \(G(T_{|L^*},\sigma _{|L^*})\), i.e., \(E(G^*)\subseteq E(G(T_{|L^*},\sigma _{|L^*}))\). By assumption, \((G^*,\sigma ^*)\) is an induced subgraph of \((G,\sigma )\). Thus, we only need to prove that \(E(G(T_{|L^*},\sigma _{|L^*}))\subseteq E(G^*)\).
Assume, for contradiction, that there exists an edge xy in \(G(T_{|L^*},\sigma _{|L^*})\) that is not contained in \((G^*,\sigma ^*)\). By definition, \(r:=\sigma (x) \ne s:=\sigma (y)\) and, in particular, \(x,y\in L^*\). Let \(u:={{\,\mathrm{lca}\,}}_T(x,y)\). By construction, any two vertices within \(L^*\) have the same last common ancestor in \((T,\sigma )\) and \((T_{|L^*},\sigma _{|L^*})\). Since the edge xy is not contained in \((G^*,\sigma ^*)\), the edge xy is not contained in \((G,\sigma )\) either. Hence, x and y do not form reciprocal best matches in \((T,\sigma )\). Thus, there must exist some \(x'\in L[r]\) with \({{\,\mathrm{lca}\,}}_T(x',y)\prec _T {{\,\mathrm{lca}\,}}_T(x,y)\), or a leaf \(y'\in L[s]\) with \({{\,\mathrm{lca}\,}}_T(x,y')\prec _T {{\,\mathrm{lca}\,}}_T(x,y)\).
W.l.o.g. we assume that the first case is satisfied. Since \({{\,\mathrm{lca}\,}}_T(x',y)\prec _T {{\,\mathrm{lca}\,}}_T(x,y)\), we must have \(x'\in L{\setminus } L^*\), as otherwise, \({{\,\mathrm{lca}\,}}_{T_{|L^*}}(x',y)\prec _{T_{|L^*}} {{\,\mathrm{lca}\,}}_{T_{|L^*}}(x,y)\) and hence, x cannot be a best match of y, which in turn would imply that xy is not an edge in \(G(T_{|L^*},\sigma _{|L^*})\). We will re-use the latter argument and refer to it as Argument-1.
In the following, w.l.o.g. we choose \(x'\in L[r]\) such that \({{\,\mathrm{lca}\,}}_T(x',y)\prec _T {{\,\mathrm{lca}\,}}_T(x,y)\) and \({{\,\mathrm{lca}\,}}(x',y)\) is \(\preceq _T\)-minimal among all least common ancestors that satisfy the latter condition. We write \(v:={{\,\mathrm{lca}\,}}_T(x',y)\). By construction, we have \(v\prec _T u\). By contraposition of Argument-1, we have for all \(x''\in L^*\) with \(\sigma (x'') = r\) it must hold that \({{\,\mathrm{lca}\,}}_T(x'',y)\succeq _T {{\,\mathrm{lca}\,}}_T(x,y)\) and thus, \(x''\notin L(T(v))\). In other words, we have
Let \(v_{x'},v_y\in \mathsf {child} (v)\) with \(x'\preceq _T v_{x'}\) and \(y\preceq _T v_y\). The choice of \(x'\) and the resulting \(\preceq _T\)-minimality of \({{\,\mathrm{lca}\,}}(x',y)\) implies that \(\sigma (x)=r\notin \sigma (L(T(v_y)))\). Therefore, \(x'\in N^+_r(y)\). We observe that \(x'y\notin E(G)\) since, otherwise, \(x'\in L^*\); a contradiction. From \(x'y\notin E(G)\) we conclude \(y\notin N^+_s(x')\) and thus there exists an \(y'\in L[s]\) such that \({{\,\mathrm{lca}\,}}_T(x',y')\prec _T {{\,\mathrm{lca}\,}}_T(x',y)=v\) and hence, \(y'\prec _T v_{x'}\).
The latter, in particular implies that \(r,s\in \sigma (L(T(v_{x'}))\). Hence, we can apply Lemma 10 to conclude that there are two vertices \({\tilde{x}}\in L[r]\cap L(T(v_{x'}))\) and \({\tilde{y}}\in L[s]\cap L(T(v_{x'}))\) such that \({\tilde{x}}{\tilde{y}}\in E(G)\). Equation (10) now implies \({\tilde{x}} \notin L^*\). Therefore, \({\tilde{x}}{\tilde{y}}\in E(G)\) now allows us to conclude that \({\tilde{y}}\in L{\setminus } L^*\).
Now, let \({\mathcal {P}}_{xy}=(x=a_0a_1a_2\dots a_{k-1} a_{k}=y)\) be a shortest path in \((G^*, \sigma ^*)\) connecting x and y. Since x and y reside within the same connected component \((G^*, \sigma ^*)\) of \((G,\sigma )\) and \(xy\notin E(G^*)\), such a path exists and, in particular, it must contain at least one \(a_i\ne x,y\), i.e., \(k>1\). By definition of a shortest path, \(a_ia_j\notin E(G)\) for all \(i,j\in \{0,1,\dots , k\}\) that satisfy \(|i-j|>1\). Since \(a_i\in L^*\) for any \(0\le i \le k\) but \({\tilde{x}},{\tilde{y}}\in L{\setminus } L^*\), we have
for any \(0\le i \le k\), since otherwise, \({\tilde{x}}\) and \({\tilde{y}}\) would be contained in the connected component \((G^*,\sigma ^*)\) and thus, also in \(L^*\); a contradiction.
We proceed to show by induction that
- (I1)
\(a_i\in L(T(v))\), \(1\le i \le k\), and
- (I2)
there exists a vertex \({\tilde{a}}_i \in L(T(v))\cap L[\sigma (a_i)]\) such that \({\tilde{a}}_i\notin L^*\), \(1\le i \le k\).
We start with \(i=k\). By construction, \(y=a_{k}\in L(T(v))\) satisfies Property (I1). Moreover, \({\tilde{a}}_{k} :={\tilde{y}}\) satisfies Property (I2). For the induction step assume that, for a fixed \(m\le k\), Property (I1) and (I2) is satisfied for all i with \(m < i\le k\).
Now, consider the case \(i=m\). For better readability we put \(b:=a_{m+1}\) and \({\tilde{b}}:={\tilde{a}}_{m+1}\). By induction hypothesis, b and \({\tilde{b}}\) satisfy Property (I1) and (I2), respectively. Since \(a_m b\in E(G)\), we know that \(\sigma (a_m)\ne \sigma (b)\). In what follows, we consider the two exclusive cases: either \(\sigma (a_m)=\sigma (x) = r\) or \(\sigma (a_m)\ne r\). If \(\sigma (a_m) = r\), then we put \({\tilde{a}}_m = {\tilde{x}}\). Hence, Property (I2) is trivially satisfied for \({\tilde{a}}_m\). Moreover, \(a_m\) must then be contained in L(T(v)), otherwise \(v\succeq _T{{\,\mathrm{lca}\,}}_T(b,{\tilde{x}})\) implies that \({{\,\mathrm{lca}\,}}_T(b,{\tilde{x}})\prec _T {{\,\mathrm{lca}\,}}(b,a_m)\), which contradicts \(a_m b\in E(G)\), i.e., Property (I1) is satisfied as well.
In case \(\sigma (a_m)\ne r\) assume first, for contradiction, that \(a_m\notin L(T(v))\). Since \(b,{\tilde{b}} \in L(T(v))\) we observe that \({{\,\mathrm{lca}\,}}_T(b,a_m)={{\,\mathrm{lca}\,}}_T({\tilde{b}},a_m) \succ _T v\). Note that we have \(b\in N^+_{\sigma (b)}(a_m)\) since \(ba_m\in E(G)\) by definition of \({\mathcal {P}}_{xy}\). Thus, \({{\,\mathrm{lca}\,}}_T(b,a_m)={{\,\mathrm{lca}\,}}_T({\tilde{b}},a_m)\) implies \({\tilde{b}}\in N^+_{\sigma (b)}(a_m)\). Since \(a_m\in L^*\) (by definition) and \({\tilde{b}}\notin L^*\) (by Property (I2)), we can conclude that \(a_m{\tilde{b}}\notin E(G)\). The latter two arguments imply that \(a_m \notin N^+_{\sigma (a_m)}({\tilde{b}})\). Hence, there exists a leaf \(a_m'\) with \(\sigma (a_m)=\sigma (a_m')\) such that \({{\,\mathrm{lca}\,}}_T({\tilde{b}}, a_m')\prec _T {{\,\mathrm{lca}\,}}_T({\tilde{b}}, a_m)\). There are two cases, either \(a_m'\in L(T(v_{{\tilde{b}}}))\) or \(a_m'\notin L(T(v_{{\tilde{b}}}))\), where \(v_{{\tilde{b}}}\in \mathsf {child} (v)\) with \({\tilde{b}} \preceq _T v_{{\tilde{b}}}\). If \(a_m'\in L(T(v_{{\tilde{b}}}))\), then \({{\,\mathrm{lca}\,}}_T(b, a_m')\preceq _T v\) and we can re-use the fact \({{\,\mathrm{lca}\,}}_T(b,a_m) \succ _T v\) from above to conclude that \({{\,\mathrm{lca}\,}}_T(b,a_m')\prec _T {{\,\mathrm{lca}\,}}_T(b,a_m)\). If \(a_m'\notin L(T(v_{{\tilde{b}}}))\), then \({{\,\mathrm{lca}\,}}_T(b,a_m')\preceq _T{{\,\mathrm{lca}\,}}_T({\tilde{b}}, a_m')\). Thus, we have \({{\,\mathrm{lca}\,}}_T(b,a_m')\preceq _T{{\,\mathrm{lca}\,}}_T({\tilde{b}}, a_m')\prec _T {{\,\mathrm{lca}\,}}_T({\tilde{b}}, a_m) = {{\,\mathrm{lca}\,}}_T(b, a_m)\). Hence, in either case we obtain \({{\,\mathrm{lca}\,}}_T(b,a_m')\prec _T {{\,\mathrm{lca}\,}}_T(b,a_m)\), thus \(a_mb\notin E(G)\); a contradiction. Therefore, \(a_m\in L(T(v))\), i.e., Property (I1) is satisfied by \(a_m\).
To summarize the argument so far, Property (I1) is always satisfied for \(a_m\), independent of the particular color \(\sigma (a_m)\). Moreover, Property (I2) is satisfied, in case \(\sigma (a_m) = r\). Thus, it remains to show that Property (I2) is also satisfied in case \(\sigma (a_m)\ne r\). To this end, let \(v_m\in \mathsf {child} (v)\) such that \(a_m\preceq _T v_m\). If \(r\in \sigma (L(T(v_m)))\), then Lemma 10 implies that there must exist leaves \({\tilde{x}}_m, {\tilde{a}}_m \in L(T(v_m))\) with \(\sigma ({\tilde{x}}_m)=r\) and \(\sigma ({\tilde{a}}_m)=\sigma (a_m)\) such that \({\tilde{x}}_m {\tilde{a}}_m \in E(G)\). By Eq. (10), no vertex in \(L(T(v))\cap L[r]\) is contained in \(L^*\), and thus, we have \({\tilde{x}}_m \notin L^*\) and, since \({\tilde{x}}_m {\tilde{a}}_m \in E(G)\), it must also hold \({\tilde{a}}_m \notin L^*\).
Otherwise, if \(r\notin \sigma (L(T(v_m)))\), then \(\sigma ({\tilde{x}}) = r\) and \({\tilde{x}}\preceq _T v_{x'}\) implies that \(v_m\ne v_{x'}\). Hence, \({{\,\mathrm{lca}\,}}(a_m, {\tilde{x}})=v\). In particular, there is no vertex \(x''\in L[r]\) such that \({{\,\mathrm{lca}\,}}_T(a_m,x'')\prec _T{{\,\mathrm{lca}\,}}(a_m, {\tilde{x}})=v\), thus \({\tilde{x}}\in N^+_r(a_m)\). Since \(a_m\in L^*\) and \({\tilde{x}}\notin L^*\), it must hold that \(a_m {\tilde{x}}\notin E(G)\). Thus, there must exist a leaf \({\tilde{a}}_m \in L[\sigma (a_m)]\) such that \({{\,\mathrm{lca}\,}}_T({\tilde{x}}, {\tilde{a}}_m)\prec _T {{\,\mathrm{lca}\,}}_T({\tilde{x}}, a_m)=v\), i.e., \(\sigma (a_m)\in \sigma (L(T(v_{x'})))\). We can therefore apply Lemma 10 to conclude that there must exist \({\tilde{x}}_m \in L(T(v_{x'})) \cap L[r]\) and \({\tilde{a}}_m \in L(T(v_{x'})) \cap L[\sigma (a_m)]\) such that \({\tilde{x}}_m {\tilde{a}}_m \in E(G)\). Analogous argumentation as in the case \(r\in \sigma (L(T(v_m)))\) shows \({\tilde{x}}_m, {\tilde{a}}_m \notin L^*\). Hence, Property (I2) is satisfied, which completes the induction proof.
Property (I1) finally implies that \(a_1 \in L(T(v))\). Moreover, by construction of \({\mathcal {P}}_{xy}\) we have \(xa_1\in E(G^*)\). Property (11), on the other hand, implies \({\tilde{x}}a_1\notin E(G^*)\). Consequently, we have \({{\,\mathrm{lca}\,}}_T(a_1,x)\prec _T {{\,\mathrm{lca}\,}}_T(a_1,{\tilde{x}})\). This, however, contradicts \({{\,\mathrm{lca}\,}}_T(a_1,x) = u \succ _T v = {{\,\mathrm{lca}\,}}_T(a_1,{\tilde{x}})\). The shortest path \({\mathcal {P}}_{xy}\) can, therefore, consist only of the single edge xy, and hence \(E(G(T_{|L^*},\sigma _{|L^*}))\subseteq E(G^*)\). Therefore \(G(T_{|L^*},\sigma _{|L^*})=(G^*,\sigma ^*)\) and \((T_{|L^*},\sigma _{|L^*})\) explains \((G^*,\sigma ^*)\). In particular, the connected component \((G^*,\sigma ^*)\) is again an RBMG. \(\square \)
So far, we have shown that every connected component of an n-RBMG is therefore a k-RBMG possibly with a strictly smaller number k of colors. We next ask when the disjoint union of RBMGs is again an RBMG. To this end, we identify certain vertices in the leaf-colored tree \((T,\sigma )\) that, as we shall see below, are related to the decomposition of \(G(T,\sigma )\) into connected components.
Definition 8
Let \((T,\sigma )\) be a leaf-colored tree with leaf set L. An inner vertex u of T is color-complete if \(\sigma (L(T(u)))=\sigma (L)\). Otherwise it is color-deficient.
We will also refer to a subtree \((T(u),\sigma _{|L(T(u))})\) of \((T,\sigma )\) as color-complete if its root is color-complete.
We write A(u) for the set of color-deficient children of u, i.e.,
and set
The 3-RBMG \((G,\sigma )\) on the left hand side can be explained by the tree \((T,\sigma )\) shown on the right. In \((T,\sigma )\), the inner vertex v is a fork. The color-deficient children of v are \(c_1,a_3\) and w, thus \({\mathscr {L}}(v) = \{a_1,b_1,c_1,a_3\}\). Also, \(v'\) is a fork and \({\mathscr {L}}(v') =\{a_2,b_2,c_2\}\). The set of forks is \(\zeta (T,\sigma )=\{v,v'\}\) (color figure online)
Definition 9
Let \((T,\sigma )\) a leaf-colored tree. An inner vertex \(u\in V^0(T)\) is a fork if \(\sigma ({\mathscr {L}}(u))=\sigma (L)\). We write \(\zeta (T,\sigma )\) for the set of forks in T.
For an illustration see Fig. 11. As an immediate consequence of the definition we have
Lemma 11
Every fork in a leaf-colored tree \((T,\sigma )\) is color-complete, but not every color-complete vertex is a fork.
Proof
For a fork u, we have \(\sigma (L)=\sigma (\mathscr {L(T)}(u))\subseteq \bigcup _{v\in \mathsf {child} (u)}\sigma (L(T(v)))=\sigma (L(T(u))\). Thus every fork must be color-complete. In order to see that not every color-complete vertex is a fork, consider a leaf-colored tree \((T,\sigma )\), where \(\rho _T\) has exactly two children both of which are color-complete. Then, \(\rho _T\) is color-complete but \(A(\rho _T)=\emptyset \). Hence, \(\rho _T\) is not a fork. \(\square \)
Clearly, there are no forks in a leaf-labeled tree \((T,\sigma )\) with \(|\sigma (L(T))|=1\). In the following, we will therefore restrict our attention to trees and graphs with at least two colors, omitting the trivial case of 1-RBMGs which correspond to the edge-less graph \((G,\sigma )\) that is explained by any leaf-colored tree \((T,\sigma )\) with leaf set \(L(T) = V(G)\). Next, we derive some useful technical results about forks and color-complete trees, which will be needed to prove the main result of this section.
Lemma 12
Let \((T,\sigma )\) be a leaf-colored tree. Then \(\zeta (T,\sigma )\ne \emptyset \).
Proof
Let \(L=L(T)\). Assume, for contradiction, that \(\zeta (T,\sigma )=\emptyset \). Thus, in particular, \(\rho _T\notin \zeta (T,\sigma )\). Since the root \(\rho _T\) is always color-complete, we have \(\sigma ({\mathscr {L}}(\rho _T))\ne \sigma (L(T(\rho _T)))=\sigma (L)\), which implies \(A(\rho _T) \subsetneq \mathsf {child} (\rho _T)\). Hence, Eq. (12) implies that there is a child \(u_1\) of the root with \(\sigma (L(T(u_1)))=\sigma (L)\). Since \(\zeta (T,\sigma )=\emptyset \), the vertex \(u_1\) is not a fork. Repeating the argument, \(u_1\) must have a child \(u_2\) with \(\sigma (L(T(u_2)))=\sigma (L)\), and so on. Hence, there is a sequence of inner vertices \(\rho _T:=u_0 \succ _T u_1\succ _T u_2\succ _T \dots \succ _T u_k\) such that \(u_j\) has only color-complete children for \(0\le j<k\). Since T is finite, all maximal paths of this form a finite, i.e., the final vertex \(u_k\) in every maximal path has only color-deficient children, i.e., \(A(u)=\mathsf {child} (u)\). Since \(u_k\) itself is color-complete by construction, \(\sigma ({\mathscr {L}}(u))=\sigma (L(T(u)))=\sigma (L)\), i.e., \(u_k\) is fork, a contradiction. \(\square \)
Lemma 13
Let \((G,\sigma )\) be an n-RBMG, \(n\ge 2\), \((T,\sigma )\) a tree with leaf set L that explains \((G,\sigma )\) and \((T(u),\sigma _{|L(T(u))})\) a color-complete subtree of \((T,\sigma )\) for some \(u\in V^0(T)\). Then, \(xy\notin E(G)\) for any two vertices \(x,y\in L\) with \(x\in L(T(u))\) and \(y\in L{\setminus } L(T(u))\).
Proof
If \(u=\rho _T\), then \(L{\setminus } L(T(u)) = \emptyset \) and the lemma is trivially true. Thus suppose \(u\ne \rho _T\). Let \(x\in L(T(u))\) and assume for contradiction \(xy\in E(G)\) for some \(y\in L{\setminus } L(T(u))\), i.e., x and y are reciprocal best matches. By choice of x and y, \({{\,\mathrm{lca}\,}}(x,y)\succ u\) and \(\sigma (x)\ne \sigma (y)\). Since \((T(u),\sigma _{|L(T(u))})\) is color-complete, there exists a leaf \(y'\in L(T(u))\) with \(\sigma (y')=\sigma (y)\). Hence in particular, \(\sigma (y')\ne \sigma (x)\) and thus, \(y'\ne x\). Since \(y'\in L(T(u))\), we have \({{\,\mathrm{lca}\,}}(x,y')\preceq u \prec {{\,\mathrm{lca}\,}}(x,y)\); a contradiction to the assumption that x and y are reciprocal best matches. \(\square \)
Lemma 14
Let \((T,\sigma )\) be a leaf-colored tree with leaf set L that explains the n-RBMG \((G,\sigma )\) with \(n>1\), and let \(u\in \zeta (T,\sigma )\) be a fork in \((T,\sigma )\). Then, the following statements are true:
- (i)
If \(L^*\) is the vertex set of a connected component \((G^*,\sigma ^*)\) of \((G,\sigma )\), then either \(L^*\subseteq {\mathscr {L}}(u)\) or \(L^*\cap {\mathscr {L}}(u)=\emptyset \).
- (ii)
There is a connected component \((G^*,\sigma ^*)\) of \((G,\sigma )\) with leaf set \(L^*\subseteq {\mathscr {L}}(u)\) and \(\sigma (L^*)=\sigma (L)\).
- (iii)
Let \((G^*,\sigma ^*)\) be a connected component of \((G,\sigma )\) with vertex set \(L^*\) and \(\sigma (L^*)=\sigma (L)\). Then, \(u':={{\,\mathrm{lca}\,}}(L^*)\) is a fork and \(L^*\subseteq {\mathscr {L}}(u')\).
Proof
All \(N^+\)-neighborhoods in this proof are taken w.r.t. the underlying BMG \(\vec {G}(T,\sigma )\). By Lemma 12, we have \(\zeta (T,\sigma )\ne \emptyset \) and thus, there exists a fork in \((T,\sigma )\). In what follows, let \(u\in \zeta (T,\sigma )\) be chosen arbitrarily.
(i) Let \((G^*,\sigma ^*)\) be a connected component of \((G,\sigma )\) and \(L^*\) its vertex set. The statement is trivially true if \(|L^*|=1\). Hence, assume that \(|L^*|\ge 2\). By Lemma 11, \((T(u),\sigma _{|L(T(u))})\) is color-complete. Lemma 13 implies \(xy\notin E(G)\) for any pair of leaves \(x\in L(T(u))\) and \(y\in L{\setminus } L(T(u))\). Therefore either \(L^*\subseteq L(T(u))\) or \(L^*\cap L(T(u))=\emptyset \). In the latter case, we have \(L^* \cap {\mathscr {L}}(u)\subseteq L^* \cap L(T(u))=\emptyset \).
Now, suppose \(L^*\subseteq L(T(u))\) and consider a vertex \(x\in L^*\) and let \(z\in L^*{\setminus }\{x\}\) be a neighbor of x, i.e., \(xz\in E(G)\). Such a z exists since \(|L^*|\ge 2\) and \(G^*\) is connected. If \(x\in L(T(u)){\setminus } {\mathscr {L}}(u)\), then there exists a color-complete inner vertex \(v\in \mathsf {child} (u)\) that satisfies \(x\prec v\). Since v is color-complete, Lemma 13 implies that there is no edge between L(T(v)) and \(L(T(u)){\setminus } L(T(v))\) and thus we have \(z\in L(T(v))\). Therefore \(z\notin {\mathscr {L}}(u)\). Now suppose that \(x\in {\mathscr {L}}(u)\). If \(z\notin {\mathscr {L}}(u)\), then \(z\in L(T(u)){\setminus } {\mathscr {L}}(u)\). Thus we can apply analogous arguments and Lemma 13 to conclude that there cannot be an edge between x and z; a contradiction. Hence, \(z\in {\mathscr {L}}(u)\). In summary, we have either \(L^*\subseteq {\mathscr {L}}(u)\) or \(L^*\cap {\mathscr {L}}(u)=\emptyset \).
(ii) Let \(S:=\sigma (L)\) with \(|S|=n>1\). We proceed by induction. For \(n=2\), the statement is a direct consequence of Lemma 10.
For the induction step, suppose the statement is correct for RBMGs with a color set of less than n colors. Recall that for any \(v_i\in A(u)\) the color set of any subtree \((T(v_i),\sigma _{|L(T(v_i))})\) contains less than n colors, i.e., \(S_{v_i}:=\sigma (L(T(v_i))) \ne S\). By Lemma 12, there must exist a fork \(w\in \zeta (T(v_i), \sigma _{|L(T(v_i))})\) within the tree \((T(v_i), \sigma _{|L(T(v_i))})\). Since w is a fork in \((T(v_i), \sigma _{|L(T(v_i))})\), it is therefore also color-complete in \((T(v_i), \sigma _{|L(T(v_i))})\). However, by definition, we have \(w \preceq v_i\in A(u)\) and thus, w is not color-complete in \((T,\sigma )\). Nevertheless, we can apply the induction hypothesis to the RBMG \((G_{v_i},\sigma _{v_i}):=G(T(v_i),\sigma _{|L(T(v_i))})\) to ensure that there exists a connected component \((G^*_{v_i},\sigma ^*_{v_i})\) with leaf set \(L_{v_i}^*\subseteq {\mathscr {L}}(w)\) and \(\sigma (L_{v_i}^*)=S_{v_i}\). Now, fix this index i. By Corollary 1, there is a connected component \((G^*,\sigma ^*)\) with leaf set \(L^*\) of \((G,\sigma )\) that contains \((G^*_{v_i},\sigma ^*_{v_i})\).
Assume, for contradiction, that \(|\sigma (L^*)|<n\). Suppose first that \(|S_{v_i}|=n-1\). Thus, \(S{\setminus } S_{v_i} = \{r\}\) and for each color \(s\in S{\setminus } \{r\}\) there is a vertex \(z\in V(G^*_{v_i})\) with color \(\sigma (z)=s\). By construction, \(u\in \zeta (T,\sigma )\) implies that there exists a vertex \(v_j\in A(u)\) (\(i\ne j\)) such that \(r\in S_{v_j}\). In particular, it follows from Eq. (3) that \(L(T(v_j))\cap L[r] \subseteq N_r^+(x)\) for all \(x\in L(T(v_i))\). Since \(S_{v_i} \subseteq \sigma (L^*)\) but \(|\sigma (L^*)|<n\), we have \(|\sigma (L^*)|=n-1\), and we conclude that \(xy\notin E(G)\) for every \(y\in L(T(v_j))\cap L[r]\) and \(x\in V(G^*_{v_i})\). The latter two arguments imply that \(x\notin N_{\sigma (x)}^+(y)\) for all \(y\in L(T(v_j))\cap L[r]\) and \(x\in V(G^*_{v_i})\). This, however, is only possible if \(L(T(v_j))\) contains leaves of all colors \(s\ne r\), i.e., \(S_{v_i}\subsetneq S_{v_j}\) and thus \(|S_{v_j}|=n\); a contradiction to \(v_j\in A(u)\).
Now, suppose that \(|S_{v_i}|<n-1\), i.e., \(S{\setminus } S_{v_i} = \{r_1,\ldots ,r_m\}\). Again, for any \(r_j\) (\(1\le j \le m\)), there is a vertex \(v_j\in A(u)\) (\(i\ne j\)) such that \(r_j\in S_{v_j}\). Note that \(v_j=v_k\) may be possible for two different colors \(r_j\) and \(r_k\). If there exists a color \(s_j\in S_{v_i}\) that is not contained in \(S_{v_j}\), then, for any \(x\in L(T(v_j))\cap L[r_j]\) and \(y\in L(T(v_i))\cap L[s_j]\), we have \({{\,\mathrm{lca}\,}}_T(x,y)=u\prec _T {{\,\mathrm{lca}\,}}_T(x,y')\) and \({{\,\mathrm{lca}\,}}_T(x,y)=u\prec _T {{\,\mathrm{lca}\,}}_T(x',y)\) for all \(x'\in L[r_j], y'\in L[s_j]\), and hence \(xy\in E(G)\). Thus, there is a connected component in \(G(T(u),\sigma _{|L(T(u))})\) that contains at least all colors \(S_{v_i}\cup \{r_j\}\). Consequently, if for any \(j\in \{1,\dots ,m\}\) there exists such a color \(s_j\in S_{v_i}{\setminus } S_{v_j}\), then there must be a connected component in \(G(T(u),\sigma _{|L(T(u))})\) that contains all colors in S. By Corollary 1, every connected component of \(G(T(u),\sigma _{|L(T(u))})\) is contained in a connected component of \((G,\sigma )\) and statement (ii) is true for this case.
On the other hand, if there is at least one j for which this property is not true, similar argumentation as in the case \(|S_{v_i}|=n-1\) shows that \(S_{v_i}\subset S_{v_j}\), hence in particular \(|S_{v_j}|>|S_{v_i}|\). We can then apply the same argumentation for RBMG \((G_{v_j},\sigma _{v_j}):=G(T(v_j), \sigma _{|L(T(v_j))})\) and either obtain a connected component on n colors in \(G(T(u),\sigma _{|L(T(u))})\) or some inner vertex \(v_k\in A(u)\) with \(|S_{v_i}|<|S_{v_j}|<|S_{v_k}|\). Repeating this argumentation, in each step we either obtain either an n-colored connected component or further increase the sequence \(|S_{v_i}|<|S_{v_j}|<|S_{v_k}|<\cdots \). Since L is finite, this sequence must eventually terminate with \(|S_{v_l}|=n\), contradicting \(v_l\in A(u)\). In summary, we have shown that \(|\sigma (L^*)|\ne n\) is not possible and hence \(\sigma (L^*)=\sigma (L)\). Finally, \(\emptyset \ne L^* \cap L(T(v_i))\) and \(v_i\in A(u)\) implies that \(L^*\cap {\mathscr {L}}(u)\ne \emptyset \). Thus, we can apply Statement (i) to conclude that \(L^*\subseteq {\mathscr {L}}(u)\).
(iii) By Statement (ii), there is a connected component \((G^*,\sigma ^*)\) with vertex set \(L^*\) and \(\sigma (L^*)=\sigma (L)\). Put \(u':={{\,\mathrm{lca}\,}}(L^*)\). We start by showing \(L^*\subseteq {\mathscr {L}}(u')\). Assume, for contradiction, that there exists a leaf \(a\in L^*\) such that \(a\notin {\mathscr {L}}(u')\). Let \(v'\in \mathsf {child} (u')\) be the (unique) child of \(u'\) with \(a\prec _T v'\). Since \(a\notin {\mathscr {L}}(u')\), we can conclude that \(v'\notin A(u')\). Thus \(v'\) is color-complete and therefore, \((T(v'),\sigma _{|L(T(v'))})\) is color-complete. By Lemma 13, we thus have \(b\prec _T v'\) for any \(b\in L\) with \(ab\in E(G)\). Repeating this argument for any \(b\in N(a)\) and \(c\in N(b)\) and so on, this finally implies \(L^*\subseteq _T L(T(v'))\). Therefore \({{\,\mathrm{lca}\,}}(L^*)\preceq _T v'\prec _T u'\); a contradiction to \(u' = {{\,\mathrm{lca}\,}}(L^*)\). Thus we have \(L^*\subseteq {\mathscr {L}}(u')\). As a consequence, \(\sigma ({\mathscr {L}}(u'))=\sigma (L)\), i.e., \(u'\) is a fork. \(\square \)
Corollary 3
Let \((G,\sigma )\) be an n-RBMG, \(n\ge 2\), that is explained by a tree \((T,\sigma )\) with root \(\rho _T\).
- (i)
There exists an n-colored connected component \((G^*,\sigma ^*)\) of \((G,\sigma )\).
- (ii)
If \((G,\sigma )\) is connected, then \(\zeta (T,\sigma )=\{\rho _T\}\).
Proof
(i) Since \(\zeta (T,\sigma )\ne \emptyset \) (see Lemma 12), the existence of an n-colored connected component of \((G,\sigma )\) is a direct consequence of Lemma 14(ii).
(ii) Lemma 14(iii) implies \(\rho _T\in \zeta (T,\sigma )\). By (i) and Lemma 14(ii), we have \(L(T)\subseteq {\mathscr {L}}(u)\subseteq L(T)\) for all \(u\in \zeta (T,\sigma )\), hence \({\mathscr {L}}(u)= L(T)\). Since this is true only if \(u=\rho _T\), assertion (ii) follows. \(\square \)
The following result helps to gain some understanding of the ambiguities among the leaf-colored trees that explain the same RBMG.
Lemma 15
Let \((G,\sigma )\) be an n-RBMG, \(n\ge 2\), explained by \((T,\sigma )\) and \(u\in \zeta (T,\sigma )\) with \(u\ne \rho _T\). Moreover, let \(v\in \mathsf {child} (u)\), where v is color-complete, and \((T',\sigma )\) the tree obtained from \((T,\sigma )\) by replacing the edge uv by \(\mathsf {par} (u)v\). Then, \((T',\sigma )\) explains \((G,\sigma )\).
Proof
First note that, since u is a fork in \((T,\sigma )\), there must exist at least two color-deficient nodes \(w_1, w_2 \in A(u)\). Since v is color-complete, we have \(v\ne w_1,w_2\), thus \(\deg _{T'}(u)>2\), i.e., \((T',\sigma )\) is phylogenetic. In what follows, we show that \((G,\sigma ) = G(T',\sigma )\). Put \(L:=V(G)\).
First, let \(x,y\in L{\setminus } L(T(u))\). Then, by construction of \((T',\sigma )\), we have \({{\,\mathrm{lca}\,}}_T(x,y)={{\,\mathrm{lca}\,}}_{T'}(x,y)\), and \({{\,\mathrm{lca}\,}}_T(x,y)\prec _T z\) implies \({{\,\mathrm{lca}\,}}_{T'}(x,y)\prec _{T'} z\) for all \(z\in V(T)\). In other words, reciprocal best matches xy with \(x,y\notin L(T(u))\) remain reciprocal best matches in \((T',\sigma )\). Moreover, if x and y are not reciprocal best matches in \((T,\sigma )\), then we have w.l.o.g. \({{\,\mathrm{lca}\,}}_T(x,y)\succ _T{{\,\mathrm{lca}\,}}_T(x',y)\) for some (fixed) \(x'\in L[\sigma (x)]\). Clearly, if \(x'\in L{\setminus } L(T(v))\), then we still have, by construction, \({{\,\mathrm{lca}\,}}_{T'}(x,y)={{\,\mathrm{lca}\,}}_T(x,y)\succ _{T'}{{\,\mathrm{lca}\,}}_{T'}(x',y)={{\,\mathrm{lca}\,}}_T(x',y)\). Thus, if \(x'\in L{\setminus } L(T(v))\), then x and y do not form reciprocal best matches in \((T',\sigma )\). If \(x'\in L(T(v))\), then \({{\,\mathrm{lca}\,}}_T(x',y)\succeq _T \mathsf {par} (u)\). Now, \({{\,\mathrm{lca}\,}}_T(x,y)\succ _T{{\,\mathrm{lca}\,}}_T(x',y)\) implies that \({{\,\mathrm{lca}\,}}_T(x,y)\succ _T \mathsf {par} (u)\). In other words, \({{\,\mathrm{lca}\,}}_T(x',y)\) and \({{\,\mathrm{lca}\,}}_T(x,y)\) lie on the path from the root to \(\mathsf {par} (u)\). This and the construction of \((T',\sigma )\) implies that \({{\,\mathrm{lca}\,}}_T(x,y) = {{\,\mathrm{lca}\,}}_{T'}(x,y) \succ _{T'} {{\,\mathrm{lca}\,}}_T(x',y) = {{\,\mathrm{lca}\,}}_{T'}(x',y)\). Thus, x and y do not form reciprocal best matches in \((T',\sigma )\). In summary, \(xy\in E(G)\) if and only if \(xy\in E(G(T,\sigma ))\) for all \(x,y\in L{\setminus } L(T(u))\).
Moreover, since v is color-complete in both trees, we can apply Lemma 13 to conclude that neither \((G,\sigma )\) nor \(G(T',\sigma )\) contains edges between L(T(v)) and \(L{\setminus } L(T(v))\). Since \(T'(v)=T(v)\) by construction, we additionally have \(G(T'(v),\sigma _{|L(T(v))})=G(T(v),\sigma _{|L(T(v))})= (G[L(T(v))],\sigma _{|L(T(v))})\).
It remains to show the case \(x\in L':=L(T(u)){\setminus } L(T(v))\), and either \(y\in L'\) or \(y \in L{\setminus } L(T(u))\). Suppose first that \(y \in L{\setminus } L(T(u))\). Since u is a fork, Lemma 14(ii) implies that there exists a connected component \((G^*,\sigma ^*)\) of \((G,\sigma )\) with leaf set \(L^*\) such that \(L^*\subseteq {\mathscr {L}}(u)\). In particular, as v is color-complete, it is not contained in A(u). We therefore conclude that \(L^*\subseteq L'\), i.e., the subtree \((T_{|L'},\sigma _{|L'})\) is color-complete as well. Since by construction \(T'(u)=T(u){\setminus } T(v)\), Lemma 13 implies that there are no edges between L(T(u)) and \(L{\setminus } L(T(u))\) in both \((G,\sigma )\) and \(G(T',\sigma )\). In other words, x and y do not form reciprocal best matches, neither in \((T,\sigma )\) nor in \((T',\sigma )\) whenever \(x\in L':=L(T(u)){\setminus } L(T(v))\) and \(y \in L{\setminus } L(T(u))\).
Now, suppose that \(y\in L'\). If x and y do not form reciprocal best matches in \((T,\sigma )\), then we have w.l.o.g. \({{\,\mathrm{lca}\,}}_T(x,y)\succ _T{{\,\mathrm{lca}\,}}_T(x',y)\) for some (fixed) \(x'\in L[\sigma (x)]\). This immediately implies that \(x'\in L'\). Again, since \(T'(u)=T_{|L'}\), we have \({{\,\mathrm{lca}\,}}_T(x,y)={{\,\mathrm{lca}\,}}_{T'}(x,y)\succ _{T'} {{\,\mathrm{lca}\,}}_T(x',y) = {{\,\mathrm{lca}\,}}_{T'}(x',y)\). Hence, x and y do not form reciprocal best matches in x and y in \((T',\sigma )\). Finally, if x and y are reciprocal best matches in \((T,\sigma )\), then \({{\,\mathrm{lca}\,}}_T(x,y) \preceq _T {{\,\mathrm{lca}\,}}_T(x',y)\) and \({{\,\mathrm{lca}\,}}_T(x,y) \preceq _T {{\,\mathrm{lca}\,}}_T(x,y')\) for all \(x'\in L[\sigma (x)]\) and \(y'\in L[\sigma (y)]\). We first fix a leaf \(x'\in L[\sigma (x)]\) for which the latter inequality is satisfied. By construction, \( {{\,\mathrm{lca}\,}}_{T}(x,y) = {{\,\mathrm{lca}\,}}_{T'}(x,y) \preceq _{T'} u\). Clearly, if \(x'\in L'\), then the fact \(T'(u)=T_{|L'}\) implies that \({{\,\mathrm{lca}\,}}_{T'}(x,y) \preceq _{T'} {{\,\mathrm{lca}\,}}_{T'}(x',y)\). On the other hand, if \(x'\notin L'\), then \({{\,\mathrm{lca}\,}}_{T'}(x',y)\succ _{T'} u\) by construction of \((T',\sigma )\). We thus have \({{\,\mathrm{lca}\,}}_{T'}(x,y) \preceq _{T'} u \prec _{T'} {{\,\mathrm{lca}\,}}_{T'}(x',y)\). Hence, \({{\,\mathrm{lca}\,}}_T(x,y) \preceq _T {{\,\mathrm{lca}\,}}_T(x',y)\) implies \({{\,\mathrm{lca}\,}}_{T'}(x,y) \preceq _{T'} {{\,\mathrm{lca}\,}}_{T'}(x',y)\) for all \(x'\in L[\sigma (x)]\). Analogous arguments hold for \(y'\in L[\sigma (y)]\). Hence, x and y remain reciprocal best matches in \((T',\sigma )\).
In summary, \(xy\in E(G)\) if and only \(xy\in E(G(T',\sigma ))\). \(\square \)
Let \((G,\sigma )\) be an undirected, vertex colored graph with vertex set L and \(|\sigma (L)|=n\). We denote the connected components of \((G,\sigma )\) by \((G_i^n,\sigma _i^n)\), \(1\le i \le k\), with vertex sets \(L_i^n\) if \(\sigma (L_i^n)=\sigma (L)\) and \((G_j^{<n},\sigma _j^{<n})\), \(1\le j \le l\), with vertex sets \(L_j^{<n}\) if \(\sigma (L_j^{<n})\subsetneq \sigma (L)\). That is, the upper index distinguishes components with all colors present from those that contain only a proper subset. Suppose that each \((G_i^n,\sigma _i^n)\) and \((G_j^{<n},\sigma _j^{<n})\) is an RBMG. Then there are trees \((T_i^n,\sigma _i^n)\) and \((T_j^{<n},\sigma _j^{<n})\) explaining \((G_i^n,\sigma _i^n)\) and \((G_j^{<n},\sigma _j^{<n})\), respectively. The roots of these trees are \(u_i\) and \(v_j\), respectively. We construct a tree \((T_G^*,\sigma )\) with leaf set L in two steps:
- (1)
Let \((T',\sigma ^n)\) be the tree obtained by attaching the trees \((T_i^n,\sigma _i^n)\) with their roots \(u_i\) to a common root \(\rho '\).
- (2)
First, construct a path \(P=v_1v_2\dots v_{l-1}v_l\rho '\), where \(\rho '\) is omitted whenever \(T'\) is empty. Now attach the trees \((T_j^{<n},\sigma _j^{<n})\), \(1\le j\le l\), to P by identifying the root of each \(T_j^{<n}\) with the vertex \(v_j\) in P. Finally, if \((T',\sigma ^n)\) exists, attach it to P by identifying the root of \(T'\) with the vertex \(\rho '\) in P. The coloring of L is the one given for \((G,\sigma )\).
This construction is illustrated in Fig. 4 for \(n\ge 2\). For \(n=1\), the resulting tree is simply the star tree on L.
Our goal for the remainder of this section is to show that every RBMG is explained by a tree of the form \((T_G^*,\sigma )\). We start by collecting some useful properties of \((T_G^*,\sigma )\).
Observation 2
Let \((G,\sigma )\) be an undirected vertex colored graph with \(|\sigma (V(G))|\ge 2\) whose connected components are RBMGs and let \((T_G^*,\sigma )\) be the tree described above. Then
- (i)
\(\zeta (T^*_G,\sigma )=\{u_1,\dots ,u_k\}\),
- (ii)
Every subtree \((T_i^n,\sigma _i^n)\), \(1\le i\le k\) and \((T^*(v_j),\sigma _{|L(T_G^*(v_j))})\) and \(1\le j\le l\), resp., is color-complete.
Proof
Statement (i) is an immediate consequence of Corollary 3(ii). For Statement (ii) observe that, by construction, \(\sigma (L^n_i) = \sigma (L)\) and thus, \((T_i^n,\sigma _i^n)\) is a color-complete subtree of \((T^*_G,\sigma )\), \(1\le i\le k\). By step (2) of the construction of \((T^*_G,\sigma )\), we have \(u_1\prec _{T_G^*}\rho '\prec _{T_G^*} v_l\prec _{T_G^*}\cdots \prec _{T_G^*} v_1\). Since \(u_1\) is color-complete by assumption, so is each of its ancestors. \(\square \)
Lemma 16
Let \((G,\sigma )\) be an undirected vertex colored graph on n colors whose connected components are RBMGs and there is at least one n-colored connected component, and let \((T^*_G,\sigma )\) be the tree described above. Then \((T^*_G,\sigma )\) explains \((G,\sigma )\).
Proof
For \(n=1\), \((T^*_G,\sigma )\) is simply the star tree on V(G). Clearly, \((G,\sigma )\) must be the edge-less graph, which is explained by \((T^*_G,\sigma )\). Now suppose \(n>1\). Let \((G^n_i,\sigma ^n_i)\) be an n-colored connected component of \((G,\sigma )\), \(i\in \{1,\dots ,k\}\) and \(k\ge 1\). It has vertex set \(L_i^{n}=L(T^*_G(u_i))\). By construction, \((T^*_G(u_i), \sigma _{|L_i^{n}}) = (T_i^n,\sigma _i^n)\) explains \((G^n_i,\sigma ^n_i)\) and \((G[L_i^n],\sigma _{|L_i^n}) = (G^n_i,\sigma ^n_i)\). Moreover, \((T^*_G(u_i), \sigma ^n_i)\) is a color-complete subtree of \((T^*_G,\sigma )\) that is rooted at \(u_i\). Hence, Lemma 13 implies that there are no edges in \(G(T^*_G,\sigma )\) between \(L_i^{n}\) and any other vertex in \(L{\setminus } L_i^{n}\). In other words, \((G^n_i,\sigma ^n_i)\) remains a connected component in \(G(T^*_G,\sigma )\), \(i\in \{1,\dots ,k\}\).
Now, suppose that there is a connected component \((G^{<n}_j,\sigma ^{<n}_j)\), \(j\in \{1,\dots ,l\}\) and \(l\ge 1\), which contains less than n colors. Again, by construction, \((T^*_G(v_j)_{|L_j^{<n}}, \sigma _{|L_j^{<n}}) = (T_j^{<n},\sigma _j^{<n})\) explains \((G^{<n}_j,\sigma ^{<n}_j)\) and \((G[L_i^{<n}],\sigma _{|L_i^{<n}})= (G^{<n}_j,\sigma ^{<n}_j)\). Furthermore, we have \(L^{<n}_{j'}\cap L(T^*_G(v_j))=\emptyset \) if and only if \(j'<j\) by construction of the path \(v_1v_2\dots v_l\) in \(T^*_G\). By Observation 2(ii), \(v_j\) is color-complete and Lemma 13 implies that there is no edge between \(L^{<n}_{j}\) and any \(L^{<n}_{j'}\) whenever \(j'<j\). In other words, \((G^{<n}_j,\sigma ^{<n}_j)\), \(j\in \{1,\dots ,l\}\) remains a connected component in \(G(T^*_G,\sigma )\).
To summarize, all connected components of \((G,\sigma )\) remain connected components in \(G(T^*_G,\sigma )\) and are explained by restricting \((T^*_G,\sigma )\) to the corresponding leaf set, which completes the proof. \(\square \)
Theorem 3
An undirected leaf-colored graph \((G,\sigma )\) is an RBMG if and only if each of its connected components is an RBMG and at least one connected component contains all colors.
Proof
For \(n=1\), the statement trivially follows from the fact that an RBMG must be properly colored and thus, a 1-RBMG must be the edge-less graph. Now suppose \(n>1\). By Theorem 2 every connected component of an RBMG is again an RBMG. Corollary 3(i) ensures the existence of a connected component containing all colors. Conversely, if \((G,\sigma )\) is an undirected graph whose connected components are RBMGs and at least one of them contains all colors, then Lemma 16 guarantees that it is explained by a tree of the form \((T^*_G,\sigma )\), and hence it is an RBMG. \(\square \)
Corollary 4
Every RBMG can be explained by a tree of the form \((T^*_G,\sigma )\).
Three classes of connected 3-RBMGs
1.1 Three special classes of trees
We start with a rather technical result that allows us to simplify the structure of trees explaining a given 3-RBMG.
Lemma 17
Let \((G,\sigma )\) be an \({\mathsf {S} }\)-thin 3-RBMG that is explained by \((T,\sigma )\). Moreover, let \(u\in V^0(T)\) be a vertex that has two distinct children \(v_1,v_2\in \mathsf {child} (u)\) such that \(\sigma (L(T(v_1)))=\sigma (L(T(v_2)))\subsetneq \sigma (L(T))\) and \(v_1\in V^0(T)\), and denote by \((T',\sigma )\) the tree obtained by replacing the edge \(uv_2\) in \((T,\sigma )\) by \(v_1v_2\) and possible suppression of u, in case u has exactly two children in \((T,\sigma )\) or removal of u and its incident edge, in case \(u=\rho _{T'}\). Then \((T',\sigma )\) explains \((G,\sigma )\).
Proof
It is easy to see that the resulting tree \((T',\sigma )\) is phylogenetic. We emphasize that this proof does not depend on whether u has been suppressed or removed. Put \(L:=L(T)\). Moreover, Lemma 8 implies that \(L(T(v_1))\) contains leaves of more than one color, hence \(|\sigma (L(T(v_1)))|=2\).
Let \(S=\{r,s,t\}\) be the color set of \((G,\sigma )\) and \(\sigma (L(T(v_1)))=\{r,s\}\). Since \(L(T(v_1))\) and \(L(T(v_2))\) do not contain leaves of color t, we have \({{\,\mathrm{lca}\,}}_T(y,z)={{\,\mathrm{lca}\,}}_{T'}(y,z)\succeq u\) for every \(y\in L[r]\cup L[s]\) and \(z\in L[t]\). Hence, \(yz \in E(G)\) if and only if \(yz\in E(G(T',\sigma ))\) for every \(y\in L[r]\cup L[s]\) and \(z\in L[t]\). It therefore suffices to consider \((T_{rs},\sigma _{rs}):=(T_{|L[r]\cup L[s]},\sigma _{|L[r]\cup L[s]})\) and \((T'_{rs},\sigma _{rs}):=(T'_{|L[r]\cup L[s]},\sigma _{|L[r]\cup L[s]})\).
First note that, since \(T'(v_2)=T(v_2)\), vertex \(v_2\) is color-complete in both \((T_{rs},\sigma _{rs})\) and \((T'_{rs},\sigma _{rs})\). Hence, Lemma 13 implies that neither \(G(T_{rs},\sigma _{rs})\) nor \(G(T'_{rs},\sigma _{rs})\) contains edges of the form xy, where \(x\in L(T(v_2))\) and \(y\notin L(T(v_2))\). Moreover, since \(T'(v_2)=T(v_2)\), we have \(G(T_{rs}(v_2),\sigma _{|L(T(v_2))})=G(T'_{rs}(v_2),\sigma _{|L(T(v_2))})\). Since \(v_1\) is also color-complete in \((T_{rs},\sigma _{rs})\) and \((T'_{rs},\sigma _{rs})\), we can similarly conclude that both graphs \(G(T_{rs},\sigma _{rs})\) and \(G(T'_{rs},\sigma _{rs})\) contain no edges xy, where \(x\in L(T(v_1))\) and \(y\notin L(T(v_1))\). Hence, it suffices to consider edges between leaves in \(L(T(v_1))\) If \(v_1\) is a fork in \((T_{rs},\sigma _{rs})\), one can easily see that \((T,\sigma )\) is obtained from \((T',\sigma )\) by the same operation used in Lemma 15. Hence, Lemma 15 implies that \(G(T_{rs},\sigma _{rs})=(G[L[r]\cup L[s]],\sigma _{rs})\). Suppose that \(v_1\) is not a fork. Note that any \(w\in \mathsf {child} _T(v_1)\) with \(|\sigma (L(T(w)))|=1\) must be a leaf as, otherwise, all leaves in L(T(w)) would be in a common \({\mathsf {S} }\)-class and \((G,\sigma )\) would not be \({\mathsf {S} }\)-thin. Therefore, any \(w\in \mathsf {child} _T(v_1)\) is either color-complete or a leaf in \((T_{rs},\sigma _{rs})\). Therefore, by Lemma 13, there are no edges between \(G(T_{rs}(w_1),\sigma _{|L(T(w_1))})\) and \(G(T_{rs}(w_2),\sigma _{|L(T(w_2))})\) as soon as one of the children \(w_1\) and \(w_2\) is a non-leaf vertex. In other words, if there are edges between \(G(T_{rs}(w_1),\sigma _{|L(T(w_1))})\) and \(G(T_{rs}(w_2),\sigma _{| L(T(w_2))})\), then both vertices \(w_1,w_2\in \mathsf {child} _T(v_1)\) are also contained in L. Since, by construction, \(\mathsf {child} _T(v_1)\cap L=\mathsf {child} _{T'}(v_1)\cap L\), we have \(w_1w_2\in E(G(T_{rs},\sigma _{rs}))\) if and only if \(w_1w_2\in E(G(T'_{rs},\sigma _{rs}))\) for any \(w_1,w_2\in \mathsf {child} _T(v_1)\). Moreover, by construction, we have \((T(w),\sigma _{|L(T(w))})=(T'(w),\sigma _{|L(T(w))})\) for any inner vertex \(w\in \mathsf {child} _T(v_1)\), hence \(G(T(w),\sigma _{|L(T(w))})=G(T'(w),\sigma _{|L(T(w))})\), which concludes the proof. \(\square \)
Definition 10
(Harary and Schwenk 1973) A rooted tree T is a caterpillar if every inner vertex has a most one child that is an inner vertex.
Assume that the tree \((T',\sigma )\) is the 2-colored restricted version of some tree that explains a 3-RBMG. It is easy to verify that all three trees \((T',\sigma )\), \((T'',\sigma )\), and \((T,\sigma )\) explain the same 2-RBMG \((G,\sigma )\). According to the transformation of Lemma 17, \((T'',\sigma )\) is obtained from \((T',\sigma )\) by deletion of the edge \(uv_2\), inserting \(v_1v_2\) and removal of u and its single incident edge. Similarly, \((T,\sigma )\) is obtained from \((T'',\sigma )\) by deleting \(v_1v_2\) and inserting \(v_3v_2\). The final tree \((T,\sigma )\) is a caterpillar (color figure online)
Repeated application of the transformation as in Lemma 17 implies the following result, which is illustrated in Fig. 12.
Corollary 5
Let \((G,\sigma )\) be an \({\mathsf {S} }\)-thin 3-RBMG. Then there exists a tree \((T,\sigma )\) explaining \((G,\sigma )\) for which every 2-colored subtree \((T(u),\sigma _{|L(T(u))})\) with \(|\sigma (L(T(u)))|=2\) is a caterpillar and \(\sigma (L(T(v_1)))\ne \sigma (L(T(v_2)))\) for any distinct \(v_1,v_2\in \mathsf {child} (u)\).
Proof
Let \((T',\sigma )\) explain \((G,\sigma )\) and let \(u\in V^0(T')\) be such that \((T'(u),\sigma _{|L(T'(u))})\) is a 2-colored subtree of \((T',\sigma )\). Suppose there exists an inner vertex \(v\in V^0(T'(u))\) with two distinct children that are again inner vertices, i.e., \(w_1,w_2\in \mathsf {child} (v)\cap V^0(T'(u))\). Since \((G,\sigma )\) is \({\mathsf {S} }\)-thin, we can apply Lemma 8 to conclude that \((T'(w_1),\sigma _{|L(T'(w_1))})\) and \((T'(w_2),\sigma _{|L(T'(w_2))})\) are both 2-colored subtrees, thus \(\sigma (L(T'(w_1)))=\sigma (L(T'(w_2)))\subsetneq \sigma (L)\). By Lemma 17, the tree \((T'',\sigma )\) that is obtained from \((T',\sigma )\) by deleting \(vw_2\) and inserting \(w_1w_2\), still explains \((G,\sigma )\) and satisfies \(|\mathsf {child} (v)\cap V^0(T''(u))|=|\mathsf {child} (v)\cap V^0(T'(u))|-1\). Repeating this transformation until each inner vertex \(v\in V^0(T)\) satisfies \(\sigma (L(T(v_1)))\ne \sigma (L(T(v_2)))\) for any \(v_1,v_2\in \mathsf {child} _T(v)\), finally yields a tree \((T,\sigma )\) for which \(|\mathsf {child} (v)\cap V^0(T(u))|\le 1\), i.e., a caterpillar, that explains \((G,\sigma )\). In particular, we have \(|\sigma (L(T(v_1)))|=1\) if and only if \(v_1\in L\) (cf. Lemma 8), and v cannot have two leaves of the same color as children because \((G,\sigma )\) is \({\mathsf {S} }\)-thin. \(\square \)
The restriction to connected \({\mathsf {S} }\)-thin graphs with 3 colors together with the fact that all 2-colored subtrees can be chosen to be caterpillars according to Corollary 5 identifies three distinct classes of trees, see Fig. 6.
Definition 11
Let \((T,\sigma )\) be a 3-colored tree with color set \(S=\{r,s,t\}\). The tree \((T,\sigma )\) is of
- Type (I),:
if there exists \(v\in \mathsf {child} (\rho _T)\) such that \(|\sigma (L(T(v)))|=2\) and \(\mathsf {child} (\rho _T){\setminus } \{v\}\subsetneq L\).
- Type (II),:
if there exists \(v_1, v_2\in \mathsf {child} (\rho _T)\) such that \(|\sigma (L(T(v_1)))|=|\sigma (L(T(v_2)))| = 2\), \(\sigma (L(T(v_1)))\ne \sigma (L(T(v_2)))\) and \(\mathsf {child} (\rho _T){\setminus } \{v_1,v_2\}\subsetneq L\),
- Type (III),:
if there exists \(v_1, v_2, v_3\in \mathsf {child} (\rho _T)\) such that \(\sigma (L(T(v_1)))=\{r,s\}\), \(\sigma (L(T(v_2)))=\{r,t\}\), \(\sigma (L(T(v_3)))=\{s,t\}\), and \(\mathsf {child} (\rho _T){\setminus } \{v_1,v_2, v_3\} \subsetneq L\).
Lemma 18
Let \((G,\sigma )\) be an \({\mathsf {S} }\)-thin connected 3-RBMG with vertex set L and color set \(\sigma (L)=\{r,s,t\}\). Then, there is a tree \((T,\sigma )\) with root \(\rho _T\) explaining \((G,\sigma )\) that satisfies the properties in Corollary 5 and is of Type (I), (II) or (III). In particular, all leaves that are incident to the root of \((T,\sigma )\) must have pairwise distinct colors.
Proof
Since \((G,\sigma )\) is an RBMG, there is a tree \((T,\sigma )\) that explains \((G,\sigma )\). Denote its root by \(\rho _{T}\). Note, \(|\sigma (L)|=3\) implies that \(|L|\ge 3\).
If \(|L|=3\), then it is easy to see that G must be a complete graph on three vertices. In this case, any tree \((T,\sigma )\) where T is a triple explains \((G,\sigma )\) and satisfies Type (I) and Corollary 5.
Now suppose that \(|L|>3\). Since \((G,\sigma )\) is connected, Corollary 3(ii) implies that \(\zeta (T,\sigma )=\{\rho _{T}\}\). Lemma 14(i) then implies \(L\subseteq {\mathscr {L}}(\rho _T) \subseteq L\), i.e., \(A(\rho _{T})=\mathsf {child} (\rho _{T})\), and thus \(|\sigma (L(T(v)))|<3\) for every \(v\in \mathsf {child} (\rho _{T})\). This is, every proper subtree of \((T,\sigma )\) contains at most two colors. As a consequence of Corollary 5, the tree \((T,\sigma )\) can be chosen such that there is no pair of distinct vertices \(v_1,v_2\in \mathsf {child} (\rho _{T})\) for which \(\sigma (L(T(v_1)))=\sigma (L(T(v_2)))\). Moreover, as \(|L|>3\) and \(|\sigma (L)|=3\), it follows directly from Corollary 5 that \(|\sigma (L(T(v)))| =1\) for every child \(v\in \mathsf {child} (\rho _T)\) is not possible. Thus, there is at least one child \(v\in \mathsf {child} (\rho _T)\) with \(|\sigma (L(T(v)))|\ne 1\) and thus, \(|\sigma (L(T(v)))| =2\).
In summary, there are only six possible subtrees \((T(v),\sigma _{L(T(v))})\) with \(v\in \mathsf {child} (\rho _{T})\), three containing two colors and three containing only a single color, and each of these six types of subtrees can appear at most once, while there is, in addition, at least one child \(v\in \mathsf {child} (\rho _{T})\) where \((T(v),\sigma _{L(T(v))})\) contains two colors.
Therefore, we end up with the three cases (I), (II), and (III): If there is exactly one vertex \(v\in \mathsf {child} (\rho _T)\) such that the subtree \((T(v),\sigma _{L(T(v))})\) contains two colors, any other leaf in \(L{\setminus } L(T(v))\) must be directly attached to \(\rho _T\), thus Condition (I) is satisfied. Similarly, Condition (II) and (III), respectively, correspond to the case where there exist two and three 2-colored subtrees below the root. Since the three types of trees (I), (II), and (III) differ by the number of two-colored subtrees of the root, no tree can belong to more than one type. By the choice of \((T,\sigma )\), it satisfies Corollary 5.
Finally, if the root of a tree is incident to two leaves of the same color, then the graph explained by this tree cannot be \({\mathsf {S} }\)-thin. Thus, the last statement must be satisfied. \(\square \)
The fact that every connected 3-RBMG can be explained by a tree with a very peculiar structure can now be used to infer stringent structural constraints on the 3-RBMGs themselves.
Lemma 19
Let \((G,\sigma )\) be an \({\mathsf {S} }\)-thin connected 3-RBMG with vertex set L, \(\sigma (L)=\{r,s,t\}\) and \((T,\sigma )\) be a tree of Type (I), (II), or (III) explaining \((G,\sigma )\). Consider \(v\in \mathsf {child} (\rho _T)\) such that \(\sigma (L(T(v))) = \{r,s\}\). Then:
- (i)
If \(x\in L(T(v)) \cap L[r]\), then \(xy\in E(G)\) for \(\sigma (y)=s\) if and only if \(\mathsf {par} (x)=\mathsf {par} (y)\) and thus, \(y\in L(T(v))\).
If, in addition, there is a vertex \(w\in \mathsf {child} (\rho _T){\setminus } \{v\}\) with \(\sigma (L(T(w)))=\{r,t\}\), i.e., \((T,\sigma )\) is of either Type (II) or (III), then the following statements hold:
- (ii)
For any \(y\in L(T(v))\), \(z\in L(T(w))\), we have \(yz\in E(G)\) if and only if \(y\in L[s]\) and \(z\in L[t]\).
- (iii)
If \((T,\sigma )\) is of Type (II), then \(yz\in E(G)\) for every \(y\in L[s]\) and \(z\in L[t]\).
- (iv)
For any \(a\in L(T(v))\), \(b\in \mathsf {child} (\rho _T)\cap L\) with \(\sigma (b)\ne \sigma (a)\), we have \(ab\in E(G)\) if and only if \(\sigma (b)\notin \sigma (L(T(v)))\).
Proof
(i) We assume \(y\in L[s]\) and \(xy\in E(G)\). For contradiction, suppose \(y\notin L(T(v))\). Since L(T(v)) contains at least one leaf \(y'\ne y\) of color s, we have \({{\,\mathrm{lca}\,}}(x,y')\preceq v \prec {{\,\mathrm{lca}\,}}(x,y)\), which implies \(xy\notin E(G)\); the desired contradiction. Hence, \(y\in L(T(v))\). Now assume, again for contradiction, \(\mathsf {par} (x)\ne \mathsf {par} (y)\). There are three cases: (a) \(\mathsf {par} (x)\) and \(\mathsf {par} (y)\) are incomparable in \((T,\sigma )\), (b) \(\mathsf {par} (x)\prec _T\mathsf {par} (y)\), or (c) \(\mathsf {par} (y)\prec _T\mathsf {par} (x)\). In Case (a), Lemma 8 implies that there is a leaf \(y'\in L(T(\mathsf {par} (x))\cap L[s]\) and therefore, \({{\,\mathrm{lca}\,}}(x,y')\prec {{\,\mathrm{lca}\,}}(x,y)\); again a contradiction to \(xy\in E(G)\). Similar argumentation can be applied to the Cases (b) and (c). Hence, we conclude that \(\mathsf {par} (x)=\mathsf {par} (y)\).
Conversely, assume \(\mathsf {par} (x)=\mathsf {par} (y)\) and \(y\in L(T(v))\). By construction, we have \(\mathsf {par} (x)={{\,\mathrm{lca}\,}}(x,y)\preceq {{\,\mathrm{lca}\,}}(x,y')\) for all \(y'\in L[s]\), thus \(xy\in E(G)\).
(ii) Let \(y\in L(T(v))\), \(z\in L(T(w))\) and \(yz\in E(G)\). Assume, for contradiction, \(\sigma (y)=r\). Since \((G,\sigma )\) does not contain edges between vertices of the same color, we have \(z\in L[t]\). By construction of \((T,\sigma )\), there must be some \(x\in L(T(w))\) of color r. Hence, \({{\,\mathrm{lca}\,}}(z,x)\preceq w \prec {{\,\mathrm{lca}\,}}(z,y)=\rho _T\); a contradiction to \(yz\in E(G)\). Thus, \(\sigma (y)=s\). An analogous argument yields \(\sigma (z)=t\). Conversely, let \(y\in L(T(v))\) and \(z\in L(T(w))\) such that \(\sigma (y)=s\) and \(\sigma (z)=t\). Since neither \(t\in \sigma (L(T(v)))\) nor \(s\in \sigma (L(T(w)))\) and \((T,\sigma )\) is of Type (II) or (III), we can immediately conclude that \({{\,\mathrm{lca}\,}}(y,z)=\rho _T = {{\,\mathrm{lca}\,}}(y,z')={{\,\mathrm{lca}\,}}(y',z)\) for all \(y'\in L[s]\) and all \(z'\in L[t]\). Thus, \(yz\in E(G)\).
(iii) Since, \(s\notin \sigma (L(T(w)))\), \(t\notin \sigma (L(T(v)))\), and \((T,\sigma )\) is of Type (II), we have \({{\,\mathrm{lca}\,}}_T(y,z)=\rho _T\) for any pair \(y\in L[s]\), \(z\in L[t]\). Thus, \(yz\in E(G)\).
(iv) Let \(\sigma (a)=r\) and suppose first \(\sigma (b)=s\). Then, there is some \(y\prec v\) with \(\sigma (y)=s\), thus \({{\,\mathrm{lca}\,}}(a,y)\prec {{\,\mathrm{lca}\,}}(a,b)\). Therefore a and b cannot be reciprocal best matches, i.e., \(ab\notin E(G)\). Now assume \(\sigma (b)=t\). Since \(t\notin \sigma (L(T(v)))\), we have \({{\,\mathrm{lca}\,}}(a,z)=\rho _T\) for every \(z\in L[t]\). In particular, we have \({{\,\mathrm{lca}\,}}(b, L[r])=\rho _T\), and therefore \(ab\in E(G)\). \(\square \)
We note in passing that Lemma 19(iv) is also satisfied by Type (I) trees.
In the following we also need a special form of Type (II) trees:
Definition 12
A tree \((T,\sigma )\) of Type (II) with color set \(S=\{r,s_1,s_2\}\) and root \(\rho _T\), where \(v_1,v_2\in \mathsf {child} (\rho _T)\) with \(\sigma (L(T(v_1)))=\{r,s_1\}\) and \(\sigma (L(T(v_2)))=\{r,s_2\}\), is of Type (II\(^*\)) if, for \(i\in \{1,2\}\), it satisfies:
- (\(\star \)):
If there is a vertex \(w\in V^0(T(v_i))\) such that \(\mathsf {child} (w) \cap L=\{x\}\) for some \(x\in L[r]\), then there is a vertex \(v\in \mathsf {child} (\rho _T)\) such that \(\sigma (v)=s_i\).
For leaf-colored trees explaining an \({\mathsf {S} }\)-thin graph, Definition 12 implies, in particular, that if there is some vertex \(w\in V^0(T(v_i))\) with \(\sigma (\mathsf {child} (w) \cap L)=\{r\}\) in a tree \((T,\sigma )\) of Type (II\(^*\)), then \( L[s_i]{\setminus } L(T(v_i))\ne \emptyset \). Moreover, note that in a leaf-colored tree explaining an \({\mathsf {S} }\)-thin graph, the property \(\sigma (\mathsf {child} (w) \cap L)=\{r\}\) always implies \(|\mathsf {child} (w) \cap L|=1\).
Given an arbitrary tree \((T,\sigma )\) of Type (II) with colors and subtrees as in Definition 12, one can easily construct a corresponding tree \((T',\sigma )\) of Type (II\(^*\)) using the following rule for \(i\in \{1,2\}\):
- (r)
If there is no vertex \(v\in \mathsf {child} (\rho _T)\) such that \(\sigma (v)=s_i\), then re-attach all vertices \(x\in L[r]\) with \(\mathsf {child} (\mathsf {par} (x))\cap L =\{x\}\) to \(\rho _T\) and suppress \(\mathsf {par} (x)\) in case \(\mathsf {par} (x)\) has degree 2 after removal of the edge \(\mathsf {par} (x)x\).
By construction, the tree \((T',\sigma )\) has no vertices \(w\in V^0(T(v_i))\) with \(\sigma (\mathsf {child} (w) \cap L)=\{r\}\), and thus, \((T',\sigma )\) trivially satisfies (\(\star \)). Hence, \((T',\sigma )\) is of Type (II\(^*\)).
We proceed by showing that rule (r) must be applied to at most one leaf in order to obtain a tree \((T',\sigma )\) of Type (II\(^*\)).
Lemma 20
Let \((T,\sigma )\) be Type (II) tree that is not of Type (II\(^*\)) and that explains a connected \({\mathsf {S} }\)-thin 3-RBMG. Let \(\rho _T\) be the root of \((T,\sigma )\) and \(S=\{r,s_1,s_2\}\) its color set. Moreover, let \(v_1,v_2\in \mathsf {child} (\rho _T)\) such that \(\sigma (L(T(v_i)))=\{r,s_i\}\), \(i\in \{1,2\}\). Then,
- (i)
no leaf of color r is incident to \(\rho _T\) and
- (ii)
if Rule (r) is applied to some vertex \(x\in L(T(v_i))\), then x is the only leaf in \(L[r]\cap L(T(v_i))\) with \(\mathsf {child} (\mathsf {par} (x))\cap L =\{x\}\) and all inner vertices in \(L(T(v_j))\), \(j\ne i\) satisfy Property (\(\star \)) in Definition 12.
Proof
First note that, since \((T,\sigma )\) is of Type (II), it satisfies \(\mathsf {child} (\rho _T){\setminus } \{v_1,v_2\}\subset L\). Since \((T,\sigma )\) is not of Type (II\(^*\)), there must be a leaf \(x\in L[r]\) with \(w:=\mathsf {par} (x)\preceq _T v_i\) and \(\sigma (\mathsf {child} (w)\cap L)=\{r\}\) such that there is no leaf of color \(s_i\) incident to \(\rho _T\), i.e., \(L[s_i]\subseteq L(T(v_i))\) for some \(i\in \{1,2\}\). W.l.o.g. we can assume \(i=1\). Now, \(L[s_1]\subseteq L(T(v_1))\) and Lemma 19(i) implies that \(N_{s_1}(x)=\emptyset \) in \((G,\sigma )\). However, since \((G,\sigma )\) is connected, there must exist some \(z\in L[s_2]\) such that \(xz\in E(G)\). Lemma 19(i)+(iv) then implies that every \(z\in L[s_2]\) with \(xz\in E(G)\) must be incident to \(\rho _T\). However, Lemma 18 implies that z is the only leaf of color \(s_2\) that is incident to the root. Since \(N_{s_1}(x)=\emptyset \), it holds that z is the only vertex in L that is adjacent to x in G and thus, \(N(x)=\{z\}\) in \((G,\sigma )\).
In order to show Statement (i), we now assume for contradiction that there exists another leaf \(x'\ne x\) of color r such that \(x'\in \mathsf {child} (\rho _T)\). Then, as a consequence of Lemma 18 and since \(L[s_1]\subseteq L(T(v_1))\), we have \(\mathsf {child} (\rho _T)\cap L=\{x',z\}\). Thus Lemma 19(i)+(iv) implies that \(x'\) is not adjacent to any vertex in \(L(T(v_1))\cup L(T(v_2))\). Moreover, we have \({{\,\mathrm{lca}\,}}_T(x',z) = \rho _T = {{\,\mathrm{lca}\,}}_T(x'',z) ={{\,\mathrm{lca}\,}}_T(x',z')\) for all \(x''\in L[r]\) and \(z'\in L[s_2]\), hence \(x'z\in E(G)\). Taking the latter two arguments together with the observation that there is no leaf with color \(s_1\) incident to the root \(\rho _T\), we obtain \(N(x')=N(x)=\{z\}\) in \((G,\sigma )\); a contradiction to the \({\mathsf {S} }\)-thinness of \((G,\sigma )\).
We proceed with showing Statement (ii). Repeating the latter arguments, one easily checks that \(N(x_1)=\{z\}\) for any vertex \(x_1\in L(T(v_1))\) with \(\sigma (\mathsf {child} (\mathsf {par} (x_1))\cap L)=\{r\}\). However, since \((G,\sigma )\) is \({\mathsf {S} }\)-thin, we cannot have a further vertex \(x_1\in L(T(v_1))\) with \(N(x_1)=\{z\} = N(x)\). Hence, there is exactly one \(x\in L[r]\cap L(T(v_1))\) with \(\mathsf {child} (\mathsf {par} (x))\cap L =\{x\}\) to which Rule (r) can be applied. Moreover, the existence of \(z\in \mathsf {child} (\rho _T)\cap L[s_2]\) immediately implies that Property (\(\star \)) in Definition 12 is satisfied for every \(w\in V^0(T(v_2))\) with \(\sigma (\mathsf {child} (w)\cap L) = \{r\}\). Thus, Statement (ii) is satisfied. \(\square \)
Lemma 21
If a connected \({\mathsf {S} }\)-thin 3-RBMG can be explained by tree of Type (II), then it can be explained by a tree of Type (II\(^*\)).
Proof
Assume that \((T,\sigma )\) is of Type (II) and that \(G(T,\sigma )\) is a connected \({\mathsf {S} }\)-thin 3-RBMG. Let \(S=\{r,s,t\}\) be the color set of \(L:=L(T)\) and \(v_1,v_2\in \mathsf {child} (\rho _T)\) with \(\sigma (L(T(v_1)))=\{r,s\}\) and \(\sigma (L(T(v_2)))=\{r,t\}\). If \((T,\sigma )\) is already of Type (II\(^*\)), then the statement is trivially true.
Now suppose that \((T,\sigma )\) is not of Type (II\(^*\)). Lemma 20 implies that there is exactly one leaf \(x\in L[r]\) to which Rule (r) can be applied. Hence, by using Rule (r) and thus re-attaching x to the root, one obtains a tree \((T',\sigma )\) of Type (II\(^*\)). In particular, Lemma 20 implies that x is the only vertex with color r in \((T',\sigma )\) incident to the root. W.l.o.g. assume that \(x\in L(T(v_1))\). Note, in particular, that the necessity of relocating x implies \(L[s]{\setminus } L(T(v_1))=\emptyset \) (cf. Rule (r)), i.e., \(L[s]\subseteq L(T(v_1))\). Thus, \(\mathsf {child} (\mathsf {par} (x))\cap L=\{x\}\) and Lemma 19(i)+(iv) implies that \(N_s(x)=\emptyset \) in \(G(T,\sigma )\).
Since \(L=L(T')\), it suffices to show that \(E(G(T',\sigma ))=E(G(T,\sigma ))\) to prove that \((T',\sigma )\) explains \(G(T,\sigma )\). One easily checks that the only edges that may be different between both sets are those containing the leaf x.
We start by showing \(N_s(x)=\emptyset \) in \(G(T',\sigma )\). Observe first that, as we have only changed the position of vertex \(x\in L[r]\) to obtain \((T',\sigma )\), \(L[s]\subseteq L(T(v_1))\) implies \(L[s]\subseteq L(T'(v_1))\). By Lemma 8, we have \(\sigma (L(T(w))) = \{r,s\}\) for all inner vertices \(w\preceq _{T}v_1\) in T. Thus, there must be a vertex \(w\in (L(T(v_1)))\) that is incident to two leaves \(x'\) and y with \(\sigma (x') = r\) and \(\sigma (y)=s\). Since \(\{x',y\} \subseteq \mathsf {child} (\mathsf {par} (y))\), it follows \(x'\ne x\) and thus, \(x'\) has not been re-attached. The latter implies that \(\sigma (L(T'(v_1))) = \{r,s\}\) and, by construction, \({{\,\mathrm{lca}\,}}_{T'}(x,y') =\rho _{T'} \succ _{T'} v_1 \succ _{T'} {{\,\mathrm{lca}\,}}_{T'}(x',y')\) for all \(x'\in L(T'(v_1))\cap L[r]\) and \(y'\in L[s]\cap L(T'(v_1)) = L[s]\). Therefore, there is no edge between x and any \(y'\in L[s]\) in \(G(T',\sigma )\). Hence, \(N_s(x) = \emptyset \) in \(G(T',\sigma )\).
It remains to show that \(xz\in E(G(T,\sigma ))\) if and only if \(xz \in E(G(T',\sigma ))\) for this particular re-located vertex x and all \(z\in L[t]\). Since \(G(T,\sigma )\) is connected and \(N_s(x)=\emptyset \), there must exist some vertex z with color t such that \(xz\in E(G(T,\sigma ))\). Note, Lemma 19(ii) implies that there are no edges xz for all \(z\in L[t]\cap L(T(v_2))\). That is, x and \(z\in L[t]\) form an edge xz in \(G(T,\sigma )\) if and only if z is incident to the root \(\rho _T\) (cf. Lemma 19(ii)+(iv)). In particular, we have by construction of \((T',\sigma )\) that \({{\,\mathrm{lca}\,}}_{T'}(x,z) = \rho _{T'} = {{\,\mathrm{lca}\,}}_{T'}(x',z) ={{\,\mathrm{lca}\,}}_{T'}(x,z')\) for all \(x'\in L[r]\) and all \(z'\in L[t]\) and hence, \(xz\in E(G(T',\sigma ))\).
Now assume that \(xz\in E(G(T',\sigma ))\) for this particular re-located vertex x and some \(z\in L[t]\). Since x has been re-attached, we have \({{\,\mathrm{lca}\,}}_{T'}(x,z) =\rho _{T'}\). By Lemma 20, none of the vertices in \(L(T(v_2))\) has been re-attached. Hence, \(L(T'(v_2)) = L(T(v_2))\) and thus, \(\sigma (L(T(v_2))) = \{r,t\}\). Moreover, we have \(xz'\notin E(G(T',\sigma ))\) for all \(z'\in L[t]\cap L(T(v_2))\) since \({{\,\mathrm{lca}\,}}_{T'}(x,z') =\rho _{T'} \succ _{T'} {{\,\mathrm{lca}\,}}_{T'}(x',z')\) for all \(x'\in L[r]\cap L(T(v_2))\). Thus, z must be adjacent to \(\rho _{T'}\). By construction, z must be adjacent to \(\rho _{T}\). As argued above, xz in \(G(T,\sigma )\) if and only if z is incident to the root \(\rho _T\). Therefore, \(xz\in E(G(T,\sigma ))\).
In summary, \(E(G(T',\sigma ))=E(G(T,\sigma ))\) and hence, \((T',\sigma )\) explains \(G(T,\sigma )\). \(\square \)
1.2 Three classes of \({\mathsf {S} }\)-thin 3-RBMGs
We are now in the position to use these results to show that connected components of 3-RBMGs can be grouped into three disjoint graph classes that correspond to the three tree Types (I), (II), and (III). These three classes are shown in Fig. 6.
Definition 13
An undirected, connected graph \((G,\sigma )\) on three colors is of
- Type (A):
if \((G,\sigma )\) contains a \(K_3\) on three colors but no induced \(P_4\), and thus also no induced \(C_n\), \(n\ge 5\).
- Type (B):
if \((G,\sigma )\) contains an induced \(P_4\) on three colors whose endpoints have the same color, but no induced \(C_n\) for \(n\ge 5\).
- Type (C):
if \((G,\sigma )\) contains an induced \(C_6\) along which the three colors appear twice in the same permutation, i.e., (r, s, t, r, s, t).
Theorem 4
Let \((G,\sigma )\) be an \({\mathsf {S} }\)-thin connected 3-RBMG. Then \((G,\sigma )\) is either of Type (A), (B), or (C). An RBMG of Type (A), (B), and (C), resp., can be explained by a tree of Type (I), (II), and (III), respectively.
Proof
Let \((G,\sigma )\) be an \({\mathsf {S} }\)-thin connected 3-RBMG. If \(|L|=3\), then \(|\sigma (L)|=3\) implies that \((G,\sigma )\) is the complete graph \(K_3\) on three colors, i.e., a graph of Type (A). Every phylogenetic tree on three leaves explains \((G,\sigma )\), and all of them except the star are of Type (I). From here on we assume \(|L|>3\). By Lemma 18 every connected \({\mathsf {S} }\)-thin 3-RBMG \((G,\sigma )\) is explained by a tree \((T,\sigma )\) of either Type (I), (II), or (III).
Claim 1
If \((T,\sigma )\) is of Type (I), then \((G,\sigma )\)is of Type (A).
Proof of Claim 1
Let \((T,\sigma )\) be a Type (I) tree, i.e., the root \(\rho _T\) has one child v such that \(\sigma (L(T(v)))=\{r,s\}\) and all other children of \(\rho _T\) are leaves. This and \(|\sigma (L)|=3\) implies that there must be a leaf \(z\in \mathsf {child} (\rho _T)\cap L[t]\). Since \((G,\sigma )\) is \({\mathsf {S} }\)-thin, z is the only leaf of color t in \((T,\sigma )\), thus \(xz\in E(G)\) for every \(x\in L[r]\) and \(yz\in E(G)\) for every \(y\in L[s]\). In particular, Lemma 8 implies that there exists an inner vertex \(u\preceq _T v\) such that \(\mathsf {child} (u)=\{x^*,y^*\}\) with \(x^*\in L[r]\) and \(y^*\in L[s]\), thus we have \(x^*y^*\in E(G)\). Hence, the induced subgraph \(G[x^*y^*z]\) forms a \(K_3\).
It remains to show that \((G,\sigma )\) contains no induced \(C_n\), \(n\ge 5\), or \(P_4\). Since \(L[t]=\{z\}\) and \(xz,yz\in E(G)\) for any \(x\in L[r]\) and \(y\in L[s]\), we can conclude that there cannot be any induced \(P_4\), and thus no induced \(C_n\), \(n\ge 5\), either, that contains color t. Now assume, for contradiction, that there is an induced \(P_4\) that contains the two colors r, s. By construction, this \(P_4\) must have subsequent coloring (r, s, r, s), thus it contains three distinct vertices \(x,y_1,y_2\) such that \(x\in L[r]\) and \(y_1,y_2\in L[s]\) and x is adjacent to \(y_1\) and \(y_2\). Lemma 19(i) implies that \(\mathsf {par} (y_1)=\mathsf {par} (y_2)\). Hence, \(N(y_1)=N(y_2)\), which contradicts the \({\mathsf {S} }\)-thinness of \((G,\sigma )\). Thus, there exists no induced \(P_4\) and thus no induced \(C_n\) with \(n\ge 5\) containing only two colors.
Hence, \((G,\sigma )\) is of Type (A). \(\square \)
Claim 2
If \((T,\sigma )\) is of Type (II), then \((G,\sigma )\) is of Type (B).
Proof of Claim 2
Let \((T,\sigma )\) be a Type (II) tree, i.e., the root has two distinct children \(v_1,v_2\in \mathsf {child} (\rho _T)\) such that \(\sigma (L(T(v_1)))=\{r,s\}\) and \(\sigma (L(T(v_2)))=\{r,t\}\), and all other children of the root are leaves.
We start by showing that \((G,\sigma )\) contains the particular colored induced \(P_4\). Lemma 8 implies that there must be a leaf \(y_1\in L(T(v_1))\cap L[s]\) such that \(\mathsf {par} (y_1)=\mathsf {par} (x_1)\) for some \(x_1\in L(T(v_1))\cap L[r]\) and therefore \(x_1y_1\in E(G)\). Similarly, there exist two leaves \(z_1\in L(T(v_2))\cap L[t]\) and \(x_2\in L(T(v_2))\cap L[r]\) such that \(x_2z_1\in E(G)\). Lemma 19(ii) implies that \(x_1z_1\notin E(G)\) and \(x_2y_1\notin E(G)\). Clearly, \(x_1x_2\notin E(G)\) since the two vertices have the same color. Moreover, Lemma 19(iii) implies that \(y_1z_1\in E(G)\). Hence, \(\langle x_1y_1z_1x_2\rangle \) forms an induced \(P_4\) in \((G,\sigma )\) on three colors whose endpoints have the same color.
We proceed by showing that \((G,\sigma )\) does not contain an induced \(C_n\) with \(n\ge 5\). First note that Lemma 19(iii) implies \(yz\in E(G)\) for any two leaves \(y\in L[s]\), \(z\in L[t]\). Thus, \((G,\sigma )\) cannot contain an induced \(C_n\) for some \(n\ge 5\) on colors s and t only. Therefore, assume, for contradiction, that there exists an induced \(C_n\) for some fixed \(n\ge 5\) in \(G(T,\sigma )\) that contains a leaf x of color r. Note that this necessarily implies \(|N(x)|>1\) in G. Suppose first that \(x\in \mathsf {child} (\rho _T)\). Since \((T(v_1),\sigma _{|L(T(v_1))})\) and \((T(v_2),\sigma _{|L(T(v_2))})\) both contain leaves of color r, any vertex that is adjacent to x in G must be incident to \(\rho _T\) in T. Hence, as \((G,\sigma )\) is \({\mathsf {S} }\)-thin, \(|N(x)|>1\) in G implies that \(\mathsf {child} (\rho _T)\cap L =\{x,y,z\}\), where \(y\in L[s]\) and \(z\in L[t]\), i.e., we have \(N(x)=\{y,z\}\). Thus, any induced \(C_n\), \(n\ge 5\) containing x must also contain both y and z. However, as x, y, and z have the same parent in T, they clearly form a \(K_3\) in G; a contradiction to x, y, and z being part of an induced \(C_n\).
Now suppose \(x\in L(T(v_1))\cap L[r]\). Since \((T(v_2),\sigma _{|L(T(v_2))})\) contains the colors r and t, \((G,\sigma )\) cannot contain an edge xz with \(z\in L(T(v_2))\) [cf. Lemma 19(ii)]. Hence, \(N_t(x)\ne \emptyset \) if and only if there exists a leaf z of color t that is directly attached to the root \(\rho _T\). Since \(G(T,\sigma )\) is \({\mathsf {S} }\)-thin, there can be at most one leaf of color t that is attached to \(\rho _T\), thus \(|N_t(x)|\le 1\). This and \(|N(x)|>1\) in G implies that there must be a leaf \(y\in L[s]\) such that \(y\in N_s(x)\). By Lemma 19(i), this is the case if and only if \(y\in L(T(v_1))\cap L[s]\) and \(\mathsf {par} (x)=\mathsf {par} (y)\). Since \(G(T,\sigma )\) is \({\mathsf {S} }\)-thin, there exists at most one leaf of color s with this property, hence in particular \(N(x)=\{y,z\}\). Using Lemma 19(iv), we can conclude that \(yz\in E(G)\). Thus, x, y and z form a \(K_3\). Therefore, these three leaves cannot be contained together in an induced \(C_n\), \(n\ge 5\).
Since an analogous argumentation holds if \(x\in L(T(v_2))\), we conclude that there cannot be an induced \(C_n\), \(n\ge 5\) containing a leaf of color r.
In summary, G does not contain an induced \(C_n\) for \(n\ge 5\), and thus, \((G,\sigma )\) is of Type (B). \(\square \)
Claim 3
If \((T,\sigma )\) is of Type (III), then \((G,\sigma )\) is of Type (C).
Proof of Claim 3
Let \((T,\sigma )\) be a Type (III) tree, i.e., the root \(\rho _T\) has three children \(v_1,v_2,v_3\in \mathsf {child} (\rho _T)\) such that \(\sigma (L(T(v_1)))=\{r,s\}\), \(\sigma (L(T(v_2)))=\{r,t\}\), and \(\sigma (L(T(v_3)))=\{s,t\}\), and all remaining children are leaves. Again, Lemma 8 and Lemma 19(i) imply that there exist \(x_1,y_1\in L(T(v_1))\) with \(x_1y_1\in E(G)\), \(x_2,z_1\in L(T(v_2))\) with \(x_2z_1\in E(G)\) and \(y_2,z_2\in L(T(v_3))\) with \(y_2z_2\in E(G)\), where \(x_i\in L[r]\), \(y_i\in L[s]\) and \(z_i\in L[t]\). Applying Lemma 19(ii), we can in addition conclude that \(y_1z_1,x_2y_2,x_1z_2\in E(G)\), and \((G,\sigma )\) contains none of the edges \(x_1z_1\), \(x_1y_2\), \(y_1x_2\), \(y_1z_2\), \(z_1y_2\), or \(x_2z_2\). Moreover, \((G,\sigma )\) does not contain edges between vertices of the same color. Hence, \((G[C],\sigma _{|C})\) with \(C=\{x_1,y_1,z_1,x_2,y_2,z_2\}\) forms the desired induced \(C_6\). Therefore, \((G,\sigma )\) is of Type (C). \(\square \)
By definition, the three classes of 3-RBMGs (A), (B), and (C) are disjoint. Lemma 18 states that the three classes of trees (I), (II), and (III) are disjoint, hence there is a 1–1 correspondence between the tree Types (I), (II), and (III) and the graph classes (A), (B), and (C). \(\square \)
An undirected, colored graph \((G,\sigma )\) contains an induced \(K_3\), \(P_4\), or \(C_6\), respectively, if and only if \((G/{\mathsf {S} },\sigma /{\mathsf {S} })\) contains an induced \(K_3\), \(P_4\), or \(C_6\), resp., on the same colors (cf. Lemma 5). An immediate consequence of this fact is
Theorem 5
A connected (not necessarily \({\mathsf {S} }\)-thin) 3-RBMG \((G,\sigma )\) is either of Type (A), (B), or (C).
1.3 Characterization of type (A) 3-RBMGs
As an immediate consequence of Theorem 4 and the well-known properties of cographs (Corneil et al. 1981) we obtain
Observation 3
Let \((G,\sigma )\) be a connected, \({\mathsf {S} }\)-thin 3-RBMG. Then it is of Type (A) if and only if it is a cograph.
Definition 14
Let \(G=(V,E)\) be an undirected graph. A vertex \(x\in V(G)\) such that \(N(x)=V{\setminus } \{x\}\) is a hub-vertex.
Lemma 22
A properly vertex colored, connected, \({\mathsf {S} }\)-thin graph \((G,\sigma )\) on three colors with vertex set L is a 3-RBMG of Type (A) if and only if \(G \notin {\mathcal {P}}_3\) and it satisfies the following conditions:
- (A1)
G contains a hub-vertex x, i.e., \(N(x)=V(G){\setminus } \{x\}\)
- (A2)
\(|N(y)|<3\) for every \(y\in V(G){\setminus } \{x\}\).
Proof
By definition, a 3-RBMG is properly colored and has \(|L|\ge 3\) vertices. If \(|L|=3\) there are only two connected graphs: \(K_3\) and \(P_3\). Both satisfy (A1) and (A2) since the three vertices have distinct colors. However, only \(K_3\) is a 3-RBMG: it is explained by any tree on three leaves with pairwise distinct colors. From here on we assume \(|L|\ge 4\).
We start with the “only-if-direction” and show that every 3-RBMG of Type (A) satisfies (A1) and (A2). We set \(S=\{r,s,t\}\), and assume that \((G,\sigma )\) is a 3-RBMG of Type (A). Theorem 4 implies that there exists a tree \((T,\sigma )\) with root \(\rho _T\) explaining \((G,\sigma )\) that is of Type (I), i.e., there is a vertex \(v\in \mathsf {child} (\rho _T)\) such that \(\sigma (L(T(v)))=\{s,t\}\) and \(\mathsf {child} (\rho _T){\setminus } \{v\}\subset L\). Thus every leaf x with color \(\sigma (x)=r\) is a child of \(\rho _T\). Since \((G,\sigma )\) is \({\mathsf {S} }\)-thin, this implies \(|L[r]|=1\) and therefore, \(xy\in E(G)\) for every \(y\ne x\), hence (A1) is satisfied. In order to show (A2), consider \(y\in V(G){\setminus } \{x\}\), where x is again the unique vertex with color r. Since \((G,\sigma )\) is properly colored, \(\sigma (y)\ne r\). W.l.o.g., let \(\sigma (y)=s\). Assume, for contradiction, that \(|N(y)|\ge 3\). Then there are at least two distinct vertices \(z,z'\in N_t(y)\). Assume first that \(y\in L(T(v))\). Hence, there is \(z^*\in L[t]\) with \({{\,\mathrm{lca}\,}}(y,z^*)\preceq v \prec \rho _T\). Hence, we must have \(z,z'\in L(T(v))\). However, Lemma 19(i) implies that z and \(z'\) must be siblings and therefore \(N(z)=N(z')\); a contradiction, since \((G,\sigma )\) was assumed to be \({\mathsf {S} }\)-thin. Now assume that \(y\in \mathsf {child} (\rho _T)\). Then, Lemma 19(iv) and \(z,z'\in N_t(y)\) imply that z and \(z'\) both have to be adjacent to \(\rho _T\); again this contradicts the assumption that \((G,\sigma )\) is \({\mathsf {S} }\)-thin. Thus, (A2) is satisfied.
We proceed with showing the “if-direction”. Suppose \((G,\sigma )\) is a properly vertex colored, connected, \({\mathsf {S} }\)-thin graph satisfying (A1) and (A2). In order to show that \((G,\sigma )\) is a Type (A) RBMG it suffices, by Theorem 4, to construct a Type (I) tree that explains \((G,\sigma )\). Let x be a vertex that is adjacent to all others, which exists by \(\text {(A1)} \). Assume w.l.o.g. that \(\sigma (x)=r\). Since \((G,\sigma )\) is \({\mathsf {S} }\)-thin and it does not contain edges between vertices of the same color, x must be the only vertex of color r. We define \(L_2:=\{y \mid y\ne x, |N(y)|=2\}\). Since \(|L|>3\) and thus \(|N(x)|\ge 3\), we have \(x\in L{\setminus } L_2\). Note, each vertex is adjacent to x and thus, \(N(y) = \{x,z\}\) for all \(y\in L_2\) and some vertex \(z\in L[t]\), \(t\ne \sigma (y)\). Property (A2) implies that there are \(|L{\setminus } L_2|-1\) vertices with degree 1, all incident to x. Since \((G,\sigma )\) is \({\mathsf {S} }\)-thin and \(|S|=3\), there are at most two vertices with degree 1, at most one of each color different from \(\sigma (x)\), and thus \(|L{\setminus } L_2|\le 3\).
We first construct a caterpillar \((T_2,\sigma _{|L_2})\) with leaf set \(L_2\) and root \(\rho _{T_2}\) such that \(\mathsf {par} (y)=\mathsf {par} (z)\) for any \(y,z\in L_2\) with \(\sigma (y)\ne \sigma (z)\) if only if \(yz\in E(G)\). As \(N(y) = \{x,z\}\) for all \(y\in L_2\) and some vertex \(z\in L[t]\), \(t\ne \sigma (y)\), we can conclude that each connected component of \((G[L_2], \sigma _{|L_2})\) is a single edge yz. Thus, it is easy to see that \((T_2,\sigma _{|L_2})\) explains \((G[L_2], \sigma _{|L_2})\).
For the construction of \((T,\sigma )\), we then distinguish two cases: (i) If \(L{\setminus } L_2=\{x,w_1\}\), then \((T,\sigma )\) is obtained by attaching the vertices x and \(w_1\) as well as \(\rho _{T_2}\) as children of the root \(\rho _T\). (ii) If \(L{\setminus } L_2 = \{x,w_1,w_2\}\) for distinct vertices x, \(w_1\), and \(w_2\) in \((G,\sigma )\), we first build an auxiliary tree \((T',\sigma _{|L_2\cup \{w_2\}})\) with root \(\rho _{T'}\) by attaching \(\rho _{T_2}\) and vertex \(w_2\) to \(\rho _{T'}\). The tree \((T,\sigma )\) is then constructed from \((T',\sigma _{|L_2\cup \{w_2\}})\) by attaching x, the other vertex \(w_1\) and \(\rho _{T'}\) as children of \(\rho _T\). It remains to show that \((T,\sigma )\) explains \((G,\sigma )\). By construction, \((T,\sigma )\) is a tree of Type (I) where the vertices \(\rho _{T_2}\) and \(\rho _{T'}\) play the role of v in Definition 12 in Case (i) and (ii), respectively. In the following let \(v=\rho _{T_2}\) or \(v= \rho _{T'}\) depending on whether we have Case (i) and (ii).
Theorem 4 implies that \(G(T,\sigma )\) is 3-RBMG of Type (A). It is easy to see that \(G(T,\sigma )[L_2] = (G[L_2], \sigma _{|L_2})\). Any remaining edges in \(G(T,\sigma )\) are thus adjacent to vertices in \(L{\setminus } L_2\). We first consider edges that may be incident to vertex x in \(G(T,\sigma )\). Since \({{\,\mathrm{lca}\,}}_T(z, x) = \rho _T\) and \(r\notin \sigma (L(T(v)))\), we have \(xz \in E(G(T,\sigma ))\) for all \(z\in L{\setminus } \{x\}\). Hence, (A1) is satisfied by x in \(G(T,\sigma )\).
Now, consider edges that may be incident to vertex \(w_1\) in \(G(T,\sigma )\). First note, that in both Cases (i) and (ii), the vertex \(w_1\) is adjacent to the root \(\rho _T\) in \((T,\sigma )\). Since \((T,\sigma )\) is a tree of Type (I), we can apply Lemma 19(i) to conclude that there are no edges in \(G(T,\sigma )\) between \(w_1\) and any vertex in L(T(v)). This and the arguments above show that \(N(w_1)=\{x\}\). In other words, \(w_1z \in E(G(T,\sigma ))\) if and only if \(w_1z \in E(G)\) for all \(z\in L\). This in particular shows \((G,\sigma )=G(T,\sigma )\) conforms to Case (i).
Finally, assume Case (ii) and consider edges that are incident to vertex \(w_2\) in \((G,\sigma )\) By construction, \(s,t\in \sigma (L_2)\). Since \({{\,\mathrm{lca}\,}}(w_2,z) =v \succ _T \rho _{T_2} \succeq {{\,\mathrm{lca}\,}}(w',z)\) for all \(w',z\in L_2\) with \(\sigma (w_2)=\sigma (w) \ne \sigma (z)\), we can conclude that \(w_2\) is not adjacent to any other vertex in \(L_2\). This and the arguments above show that \(N(w_2)=\{x\}\). Therefore, \(w_2z \in E(G(T,\sigma ))\) if and only if \(w_1z \in E(G)\) for all \(z\in L\).
In summary, \(G(T,\sigma )=(G,\sigma )\). Therefore, \((G,\sigma )\) is of Type (A). \(\square \)
For later reference, we record a simple property of hub-vertices.
Corollary 6
Let x be a hub-vertex of some connected \({\mathsf {S} }\)-thin 3-RBMG \((G,\sigma )\) of Type (A) with vertex set L and \(|L|>3\). Then, x is the only vertex of its color in \((G,\sigma )\), i.e., \(L[\sigma (x)]= \{x\}\). Moreover, for any \((T,\sigma )\) explaining \((G,\sigma )\), x must be incident to the root of T.
Proof
Since \((G,\sigma )\) does not contain edges between vertices of the same color, the first statement immediately follows from Property (A1) and \({\mathsf {S} }\)-thinness of \((G,\sigma )\).
For the second statement, let \((T,\sigma )\) be an arbitrary tree with root \(\rho _T\) that explains \((G,\sigma )\). Let \(v\in \mathsf {child} (\rho _T)\) with \(x\preceq _T v\). Assume, for contradiction, \(v\ne x\). Thus Lemma 8 implies that there exists a leaf \(y\in L\) with \(\sigma (y)\ne \sigma (x)\) such that \(y\preceq _T v\). Then, since x is connected to any vertex in \(L{\setminus } \{x\}\), all vertices of color \(\sigma (y)\) must be contained in the subtree T(v); otherwise \({{\,\mathrm{lca}\,}}_T(x,y)\prec _T {{\,\mathrm{lca}\,}}_T(x,y')=\rho _T\) for some vertex \(y'\in L[\sigma (y)]\), \(y'\ne y\), which yields a contradiction to \(xy'\in E(G)\). As \((T,\sigma )\) is phylogenetic, the root \(\rho _T\) has at least two different children, i.e., there is some \(w\in \mathsf {child} (\rho _T)\), \(w\ne v\). Let \(r\ne \sigma (x),\sigma (y)\) be the third color in \((G,\sigma )\). We already argued \(\sigma (x),\sigma (y)\notin \sigma (L(T(w)))\), thus \(\sigma (L(T(w)))=\{r\}\). In particular, since \((G,\sigma )\) is \({\mathsf {S} }\)-thin, Lemma 8 implies that w must be a leaf. Since \((G,\sigma )\) is connected, we can apply the same arguments as for \(L[\sigma (y)]\) to conclude that \(r\notin \sigma (L(T(v)))\), thus \(|L[r]|=1\). Since x is the only leaf of its color in \((T,\sigma )\) and \(\sigma (L(T(v)))=\{\sigma (x),\sigma (y)\}\), we can again apply Lemma 8 to conclude that \(|L[\sigma (y)]|=1\). In summary, we have therefore shown \(|L|=3\); a contradiction. Hence, x must be incident to \(\rho _T\). \(\square \)
Lemma 23
Let \((G,\sigma )\) be an \({\mathsf {S} }\)-thin graph satisfying (A1) and (A2). Then G is a cograph.
Proof
Since G contains a hub-vertex by (A1), it can be written as join \(G'{{\,\mathrm{\triangledown }\,}}K_1\), where the \(K_1\) corresponds to the hub-vertex. As a consequence of (A2), \((G',\sigma )\) is a 2-colored graph with vertex degree at most 1. The number of isolated vertices in \(G'\) cannot exceed 2, one of each color, since otherwise two vertices that are isolated in \(G'\) would have the same color and thus share the hub as their only neighbor in G, contradicting \({\mathsf {S} }\)-thinness of \((G,\sigma )\). Hence, \(G'\) is the disjoint union of an arbitrary number of \(K_2\) and at most two copies of \(K_1\):  with \(0\le n_1\le 2\) and \(n_2\ge 0\). Thus G is a cograph (Corneil et al. 1981). \(\square \)
with \(0\le n_1\le 2\) and \(n_2\ge 0\). Thus G is a cograph (Corneil et al. 1981). \(\square \)
1.4 Characterization of type (B) 3-RBMGs
Definition 15
Let \((G,\sigma )\) be an undirected, connected, properly colored, \({\mathsf {S} }\)-thin graph with vertex set L and color set \(\sigma (L)=\{r,s,t\}\), and assume that \((G,\sigma )\) contains the induced path \(P:=\langle {\hat{x}}_1 {\hat{y}} {\hat{z}} {\hat{x}}_2 \rangle \) with \(\sigma ({\hat{x}}_1)=\sigma ({\hat{x}}_2)=r\), \(\sigma ({\hat{y}})=s\), and \(\sigma ({\hat{z}})=t\). Then \((G,\sigma )\) is B-like w.r.t. P if (i) \(N_{r}({\hat{y}})\cap N_{r}({\hat{z}})=\emptyset \), and (ii) G does not contain an induced cycle \(C_n\), \(n\ge 5\).
For a 3-colored, \({\mathsf {S} }\)-thin graph \((G,\sigma )\) that is B-like w.r.t. the induced path \(P:=\langle {\hat{x}}_1 {\hat{y}} {\hat{z}} {\hat{x}}_2 \rangle \) we define the following subsets of vertices:
The first subscripts t and s refer to the color of the vertices \({\hat{z}}\) and \({\hat{y}}\), respectively, that “anchor” the \(P_3\)s within the defining path P. The second index identifies the color of the vertices in the respective set, since by definition we have \(L_{t,s}^{P}\subseteq L[s]\), \(L_{t,r}^{P}\subseteq L[r]\), \(L_{s,t}^{P}\subseteq L[t]\) and \(L_{s,r}^{P}\subseteq L[r]\). Furthermore, we set
By definition, \(L_{s,r}^P=L_s^P\cap L[r]\), \(L_{t,r}^P=L_t^P\cap L[r]\), \(L_{s,t}^P=L_s^P\cap L[t]\), and \(L_{t,s}^P=L_t^P\cap L[s]\). For simplicity we will often write \(L_*^P[i] :=L_*^P\cap L[i]\) for \(i\in \{s,t\}\).
These vertex sets arise naturally from trees of Type (II\(^*\)):
Lemma 24
Let \((G,\sigma )\) be a connected \({\mathsf {S} }\)-thin 3-RBMG of Type (B) with vertex set L and color set \(S=\{r,s,t\}\). Then, the colors can be permuted such that there are \({\hat{x}}_1, {\hat{x}}_2\in L[r]\), \({\hat{y}}\in L[s]\), \({\hat{z}} \in L[t]\) such that \((G,\sigma )\) is B-like w.r.t. \(P= \langle {\hat{x}}_1{\hat{y}}{\hat{z}} {\hat{x}}_2 \rangle \). Moreover, there exists a tree \((T,\sigma )\) of Type (II\(^*\)) explaining \((G,\sigma )\) such that
- (i)
\(L_t^P=L(T(v_1))\) and \(L_s^P=L(T(v_2))\) for \(v_1,v_2\in \mathsf {child} (\rho _T){\setminus } L\), and
- (ii)
\(L_*^P=\mathsf {child} (\rho _T)\cap L\).
Proof
Let \((G,\sigma )\) be a connected, \({\mathsf {S} }\)-thin 3-RBMG of Type (B). Then, by Lemmas 18 and 21, there is a tree \((T,\sigma )\) with root \(\rho _T\) explaining \((G,\sigma )\) that is of Type (II\(^*\)). In particular, the colors can be chosen such that there are \(v_1,v_2\in \mathsf {child} (\rho _T)\) with \(\sigma (L(T(v_1)))=\{r,s\}\), \(\sigma (L(T(v_2)))=\{r,t\}\), and \(\mathsf {child} (\rho _T){\setminus } \{v_1,v_2\}\subset L\). Applying the same argumentation as in the proof of Theorem 4 (Claim 2), we conclude that there are leaves \({\hat{x}}_1,{\hat{y}} \prec _T v_1\) and \({\hat{x}}_2,{\hat{z}}\prec _T v_2\), where \({\hat{x}}_1,{\hat{x}}_2\in L[r]\), \({\hat{y}}\in L[s]\), \({\hat{z}}\in L[t]\), such that \(\langle {\hat{x}}_1{\hat{y}}{\hat{z}}{\hat{x}}_2\rangle \) is an induced \(P_4\) in G. By \({\mathsf {S} }\)-thinness of \((G,\sigma )\) and Lemma 19(i), we have \(N_r({\hat{y}})=\{{\hat{x}}_1\}\) and \(N_r({\hat{z}})=\{{\hat{x}}_2\}\), and thus \(N_r({\hat{y}})\cap N_r({\hat{z}})=\emptyset \). Since 3-RBMGs of Type (B) do not contain induced cycles on more than six vertices, \((G,\sigma )\) is B-like w.r.t. \(\langle {\hat{x}}_1{\hat{y}}{\hat{z}}{\hat{x}}_2\rangle \). It remains to show Properties (i) and (ii).
In what follows, we put for simplicity \(L_1:=L_t^P\). To establish Property (i) we treat vertices of colors s and r separately. Consider \(y\in L[s]\). We first show that \(y\in L(T(v_1))\) implies \(y\in L_1\). Clearly, since \(L(T(v_1))\) contains leaves of color r, any \(x\in N_r(y)\) must satisfy \(x\prec _T v_1\). Lemma 19(i) implies that \(x\in N_r(y)\) if and only if \(\mathsf {par} (x)=\mathsf {par} (y)\). Therefore \(|N_r(y)|\le 1\) because \((G,\sigma )\) is \({\mathsf {S} }\)-thin. If \(N_r(y)=\emptyset \), then \(y\in L_1\) by definition. Otherwise, \(N_r(y)=\{x\}\) with \(x\prec _T v_1\). By construction of \((T,\sigma )\), there is a leaf \(x'\prec _T v_2\) of color r; this implies \({{\,\mathrm{lca}\,}}({\hat{z}},x)\succ _T{{\,\mathrm{lca}\,}}({\hat{z}},x')\) and hence \(x{\hat{z}}\notin E(G)\). Since \(y{\hat{z}}\in E(G)\) by Lemma 19(iii), we have \(\langle xy{\hat{z}} \rangle \in {\mathcal {P}}_3\) and thus, \(y\in L_1\). Hence, \(L(T(v_1))\cap L[s] \subseteq L_1\cap L[s]\) as claimed. We now show that \(y\in L_1\) implies \(y\in L(T(v_1))\). To this end, consider \(y\in L_1\cap L[s]\), i.e., either \(N_r(y)=\emptyset \) or \(\langle xy{\hat{z}} \rangle \in {\mathcal {P}}_3\) for every \(x\in N_r(y)\). Assume, for contradiction, that \(y\notin L(T(v_1))\). Then y must be incident to the root \(\rho _T\). Since \(L(T(v_2))\) contains no leaf of color s, Lemma 19(iv) implies \(y{\hat{x}}_2, y{\hat{z}} \in E(G)\). Since \({\hat{x}}_2 {\hat{z}} \in E(G)\), the vertices \({\hat{x}}_2, y,{\hat{z}}\) induce a \(K_3\), thus \(\langle {\hat{x}}_2 y {\hat{z}} \rangle \notin {\mathcal {P}}_3\), and therefore \(y\notin L_1\); a contradiction. Hence, we can conclude \(L_1\cap L[s] \subseteq L(T(v_1))\cap L[s]\). In summary we therefore have \(L(T(v_1))\cap L[s] = L_1\cap L[s]\).
Consider \(x\in L[r]\). We show that \(x\in L(T(v_1))\) implies \(x\in L_1\). If there exists a leaf \(y\in L[s]\) incident to \(\mathsf {par} (x)\), then \(N_r(y)=\{x\}\) by Lemma 19(i) and \(\langle xy{\hat{z}} \rangle \in {\mathcal {P}}_3\) by Lemma 19(ii)+(iii), implying \(x\in L_1\). Otherwise, \({\mathsf {S} }\)-thinness of G implies that \(\mathsf {child} (\mathsf {par} (x))\cap L = \{x\}\). In this case, \(N_s(x)=\emptyset \) by Lemma 19(i). Moreover, since \((T,\sigma )\) is of Type (II\(^*\)) and \(\mathsf {child} (\mathsf {par} (x))\cap L=\{x\}\), we can apply Condition (\(\star \)) in Definition 12 to conclude \(L[s]{\setminus } L_{t,s}^P =L[s]{\setminus } L(T(v_1)) \ne \emptyset \), where equality holds because \(L(T(v_1))\cap L[s] = L_1\cap L[s]=L_{t,s}^P\). In summary, we have thus shown that \(x\in L_1\). Hence, \(L(T(v_1))\cap L[r]\subseteq L_1\cap L[r]\) as claimed. Conversely, we show that \(x\in L_1\) implies \(x\in L(T(v_1))\). Assume that \(x\in L_1\cap L[r]\). Then, by definition of \(L_1\), we have \(x\in L_{t,r}^P\). Thus, either (a) there is a leaf \(y\in L[s]\) such that \(N_r(y)=\{x\}\) and \(\langle xy {\hat{z}} \rangle \in {\mathcal {P}}_3\), or, (b) \(N_s(x)=\emptyset \) and \(L[s]{\setminus } L_{t,s}^P=L[s]{\setminus } L(T(v_1))\ne \emptyset \). In Case (a), assume first for contradiction that y is adjacent to the root \(\rho _T\). Lemma 19(iv) implies that \(x'y \in E(G)\) for any \(x'\in L(T(v_2))\cap L[r]\). Since \(L(T(v_2))\cap L[r]\ne \emptyset \) and \(|N_r(y)|=1\), we have \(L(T(v_2))\cap L[r]=\{x\}\) and thus, as \({\hat{x}}_2\in L(T(v_2))\), it follows \(x={\hat{x}}_2\). However, since \(x = {\hat{x}}_2\) and \({\hat{z}}\) are adjacent in \((G,\sigma )\), \(xy{\hat{z}}\) cannot form an induced \(P_3\). We therefore conclude that y cannot be adjacent to the root \(\rho _T\). Since \(s\notin \sigma (L(T(v_2)))\), it must thus hold that \(y\in L(T(v_1))\). Lemma 19(ii)+(iv) then implies that we have \(x\in L(T(v_1))\). In Case (b), \(L[s]{\setminus } L_{t,s}^P=L[s]{\setminus } L(T(v_1))\ne \emptyset \) implies that there exists a leaf \(y^*\in L[s]{\setminus } L(T(v_1))\). Since \(s\notin \sigma (L(T(v_2)))\), this vertex \(y^*\) must be incident to the root \(\rho _T\). On the other hand, we have \(xy^*\notin E(G)\) because \(N_s(x) = \emptyset \), hence x cannot be incident to \(\rho _T\). Applying Lemma 19(iv) thus implies \(x\in L(T(v_1))\). Therefore, \(L_1\cap L[r]=L(T(v_1))\cap L[r]\).
In summary we have shown \(L_1=L(T(v_1))\). By symmetry of the definitions, analogous arguments imply \(L_s^P = L(T(v_2))\), completing the proof of statement (i). Property (ii) now immediately follows from \(\mathsf {child} (\rho _T)\cap L= L{\setminus } (L(T(v_1))\cup L(T(v_2)))= L{\setminus } (L_t^P\cup L_s^P)\). \(\square \)
The following remark will be useful for the design of algorithms to recognize Type (B) RBMGs. It implies, in particular, that testing whether \((G,\sigma )\) is B-like w.r.t. some induced \(P_4\) strongly depends on the reference \(P_4\), i.e., it is necessary to identify all \(P_4\)s in \((G,\sigma )\).
Observation 4
A connected \({\mathsf {S} }\)-thin 3-RBMG \((G,\sigma )\) of Type (B) may contain distinct induced \(P_4\)s P and \(P'\), both of the form (r, s, t, r) for distinct colors r, s, t, such that \((G,\sigma )\) is B-like w.r.t. P but not B-like w.r.t. \(P'\). An example is given in Fig. 7.
Using the previous result, we obtain the following characterization for 3-colored RBMGs of Type (B).
Lemma 25
Let \((G,\sigma )\) be an undirected, connected, \({\mathsf {S} }\)-thin and properly 3-colored graph with color set \(S=\{r,s,t\}\) and let \(x\in L[r]\), \(y\in L[s]\) and \(z\in L[t]\). Then, \((G,\sigma )\) is a 3-RBMG of Type (B) if and only if the following conditions are satisfied, after possible permutation of the colors:
- (B1)
\((G,\sigma )\) is B-like w.r.t. \(P = \langle {\hat{x}}_1{\hat{y}}{\hat{z}} {\hat{x}}_2 \rangle \) for some \({\hat{x}}_1, {\hat{x}}_2\in L[r]\), \({\hat{y}}\in L[s]\), \({\hat{z}} \in L[t]\),
- (B2.a)
If \(x\in L_*^P\), then \(N(x)=L_*^P{\setminus }\{x\}\),
- (B2.b)
If \(x\in L_t^P\), then \(N_s(x)\subset L_t^P\) and \(|N_s(x)|\le 1\), and \(N_t(x)= L_*^P[t]\),
- (B2.c)
If \(x\in L_s^P\), then \(N_t(x)\subset L_s^P\) and \(|N_t(x)|\le 1\), and \(N_s(x)= L_*^P[s]\)
- (B3.a)
If \(y\in L_*^P\), then \(N(y)=L_s^P\cup (L_*^P{\setminus }\{y\})\),
- (B3.b)
If \(y\in L_t^P\), then \(N_r(y)\subset L_t^P\) and \(|N_r(y)|\le 1\), and \(N_t(y)=L[t]\),
- (B4.a)
If \(z\in L_*^P\), then \(N(z)=L_t^P\cup (L_*^P{\setminus }\{z\})\),
- (B4.b)
If \(z\in L_s^P\), then \(N_r(z)\subset L_s^P\) and \(|N_r(z)|\le 1\), and \(N_s(z)=L[s]\).
In particular, \(L_t^P\), \(L_s^P\), and \(L_*^P\) are pairwise disjoint and \({\hat{x}}_1, {\hat{y}} \in L_t^P\), \({\hat{x}}_2,{\hat{z}}\in L_s^P\).
Proof
Suppose first that \((G,\sigma )\) satisfies Conditions (B1) - (B4.b). By Condition (B1), \((G,\sigma )\) is B-like, thus in particular it contains no induced \(C_n\), \(n\ge 5\). Therefore, if \((G,\sigma )\) is an RBMG, then it must be of Type (B).
In order to prove that \((G,\sigma )\) is indeed an RBMG, we construct a tree \((T,\sigma )\) based on the sets \(L_t^P\), \(L_s^P\), and \(L_*^P\) and show that it explains \((G,\sigma )\). To this end, we show first that the sets \(L_t^P\), \(L_s^P\), and \(L_*^P\) are pairwise disjoint. By definition, \(L_*^P\) is disjoint from \(L_t^P\) and \(L_s^P\). Moreover, by definition, \(\sigma (L_t^P)\cap \sigma (L_s^P)=\{r\}\). Thus, it suffices to show that any vertex \(x\in L[r]{\setminus } L_*^P\) is is contained in exactly one of the sets \(L_t^P\) or \(L_s^P\). Assume, for contradiction, that there exists a leaf x that is contained in both \(L_t^P\) and \(L_s^P\). Hence, \(x\in L_{t,r}^P\cap L_{s,r}^P\). Then, by definition of \(L_{t,r}^P\), either (a) \(N_s(x)=\emptyset \) and \(L[s]{\setminus } L_{t,s}^P\ne \emptyset \), or (b) \(N_r(y)=\{x\}\) and \(\langle xy{\hat{z}} \rangle \in {\mathcal {P}}_3\) for some \(y\in L[s]\). Suppose first Case (a). Since \(N_s(x)=\emptyset \) and \((G,\sigma )\) is connected, there must be a vertex \(z\in L[t]\) such that \(xz\in E(G)\). Since \(x\in L_s^P\), Condition (B2.c) implies \(N_t(x)=\{z\}\). Furthermore, by Condition (B2.c), \(N_t(x)\subset L_s^P\) and thus, \(z\in L_s^P\). On the other hand, \(x\in L_t^P\) and (B2.b) imply \(z\in L_*^P\); a contradiction since \(L_s^P\) and \(L_*^P\) are disjoint. Analogously, in Case (b), Condition (B2.b) implies \(y\in L_t^P\), whereas \(y\in L_*^P\) by Condition (B2.c), which again yields a contradiction. We therefore conclude that \(L_t^P\), \(L_s^P\), and \(L_*^P\) are disjoint.
Moreover, for the construction of \((T,\sigma )\), we show that \(G[L_i^P]\) is the disjoint union of an arbitrary number of \(K_1\)’s and \(K_2\)’s with \(i\in \{s,t\}\). By definition of \(L_t^P\), we have \(\sigma (L_t^P) \subseteq \{r,s\}\). Since \(N_s(x) \subset L_t^P\) and \(|N_s(x)|\le 1\) for any \(x\in L_{t,r}^P\) by (B2.b) as well as \(N_r(y) \subset L_t^P\) and \(|N_r(y)|\le 1\) for any \(y\in L_{t,s}^P\) by (B3.b). Therefore, any vertex of \(L_t^P\) has at most one neighbor in \(L_t^P\). Similar arguments and application of Properties (B2.c), resp., (B4.b) show that any vertex of \(L_s^P\) has at most one neighbor in \(L_s^P\). Thus, \(G[L_i^P]\) is the disjoint union of an arbitrary number of \(K_1\)’s and \(K_2\)’s with \(i\in \{s,t\}\).
We are now in the position to construct a tree \((T,\sigma )\) based on the sets \(L_t^P\), \(L_s^P\), and \(L_*^P\) and to show that it explains \((G,\sigma )\). First, for \(i\in \{s,t\}\), we construct a caterpillar \((T_i,\sigma _i)\), with root \(\rho _{T_i}\), on the leaf set \(L_i^P\) such that \(\mathsf {par} (a)=\mathsf {par} (b)\) for any \(a,b\in L_i^P\) with \(\sigma (a)\ne \sigma (b)\) if and only if \(ab\in E(G)\). Since \(G[L_i^P]\) is the disjoint union of an arbitrary number of \(K_1\)’s and \(K_2\)’s, the tree \(T_i\) is well-defined. It is, however, not unique as the order of inner vertices in \(T_i\) is arbitrary. Then \((T,\sigma )\) is given by attaching \(\rho _{T_t}\), \(\rho _{T_s}\) and \(L_*^P\) to the root \(\rho _T\). Since \(L_t^P\), \(L_s^P\), and \(L_*^P\) are pairwise disjoint, the tree \((T,\sigma )\) is well-defined.
We now show that \((T,\sigma )\) is of Type (II) by verifying that \(\sigma (L_t^P)=\{r,s\}\) and \(\sigma (L_s^P) = \{r,t\}\). It is easy to see that \({\hat{z}}\in L_{s,t}^P\) and \({\hat{y}}\in L_{t,s}^P\) and thus, \(s\in \sigma (L_t^P)\) and \(t\in \sigma (L_s^P)\). Since \({\hat{z}}\in L_{s}^P\), we can apply Property (B4.b) to conclude that \({\hat{x}}_2\in N_r({\hat{z}}) \subset L_s^P\). Hence, \(r\in \sigma (L_s^P)\). Applying (B3.b), one similarly shows \({\hat{x}}_1\in L_{t}^P\) and thus, \(r\in \sigma (L_t^P)\). By construction, \(t\notin \sigma (L_t^P)\) and \(s\notin \sigma (L_s^P)\). Thus, \(\sigma (L_t^P)=\{r,s\}\) and \(\sigma (L_s^P) = \{r,t\}\) and hence, \((T,\sigma )\) is of Type (II).
It remains to show that \(G(T,\sigma )=(G,\sigma )\). To this end, we put \(L_1 :=L_t^P\) and \(L_2 :=L_s^P\) as well as \(v_1 :=\rho _{T_t}\) and \(v_2 :=\rho _{T_s}\). Therefore, \(L_1 = L(T(v_1))\) and \(\sigma (L_1) = \{r,s\}\) as well as \(L_2 = L(T(v_2))\) and \(\sigma (L_1) = \{r,t\}\).
In order to show \(G(T,\sigma )=(G,\sigma )\), we first consider the adjacencies between vertices L[s] and L[t]. By Conditions (B3.a) and (B3.b), we have \(yz\in E(G)\) for any \(y\in L[s]\), \(z\in L[t]\). The same is true for \(G(T,\sigma )\) by Lemma 19(iii). Thus, the edges between vertices of color s and t in \(G(T,\sigma )\) and \( (G,\sigma )\) coincide.
Next, we show that the neighborhood w.r.t. r of any vertex of color s and t, respectively, coincide in \((G,\sigma )\) and \(G(T,\sigma )\). For each \(y\in L_1\) with \(\sigma (y)=s\), we have \({{\,\mathrm{lca}\,}}(y,x)\prec _T {{\,\mathrm{lca}\,}}(y,x')\) for any \(x\in L(T(v_1))\), \(x'\notin L(T(v_1))\) with \(\sigma (x)=\sigma (x')=r\). Therefore, \(N_r(y)\subset L_1\) in \(G(T,\sigma )\) for all \(y\in L_1\cap L[s]\). By Condition (B3.b), we also have \(N_r(y)\subset L_1\) in \((G,\sigma )\) for all \(y\in L_1\cap L[s]\). Clearly, for any \(x\in L(T(v_1))\), we have \(xy\in E(G(T,\sigma ))\) if and only if \(\mathsf {par} (x)=\mathsf {par} (y)\). Moreover we constructed \((T,\sigma )\) such that \(\mathsf {par} (x)=\mathsf {par} (y)\) if and only if \(xy\in E(G)\). Hence, the neighborhoods \(N_r(y)\) in \(G(T,\sigma )\) and \((G,\sigma )\) coincide for all \(y\in L_1\cap L[s]\). By similar arguments and application of (B4.b) one can show that the neighborhoods \(N_r(z)\) in \(G(T,\sigma )\) and \((G,\sigma )\) coincide for all \(z\in L_2\cap L[t]\).
Now suppose that \(y\in L[s]\) is not contained in \(L_1\), thus \(y\in L_*^P\), and let \(x\in L[r]\). By construction of \((T,\sigma )\), we have \({{\,\mathrm{lca}\,}}(x,y) = \rho _T\) and thus, \({{\,\mathrm{lca}\,}}(x,y)\preceq _T{{\,\mathrm{lca}\,}}(x,y')\) for any \(y'\) of color s if and only if \(x\in L_2\cup L_*^P\), hence \(N_r(y)=(L_2\cup L_*^P) \cap L[r]\) in \(G(T,\sigma )\). By Condition (B3.a), we have \(N_r(y)=(L_2\cup L_*^P) \cap L[r]\) in \((G,\sigma )\) as well. Hence, the neighborhoods \(N_r(y)\) coincide in \(G(T,\sigma )\) and \((G,\sigma )\) for all \(y\in L_*^P\). Similar arguments and application of (B4.a) shows that the neighborhoods \(N_r(z)\) in \(G(T,\sigma )\) and \((G,\sigma )\) coincide for all \(z\in L_*^P\).
So far, we have shown that the neighborhoods N(y) and N(z) of all \(y\in L[s]\), resp., \(z\in L[t]\) are the same in both, \(G(T,\sigma )\) and \((G,\sigma )\). It remains to show that this is also true for vertices \(x\in L[r]\). Since \(y\in N(x)\cap L[s]\) if and only if \(x\in N(y)\cap L[r]\) and the N(y) neighborhoods for all \(y\in L[s]\) coincide in both graphs, we can conclude that \(N_s(x)\) w.r.t. \(G(T,\sigma )\) coincides with \(N_s(x)\) w.r.t. \((G,\sigma )\). The same is true for the \(N_t(x)\) neighborhoods. Hence, the N(x) neighborhoods in \(G(T,\sigma )\) and \((G,\sigma )\), resp., are identical. In summary, we have shown that \(G(T,\sigma )=(G,\sigma )\), i.e., \((T,\sigma )\) explains \((G,\sigma )\). Hence, \((G,\sigma )\) is a 3-RBMG.
Now let \((G,\sigma )\) be a 3-RBMG of Type (B). By Lemma 24, \((G,\sigma )\) is B-like w.r.t. \(\langle {\hat{x}}_1{\hat{y}}{\hat{z}} {\hat{x}}_2\rangle \) for some \({\hat{x}}_1, {\hat{x}}_2\in L[r]\), \({\hat{y}}\in L[s]\), \({\hat{z}} \in L[t]\), which proves (B1). Moreover, again by Lemma 24, the tree \((T,\sigma )\) that explains \((G,\sigma )\) can be chosen in a way that it is of Type (II\(^*\)) and satisfies \(L_1=L(T(v_1))\), \(L_2=L(T(v_2))\) for \(v_1,v_2\in \mathsf {child} (\rho _T){\setminus } L\), and \(L_*^P=\mathsf {child} (\rho _T)\cap L\). Now, careful application of Lemma 19(i)–(iv), which we leave to the reader, shows that Conditions (B2.a) to (B4.b) are satisfied. \(\square \)
We note that some conditions in Lemma 25 are redundant. For instance, (B4.a) and (B4.b) are a consequence of (B2.a)–(B3.b). We find them convenient, however, to describe the structure of Type (B) 3-RBMGs since they emphasize the symmetric structure of the conditions and somewhat simplify the arguments. We will give a non-redundant set of conditions in Theorem 6 at the end of this section.
We give here an alternative receipt to reconstruct a 3-RBMG \((G,\sigma )\) of Type (B) that is B-like w.r.t. some P as in Definition 15, based on its induced subgraphs \((G_*,\sigma _*):=(G[L_*^P],\sigma _{|L_*^P})\), \((G_1,\sigma _1):=(G[L_t^P],\sigma _{|L_t^P})\), and \((G_2,\sigma _2):=(G[L_s^P],\sigma _{|L_s^P})\). This particular reconstruction and the knowledge about the structure of Type (B) RBMGs may be potentially useful for orthology detection, more precisely for the identification of false positive and false negative orthology assignments (Geiß et al. 2019b). By (B2.a) and (B2.b), \((G_1,\sigma _1)\) and \((G_2,\sigma _2)\) are both disjoint unions of an arbitrary number of \(K_1\)’s and \(K_2\)’s. By Lemma 24 there exists a tree of Type (II\(^*\)) that explains \((G,\sigma )\) and satisfies \(L(T(v_1)) = L_t^P\), \(L(T(v_2)) = L_s^P\) for \(v_1,v_2\in \mathsf {child} (\rho _T)v L\), and \(L_*^P=\mathsf {child} (\rho _T)\cap L\). Hence, by Lemma 19, \((G,\sigma )\) can be obtained by inserting edges all edges ab with
- (i)
\(a\in L_t^P\), \(b\in L_s^P\) and \(\sigma (a),\sigma (b)\in \sigma (L_t^P)\triangle \sigma (L_s^P)\), where \(\triangle \) denotes the symmetric difference, and
- (ii)
\(a\in L_i^P\), \(b\in L_*^P\) and \(\sigma (b)\notin \sigma (L_i^P)\) for \(i\in \{s,t\}\)
into the disjoint union of \((G_1,\sigma _1)\), \((G_2,\sigma _2)\), and \((G_*,\sigma _*)\).
However, the assignment of leaves to one of the sets \(L_t^P\), \(L_s^P\), or \(L_*^P\) strongly depends on the choice of the corresponding induced \(P_4\). We refer to Fig. 13 for an example. The 3-RBMG \((G,\sigma )\) contains the induced \(P_4\)s \(\langle a_1b_1c_1a_2 \rangle \) and \(\langle a_1c_2b_2a_2 \rangle \), where \(a_1,a_2\in L[r]\), \(b_1,b_2\in L[s]\) and \(c_1,c_2\in L[t]\). If \(L_t^P\), \(L_s^P\), or \(L_*^P\) are defined w.r.t. \(P = \langle a_1b_1c_1a_2 \rangle \), then one obtains \(L_t^P=\{a_1,b_1\}\), \(L_s^P=\{a_2,c_1\}\), and \(L_*^P=\{b_2,c_2\}\), from which one constructs the tree \((T_1,\sigma )\). On the other hand, if \(P = \langle a_1c_2b_2a_2 \rangle \) is chosen as the corresponding \(P_4\), it yields \(L_t^P=\{a_1,c_2\}\), \(L_s^P=\{a_2,b_2\}\), and \(L_*^P=\{b_1,c_1\}\) and the tree \((T_2,\sigma )\).
We will return to the induced \(P_4\)s with endpoints of the same color in Sect. E below. We shall see that they fall into two distinct classes, which we call good and bad. All good \(P_4\)s in \((G,\sigma )\) imply the same vertex sets \(L_t^P\), \(L_s^P\), and \(L_*^P\). In contrast, different bad \(P_4\)s results in different vertex sets.
1.5 Characterization of type (C) 3-RBMGs
The construction of Type (B) 3-RBMGs can be extended to a similar characterization of Type (C) 3-RBMGs.
Definition 16
Let \((G,\sigma )\) be an undirected, connected, properly colored, \({\mathsf {S} }\)-thin graph. Moreover, assume that \((G,\sigma )\) contains the hexagon \(H:=\langle {\hat{x}}_1 {\hat{y}}_1 {\hat{z}}_1 {\hat{x}}_2 {\hat{y}}_2 {\hat{z}}_2 \rangle \) such that \(\sigma ({\hat{x}}_1)=\sigma ({\hat{x}}_2) =r\), \(\sigma ({\hat{y}}_1)=\sigma ({\hat{y}}_2)=s\), and \(\sigma ({\hat{z}}_1)=\sigma ({\hat{z}}_2) =t\). Then, \((G,\sigma )\) is C-like w.r.t. H if there is a vertex \(v\in \{{\hat{x}}_1 ,{\hat{y}}_1, {\hat{z}}_1, {\hat{x}}_2 ,{\hat{y}}_2, {\hat{z}}_2\}\) such that \(|N_c(v)|>1\) for some color \(c\ne \sigma (v)\). Suppose that \((G,\sigma )\) is C-like w.r.t. \(H =\langle {\hat{x}}_1 {\hat{y}}_1 {\hat{z}}_1 {\hat{x}}_2 {\hat{y}}_2 {\hat{z}}_2 \rangle \) and assume w.l.o.g. that \(v={\hat{x}}_1\) and \(c=t\), i.e., \(|N_t({\hat{x}}_1)|>1\). Then we define the following sets:
Again, there is a close connection between these vertex sets and trees of Type (III).
Lemma 26
Let \((G,\sigma )\) be an \({\mathsf {S} }\)-thin 3-RBMG of Type (C) with \(|L|>6\) and color set \(S=\{r,s,t\}\). Then, up to permutation of colors, \((G,\sigma )\) is C-like w.r.t. the hexagon \(H = \langle {\hat{x}}_1{\hat{y}}_1{\hat{z}}_1 {\hat{x}}_2 {\hat{y}}_2 {\hat{z}}_2 \rangle \) for some \({\hat{x}}_i\in L[r]\), \({\hat{y}}_i\in L[s]\), \({\hat{z}}_i \in L[t]\) and there exists a tree \((T,\sigma )\) of Type (III) explaining \((G,\sigma )\) such that
- (i)
\(L_t^H=L(T(v_1))\), \(L_s^H=L(T(v_2))\), and \(L_r^H=L(T(v_3))\) where \(v_1,v_2, v_3\in \mathsf {child} (\rho _T)\), and
- (ii)
\(L_*^H=\mathsf {child} (\rho _T)\cap L\).
Proof
We argue along the lines of the proof of Lemma 24. Let \((G,\sigma )\) be a 3-RBMG of Type (C). Then, Lemma 18 implies that there exists a tree \((T,\sigma )\) with root \(\rho _T\) explaining \((G,\sigma )\) that is of Type (III), thus in particular there are vertices \(v_1,v_2,v_3\in \mathsf {child} (\rho _T)\) with \(\sigma (L(T(v_1)))=\{r,s\}\), \(\sigma (L(T(v_2)))=\{r,t\}\), and \(\sigma (L(T(v_3)))=\{s,t\}\), and \(\mathsf {child} (\rho _T){\setminus } \{v_1,v_2, v_3\}\subset L\). Similar argumentation as in the proof of Theorem 4 (Claim 3) shows that there are leaves \({\hat{x}}_1,{\hat{y}}_1 \prec _T v_1\), \({\hat{x}}_2,{\hat{z}}_1\prec _T v_2\), and \({\hat{y}}_2, {\hat{z}}_2\prec _T v_3\), where \({\hat{x}}_1,{\hat{x}}_2\in L[r], {\hat{y}}_1, {\hat{y}}_2\in L[s], {\hat{z}}_1, \hat{z}_2\in L[t]\), such that \(\langle {\hat{x}}_1{\hat{y}}_1{\hat{z}}_1{\hat{x}}_2{\hat{y}}_2 {\hat{z}}_2 \rangle \) is a hexagon. Since \(|L|>6\), there exists an additional leaf \(z'\). W.l.o.g. we can assume that this additional vertex has color \(\sigma (z')=t\). Since \((T,\sigma )\) is of Type (III), there are three mutually exclusive cases: \(z'\prec _T v_2\) or \(z'\prec _T v_3\) or \(z'\) is incident to the root \(\rho _T\).
Suppose first that \(z'\prec _T v_2\). Lemma 19(ii) implies \(z'{\hat{y}}_1\in E(G)\). Since in addition \({\hat{z}}_1{\hat{y}}_1\in E(G)\), we can conclude \(|N_t({\hat{y}}_1)|>1\). Similarly, if \(z'\prec _T v_3\), then Lemma 19(ii) implies \(z'{\hat{x}}_1\in E(G)\) and thus, as \({\hat{z}}_2{\hat{x}}_1\in E(G)\), we have \(|N_t({\hat{x}}_1)|>1\). Finally, if \(z'\) is incident to the root \(\rho _T\), then Lemma 19(iv) implies \(z'{\hat{x}}_1\in E(G)\) and we again obtain \(|N_t({\hat{x}}_1)|>1\). In summary, if \(|L|>6\) and \((G,\sigma )\) is of Type (C), then there is always a hexagon H and a vertex v in H such that \(|N_c(v)|>1\) for some color \(c\ne \sigma (v)\). Therefore, \((G,\sigma )\) is C-like w.r.t. some hexagon in G.
It remains to show Properties (i) and (ii). Since \((G,\sigma )\) is C-like w.r.t. some hexagon H in G and one can always shift the vertex labels along \(H=\langle {\hat{x}}_1{\hat{y}}_1{\hat{z}}_1 {\hat{x}}_2 {\hat{y}}_2 {\hat{z}}_2 \rangle \) as well as permuting the colors in \((G,\sigma )\), we can w.l.o.g. assume \(v={\hat{x}}_1\) and \(c=t\), i.e., \(|N_t({\hat{x}}_1)|>1\). Let \(x\in L[r]\) and assume first \(x\in L(T(v_1))\). We show that this implies \(x\in L_t^H\). Lemma 19(ii) implies \(x{\hat{z}}_2\in E(G)\) and \(x{\hat{y}}_2\notin E(G)\). Since \({\hat{y}}_2{\hat{z}}_2 \in E(G)\) by definition of H, we can conclude \(\langle x{\hat{z}}_2 {\hat{y}}_2 \rangle \in {\mathcal {P}}_3\). Thus, \(x\in L_t^H\). Hence, we have \(L(T(v_1))\cap L[r] \subseteq L_t^H\cap L[r]\). Now let \(x\in L_t^H\), i.e., \(\langle x {\hat{z}}_2{\hat{y}}_2\rangle \) forms an induced \(P_3\). Since \(x {\hat{y}}_2 \notin E(G)\), Lemma 19(ii) implies that \(x \notin L(T(v_2))\). In addition, \(x {\hat{y}}_2 \notin E(G)\) and Lemma 19(iv) imply that x cannot be incident to the root \(\rho _T\). Moreover, \(x\notin L(T(v_3))\) because \(r\notin \sigma (L(T(v_3)))\) by construction of \((T,\sigma )\). Hence, x must be contained in \(L(T(v_1))\). Therefore, we have \(L(T(v_1))\cap L[r] \supseteq L_t^H\cap L[r]\), which implies \(L(T(v_1))\cap L[r] = L_t^H\cap L[r]\).
Analogously, one shows \(L(T(v_1))\cap L[s] = L_t^H\cap L[s]\) and consequently, \(L(T(v_1))= L_t^H\). By symmetry, one then obtains \(L(T(v_2)) = L_s^H\) and \(L(T(v_3)) = L_r^H\), showing property (i). Property (ii) is a direct consequence of Property (i) because \(L_*^H=L{\setminus } (L_t^H\cup L_s^H \cup L_r^H)=L{\setminus } (L(T(v_1))\cup L(T(v_2))\cup L(T(v_3)))=\mathsf {child} (\rho _T)\cap L\). \(\square \)
Lemma 27
Let \((G,\sigma )\) be an undirected, connected, \({\mathsf {S} }\)-thin, and properly 3-colored graph with color set \(S=\{r,s,t\}\) and let \(x\in L[r]\), \(y\in L[s]\) and \(z\in L[t]\). Then, \((G,\sigma )\) is a 3-RBMG of Type (C) if and only if \((G,\sigma )\) is either a hexagon or \(|L|>6\) and, up to permutation of colors, the following conditions are satisfied:
- (C1)
\((G,\sigma )\) is C-like w.r.t. the hexagon \(H = \langle {\hat{x}}_1{\hat{y}}_1{\hat{z}}_1 {\hat{x}}_2 {\hat{y}}_2 {\hat{z}}_2 \rangle \) for some \({\hat{x}}_i\in L[r]\), \({\hat{y}}_i\in L[s]\), \({\hat{z}}_i \in L[t]\) with \(|N_t({\hat{x}}_1)|>1\),
- (C2.a)
If \(x\in L_*^H\), then \(N(x)=L_r^H\cup (L_*^H{\setminus }\{x\})\),
- (C2.b)
If \(x\in L_t^H\), then \(N_s(x)\subset L_t^H\) and \(|N_s(x)|\le 1\), and \(N_t(x)= L_*^H[t]\cup L_r^H[t]\),
- (C2.c)
If \(x\in L_s^H\), then \(N_t(x)\subset L_s^H\) and \(|N_t(x)|\le 1\), and \(N_s(x)= L_*^H[s]\cup L_r^H[s]\)
- (C3.a)
If \(y\in L_*^H\), then \(N(y)=L_s^H\cup (L_*^H{\setminus }\{y\})\),
- (C3.b)
If \(y\in L_t^H\), then \(N_r(y)\subset L_t^H\) and \(|N_r(y)|\le 1\), and \(N_t(y)=L_*^H[t]\cup L_s^H[t]\),
- (C3.c)
If \(y\in L_r^H\), then \(N_t(y)\subset L_r^H\) and \(|N_t(y)|\le 1\), and \(N_r(y)=L_*^H[r]\cup L_s^H[r]\),
- (C4.a)
If \(z\in L_*^H\), then \(N(z)=L_t^H\cup (L_*^H{\setminus }\{z\})\),
- (C4.b)
If \(z\in L_s^H\), then \(N_r(z)\subset L_s^H\) and \(|N_r(z)|\le 1\), and \(N_s(z)=L_*^H[s]\cup L_t^H[s]\),
- (C4.c)
If \(z\in L_r^H\), then \(N_s(z)\subset L_r^H\) and \(|N_s(z)|\le 1\), and \(N_r(z)=L_*^H[r]\cup L_t^H[r]\).
In particular, \(L_t^H\), \(L_s^H\), \(L_r^H\), and \(L_*^H\) are pairwise disjoint and \({\hat{x}}_1, {\hat{y}}_1\in L_t^H\), \({\hat{x}}_2, {\hat{z}}_1\in L_s^H\), \({\hat{y}}_2, {\hat{z}}_2\in L_r^H\).
Proof
If \(|L|\le 6\), it follows from Theorem 4 that \((G,\sigma )\) is a 3-RBMG of Type (C) if and only if \(|L|=6\) and \((G,\sigma )\) is a hexagon. Hence, we assume that \(|L|>6\) and \((G,\sigma )\) satisfies conditions (C1)–(C4.c). As a consequence of (C1), if \((G,\sigma )\) is an RBMG, then it must be of Type (C). In order to prove that \((G,\sigma )\) is indeed an RBMG, we construct a tree \((T,\sigma )\) based on the sets \(L_t^H\), \(L_s^H\), \(L_r^H\), and \(L_*^H\) and show that \((T,\sigma )\) explains \((G,\sigma )\).
To this end, we first show that the sets \(L_t^H\), \(L_s^H\), \(L_r^H\), and \(L_*^H\) are pairwise disjoint. By definition, \(L_*^H\) is disjoint from \(L_t^H\), \(L_s^H\), and \(L_r^H\). Now, let \(x\in L[r]\) and assume that \(x\in L_t^H\). Hence, \(\langle x {\hat{z}}_2 {\hat{y}}_2 \rangle \in {\mathcal {P}}_3\) which in particular implies \(x{\hat{z}}_2 \in E(G)\). Therefore, \(\langle x {\hat{y}}_2 {\hat{z}}_2 \rangle \notin {\mathcal {P}}_3\) and thus, \(x\notin L_s^H\). Repeated analogous argumentation shows that \(L_t^H\), \(L_s^H\), and \(L_r^H\) are pairwise disjoint.
Moreover, for the construction of \((T,\sigma )\), we show that \(G[L_i^H]\) is the disjoint union of an arbitrary number of \(K_1\)’s and \(K_2\)’s with \(i\in \{r,s,t\}\). By definition of \(L_t^H\), we have \(\sigma (L_t^H) \subseteq \{r,s\}\). Since \(N_s(x) \subset L_t^H\) and \(|N_s(x)|\le 1\) for any \(x\in L_{t}^H\) by (C2.b) as well as \(N_r(y) \subset L_t^H\) and \(|N_r(y)|\le 1\) for any \(y\in L_{t}^H\) by (C3.b), any vertex of \(L_t^H\) has at most one neighbor in \(L_t^H\). Thus, \(G[L_t^H]\) is the disjoint union of an arbitrary number of \(K_1\)’s and \(K_2\)’s. Similar arguments and application of Properties (C2.c) and (C4.b), resp., (C3.c) and (C4.c), show that \(G[L_s^H]\), resp., \(G[L_r^H]\), is the disjoint union of an arbitrary number of \(K_1\)’s and \(K_2\)’s.
We are now in the position to construct a tree \((T,\sigma )\) based on the sets \(L_t^H\), \(L_s^H\), \(L_r^H\), and \(L_*^H\). First, for \(i\in \{r,s,t\}\), we construct a caterpillar \((T_i,\sigma _i)\), with root \(\rho _{T_i}\), on the leaf set \(L_i^H\) such that \(\mathsf {par} (a)=\mathsf {par} (b)\) for any \(a,b\in L_i^H\) with \(\sigma (a)\ne \sigma (b)\) if and only if \(ab\in E(G)\). Since \(G[L_i^H]\) is the disjoint union of an arbitrary number of \(K_1\)’s and \(K_2\)’s, the tree \(T_i\) is well-defined. It is, however, not unique as the order of inner vertices in \(T_i\) is arbitrary. Then \((T,\sigma )\) is given by attaching \(\rho _{T_t}\), \(\rho _{T_s}\), \(\rho _{T_r}\) and \(L_*^H\) to the root \(\rho _T\). Since \(L_t^H\), \(L_s^H\), \(L_r^H\), and \(L_*^H\) are pairwise disjoint, the tree \((T,\sigma )\) is well-defined. It is easy to verify that \({\hat{x}}_1, {\hat{y}}_1 \in L_t^H\), \({\hat{x}}_2, {\hat{z}}_1 \in L_s^H\), and \({\hat{y}}_2, {\hat{z}}_2 \in L_r^H\). Therefore, \(\sigma (L_t^H)=\{r,s\}\), \(\sigma (L_s^H) = \{r,t\}\) and \(\sigma (L_r^H) = \{s,t\}\). This implies that \((T,\sigma )\) is of Type (III). To this end, let \(v_1:=\rho _{T_t}\), \(v_2:=\rho _{T_s}\) and \(v_3:=\rho _{T_r}\) and thus \(L(T(v_1)) = L_t^H\), \(L(T(v_2)) = L_s^H\) and \(L(T(v_3)) = L_r^H\), respectively.
It remains to show that \(G(T,\sigma )=(G,\sigma )\). We first consider the adjacencies of the vertices with color r. Let \(x\in L[r]\). Suppose first \(x\in \mathsf {child} (\rho _T)\), i.e., \(x\in L_*^H\) in \((G,\sigma )\). Clearly, any leaf (with color different from \(\sigma (x)\)) that is incident to the root \(\rho _T\) is a neighbor of x in \(G(T,\sigma )\), i.e., \(L_*^H{\setminus } \{x\}\subseteq N(x)\). Moreover, since there is no leaf of color r in \(L(T(v_3))\), we have \(L_r^H\subseteq N(x)\) in \(G(T,\sigma )\) by Lemma 19(iv). Hence, \(L_r^H \cup (L_*^H{\setminus } \{x\})\subseteq N(x)\) in \(G(T,\sigma )\). Furthermore, since r is contained in \(\sigma (L(T(v_1)))\) as well as in \(\sigma (L(T(v_2)))\), we can apply Lemma 19(iv) to conclude that x is not adjacent to any vertex in \(L(T(v_1)) = L_t^H\) and \(L(T(v_2)) = L_s^H\) in \(G(T,\sigma )\). Thus, \(N(x) \subseteq L_r^H \cup (L_*^H{\setminus } \{x\})\) and therefore, \(N(x) = L_r^H \cup (L_*^H{\setminus } \{x\})\) in \(G(T,\sigma )\) for all \(x\in L[r]\cap L_*^H\). By Property (C2.a), the latter is also satisfied in \((G,\sigma )\) for all \(x\in L[r]\cap L_*^H\). Hence, the respective neighborhoods of all \(x\in L[r]\cap L_*^H\) in \(G(T,\sigma )\) and \((G,\sigma )\) coincide.
Now let \(x\in L(T(v_1)) = L_t^H\). By construction and Lemma 19(i), we have \(xy\in E(G(T,\sigma ))\), resp., \(xy\in E(G)\) for \(y\in L[s]\) if and only if \(\mathsf {par} (x)=\mathsf {par} (y)\). Hence, the respective neighborhoods \(N_s(x)\) of all \(x\in L(T(v_1))\cap L[r]=L_t^H\cap L[r]\) in \(G(T,\sigma )\) and \((G,\sigma )\) coincide. Now consider the neighborhood \(N_t(x)\) in \(G(T,\sigma )\). Since \(r\in \sigma (L(T(v_2)))=L_s^H\), Lemma 19(ii) implies that x is not adjacent to any vertex in \(L_s^H\). Hence, as \(t\notin \sigma (L_t^H)\), if follows \(N_t(x)\subseteq L_*^H[t]\cup L_r^H[t]\). Since there is no leaf of color t in \(L(T(v_1))\), we have \(L_*^H[t]\subseteq N_t(x)\) by Lemma 19(iv). Moreover, since \(r\notin \sigma (L(T(v_3)))\), Lemma 19(ii) implies \(L_r^H[t]=L(T(v_3))\cap L[t]\subseteq N_t(x)\). Hence, \(L_*^H[t]\cup L_r^H[t] \subseteq N_t(x)\) and we therefore conclude \(N_t(x) = L_*^H[t]\cup L_r^H[t]\). By Property (C2.b), the latter is also satisfied in \((G,\sigma )\) for all \(x\in L(T(v_1)) = L_t^H\). Hence, the respective neighborhoods \(N_t(x)\) of all \(x\in L_t^H\cap L[r]\) are identical in \(G(T,\sigma )\) and \((G,\sigma )\). Since \(N_t(x)\cup N_s(x) = N(x)\), the neighborhoods N(x) coincide in \(G(T,\sigma )\) and \((G,\sigma )\) for every \(x\in L_t^H\cap L[r]\). By similar arguments, one can show that the same is true for any \(x\in L_s^H\cap L[r]\).
By symmetry, analogous arguments show that the neighborhoods of leaves with color s or t are the same in \((G,\sigma )\) and \(G(T,\sigma )\). We therefore conclude \((G,\sigma )=G(T,\sigma )\), i.e., \((T,\sigma )\) explains \((G,\sigma )\).
Conversely, let \((G,\sigma )\) be a connected, \({\mathsf {S} }\)-thin 3-RBMG of Type (C). By Theorem 4, \((G,\sigma )\) is either a hexagon, or \(|L|>6\) and it contains a hexagon H of the form (r, s, t, r, s, t). In the latter case, Lemma 26 implies that \((G,\sigma )\) is always C-like w.r.t. some hexagon \(H = \langle {\hat{x}}_1{\hat{y}}_1{\hat{z}}_1 {\hat{x}}_2 {\hat{y}}_2 {\hat{z}}_2 \rangle \) with \({\hat{x}}_i\in L[r]\), \({\hat{y}}_i\in L[s]\), \({\hat{z}}_i \in L[t]\). Similar arguments as in the proof of Lemma 26 show that w.l.o.g. we can assume \(|N_t({\hat{x}}_1)|>1\). Hence, \((G,\sigma )\) satisfies Property (C1). Moreover, Lemma 26 implies that there exists a tree \((T,\sigma )\) of Type (III) that explains \((G,\sigma )\) and such that \(L(T(v_1)) = L_t^H\), \(L(T(v_2)) = L_s^H\), \(L(T(v_3)) = L_r^H\) and \(L_*^H=\mathsf {child} (\rho _T)\cap L\). Now, careful application of Lemma 19(i)–(iv), which we leave to the reader, shows that Conditions (C2.a) to (C4.c) are satisfied. \(\square \)
If \((G,\sigma )\) is a 3-RBMG of Type (C), an analogous construction as in the case of Type (B) 3-RBMGs can be used to obtain \((G,\sigma )\) from the sets \(L_t^H\), \(L_s^H\), \(L_r^H\), and \(L_*^H\). Again, this information may be useful for correcting the orthology graph. If \(|L|=6\) then \((G,\sigma )\) is already a hexagon \(H = \langle x_1 y_1 z_1 x_2 y_2 z_2 \rangle \) such that, up to permutation of the colors, \(\sigma (x_i)=r\), \(\sigma (y_i)=s\), and \(\sigma (z_i)=t\), \(i\in \{1,2\}\). This 3-colored graph is explained by the two distinct trees \(T_1:=((x_1,y_1),(z_1,x_2),(y_2,z_2))\) and \(T_2:=((y_1,z_1),(x_2,y_2),(z_2,x_1))\), given in standard Newick tree format. These two trees induce different leaf sets \(L(T(v_i))\), where \(v_i\in \mathsf {child} (\rho _T)\cap V^0(T)\) in the corresponding tree. One can show, however, that for \(|L|>6\), every hexagon defines the same sets \(L_i^H\), \(i\in \{t,s,r\}\) and \(L_*^H\). To this end we will need the following technical result:
Lemma 28
Let \((T,\sigma )\) be a tree of Type (III) with root \(\rho _T\) explaining a connected \({\mathsf {S} }\)-thin 3-RBMG \((G,\sigma \)) and let \(H:=\langle {\hat{x}}_1 {\hat{y}}_1{\hat{z}}_1{\hat{x}}_2{\hat{y}}_2{\hat{z}}_2 \rangle \) be a hexagon in \((G,\sigma )\) such that \({\hat{x}}_i\in L[r]\), \({\hat{y}}_i\in L[s]\) and \({\hat{z}}_i\in L[t]\) for distinct colors r, s, t and \(1\le i\le 2\). Then, \({\hat{x}}_i, {\hat{y}}_i, {\hat{z}}_i \notin \mathsf {child} (\rho _T)\), \(1\le i\le 2\).
Proof
By definition of \((T,\sigma )\), there exist distinct \(v_1,v_2,v_3\in \mathsf {child} (\rho _T)\) such that \(\sigma (L(T(v_1)))=\{r,s\}\), \(\sigma (L(T(v_2)))=\{r,t\}\), and \(\sigma (L(T(v_3)))=\{s,t\}\), and \(\mathsf {child} (\rho _T){\setminus } \{v_1,v_2,v_3\} \subset L\). Assume, for contradiction, that \({\hat{x}}_1\in \mathsf {child} (\rho _T)\). Then, either \({\hat{y}}_1\in \mathsf {child} (\rho _T)\) or, by Lemma 19(iv), \({\hat{y}}_1\preceq _T v_3\). In the latter case, Lemma 19(i) implies \({\hat{z}}_1\preceq _T v_3\) and thus \({\hat{x}}_1{\hat{z}}_1\in E(G)\) by Lemma 19(iv); contradicting that H is a hexagon. Hence, \({\hat{x}}_1\notin \mathsf {child} (\rho _T)\). Due to symmetry, we can apply similar arguments to the remaining vertices \({\hat{x}}_2, {\hat{y}}_i, {\hat{z}}_i\), \(1\le i\le 2\), to show that none of them is contained in \(\mathsf {child} (\rho _T)\). \(\square \)
We are now in the position to prove the uniqueness of \(L_i^H\), \(i\in \{r,s,t\}\), and \(L_*^H\).
Lemma 29
Let \((G,\sigma )\) be a connected \({\mathsf {S} }\)-thin 3-RBMG of Type (C) with leaf set \(|L|>6\). Moreover, let the sets \(L_t^H\), \(L_s^H\), \(L_r^H\), and \(L_*^H\) be defined w.r.t. an induced hexagon \( H :=\langle {\hat{x}}_1{\hat{y}}_1{\hat{z}}_1{\hat{x}}_2{\hat{y}}_2{\hat{z}}_2 \rangle \) with \(|N_t({\hat{x}}_1)|>1\), where \({\hat{x}}_i\in L[r]\), \({\hat{y}}_i\in L[s]\) and \({\hat{z}}_i\in L[t]\) for distinct colors r, s, t. Then, for any hexagon \( H'\) of the form (r, s, t, r, s, t) we have \(L_t^{H'}=L_t^H\), \(L_s^{H'}=L_s^H\), \(L_r^{H'}=L_r^H\), and \(L_*^{H'}=L_*^H\).
Proof
Let \((T,\sigma )\) be a leaf-colored tree explaining \((G,\sigma )\), which, by Theorem 4 can be chosen to be of Type (III), i.e., there are distinct \(v_1,v_2,v_3\in \mathsf {child} (\rho _T)\) such that \(\sigma (L(T(v_1)))=\{r,s\}\), \(\sigma (L(T(v_2)))=\{r,t\}\), and \(\sigma (L(T(v_3)))=\{s,t\}\), and \(\mathsf {child} (\rho _T){\setminus } \{v_1, v_2, v_3\} \subset L\). In particular, Lemma 26 implies that \((T,\sigma )\) can be chosen such that \(L_t^H=L(T(v_1))\), \(L_s^H=L(T(v_2))\), \(L_r^H=L(T(v_3))\), and \(L_*^H=\mathsf {child} (\rho _T)\cap L\). Lemma 28 implies \(V(H)\cap \mathsf {child} (\rho _T)=\emptyset \). Since \({\hat{x}}_1\) has more than one neighbor of color t, Lemma 19(i) and \({\mathsf {S} }\)-thinness of \((G,\sigma )\) imply that \({\hat{x}}_1\) cannot be contained in \(L(T(v_2))\) as otherwise \(|N_t({\hat{x}}_1)|\le 1\). Hence, \({\hat{x}}_1\preceq v_1\). Applying Lemma 19(i)+(ii), we then conclude that \({\hat{y}}_1\preceq _T v_1\), \({\hat{x}}_2, {\hat{z}}_1\preceq _T v_2\), and \({\hat{y}}_2, {\hat{z}}_2\preceq _T v_3\). In other words, \({\hat{x}}_1,{\hat{y}}_1\in L_t^H\), \({\hat{x}}_2,{\hat{z}}_1\in L_s^H\), and \({\hat{y}}_2,{\hat{z}}_2\in L_r^H\).
We proceed to show that the leaf sets \(L_t^H\), \(L_s^H\), \(L_r^H\), and \(L_*^H\) remain unchanged if they are taken w.r.t. some other vertex \(v\in V(H){\setminus } \{{\hat{x}}_1\}\) with \(|N_c(v)|>1\) for some color \(c\ne \sigma (v)\). Note that, as \((G,\sigma )\) is explained by \((T,\sigma )\) and \({\hat{x}}_1\in L_t^H\), we can apply Property (C2.b) to conclude \(|N_s({\hat{x}}_1)|\le 1\). Suppose first \(v={\hat{y}}_1\) and \(|N_c({\hat{y}}_1)|>1\). Since \({\hat{y}}_1\in L_t^H\), we can apply Property (C3.b) and obtain \(|N_r({\hat{y}}_1)|\le 1\). Hence we have \(c=t\). The definition of \(L_t\) with \(v={\hat{y}}_1\) and \(c=t\) implies that \(L_t^{H'}=\{y\mid \langle y{\hat{z}}_1 {\hat{x}}_2\rangle \in {\mathcal {P}}_3\}\cup \{x\mid \langle x{\hat{z}}_2 {\hat{y}}_2\rangle \in {\mathcal {P}}_3\}=L_t^H\). Similarly, one obtains \(L_s^{H'}=L_s^H\) and \(L_r^{H'}=L_r^H\). Now, let \(v={\hat{z}}_1\) and \(|N_c({\hat{z}}_1)|>1\). Then, as \((T,\sigma )\) explains \((G,\sigma )\) and \({\hat{z}}_1\in L_s^H\), Property (C4.b) implies \(|N_r({\hat{z}}_1)|\le 1\). Hence \(c=s\).
Again, the definition of \(L_t^H\) with \(v={\hat{z}}_1\) and \(c=s\) implies that \(L_t^{H'}=L_t^H\). Similarly, the definition of \(L_s^H\) and \(L_r^H\) with \(v={\hat{z}}_1\) and \(c=s\) shows that \(L_s^{H'}=L_s^H\), and \(L_r^{H'}=L_r^H\). Applying similar arguments to \(v={\hat{y}}_2\), \(v={\hat{z}}_2\) and \(v={\hat{x}}_2\) under the assumption that \(|N_c(v)|>1\) for some color \(c\ne \sigma (v)\), shows that v and c always induce the same leaf sets \(L_t^H\), \(L_s^H\), \(L_r^H\). The latter implies that also the set \(L_*^H\) is independent from the particular choice of the vertices v in H.
Now let \(H':=\langle x_1 y_1 z_1 x_2 y_2 z_2\rangle \ne H\) with \(x_i\in L[r]\), \(y_i\in L[s]\), \(z_i\in L[t]\). Lemma 28 implies that \(x_1\) and \(x_2\) are not incident to the root of \((T,\sigma )\), hence \(x_1,x_2\in L(T(v_1))\cup L(T(v_2))\). Assume, for contradiction, that they are contained in the same subtree, say \(x_1,x_2\in L(T(v_1))\). Then, as \(x_2z_1\in E(G)\) and \(\sigma (L(T(v_1)))=\{r,s\}\), Lemma 19(ii) implies that \(z_1\) cannot reside within a subtree that contains leaves of color r, thus \(z_1\in L(T(v_3))\). Therefore, we can again apply Lemma 19(ii) to conclude that \(x_1z_1\in E(G)\); a contradiction since \(H'\) is a hexagon. Analogously one shows that \(x_1\) and \(x_2\) cannot be both located in the subtree \(T(v_2)\). Hence, we can w.l.o.g. assume \(x_1\in L(T(v_1))\). Then, by construction of \((T,\sigma )\), we have \({{\,\mathrm{lca}\,}}_T(x_1,z)={{\,\mathrm{lca}\,}}_T({\hat{x}}_1,z)\) for any \(z\in L[t]\), thus \(N_t(x_1)=N_t({\hat{x}}_1)\) and in particular \(|N_t(x_1)|>1\). Applying Lemma 28 and analogous argumentation as for H yields \(x_1, y_1\preceq _T v_1\), \(x_2, z_1\preceq _T v_2\), and \(y_2, z_2\preceq _T v_3\). Thus, In other words, \( x_1, y_1\in L_t^H\), \( x_2, z_1\in L_s^H\), and \( y_2, z_2\in L_r^H\).
Consider first \(L_t^H\) and let \(x\in L[r]\). By definition, \(x\in L_t^H\) if and only if \(\langle x{\hat{z}}_2{\hat{y}}_2\rangle \) is an induced \(P_3\). Since \(\sigma (L(T(v_1)))=\{r,s\}\) and \(\sigma (L(T(v_3)))=\{s,t\}\), Lemma 19(ii) implies \(\langle x z_2 y_2\rangle \in {\mathcal {P}}_3\), i.e., \(x\in L_t^{H'}\). Conversely, suppose \(x\in L_t^{H'}\), thus \(\langle x z_2 y_2\rangle \in {\mathcal {P}}_3\). Since \((T,\sigma )\) explains \((G,\sigma )\) and \(y_2, z_2\preceq _T v_3\), Lemma 19(ii)+(iv) implies \(x\in L(T(v_1))=L_t^H\). Hence, \(L_t^H\cap L[r]=L_t^{H'}\cap L[r]\). Similar arguments show \(L_t^H\cap L[s]=L_t^{H'}\cap L[s]\) and thus \(L_t^H=L_t^{H'}\). By symmetry, analogous arguments yield \(L_s^H=L_s^{H'}\) and \(L_r^H=L_r^{H'}\). Taken together, this implies \(L_*^H=L_*^{H'}\). Analogous argumentation as used for H shows that any vertex \(v\in V(H')\) with \(|N_c(v)|>1\), \(c\ne \sigma (v)\), induces the same leaf sets \(L_t^{H'}\), \(L_s^{H'}\), \(L_r^{H'}\), and \(L_*^{H'}\), which finally completes the proof. \(\square \)
In contrast to Observation 4 for Type (B) 3-RBMGs, we obtain the following result.
Corollary 7
Let \((G,\sigma )\) be a connected \({\mathsf {S} }\)-thin 3-RBMG of Type (C). If \((G,\sigma )\) is C-like w.r.t. a hexagon H, then \((G,\sigma )\) is C-like w.r.t. every hexagon of the form (r, s, t, r, s, t).
1.6 Characterization of 3-RBMGs and algorithmic results
For later reference, finally, we summarize the main results of this section, i.e., Theorem 4 and the characterizations of the three types in Lemmas 22, 25, and 27:
Theorem 6
An undirected, connected, properly 3-colored, \({\mathsf {S} }\)-thin graph \((G,\sigma )\) is a 3-RBMG if and only if it satisfies either conditions (A1) and (A2), (B1)–(B3.b), or (C1)–(C3.c) and thus, is of Type (A), (B), or (C).
Proof
By Theorem 4, any \({\mathsf {S} }\)-thin connected 3-RBMG \((G,\sigma )\) must be either of Type (A), (B), or (C). Lemma 22 implies that \((G,\sigma )\) is a 3-RBMG of Type (A) if and only if it satisfies (A1) and (A2). By Lemma 25, \((G,\sigma )\) is a 3-RBMG of Type (B) if and only if Properties (B1)–(B4.b) are satisfied. However, as the neighborhoods of all vertices of one color can clearly be recovered from the neighborhoods of all vertices of different color, Properties (B4.a) and (B4.b) are redundant, i.e., \((G,\sigma )\) is a Type (B) 3-RBMG if and only if (B1) to (B3.b) are satisfied. One analogously argues that Properties (C4.a)–(C4.c) are redundant. \(\square \)

Let us now consider the question how difficult it is to decide whether a given graph is a 3-RBMG or not. It easy to see that all conditions in Theorem 6 can be tested in polynomial time. In case \((G,\sigma )\) is a 3-RBMG, we are also interested in a tree that can explain \((G,\sigma )\). Unless \((G,\sigma )\) is of Type (A), we have we have to construct the leaf sets \(L_s^P\), \(L_t^P\), \(L_*^P\), or \(L_s^H\), \(L_t^H\), \(L_r^H\), \(L_*^H\), respectively. Instead of checking each of the conditions for Type (B) or Type (C) graphs in Theorem 6, we can directly construct the tree \((T,\sigma )\) directly from the sets \(L_i^X\), \(i\in \{r,s,t\}\), \(X\in \{P,H\}\) (cf. Lemma 24, resp., 26) and test whether or not \((T,\sigma )\) explains \((G,\sigma )\). The overall structure of this algorithm is summarized in Algorithm 1. We first show in Lemma 30 that Algorithm 1 indeed recognizes 3-RBMGs and, in the positive case, returns a tree. The proof of Lemma 30 provides at the same time a description of the single steps of Algorithm 1. We then continue to show in Lemma 31 that Algorithm 1 runs in \( O(|V(G/{\mathsf {S} })|^2 |E(G/{\mathsf {S} })| + |E(G)|)\) time for a given input graph \((G,\sigma )\).
Lemma 30
Algorithm 1 determines if a given properly 3-colored connected graph \((G',\sigma ')\) is a 3-RBMG and, in the positive case, returns a tree \((T',\sigma ')\) that explains \((G',\sigma ')\)
Proof
Given a properly 3-colored connected graph \((G',\sigma ')\), we first compute \((G,\sigma ) = (G'/{\mathsf {S} }, \sigma _{/{\mathsf {S} }}')\). By construction, \((G,\sigma )\) remains properly 3-colored and, by Lemma 5, \((G,\sigma )\) is \({\mathsf {S} }\)-thin and connected.
In Line 2, if \((G,\sigma )\) is of Type (A), then we can compute the tree \((T,\sigma )\) that explains \((G,\sigma )\) as constructed for the “if-direction” in the proof of Lemma 22, and jump to Line 18.
If \((G,\sigma )\) is not of Type (A), then we proceed by testing if \((G,\sigma )\) is of Type (C). To this end, we search first for one hexagon H of the form (r, s, t, r, s, t) in Line 6. If such a hexagon H exists, we check if \((G,\sigma )\) is C-like w.r.t. H. By Corollary 7, it is indeed sufficient to test C-likeness for one hexagon only. If \((G,\sigma )\) is C-like w.r.t. H, then we compute the sets \(L_t^H\), \(L_s^H\), \(L_r^H\), \(L_*^H\) (Line 8). We proceed in Line 9 to construct a tree \((T,\sigma )\) based on the set \(L_t^H\), \(L_s^H\), \(L_r^H\), \(L_*^H\) according to Lemma 26. Now, to test if \((G,\sigma )\) is of Type (C), we can again apply Lemma 26 which implies that it suffices show that \((T,\sigma )\) explains \((G,\sigma )\). If this is the case, we again jump to Line 18 and, if not, we proceed to check if \((G,\sigma )\) is of Type (B).
If \((G,\sigma )\) is neither of Type (A) nor (C), then either \((G,\sigma )\) is not a 3-RBMG or it must be of Type (B). Thus, we continue in Line 12–15 to test if \((G,\sigma )\) can be explained by some tree \((T,\sigma )\). To this end, Observation 4 implies that we must check for every \(P\in {\mathcal {P}}_4\) (for which the two endpoints have the same color), whether \((G,\sigma )\) satisfies Definition 15(i). If this is not the case for any such induced \(P_4\), then Lemma 24 implies that \((G,\sigma )\) is not of Type (B). Together with the preceding tests, we can conclude that \((G,\sigma )\) is not a 3-RBMG. Hence, the algorithm stops in Line 17 and returns “\((G,\sigma )\) is not a 3-RBMG”. Otherwise, if \((G,\sigma )\) satisfies Definition 15(i) w.r.t. P, we construct a tree \((T,\sigma )\) based on the set \(L_s^P\), \(L_t^P\), \(L_*^P\) according to Lemma 24. Again by Lemma 24, it is now sufficient to show that \((T,\sigma )\) explains \((G,\sigma )\) in order to test if \((G,\sigma )\) is a 3-RBMG. Since the preceding tests already have established that \((G,\sigma )\) is neither of Type (A) nor (C), we can conclude that \((G,\sigma )\) is of Type (B). If \((G,\sigma )\) is a 3-RBMG, then we jump to Line 18, otherwise we stop again in Line 17 and the algorithm returns “\((G,\sigma )\) is not a 3-RBMG”.
Finally, after having verified that \((G,\sigma )\) is indeed a 3-RBMG and constructed \((T,\sigma )\), the algorithm reaches Line 18. Lemma 7 implies that \((G',\sigma ')\) is a 3-RBMG. Moreover, the construction in the last part of the proof of Lemma 7 shows how to obtain a tree \((T',\sigma ')\) that explains \((G',\sigma ')\) from \((T,\sigma )\). In Line 19, the respective trees \((T',\sigma ')\) and \((T,\sigma )\) are returned. \(\square \)
Lemma 31
Let \((G',\sigma ')\) is an undirected, properly 3-colored, connected graph and let \(n=|V(G'/{\mathsf {S} })|\), \(m=|E(G'/{\mathsf {S} })|\) and \(m'= |E(G')|\). Algorithm 1 processes \((G',\sigma ')\) in \(O(mn^2+m')\) time.
Proof
In a worst case, Observation 4 implies that we need to list all induced \(P_4\)s \(\langle {\hat{x}}_1 {\hat{y}} {\hat{z}} {\hat{x}}_2 \rangle \) with \(\sigma ({\hat{x}}_1) = \sigma ({\hat{x}}_2)\). Since for any edge yz in G, there exist at most \((n-2)(n-3)\) possible combinations of vertices x and \(x'\) such that \(\langle xyzx'\rangle \) forms an induced \(P_4\), there are at most \(O(mn^2)\) such paths. Hence, the global runtime of the algorithm cannot be better than \(O(mn^2)\). Thus, we only provide rough upper bounds for all other subtask to show that they stay within \(O(mn^2)\) time.
The computation of the relation \({\mathsf {S} }\), its equivalence classes and \((G=(V,E),\sigma ) = (G'/{\mathsf {S} }, \sigma _{/{\mathsf {S} }}')\) in Line 1 can be done in a similar fashion as outlined by Hammack et al. (2011, Section 24.4) in \(O(|E(G')|)\) time, cf. (Hammack et al. 2011, Lemma 24.10).
To test whether \((G,\sigma )\) is of Type (A), we first apply Corollary 6 and check for which colors \(i\in \{r,s,t\}\) we have \(|L[i]|=1\), which can be done in O(n) time. We then apply Lemma 22 and verify if \(G\notin {\mathcal {P}}_3\). Note that the latter task can be done in constant time, since we can check if \(n=3\) and, in the positive case, if the three vertices of G are pairwisely connected by an edge in constant time O(1). We apply Lemma 22 again, and check for all colors \(i\in \{r,s,t\}\) with \(L[i]=\{x\}\), if x is a hub-vertex and if \(|N(y)|<3\) for every \(y\in V{\setminus } \{x\}\). Both of the latter tasks can be done in O(n) time. If such a color and vertex exists, then \((G,\sigma )\) is of Type (A) and we can build the tree \((T,\sigma )\) that explains \((G,\sigma )\). To this end, we apply the construction as in the “if-direction” of the proof of Lemma 22. We first construct the caterpillar \((T_2 , \sigma _{|L_2})\) with leaf set \(L_2 = \{y\mid y\ne x, |N(y)|=2\}\) and root \(\rho _{T_2}\). It is easy to see that \(L_2\) can be constructed in O(n) time. For the tree \(T_2\) we add vertices such that \(\mathsf {par} (y) = \mathsf {par} (z)\) for any \(y,z \in L_2\) with \(\sigma (y) \ne \sigma (z)\) if and only if \(yz \in E(G)\). Clearly, this task can be done in O(m) time. To construct the final tree \((T,\sigma )\) we need to check if \(|V{\setminus } L_2|=2\) or \(|V{\setminus } L_2|=3\), which can be done trivially in \(O(n^2)\) time. All remaining steps to construct \((T,\sigma )\) can be done in constant time. Hence, to construct \((T,\sigma )\) we need \(O(m+n^2)=O(n^2)\) time. In summary, Lines 2 and 3 have overall time complexity \(O(n^2)\).
We continue by testing if \((G,\sigma )\) is of Type (C) in Line 6–10. In Line 6, we first check if \((G,\sigma )\) is C-like w.r.t. some hexagon H. Note, all candidate hexagons must be of the form (r, s, t, r, s, t). In order to find such hexagons, we first compute the pairwise distances between all vertices in \(O(n^3)\subseteq O(n^2m)\) time (Floyd-Warshall). Then, we fix one of the colors, say r. Clearly, two vertices in L[r] that have distance larger or smaller than 3, cannot be both located on such a hexagon. Thus, for all vertices \(x,x'\in L[r]\) with distance \(d(x,x')=3\) we proceed as follows: We check for all edges yz with \(y\in L[s]\), \(z\in L[t]\), if \(x\in N_r(y)\), \(x'\in N_r(z)\), \(x'\notin N_r(y)\), \(x \notin N_r(z)\). If this is the case, \(\langle xyzx' \rangle \in {\mathcal {P}}_4\) and we store \(\langle xyzx' \rangle \) in the list \(P_{(x,x')}[s,t]\). Similarly, if for the edge yz with \(y\in L[s]\), \(z\in L[t]\) we have \(x\in N_r(z)\), \(x'\in N_r(y)\), \(x'\notin N_r(z)\), \(x \notin N_r(y)\), then we put \(\langle xzyx' \rangle \) in the list \(P_{(x,x')}[t,s]\). For each edge, the latter tests can be done in constant time, e.g. by using the adjacency matrix representation of \((G, \sigma )\). As soon as we have found two vertices \(x,x'\in L[r]\) such that each list \(P_{(x,x')}[s,t]\) and \(P_{(x,x')}[t,s]\) contains at least one element \(\langle xyzx' \rangle \) and \(\langle xz'y'x' \rangle \) such that \(yz'\) and \(zy'\) do not form an edge, we have found a hexagon \(H=\langle xyzx'y'z' \rangle \) of the form (r, s, t, r, s, t). Thus, for a given pair \(x,x'\in L[r]\), finding a hexagon that contains x and \(x'\) can be done in O(m) time. As the latter may be repeated for all \(x,x'\in L[r]\), we can conclude that finding a hexagon of the form (r, s, t, r, s, t) in Line 6, can be done \(O(|L[r]|^2 m) = O(n^2 m)\) time. Clearly, the test if \((G,\sigma )\) is C-like w.r.t. H in Line 7 can be done in constant time. Now, the sets \(L_s^H\), \(L_t^H\), \(L_r^H\), \(L_*^H\) are computed in Line 8. To determine these sets, we compute for each edge uv in H all vertices \(w\in V{\setminus } (L[\sigma (u)]\cup L[\sigma (v)])\) such that \(\langle wuv \rangle \in {\mathcal {P}}_3\). The latter can be done in O(n) for each edge in H. Since H has only a constant number of edges, all sets \(L_s^H\), \(L_t^H\), \(L_r^H\) can be constructed in O(n) time. The set \(L_*^H\) can then be trivially constructed in \(O(n^2)\) time. Now, we continue in Line 9 to construct a tree \((T,\sigma )\) as in Lemma 26. Similar arguments as in the Type (A) case show that \((T,\sigma )\) can be constructed in O(m) time. Finally, we check in Line 10 if \((T,\sigma )\) explains \((G,\sigma )\). To this end, we note that T has O(n) vertices. Moreover it was shown in (Schieber and Vishkin 1988), that the last common ancestor of x and y can be accessed in constant time, after an \(O(|V(T)|) = O(n)\) time preprocessing step. Hence, for each edge \(xy\in E(G)\), we check if \({{\,\mathrm{lca}\,}}(x,y) \preceq _T {{\,\mathrm{lca}\,}}(x,y')\) and \({{\,\mathrm{lca}\,}}(x,y) \preceq _T {{\,\mathrm{lca}\,}}(x',y)\) for all \(x'\in L[\sigma (x)]\) and \(y'\in L[\sigma (y)]\) in \(O(n^2)\). As this has to repeated for all edges of G, Line 10 takes \(O(mn^2)\) time. In summary, testing if \((G,\sigma )\) is of Type (C) in Line 6–10 can be done in \(O(mn^2)\) time.
In Line 12, we verify if \((G,\sigma )\) satisfies Definition 15(i) w.r.t. some \(P\in {\mathcal {P}}_4\). Note, there are at most \(mn^2\)\(P_4\)s \(\langle abcd\rangle \) with \(\sigma (a) = \sigma (d)\) in \((G,\sigma )\). Listing all such induced \(P_4\)s can therefore trivially be done \(O(mn^2)\) time. For each induced \(P_4\)\(\langle abcd\rangle \) with \(\sigma (a)=\sigma (d)\) we can verify the condition in Definition 15(i) in at most O(n) time. Thus, Line 12 requires \(O(mn^2)\) time.
In Line 13, we need to construct the sets \(L_s^P\), \(L_t^P\), and \(L_*^P\). Assume that \(P = \langle {\hat{x}}_1 {\hat{y}} {\hat{z}} {\hat{x}}_2 \rangle \) is of the form (r, s, t, r). To construct the set \(L_{t,s}^P\), we have \(y\in L_{t,s}^P\) if the edge \(y{\hat{z}}\) and every \(x\in N_r(y)\) form an induced \(P_3\). For each edge \(y{\hat{z}}\) the latter can be tested in O(n) time. To obtain \(L_{t,s}^P\) the latter test must be repeated for all edges \(y{\hat{z}}\) with \(y\in L[s]\). Thus, \(L_{t,s}^P\) can be constructed in O(mn) time. The set \(L_{t,r}^P\) is the disjoint union of two sets \(L'\) and \(L''\), where the first set \(L'\) contains all \(x\in L[r]\) for which \(x,y,{\hat{z}}\) induce a \(P_3\) with \(N_r(y)=\{x\}\) and the second set \(L''\) contains all \(x\in L[r]\) with \(N_s(x)=\emptyset \) whenever \(L[s]{\setminus } L_{t,s}^P\ne \emptyset \). By similar arguments as for \(L_{t,s}^P\), the set \(L'\) can be constructed in O(mn) time. For the set \(L''\), observe that \(L[s]{\setminus } L_{t,s}^P\ne \emptyset \) can be trivially verified in at most \(O(n^2)\) time and \(N_s(x)=\emptyset \) can be verified in O(n) time for a given \(x\in L[r]\). To obtain \(L''\) we must repeat the latter for all \(x\in L[r]\) and hence, end up with a time complexity \(O(n^3) \subseteq O(n^2m)\). In summary, the set \(L_{t,s}^P\) and \(L_{t,r}^P\) can be constructed in O(mn) and \(O(n^2m)\) time, respectively. Therefore, \(L_t^P\) can be constructed in \(O(n^2m)\) time. By symmetry, the construction of \(L_s^P\) can be done in \(O(n^2m)\) time as well. The set \(L_*^P = V{\setminus } (L_t^P\cup L_s^P)\) can then trivially be constructed in \(O(n^2)\) time. Now, we continue in Line 14 to construct a tree \((T,\sigma )\) as in Lemma 24. Similar arguments as in the Type (A) case show that \((T,\sigma )\) can be constructed in O(m) time. Finally, we check in Line 15 if \((T,\sigma )\) explains \((G,\sigma )\). By similar arguments as in the Type (C) case, the latter task can be done in \(O(mn^2)\) time. In summary, Lines 12–15 require \(O(mn^2)\) time.
Finally we construct, in Line 18 the tree \((T',\sigma ')\) for \((G',\sigma ')\) based on the tree \((T,\sigma )\). Given the equivalence classes as computed in the first step (Line 1), one can construct \((T',\sigma ')\) as in the last part of the proof of Lemma 7. Thus, for each of the n leaves x we can check in O(n) time in which class it is contained and then expand the leaf x by |[x]| vertices. As there are at most \(O(n')\) vertices that we may additionally add to \((T,\sigma )\), we can construct \((T',\sigma ')\) in \(O(n+n')=O(n')\subseteq O(m')\) time. Since the task of computing the quotient graph \((G,\sigma )\) already takes \(O(m')\) time, we end up with an overall runtime of \(O(mn^2 + m')\). \(\square \)
The good, the bad, and the ugly: induced \(P_4\)s
In order to gain a better understanding of Type (B) 3-RBMGs, we consider here in more detail the influence of the choice of the “reference” \(P_4\) on the definition of the vertex sets \(L_t^P\), \(L_s^P\), and \(L_*^P\) that determine the structure of \((G,\sigma )\). The \(P_4\)s can be classified as so-called good, bad, and ugly quartets. Quartets will play an essential role for the characterization of 3-RBMGs as we shall see later. In particular, the sets \(L_t^P\), \(L_s^P\), and \(L_*^P\) can be determined by good quartets and are independent of the choice of the respective good quartet. As shown by Geiß et al. (2019b), good quartets also play an important role for the detection of false positive and false negative orthology assignments.
Observation 5
An n-RBMG does not contain an induced \(P_4\) with two colors. Moreover, any induced \(P_4\) with three distinct colors is either of the Type \(\langle xyzx'\rangle \) or \(\langle xyx'z\rangle \) with \(\sigma (x)=\sigma (x')\).
Proof
As shown by Geiß et al. (2019a, Cor. 6), there is no induced \(P_4\) with only two colors since all 2-RBMGs are complete bipartite graphs. Hence, if we have three distinct colors, then exactly two vertices have the same color. Since RBMGs are properly colored, these vertices cannot be adjacent, leaving only the two alternatives \(\langle xyzx'\rangle \) and \(\langle xyx'z\rangle \). \(\square \)
We emphasize that an RBMG on more than three colors may also contain induced \(P_4\)s with four distinct colors. Consider, for instance, the tree \(((a_1,b_1,c),(a_2,b_2,d))\), given in Newick format, where \(\sigma (a_i)=A\), \(\sigma (b_i)=B\), \(\sigma (c)=C\), and \(\sigma (d)=D\), \(i\in \{1,2\}\) where A, B, C, and D are pairwise distinct colors. Then the RBMG \(G(T,\sigma )\) contains the 4-colored induced \(P_4\)\(\langle a_1 c d b_2\rangle \). A characterization for n-RBMGs that are cographs will be given later in Theorem 8. For now we will restrict our attention to \(P_4\)s with three colors only.
Definition 17
(good, bad and ugly quartetsFootnote 2) Let \((\vec {G},\sigma )\) be a BMG with symmetric part \((G,\sigma )\) and let \(Q:=\{x,x',y,z\} \subseteq L\) with \(x,x'\in L[r]\), \(y\in L[s]\), and \(z\in L[t]\). The set Q, resp., the induced subgraph \(\vec {G}[Q],\sigma _{|Q})\) is
a good quartet if (i) \(\langle xyzx'\rangle \) is an induced \(P_4\) in \((G,\sigma )\) and (ii) \((x,z),(x',y)\in E(\vec {G})\) and \((z,x),(y,x')\notin E(\vec {G})\),
a bad quartet if (i) \(\langle xyzx'\rangle \) is an induced \(P_4\) in \((G,\sigma )\) and (ii) \((z,x),(y,x')\in E(\vec {G})\) and \((x,z),(x',y)\notin E(\vec {G})\),
an ugly quartet if \(\langle xyx'z\rangle \) is an induced \(P_4\) in \((G,\sigma )\).
Figure 13 shows an example of an RBMG containing a good quartet. Note that good, bad, and ugly quartets cannot appear in RBMGs whose induced 3-colored subgraphs are all Type (A) 3-RBMGs: by definition, these do not contain induced \(P_4\)s.
The \({\mathsf {S} }\)-thin 3-RBMG \((G,\sigma )\) is explained by two trees \((T_1,\sigma )\) and \((T_2,\sigma )\) that induce distinct BMGs \(\vec {G}(T_1,\sigma )\) and \(\vec {G}(T_2,\sigma )\). In \(\vec {G}(T_1,\sigma )\), \(P^1 =\langle a_1b_1c_1a_2\rangle \) defines a good quartet, while \(P^2 =\langle a_1c_2b_2a_2\rangle \) induces a bad quartet. In \(\vec {G}(T_2,\sigma )\) the situation is reversed. Moreover, the quartets for \(P^1\) and \(P^2\) induce different leaf sets. Denoting the leaf colors “red”, “blue”, and “green” by r, s, and t, respectively, we obtain \(L_t^{P^1}=\{a_1,b_1\}\), \(L_s^{P^1}=\{a_2,c_1\}\), and \(L_*^{P^1}=\{b_2,c_2\}\), while \(L_s^{P^2}=\{a_1,c_2\}\), \(L_t^{P^2}=\{a_2,b_2\}\), and \(L_*^{P^2}=\{b_1.c_1\}\). The good quartets in \(\vec {G}(T_1,\sigma )\) and \(\vec {G}(T_2,\sigma )\) are indicated by red edges. The induced paths \(\langle a_1 b_1 c_1 b_2\rangle \) and \(\langle a_2 c_1 b_1 c_2\rangle \) are examples of ugly quartets (color figure online)
Lemma 32
Let \((G,\sigma )\) be an RBMG, Q a set of four vertices with three colors, \(G[Q]\in {\mathcal {P}}_4\), and \((\vec {G},\sigma )\) a BMG containing \((G,\sigma )\). Then Q is either a good, a bad, or an ugly quartet.
Proof
By Observation 5, any induced \(P_4\) is either of the form \(\langle xyx'z\rangle \) or \(\langle xyzx'\rangle \). In the first case Q is an ugly quartet. For the remainder of the proof we thus assume \(\langle xyzx'\rangle \), and w.l.o.g, we suppose that the vertex colors are \(\sigma (x)=\sigma (x')=r\), \(\sigma (y)=s\), and \(\sigma (z)=t\).
Let \((T,\sigma )\) be a leaf-colored tree that explains \((\vec {G},\sigma )\), and thus, by assumption, also \((G,\sigma )\). Since \(\langle xyzx'\rangle \) is an induced \(P_4\) in \((G,\sigma )\), the edge xz cannot be contained in E(G). Hence, we are left with three cases: (i) \((x,z)\in E(\vec {G})\) and \((z,x)\notin E(\vec {G})\), (ii) \((z,x)\in E(\vec {G})\) and \((x,z)\notin E(\vec {G})\), and (iii) \((x,z),(z,x)\notin E(\vec {G})\).
Case (i) We have \(x'\in N^+_{r}(z)\) and \(x\notin N^+_{r}(z)\), i.e., \({{\,\mathrm{lca}\,}}_T(x',z)\prec _T{{\,\mathrm{lca}\,}}_T(x,z)=:u\). This implies \({{\,\mathrm{lca}\,}}_T(x,x')=u\). Moreover, \((x,y)\in E(G)\) implies \({{\,\mathrm{lca}\,}}_T(x,y)\preceq _T {{\,\mathrm{lca}\,}}_T(x',y)\). In case of equality, we have \({{\,\mathrm{lca}\,}}_T(x,y)= {{\,\mathrm{lca}\,}}_T(x',y)\succeq _T u\). Thus, \(x\in N^+_r(y)\) implies \(x'\in N^+_r(y)\). Hence, since \(x'y\notin E(G)\), there must exist a leaf \(y'\in L[s]\) such that \({{\,\mathrm{lca}\,}}_T(x',y')\prec _T {{\,\mathrm{lca}\,}}_T(x',y)\). Then, \({{\,\mathrm{lca}\,}}_T(x',z) \prec _T u\) implies either \({{\,\mathrm{lca}\,}}_T(z,y')\prec _T u \preceq _T {{\,\mathrm{lca}\,}}_T(x',y)\) or \({{\,\mathrm{lca}\,}}_T(z,y')={{\,\mathrm{lca}\,}}_T(x',y')\prec _T {{\,\mathrm{lca}\,}}_T(x',y)\). Either alternative contradicts \(yz\in E(G)\). Therefore, \({{\,\mathrm{lca}\,}}_T(x,y)\prec _T {{\,\mathrm{lca}\,}}_T(x',y)\). Together with \({{\,\mathrm{lca}\,}}_T(x,x')=u\) this implies \({{\,\mathrm{lca}\,}}_T(x,y)\prec _T u\). Now let \(u_y \succeq _T {{\,\mathrm{lca}\,}}_T(x,y)\) and \(u_z\succeq _T {{\,\mathrm{lca}\,}}_T(x',z)\), where \(u_y, u_z \in \mathsf {child} (u)\). Then, \(yz\in E(G)\) implies that \(t\notin \sigma (L(T(u_y)))\) and \(s\notin \sigma (L(T(u_z)))\). Hence, \((x,z),(x',y)\in E(\vec {G})\) and \((z,x),(y,x')\notin E(\vec {G})\), i.e., \(\{x,y,z,x'\}\) forms a good quartet.
Case (ii) We have \(x,x'\in N^+_r(z)\), thus \(u:={{\,\mathrm{lca}\,}}_T(x,z)={{\,\mathrm{lca}\,}}_T(x',z)\). On the other hand, \((x,z)\notin E(\vec {G})\) implies that there exists a leaf \(z'\in L[t]\) such that \({{\,\mathrm{lca}\,}}_T(x,z')\prec _T{{\,\mathrm{lca}\,}}_T(x,z)\). Hence, as \(z\in N^+_t(x')\), we have distinct \(u_x, u_{x'}, u_z \in \mathsf {child} (u)\) such that \(x,z' \prec _T u_x\), \(x' \preceq _T u_{x'}\), and \(z\preceq _T u_z\). Moreover, \(yz\in E(G)\) implies \({{\,\mathrm{lca}\,}}_T(y,z) \preceq _T {{\,\mathrm{lca}\,}}_T(y,z')\), thus we either have (a) \({{\,\mathrm{lca}\,}}_T(y,z) \prec _T {{\,\mathrm{lca}\,}}_T(y,z')\) or (b) \({{\,\mathrm{lca}\,}}_T(y,z) = {{\,\mathrm{lca}\,}}_T(y,z')\). In both cases, we have \(u_x\prec _T {{\,\mathrm{lca}\,}}(x,y)\), thus, since \(xy\in E(G)\), it follows \(s\notin \sigma (L(T(u_x)))\). Similarly, since \(zx'\in E(G)\), we have \(r\notin \sigma (L(T(u_z)))\) and \(t\notin \sigma (L(T(u_{x'})))\). This in particular implies \({{\,\mathrm{lca}\,}}(x',y)\preceq {{\,\mathrm{lca}\,}}(x,y)\). Moreover, since \(x'y\notin E(G)\), there must exist a leaf \(y'\in L[s]\) with \({{\,\mathrm{lca}\,}}_T(x',y')\prec _T {{\,\mathrm{lca}\,}}_T(x',y)\). In Case (a), we have \(y\in L(T(v_z))\) and thus \({{\,\mathrm{lca}\,}}_T(x',y)=u\), which implies \(y'\preceq _T u_{x'}\). In summary, this implies for Case (a) \(x,z'\prec _T u_x\), \(x',y'\prec _T u_{x'}\), and \(y,z\prec _T u_z\) as well as \(\sigma (L(T(u_x)))=\{r,t\}\), \(\sigma (L(T(u_{x'})))=\{r,s\}\), and \(\sigma (L(T(u_z)))=\{s,t\}\). Hence, \((z,x),(y,x')\in E(\vec {G})\) and \((x,z),(x',y)\notin E(\vec {G})\), i.e., \(\{x,y,z,x'\}\) is a bad quartet in \((\vec {G},\sigma )\). In Case (b), if \({{\,\mathrm{lca}\,}}_T(x',y')\succeq u\), then \({{\,\mathrm{lca}\,}}_T(x,y')={{\,\mathrm{lca}\,}}_T(x',y')\prec _T {{\,\mathrm{lca}\,}}_T(x',y)\), contradicting \(xy\in E(G)\). Hence, \(y'\preceq _T u_{x'}\). This implies \({{\,\mathrm{lca}\,}}_T(x,y)=u\) since otherwise \({{\,\mathrm{lca}\,}}_T(x,y')=u\prec _T {{\,\mathrm{lca}\,}}_T(x,y)\); again a contradiction to \(xy\in E(G)\). Let \(u_y\in \mathsf {child} (u)\) be such that \(y\preceq _T u_y\). Since \(xy, yz \in E(G)\), we conclude \(\sigma (L(T(u_y)))=\{s\}\). Moreover, \(yz\in E(G)\) then implies \(s\notin \sigma (L(T(u_z)))\). Summarizing Case (b), we thus have \(x,z'\prec _T u_x\), \(x',y'\prec _T u_{x'}\), \(y\preceq _T u_y\), and \(z\prec _T u_z\) as well as \(\sigma (L(T(u_x)))=\{r,t\}\), \(\sigma (L(T(u_{x'})))=\{r,s\}\), \(\sigma (L(T(u_y)))=\{s\}\), and \(\sigma (L(T(u_z)))=\{t\}\). One now easily checks that \(\{x,y,z,x'\}\) again forms a bad quartet in \((\vec {G},\sigma )\).
Case (iii) Let \(u:={{\,\mathrm{lca}\,}}_T(x,x')\). Then \((x,z),(z,x)\notin E(\vec {G})\) implies \({{\,\mathrm{lca}\,}}_T(x',z)\prec _T {{\,\mathrm{lca}\,}}_T(x,z)\) and there must exist some leaf \(z'\in L[t]\) such that \({{\,\mathrm{lca}\,}}_T(x,z')\prec _T {{\,\mathrm{lca}\,}}_T(x,z)\). Hence, there are \(u_x, u_{x'}\in \mathsf {child} (u)\) with \({{\,\mathrm{lca}\,}}_T(x,z')\preceq _T u_x\) and \({{\,\mathrm{lca}\,}}_T(x',z)\preceq _T u_{x'}\). By construction, we therefore have either \({{\,\mathrm{lca}\,}}_T(x,y)\prec _T{{\,\mathrm{lca}\,}}(x',y)\) or \({{\,\mathrm{lca}\,}}_T(x,y)={{\,\mathrm{lca}\,}}(x',y)\succeq _T u\). The first case implies \({{\,\mathrm{lca}\,}}_T(y,z')\prec _T u={{\,\mathrm{lca}\,}}_T(y,z)\), which contradicts \(yz\in E(G)\). Hence, it must hold \({{\,\mathrm{lca}\,}}_T(x,y)={{\,\mathrm{lca}\,}}(x',y)\succeq _T u\) and thus, \(x'\in N_r^+(y)\) because \(x\in N_r^+(y)\). Consequently, since \(x'y\notin E(G)\), there must be some \(y'\in L[s]\) such that \({{\,\mathrm{lca}\,}}_T(x',y')\prec _T {{\,\mathrm{lca}\,}}_T(x',y)\). The same argumentation as in Case (i) shows that \({{\,\mathrm{lca}\,}}_T(x',z) \prec _T u\) implies either \({{\,\mathrm{lca}\,}}_T(z,y')\prec _T u \preceq _T {{\,\mathrm{lca}\,}}_T(x',y)\) or \({{\,\mathrm{lca}\,}}_T(z,y')={{\,\mathrm{lca}\,}}_T(x',y')\prec _T {{\,\mathrm{lca}\,}}_T(x',y)\), which in either case contradicts \(yz\in E(G)\). We therefore conclude that Case (iii) is impossible. \(\square \)
We immediately find the following result that links good quartets to 3-RBMGs of Type (B):
Lemma 33
Let \((G,\sigma )\) be an undirected, connected, \({\mathsf {S} }\)-thin and properly 3-colored graph that contains an induced path P on four vertices. If \((G,\sigma )\) satisfies (B1) to (B4.b) w.r.t. P, then there exists a tree \((T,\sigma )\) explaining \((G,\sigma )\) such that P is a good quartet in \(\vec {G}(T,\sigma )\).
Proof
Suppose that \((G,\sigma )\) satisfies (B1) to (B4.b) w.r.t. P. Then, by Lemma 25, \((G,\sigma )\) is a 3-RBMG of Type (B). Thus, according to Lemma 24, there exists a Type (II\(^*\)) tree \((T,\sigma )\) with root \(\rho _T\) such that \(L_t^P=L(T(v_1))\), \(L_s^P=L(T(v_2))\) for distinct \(v_1,v_2\in \mathsf {child} _T(\rho _T){\setminus } L\) and \(L_*^P=\mathsf {child} _T(\rho _T)\cap L\), that explains \((G,\sigma )\). In particular, by Property (B1), we have \(P:=\langle x y z x'\rangle \) with \(\sigma (x)=\sigma (x')=r\), \(\sigma (y)=s\) and \(\sigma (z)=t\) for distinct colors r, s, t. Now, as \(x,y\in L_t^P\) and \(x',z\in L_s^P\) by Lemma 25 and, by definition, \(\sigma (L_t^P)=\{r,s\}\), \(\sigma (L_s^P)=\{r,t\}\), one easily checks that P is indeed a good quartet in \(\vec {G}(T,\sigma )\). \(\square \)
We continue with some basic result about ugly quartets before analyzing good and bad quartets in more details.
Lemma 34
Let \(\langle xyx'z\rangle \) be an ugly quartet in some connected \({\mathsf {S} }\)-thin 3-RBMG \((G,\sigma )\) and \((T,\sigma )\) with root \(\rho _T\) a tree of Type (II) or (III) that explains \((G,\sigma )\). Then the children \(v_a\in \mathsf {child} (\rho _T)\) with \(a\in \{x,x',y,z\}\) and \(a\preceq _T v_a\) satisfy exactly one of the following conditions:
- (i)
\(v_x=x\), \(v_{x'}=v_z\), \(v_y\ne y\), and \(v_x\), \(v_y\), \(v_z\) are pairwise distinct,
- (ii)
\(v_x=v_{x'}=v_z\ne v_y\) and \(v_y\ne y\),
- (iii)
\(v_x\ne x\), \(v_{x'}=x'\), \(v_y=v_z\), and \(v_x\), \(v_{x'}\), \(v_y\) are pairwise distinct,
- (iv)
\(v_x\ne x\), \(v_{x'}=x'\), \(v_y\ne y\), \(v_z=z\), and \(v_x\), \(v_{x'}\), \(v_y\), \(v_z\) are pairwise distinct,
- (v)
\(v_x\ne x\), \(v_{x'}=x'\), \(v_y=y\), \(v_z\ne z\), and \(v_x\), \(v_{x'}\), \(v_y\), \(v_z\) are pairwise distinct.
In particular, x, \(x'\), and y can never reside within the same subtree \(T(v_x)\). Indeed, all cases may appear.
Proof
Let L be the vertex set of G and r, s, t be three distinct colors in \((G,\sigma )\), where \(\sigma (x)=\sigma (x')=r\), \(\sigma (y)=s\), and \(\sigma (z)=t\).
We start by considering the two Cases (a) \(v_x=x\), i.e., \(x\in \mathsf {child} (\rho _T)\) and (b) \(v_x\ne x\).
We first assume Case (a), i.e., \(x\in \mathsf {child} (\rho _T)\). Note first that this immediately implies \(x'\notin \mathsf {child} (\rho _T)\), i.e., \(v_{x'}\ne x'\) because \((G,\sigma )\) is \({\mathsf {S} }\)-thin (cf. Lemma 18). Moreover, we have \(s\notin \sigma (L(T(v_{x'})))\) because \(x'y\in E(G)\) and thus, since \(v_{x'}\ne x'\), Lemma 8 implies that \(t\in \sigma (L(T(v_{x'})))\). Consequently, \(z\in L(T(v_{x'}))\) as otherwise, there is some \(z'\in L(T(v_{x'}))\) such that \({{\,\mathrm{lca}\,}}(x',z')\prec _T {{\,\mathrm{lca}\,}}(x',z)\), which contradicts \(x'z\in E(G)\). Since \(xy\in E(G)\), \(x\in \mathsf {child} (\rho _T)\) implies either \(y\in \mathsf {child} (\rho _T)\) or \(\sigma (L(T(v_y)))=\{s,t\}\) as otherwise \({{\,\mathrm{lca}\,}}(x'',y)\prec _T {{\,\mathrm{lca}\,}}(x,y)\) for some \(x''\in L(T(v_y))\cap L[r]\), contradicting \(xy\in E(G)\). If the first case is true, we have, by construction, \({{\,\mathrm{lca}\,}}(y,z)\preceq _T {{\,\mathrm{lca}\,}}(y,z')\) and \({{\,\mathrm{lca}\,}}(y,z)\preceq _T {{\,\mathrm{lca}\,}}(y',z)\) for any \(y'\in L[s]\) and \(z'\in L[t]\), i.e., \(yz\in E(G)\); a contradiction since \(\langle xyx'z\rangle \) is an induced \(P_4\). Hence, we have \(\sigma (L(T(v_y)))=\{s,t\}\), which in particular implies \(v_y\ne y\) and \(v_y\ne v_{x'}, v_x\). Using Lemma 19, one easily checks that, if \(\mathsf {par} (x')=\mathsf {par} (z)\), \(\langle xyx'z\rangle \) is indeed an induced \(P_4\) in \((G,\sigma )\), which finally shows Statement (i).
Now assume that Case (b) is true, i.e., \(v_x\ne x\). Then, by Lemma 8, the subtree \((T(v_x),\sigma _{|L(T(v_x))})\) must contain at least two colors. Assume first, for contradiction, that \(s\in \sigma (L(T(v_x)))\). Then, as \(xy,x'y\in E(G)\), Lemma 19 implies that \(x'\in L(T(v_x))\) and \(\mathsf {par} (x)=\mathsf {par} (x')=\mathsf {par} (y)\), which contradicts the \({\mathsf {S} }\)-thinness of \((G,\sigma )\). Hence, \(\sigma (L(T(v_x)))=\{r,t\}\), and in particular \(v_x\ne v_y\).
If \(v_x=v_{x'}\), it follows from \(x'z\in E(G)\) that \(z\preceq _T v_x\) (cf. Lemma 19), i.e., \(v_x=v_z\). Moreover, since \(s\notin \sigma (L(T(v_x)))\) and \(yz\notin E(G)\), Lemma 19(iv) implies \(v_y\ne y\). Hence, by Lemma 8, it must hold \(\sigma (L(T(v_y)))=\{s,t\}\). Choosing \(\mathsf {par} (x')=\mathsf {par} (z)\ne \mathsf {par} (x)\), one can again use Lemma 19 in order to show that \(\langle xyx'z\rangle \) forms an induced \(P_4\), which proves (ii).
On the other hand, if \(v_x\ne v_{x'}\), then \(xy,x'y\in E(G)\) requires \({{\,\mathrm{lca}\,}}(x,y)={{\,\mathrm{lca}\,}}(x',y)\), hence \(v_y\ne v_x,v_{x'}\). Again, \(x'y\in E(G)\) then implies \(s\notin \sigma (L(T(v_{x'})))\). Since \(\sigma (L(T(v_{x'})))= \sigma (L(T(v_x)))=\{r,t\}\) is not possible by construction of a tree of Type (II) or (III) contains only color r, hence \(v_{x'}=x'\) by Lemma 8. It finally remains to distinguish the two cases \(v_y=v_z\) and \(v_y\ne v_z\). In the first case, if \(\mathsf {par} (y)\ne \mathsf {par} (z)\) in \((T,\sigma )\), we can apply Lemma 19 to show \(yz\notin E(G)\) and furthermore, that \(\langle xyx'z\rangle \) is again an induced \(P_4\). This yields Statement (iii).
If the latter case is true, i.e., \(v_y\ne v_z\), then, as \(xy,x'y,x'z\in E(G)\), we have in particular \(r\notin \sigma (L(T(v_y))),\sigma (L(T(v_z)))\). Furthermore, since \(yz\notin E(G)\), there is either some \(z'\in L(T(v_y))\cap L[t] \) such that \({{\,\mathrm{lca}\,}}(y,z')\prec _T{{\,\mathrm{lca}\,}}(y,z)\), or some \(y'\in L(T(v_z))\cap L[s] \) such that \({{\,\mathrm{lca}\,}}(y',z)\prec _T{{\,\mathrm{lca}\,}}(y,z)\). Note that, since \(v_y\ne v_z\), \(\sigma (L(T(v_y)))=\sigma (L(T(v_z)))=\{s,t\}\) is not possible by construction of \((T,\sigma )\). Hence, by applying Lemma 8 to these two cases, we either obtain (iv) or (v). Again, Lemma 19 easily shows that \(\langle xyx'z\rangle \) is an induced \(P_4\) in \((G,\sigma )\), which concludes the proof. \(\square \)
We will from now on focus on good and bad quartets only as they are of particular interest for the characterization of Type (B) 3-RBMGs. We start with some basic result.
Lemma 35
Let \((G,\sigma )\) be an RBMG and \(P:=\langle xyzx'\rangle \) an induced \(P_4\) in \((G,\sigma )\) with \(\sigma (x)=\sigma (x')\), let \((T,\sigma )\) be a tree explaining \((G,\sigma )\) and let \(v:={{\,\mathrm{lca}\,}}_T(x,x',y,z)\). Then the distinct children \(v_i \in \mathsf {child} (v)\) satisfy exactly one of the three alternatives
- (i)
\(x,y\preceq _T v_1\) and \(x',z\preceq _T v_2\),
- (ii)
\(x\preceq _T v_1\), \(y,z\preceq _T v_2\), and \(x' \preceq _T v_3\),
- (iii)
\(x\preceq _T v_1\), \(y\preceq _T v_2\), \(x'\preceq _T v_3\), and \(z\preceq _T v_4\).
Indeed, all three cases may appear.
Proof
Let \(\sigma (x)=\sigma (x')=r\), \(\sigma (y)=s\), and \(\sigma (z)=t\).
Suppose first \(x,y \in L(T(v_1))\) for some \(v_1\in \mathsf {child} (v)\). If \(z\preceq _T v_1\), then \(x'\in L(T(v_1))\) since otherwise \({{\,\mathrm{lca}\,}}_T(x,z)\prec _T{{\,\mathrm{lca}\,}}_T(x',z)\), contradicting \(zx'\in E(G)\). Thus, \({{\,\mathrm{lca}\,}}_T(x,x',y,z)\prec _T v\); a contradiction to the definition of v. Hence, \(z\notin L(T(v_1))\). Then, \(yz\in E(G)\) implies that \(t\notin \sigma (L(T(v_1)))\), hence in particular \(v={{\,\mathrm{lca}\,}}_T(x,z)\preceq _T {{\,\mathrm{lca}\,}}_T(x,z')\) for any \(z'\in L[t]\), i.e., \(z\in N^+_t(x)\). Since \(xz\notin E(G)\), it must therefore hold \({{\,\mathrm{lca}\,}}_T(x',z)\prec _T {{\,\mathrm{lca}\,}}_T(x,z)=v\), thus \(x',z\in L(T(v_2))\) for some \(v_2\in \mathsf {child} (v){\setminus } \{v_1\}\). This implies Case (i).
Now suppose x and y are located in different subtrees below v, i.e., \(x\preceq _T v_1\) and \(y\preceq _T v_2\) for distinct children \(v_1,v_2\in \mathsf {child} (v)\). Since \(xy\in E(G)\) and \({{\,\mathrm{lca}\,}}_T(x,y)=v\), we conclude that \(r\notin \sigma (L(T(v_2)))\) and \(s \notin \sigma (L(T(v_1)))\). This immediately implies \(x'\notin L(T(v_1))\) as otherwise (a) \({{\,\mathrm{lca}\,}}_T(x,y)={{\,\mathrm{lca}\,}}_T(x',y)\) results in \(x'\in N^+_r(y)\), and (b) \({{\,\mathrm{lca}\,}}_T(x',y)\preceq _T {{\,\mathrm{lca}\,}}_T(x',y')\) for any \(y'\in L[s]\), hence \(x'y\in E(G)\); a contradiction. Therefore, there must be a child \(v_3\ne v_1,v_2\) of v such that \(x'\preceq _T v_3\). As a consequence, z cannot be contained in \(L(T(v_1))\) since this would imply \({{\,\mathrm{lca}\,}}_T(x,z)\prec _T {{\,\mathrm{lca}\,}}_T(x',z)\), contradicting \(x'z\in E(G)\). Suppose \(z\in L(T(v_3))\). Then, since \(yz\in E(G)\), we have \(t\notin \sigma (L(T(v_2)))\) and \(s\notin \sigma (L(T(v_3)))\). As we already know \(r\notin \sigma (L(T(v_2)))\), we conclude \(\sigma (L(T(v_2)))=\{s\}\) and \(\sigma (L(T(v_3)))=\{r,t\}\). Clearly, this implies \(yx'\in E(G)\); a contradiction. Therefore, \(z\notin L(T(v_3))\), thus we either have \(z\preceq _T v_2\) or there exists another child \(v_4\) of v (\(v_4\ne v_1,v_2,v_3\)) such that \(z\preceq _T v_4\). The latter shows that one of the Cases (ii) and (iii) may occur. However, we need to ensure that both can happen given the existence of the induced \(P_4\)\(\langle xyzx'\rangle \). Let us first assume \(z\in L(T(v_2))\), thus \(\sigma (L(T(v_2)))=\{s,t\}\). If \(\sigma (L(T(v_1)))=\{r,t\}\) and \(\sigma (L(T(v_3)))=\{r,s\}\), then one easily checks that \(\langle xyzx'\rangle \) is an induced \(P_4\) in \((G,\sigma )\), which implies statement (ii). On the other hand, if \(z\preceq _T v_4\) and \(\sigma (L(T(v_1)))=\{r,t\}\), \(\sigma (L(T(v_2)))=\{s\}\), \(\sigma (L(T(v_3)))=\{r,s\}\)\(\sigma (L(T(v_4)))=\{t\}\), then \(\langle xyzx'\rangle \) also forms an induced \(P_4\) in \((G,\sigma )\), i.e., Case (iii) is true. \(\square \)
It turns out that the location of good quartets in any tree is strictly constrained:
Lemma 36
Let \((\vec {G},\sigma )\) be a BMG containing a good quartet \(\langle xyzx' \rangle \), \((T,\sigma )\) a tree explaining \((\vec {G},\sigma )\) and \(v:={{\,\mathrm{lca}\,}}(x,x',y,z)\). Then, \(x,y \preceq _T v_1\) and \(x',z\preceq _T v_2\) for some distinct \(v_1, v_2\in \mathsf {child} (v)\).
Proof
Let \(v:={{\,\mathrm{lca}\,}}_T(x,x',y,z)\) and \(v_1\in \mathsf {child} (v)\) such that \(x\preceq _T v_1\). Suppose first \(y\notin L(T(v_1))\), hence in particular \({{\,\mathrm{lca}\,}}_T(y,x')\preceq _T v = {{\,\mathrm{lca}\,}}_T(y,x)\). Since \(xy\in E(G(T,\sigma ))\), this implies \(x'\in N^+_{\sigma (x)}(y)\) in \((\vec {G},\sigma )\); a contradiction to \(\langle xyzx' \rangle \) forming a good quartet. Hence, \(y\preceq _T v_1\). As \((T,\sigma )\) must satisfy one of the three cases of Lemma 35 and the only possible case is (i), we can now conclude \(x,y\preceq _T v_1\) and \(x',z\preceq _T v_2\). \(\square \)
Note that the latter result in addition shows that the Cases (ii) and (iii) in Lemma 35 must correspond to bad quartets. Lemma 36 now can be used to show that the any good quartet in an BMG is endowed with the same coloring.
Corollary 8
Let \((G,\sigma )\) be a connected \({\mathsf {S} }\)-thin 3-RBMG of Type (B), \((\vec {G},\sigma )\) a BMG containing \((G,\sigma )\) as symmetric part, and let \(Q=\langle xyzx'\rangle \) with \(\sigma (x)=\sigma (x')\) be a good quartet in \((\vec {G},\sigma )\). Then every good quartet with \(\langle x_1y_1z_1x_1'\rangle \in {\mathcal {P}}_4\) has colors \(\sigma (x_1)=\sigma (x_1')=\sigma (x)\), \(\sigma (y_1)=\sigma (y)\), and \(\sigma (z_1)=\sigma (z)\).
Proof
Since \((G,\sigma )\) a of Type (B), any leaf-colored tree \((T,\sigma )\) with root \(\rho _T\) explaining \((G,\sigma )\) is of Type (II) (cf. Theorem 4). Hence, there are distinct \(v_1, v_2\in \mathsf {child} (\rho _T)\) with \(|\sigma (L(T(v_1)))|=|\sigma (L(T(v_2)))|=2\) and \(\mathsf {child} (\rho _T){\setminus } \{v_1,v_2\}\subset L\). By Lemma 36, we have \(x,y\preceq _T v_1\) and \(x',z\preceq _T v_2\), hence \(\sigma (L(T(v_1)))=\{\sigma (x),\sigma (y)\}\) and \(\sigma (L(T(v_2)))=\{\sigma (x),\sigma (z)\}\). Therefore, the statement follows directly from Lemma 36. \(\square \)
We are now in the position to formulate one of the main results of this section:
Lemma 37
Let \((G,\sigma )\) be a connected \({\mathsf {S} }\)-thin 3-RBMG of Type (B) and \((\vec {G},\sigma )\) a BMG containing \((G,\sigma )\) as its symmetric part. Moreover, let \(L_s^Q\), \(L_t^Q\), and \(L_*^Q\) be defined w.r.t. a good quartet \(Q:=\langle x_1y_1z_1x_1'\rangle \) where \(x_1,x_1'\in L[r]\), \(y_1\in L[s]\), and \(z_1\in L[t]\) for distinct colors r, s, t. Then, for any good quartet \(Q'\), it holds \(L_s^{Q'}=L_s^Q\), \(L_t^{Q'}=L_t^Q\), and \(L_*^{Q'}=L_*^Q\).
Proof
Let \((T,\sigma )\) with root \(\rho _T\) be a leaf-colored tree that explains \((\vec {G},\sigma )\) and thus, also \((G,\sigma )\). Since \((G,\sigma )\) is of Type (B), we can choose \((T,\sigma )\) to be of Type (II) by Theorem 4, i.e., there are distinct children \(v_1,v_2\in \mathsf {child} (\rho _T)\) with \(|\sigma (L(T(v_1)))|=|\sigma (L(T(v_2)))|=2\) such that these two subtrees have exactly one color in common, and \(\mathsf {child} (\rho _T){\setminus } \{v_1,v_2\}\subset L\). Applying Lemma 24, we can choose \((T,\sigma )\) such that it is of Type (II\(^*\)) and satisfies \(L_t^Q=L(T(v_1))\), \(L_s^Q=L(T(v_2))\) and \(L_*^Q=\mathsf {child} (\rho _T)\cap L\). On the other hand, Lemma 36 implies \(x_1,y_1 \preceq _T v_1\) and \(x_1',z_1\preceq _T v_2\).
Now let \(Q':=\langle x_2y_2z_2x_2'\rangle \ne Q\) be another good quartet in \((\vec {G},\sigma )\). By Corollary 8, we have \(x_2,x_2'\in L[r]\), \(y_2\in L[s]\) and \(z_2\in L[t]\). Lemma 36 and the structure of Type (II) trees then imply \(x_2,y_2\preceq _T v_1\) and \(x_2',z_2\preceq _T v_2\). Consider first \(L_t^{Q'}\) and let \(x\in L[r],y\in L[s]\). Then, by definition, \(y\in L_t^{Q'}\) if and only if \(\langle x'yz_2 \rangle \in {\mathcal {P}}_3\) for each \(x'\in N_r(y)\). Since any two leaves of color s and t are reciprocal best matches in \((G,\sigma )\) by Lemma 19(iii) and \(x'z_2 \notin E(G)\) for any \(x'\in N_r(y)\) only if \(x'\notin L(T(v_2))\) by cf. Lemma 19(i)+(iv), we have \(\langle x'yz_2 \rangle \in {\mathcal {P}}_3\) for any \(x'\in N_r(y)\) if and only if \(\langle x'yz_1 \rangle \in {\mathcal {P}}_3\) for any \(x'\in N_r(y)\). Hence, \(y\in L_t^{Q'}\) if and only if \(y\in L_t^Q\), i.e., \(L_t^Q\cap L[s]=L_t^{Q'}\cap L[s]\). If \(N_s(x)=\emptyset \), the latter by definition of \(L_t^Q\) immediately implies that \(x\in L_t^{Q'}\) if and only if \(x\in L_t^Q\). On the other hand, if \(N_s(x)\ne \emptyset \), then \(x\in L_t^{Q'}\) if and only if \(N_r(y')=\{x\}\) for some induced \(P_3\)\(\langle xy'z_2 \rangle \). This can only be true if \(y'\in L(T(v_1))\) since otherwise, \(y'z_2 x_2'\) forms a circle, thus \(|N_r(y')|>1\). Consequently, \(x\in L(T(v_1))\) by Lemma 19(i). Since \(y'z'\in E(G)\) for any \(y'\in L[s], z'\in L[t]\) by Lemma 19(ii) and \(x'z\notin E(G)\) for any \(z\in L(T(v_2))\cap L[t]\) by Lemma 19(ii), we conclude that \(\langle xy'z_2\rangle \) is an induced \(P_3\) with \(N_r(y')=\{x\}\) if and only if \(\langle xy'z_1\rangle \) is an induced \(P_3\) with \(N_r(y')=\{x\}\), hence \(L_t^Q\cap L[r]=L_t^{Q'}\cap L[r]\). We therefore conclude \(L_t^Q=L_t^{Q'}\).
By symmetry, an analogous argument shows \(L_s^Q=L_s^{Q'}\). Together, this finally implies \(L_*^Q=L_*^{Q'}\), completing the proof. \(\square \)
Figure 13 shows that good and bad quartets do not necessarily imply the same leaf sets \(L_s^P\), \(L_t^P\).
We simplify the notation using the following abbreviations:
Definition 18
\((G_{rst},\sigma _{rst}):=(G[L[r]\cup L[s]\cup L[t]], \sigma _{|L[r]\cup L[s]\cup L[t]})\) and \((T_{rst},\sigma _{rst}):=(T_{|L[r]\cup L[s]\cup L[t]}, \sigma _{|L[r]\cup L[s]\cup L[t]})\) for any three colors \(r,s,t\in S\).
The restriction of a BMG \(\vec {G}(T,\sigma )\) to a subset \(S'\subset S\) of colors is an induced subgraph of \(\vec {G}(T,\sigma )\) explained by the restriction of \((T,\sigma )\) to the leaves with colors in \(S'\), and thus again a BMG (Geiß et al. 2019a, Observation 1). Since \(G(T,\sigma )\) is the symmetric part of \(\vec {G}(T,\sigma )\), it inherits this property. In particular, we have
Observation 6
If \((G,\sigma )\) is an n-RBMG, \(n\ge 3\) explained by \((T,\sigma )\), then for any three colors \(r,s,t \in S\), the restricted tree \((T_{rst},\sigma _{rst})\) explains \((G_{rst},\sigma _{rst})\), and \((G_{rst},\sigma _{rst})\) is an induced subgraph of \((G,\sigma )\).
This observation will play an important role in the proof of the following lemma as well as in Sect. F.
Lemma 38
Let \((\vec {G},\sigma )\) be a BMG. Then, the symmetric part \((G,\sigma )\) contains an induced 3-colored \(P_4\) whose endpoints have the same color if and only if \((\vec {G},\sigma )\) contains a good quartet.
Proof
Note that, if \((\vec {G},\sigma )\) contains a good quartet, then its symmetric part \((G,\sigma )\) by definition contains a 3-colored \(P_4\)\(\langle abcd \rangle \) with \(\sigma (a)=\sigma (d)\).
Conversely, suppose that \((G,\sigma )\) contains a 3-colored induced \(P_4\)\(\langle abcd \rangle \) whose endpoints have the same color \(\sigma (a)=\sigma (d)\). Moreover, let S be the color set of \((G,\sigma )\) and \((T,\sigma )\) be a tree explaining \((\vec {G},\sigma )\) and thus also \((G,\sigma )\). W.l.o.g. we can assume that the three colors of \(\langle abcd \rangle \) are \(r,s,t\in S\) without explicitly stating the particular coloring of the vertices a, b, c, and d. By definition, \((G_{rst},\sigma _{rst})\) contains the induced path \(\langle abcd \rangle \). W.l.o.g. we may assume that \((G_{rst},\sigma _{rst})\) is connected; otherwise the proof works analogously for the connected component of \((G_{rst},\sigma _{rst})\) that contains \(\langle abcd \rangle \).
Let us first assume that \((G_{rst},\sigma _{rst})\) is \({\mathsf {S} }\)-thin. In this case, we can apply Theorem 4 and conclude that \((G_{rst},\sigma _{rst})\) is either of Type (B) or (C), i.e., the restricted tree \((T_{rst},\sigma _{rst})\) with root \(\rho :={{\,\mathrm{lca}\,}}_T(L[r]\cup L[s] \cup L[t])\) that explains \((G_{rst},\sigma _{rst})\) must be of Type (II) or (III). Hence, there are distinct children \(v_1,v_2\in \mathsf {child} (\rho )\) with \(\sigma (L(T_{rst}(v_1)))=\{r,s\}\) and \(\sigma (L(T_{rst}(v_2)))=\{r,t\}\) for distinct colors r, s, t (up to permutation of the colors). Then there exist leaves \(x,y\in L(T_{rst}(v_1))\) and \(x',z\in L(T_{rst}(v_2))\) with \(x,x'\in L[r]\), \(y\in L[s]\), and \(z\in L[t]\) such that \(xy,x'z\in E(G_{rst})\) (cf. Lemma 10). Moreover, Lemma 19(ii) implies that \(yz\in E(G_{rst})\) as well as \(xz,x'y\notin E(G_{rst})\). Hence, \(\langle xyzx'\rangle \) is an induced \(P_4\) in \((G_{rst},\sigma _{rst})\) and thus, by Observation 6, also in \((G,\sigma )\). Since \(t\notin \sigma (L(T(v_1)))\), we have \(\rho ={{\,\mathrm{lca}\,}}_T(x,z)\preceq _T {{\,\mathrm{lca}\,}}_T(x,z')\) for any \(z'\in L[t]\), i.e., \(z\in N_t^+(x)\) in \((T,\sigma )\). In particular, \(xz\notin E(G)\) then immediately implies \(x\notin N_r^+(z)\). One similarly argues that \(y\in N_s^+(x')\) and \(x'\notin N_r^+(y)\) in \((T,\sigma )\), hence \((x,z), (x',y)\in E(\vec {G})\) and \((z,x),(y,x')\notin E(\vec {G})\). Therefore, \(\langle xyzx'\rangle \) is a good quartet in \((\vec {G},\sigma )\).
Now, suppose that \((G_{rst},\sigma _{rst})\) is not \({\mathsf {S} }\)-thin. In this case, we apply the same arguments as above to the quotient graph \((G_{rst}/{\mathsf {S} },\sigma _{rst}/{\mathsf {S} })\) and conclude that there exists a good quartet \(\langle [a][b][c][d] \rangle \) induced by the tree \((T_{rst},\sigma _{rst})\) that explains \((G_{rst}/{\mathsf {S} },\sigma _{rst}/{\mathsf {S} })\). Let \(x\in [a], y\in [b], z\in [c]\) and \(x'\in [d]\). Lemma 5 implies that \(\langle xyzx'\rangle \) is an induced \(P_4\) with \(\sigma (x) = \sigma (x')\) in \((G_{rst},\sigma _{rst})\) and thus, by Observation 6, also in \((G,\sigma )\). To conclude that \(\langle xyzx'\rangle \) is a good quartet it remains to show that \((x,z), (x',y)\in E(\vec {G})\) and \((z,x),(y,x')\notin E(\vec {G})\). In order to see this, observe first that \(([a],[c]), ([d],[b])\in E(\vec {G}(T_{rst},\sigma _{rst}))\) and \(([c],[a]), ([b],[d])\notin E(\vec {G}(T_{rst},\sigma _{rst}))\) since \(\langle [a][b][c][d] \rangle \) is a good quartet induced by \((T_{rst},\sigma _{rst})\). To obtain a tree \(({\hat{T}}, {\hat{\sigma }})\) that explains \((G_{rst}, \sigma _{rst})\), we can proceed as in the proof of the “if-direction” in Lemma 7 and simply replace all edges \(\mathsf {par} ([v])[v]\) in \(T_{rst}\) by edges \(\mathsf {par} ([v])v'\) for all \(v'\in [v]\) and putting \({\hat{\sigma }}(v') = \sigma _{rst}([v])\). Clearly, the latter construction and \(([a],[c]), ([d],[b])\in E(\vec {G}(T_{rst},\sigma _{rst}))\) and \(([c],[a]), ([b],[d])\notin E(\vec {G}(T_{rst},\sigma _{rst}))\) implies that \((x,z), (x',y)\in E(\vec {G}({\hat{T}}, {\hat{\sigma }}))\) and \((z,x),(y,x')\notin E(\vec {G}({\hat{T}}, {\hat{\sigma }}))\). Therefore, \(\langle xyzx'\rangle \) is a good quartet induced by \(({\hat{T}}, {\hat{\sigma }})\) and thus, in \((G_{rst},\sigma _{rst})\). Now, by Observation 6 implies that \(\langle xyzx'\rangle \) is a good quartet in \((\vec {G},\sigma )\). \(\square \)
Since every bad quartet induces in particular an induced \(P_4\) with endpoints of the same color, Lemma 38 immediately implies:
Corollary 9
If a BMG \((\vec {G},\sigma )\) contains a bad quartet, then it contains a good quartet. In particular, any BMG \((\vec {G},\sigma )\) whose symmetric part contains a 3-RBMG of Type (B) or (C) as induced subgraph, contains a good quartet.
Proof
The first statement is an immediate consequence of Lemma 38. If \((G,\sigma )\) is a 3-RBMG of Type (B), then, by definition, it contains an induced \(P_4\) of the form (r, s, t, r) for distinct colors r, s, t. Hence, by Lemma 32, this \(P_4\) is either a good or a bad quartet in \((\vec {G},\sigma )\), where \((\vec {G},\sigma )\) is a BMG whose symmetric part contains \((G,\sigma )\) as induced subgraph. Lemma 38 thus implies that \((\vec {G},\sigma )\) contains a good quartet. If \((G,\sigma )\) is a 3-RBMG of Type (C), it must, by definition, contain an induced \(C_6\) of the form (r, s, t, r, s, t). In particular, it contains an induced \(P_4\) whose endpoints are of the same color, thus we can again apply the same argumentation to complete the proof. \(\square \)
The converse of Corollary 9 is, however, not true. As an example, consider the tree \(T=((x,y),(x'z))\) in Newick format with \(\sigma (x)=\sigma (x')=r\), \(\sigma (y)=s\), \(\sigma (z)=t\). The graph \(G(T,\sigma )\) is the \(P_4\)\(\langle xyzx'\rangle \), which is of course uniquely defined. The BMG \(\vec {G}(T,\sigma )\) contains the directed edges \((x,z), (x',y)\) but not \((z,x), (y,x')\), hence \(Q=\{x,y,z,x'\}=V(T)\) is a good quartet.
We close this section with a variation of Lemma 36 for Type (C) RBMGs:
Lemma 39
Let \((G,\sigma )\) be a connected \({\mathsf {S} }\)-thin 3-RBMG of Type (C) that contains an induced hexagon \(H:=\langle x_1 y_1 z_1 x_2 y_2 z_2 \rangle \) with \(|N_t(x_1)|>1\), where \(x_i\in L[r], y_i\in L[s], z_i\in L[t]\) for distinct colors r, s, t. Moreover, let \((T,\sigma )\) explain \((G,\sigma )\) and \(v:={{\,\mathrm{lca}\,}}_T(x_1,x_2,y_1,y_2,z_1,z_2)\). Then,
- (i)
\(\langle x_1y_1z_1x_2\rangle \), \(\langle z_1x_2y_2 z_2\rangle \), and \(\langle y_2z_2x_1y_1\rangle \) are good quartets in \(\vec {G}(T,\sigma )\),
- (ii)
\(\langle y_1z_1x_2y_2\rangle \), \(\langle x_2y_2 z_2x_1\rangle \), and \(\langle z_2x_1y_1z_1\rangle \) are bad quartets in \(\vec {G}(T,\sigma )\), and
- (iii)
\(x_1,y_1\preceq _T v_1\), \(x_2,z_1 \preceq _T v_2\), and \(y_2,z_2\preceq _T v_3\) for some distinct \(v_1,v_2,v_3\in \mathsf {child} _T(v)\).
Proof
We start with proving Properties (i) and (ii). By definition and Lemma 32, \(\langle x_1y_1z_1x_2\rangle \) is either a good or a bad quartet in \(\vec {G}(T,\sigma )\). Assume, for contradiction, that it is a bad quartet in \(\vec {G}(T,\sigma )\), thus, in particular, \((z_1,x_1)\in E(\vec {G}(T,\sigma ))\) and \((x_1,z_1)\notin E(\vec {G}(T,\sigma ))\). Hence, as also \(\langle z_2x_1y_1z_1\rangle \) must be either a good or a bad quartet in \(\vec {G}(T,\sigma )\), this immediately implies that \(\langle z_2x_1y_1z_1\rangle \) is a good quartet in \(\vec {G}(T,\sigma )\). Let \(w:={{\,\mathrm{lca}\,}}_T(z_2,x_1,y_1,z_1)\). Lemma 36 then implies that there exist distinct \(w_1,w_2\in \mathsf {child} _T(w)\) such that \(z_2, x_1 \preceq _T w_1\) and \(y_1,z_1\preceq _T w_2\). Clearly, as \(x_1y_1\in E(G)\) and \({{\,\mathrm{lca}\,}}_T(x_1,y_1)=w\), we must have \(s\notin \sigma (L(T(w_1)))\). Since \(|N_t(x_1)|>1\), there is a leaf \(z\in L[t]{\setminus } \{z_1,z_2\}\) such that \(x_1z\in E(G)\). By Lemma 10, there exists an edge \(x'z'\in E(G(T,\sigma ))\) with \(x'\in L[r]\cap L(T(w'))\), \(z'\in L[t]\cap L(T(w'))\) for any inner vertex \(w'\preceq _T w\). One easily verifies that this and \(x_1z_2\in E(G)\) necessarily implies that the leaves \(x_1\), \(z_2\), and z must all be incident to the same parent in T. However, we then have \(N(z)=N(z_2)\), i.e., z and \(z_2\) belong to the same \({\mathsf {S} }\)-class; a contradiction since \((G,\sigma )\) is \({\mathsf {S} }\)-thin. We therefore conclude that \(\langle x_1y_1z_1x_2\rangle \) must be a good quartet. Hence, \((x_2,y_1), (x_1,z_1)\in E(\vec {G}(T,\sigma ))\) and \((y_1,x_2), (z_1,x_1)\notin E(\vec {G}(T,\sigma ))\), which, as a consequence of Lemma 32, immediately implies that \(\langle y_1z_1x_2y_2\rangle \) and \(\langle z_2x_1y_1z_1\rangle \) are bad quartets in \(\vec {G}(T,\sigma )\). This similarly implies that \(\langle z_1x_2y_2 z_2\rangle \) and \(\langle y_2z_2x_1y_1\rangle \) are good quartets, from which we finally conclude that \(\langle x_2y_2 z_2x_1\rangle \) is a bad quartet in \(\vec {G}(T,\sigma )\).
We continue with showing Property (iii). Property (i) implies that \(\langle x_1y_1z_1x_2\rangle \) and \(\langle z_1x_2y_2 z_2\rangle \) are good quartets in \(\vec {G}(T,\sigma )\). Hence, by Lemma 36, we have \(x_1,y_1\preceq _T w_1\), \(x_2,z_1 \preceq _T w_2\) for distinct \(w_1,w_2\in \mathsf {child} _T(u_1)\), where \(u_1:={{\,\mathrm{lca}\,}}_T(x_1,y_1,z_1,x_2)\), and \(y_2,z_2\preceq _T w'_1\), \(x_2,z_1 \preceq _T w'_2\) for distinct \(w'_1,w'_2\in \mathsf {child} _T(u_2)\), where \(u_2:={{\,\mathrm{lca}\,}}_T(y_2,z_2,z_1,x_2)\), respectively. Since \(u_1\) and \(u_2\) are both located on the path from \(z_1\) to the root of T, they must be comparable. Next, we show that \(u_1 = u_2\). Assume first, for contradiction, \(u_1\prec _T u_2\). Then, by construction, we have \({{\,\mathrm{lca}\,}}_T(x_2,y_1) = u_1\prec _T u_2={{\,\mathrm{lca}\,}}_T(x_2,y_2)\); a contradiction to \(x_2y_2\in E(G)\). Similarly, \(u_2\prec _T u_1\) yields a contradiction and thus, \(u_1=u_2=v\) and, in particular, \(w_2=w'_2\). It remains to show \(w_1\ne w'_1\). Assume, for contradiction, \(w_1= w'_1\). Then \({{\,\mathrm{lca}\,}}_T(x_1,y_2) \preceq _T w_1\prec _T v={{\,\mathrm{lca}\,}}_T(x_2,y_2)\); a contradiction to \(x_2y_2\in E(G)\). Hence, \(w_1\), \(w_2\), and \(w'_1\) are distinct children of v in T, which completes the proof. \(\square \)
Characterization of n-RBMGs
1.1 The general case: combination of 3-RBMGs
The key idea of characterizing n-RBMGs is to combine the information contained in their 3-colored induced subgraphs \((G_{rst},\sigma _{rst})\), cf. Definition 18. Observation 6 shows that \((G_{rst},\sigma _{rst})\) is a 3-colored induced subgraph of an n-RBMG explained by \((T_{rst},\sigma _{rst})\), and thus a 3-RBMG. Unfortunately, the converse of Observation 6 is in general not true. Figure 8 shows a 4-colored graph that is not a 4-RBMG while each of the four subgraphs induced by a triplet of colors is a 3-RBMG. We can, however, rephrase Observation 6 in the following way:
Observation 7
Let \((G,\sigma )\) be an n-RBMG for some \(n\ge 3\). Then, \((T,\sigma )\) explains \((G,\sigma )\) if and only if \((T_{rst},\sigma _{rst})\) explains \((G_{rst},\sigma _{rst})\) for all triplets of colors \(r,s,t \in S\).
Lemma 40
Let \((T_e,\sigma )\) be the tree obtained by contracting an inner edge of \((T,\sigma )\). Then \(G(T,\sigma )\) is a subgraph of \(G(T_e,\sigma )\).
Proof
Consider the edge \(e=xy\) in T. By construction \((T_e,\sigma )\le (T,\sigma )\), thus Eq. (3) implies \(N^+_{T}(u) \subseteq N^+_{T_e}(u)\) for all \(u\in L{\setminus } L(T(y))\) and \(N^+_{T}(v) = N^+_{T_e}(v)\) for all \(v\in L(T(y))\). It immediately follows \(N^-_{T}(w) \subseteq N^-_{T_e}(w)\) for all \(w\in L\). Hence, \(E(G)\subseteq E(G(T_e))\). Since the leaf set remains unchanged, \(L(T)=L(T_e)\), we conclude that the \(G(T,\sigma )\) is a subgraph of \(G(T_e,\sigma )\). \(\square \)
Definition 19
Let \((G,\sigma )\) be an n-RBMG. Then the tree set of\((G,\sigma )\) is the set \({\mathscr {T}}(G,\sigma ):=\{(T,\sigma ) \mid (T,\sigma ) \text { is least resolved and } G(T,\sigma )=(G,\sigma )\}\) of all leaf-colored trees explaining \((G,\sigma )\). Furthermore, we write \({\mathscr {T}}_{rst}(G,\sigma )\) for the set of all least resolved trees explaining the induced subgraphs \((G_{rst},\sigma _{rst})\).
The counterexample in Fig. 8 shows that the existence of a supertree for the tree set \({\mathscr {P}}:=\{T\in {\mathscr {T}}_{rst}(G_{rst},\sigma _{rst}),\,r,s,t\in S\}\) is not sufficient for \((G,\sigma )\) to be an n-RBMG. We can only obtain a substantially weaker result.
Theorem 7
A (not necessarily connected) undirected colored graph \((G,\sigma )\) is an n-RBMG if and only if (i) all induced subgraphs \((G_{rst},\sigma _{rst})\) on three colors are 3-RBMGs and (ii) there exists a supertree \((T,\sigma )\) of the tree set \({\mathscr {P}}:=\{T\in {\mathscr {T}}_{rst}(G,\sigma ) \mid r,s,t\in S\}\), such that \(G(T,\sigma )=(G,\sigma )\).
Proof
Suppose \((G,\sigma )\) is an n-RBMG explained by some tree \((T,\sigma )\). Then Observation 7 implies that \((G_{rst},\sigma _{rst})\) is a 3-RBMG that is explained by \((T_{rst},\sigma _{rst})\) for all triplets of colors \(r,s,t \in S\). By definition, each \((T_{rst},\sigma _{rst})\) is displayed by \((T,\sigma )\) and thus, \((T,\sigma )\) is a supertree of these trees. Hence, the conditions are necessary. Conversely, the existence of some supertree \((T,\sigma )\) with \(G(T,\sigma )=(G,\sigma )\), i.e., \((T,\sigma )\) explains \((G,\sigma )\), clearly implies that \((G,\sigma )\) is an n-RBMG. \(\square \)
1.2 Characterization of n-RBMGs that are cographs
Observation 8
Any undirected colored graph \((G,\sigma )\) is a cograph if and only if the corresponding \({\mathsf {S} }\)-thin graph \((G/{\mathsf {S} },\sigma _{/{\mathsf {S} }})\) is a cograph.
Proof
It directly follows from Lemma 5 that \((G,\sigma )\) contains an induced \(P_4\) if and only if \((G/{\mathsf {S} },\sigma _{/{\mathsf {S} }})\) contains an induced \(P_4\), which yields the statement. \(\square \)
We note in passing that point-determining (thin) cographs recently have attracted some attention in the literature (Li 2012).
Theorem 8
Let \((G,\sigma )\) be an n-RBMG with \(n\ge 3\), and denote by \((G'_{rst},\sigma '_{rst}):=(G_{rst}/S,\sigma _{rst}/S)\) the \({\mathsf {S} }\)-thin version of the 3-RBMG that is obtained by restricting \((G,\sigma )\) to the colors r, s, and t. Then \((G,\sigma )\) is a cograph if and only if every 3-colored connected component of \((G'_{rst},\sigma '_{rst})\) is a 3-RBMG of Type (A) for all triples of distinct colors r, s, t.
Proof
We first emphasize that distinct \({\mathsf {S} }\)-classes of some \({\mathsf {S} }\)-thin n-RBMG \((G,\sigma )\) may belong to the same \({\mathsf {S} }\)-class in \((G'_{rst},\sigma '_{rst}):=(G_{rst}/S,\sigma _{rst}/S)\). Likewise, distinct \({\mathsf {S} }\)-classes in \((G'_{rst},\sigma '_{rst})\) may belong to the same \({\mathsf {S} }\)-classes in \((G'_{r's't'},\sigma '_{r's't'})\). In the following, the vertex set of a connected component \((G_{rst}^*,\sigma _{rst}^*)\) of \((G'_{rst},\sigma '_{rst})\) will be denoted by \(L^*_{rst}\).
Recall that \((G,\sigma )\) is a cograph if and only if all of its connected components are cographs. Clearly, if \((G,\sigma )\) is an RBMG, then \((G_{rst},\sigma _{rst})\) and thus in particular \((G'_{rst},\sigma '_{rst})\) is a 3-RBMG (cf. Observation 6) for any three distinct colors r, s, t. Moreover, since \((G,\sigma )\) is a cograph, it cannot contain an induced \(P_4\), thus its induced subgraph on \(L[r]\cup L[s] \cup L[t]\) and therefore also \((G'_{rst},\sigma '_{rst})\) do not contain an induced \(P_4\) either, i.e., each connected component of \((G'_{rst},\sigma '_{rst})\) is again a cograph. Hence, by Observation 3, each of the connected components with three colors must be of Type (A).
Conversely, suppose that, for any distinct colors r, s, t, each connected component \((G_{rst}^*,\sigma _{rst}^*)\) of \((G'_{rst},\sigma '_{rst})\) is a 3-RBMG of Type (A). Thus, \((G_{rst}^*,\sigma _{rst}^*)\) is again \({\mathsf {S} }\)-thin. Observation 3 implies that \((G_{rst}^*,\sigma _{rst}^*)\) must be a cograph. Hence, in particular, \((G,\sigma )\) cannot contain an induced \(P_4\) on two or three colors (cf. Observation 6). Assume, for contradiction, that \((G,\sigma )\) contains an induced \(P_4\)\(\langle abcd \rangle \) on four distinct colors, where \(\sigma (a)=A\), \(\sigma (b)=B\), \(\sigma (c)=C\), and \(\sigma (d)=D\). By abuse of notation, we will write a, b, c, and d for the \({\mathsf {S} }\)-classes [a], [b], [c], and [d], respectively. Hence, Lemma 5 implies that \((G/{\mathsf {S} },\sigma _{/{\mathsf {S} }})\) contains the induced \(P_4\)\(\langle abcd \rangle \) on four distinct colors. By Observation 6, \(\langle abc\rangle \) must again be an induced \(P_3\) in some connected component \((G_{ABC}^*,\sigma _{ABC}^*)\) of \((G'_{ABC},\sigma '_{ABC})\). Let \(L^*_{ABC}\) be the leaf set of \((G_{ABC}^*,\sigma _{ABC}^*)\). Since \(G_{ABC}^*\notin {\mathcal {P}}_3\) as a consequence of Lemma 22, \((G_{ABC}^*,\sigma _{ABC}^*)\) must contain at least four vertices, i.e., \(|L^*_{ABC}|>3\). Hence, as \((G_{ABC}^*,\sigma _{ABC}^*)\) is of Type (A), Lemma 22 implies that \((G_{ABC}^*,\sigma _{ABC}^*)\) contains a hub-vertex. By Property (A1), the hub-vertex must be connected to any other vertex in \((G_{ABC}^*,\sigma _{ABC}^*)\). Hence, neither a nor c can be the hub-vertex, since \(ac\notin E(G)\). By Corollary 6, the hub-vertex must be the only vertex of its color in \((G_{ABC}^*,\sigma _{ABC}^*)\). Therefore, no vertex of color A or C in \((G_{ABC}^*,\sigma _{ABC}^*)\) can be the hub-vertex. We therefore conclude that the hub-vertex must be b.
Applying the same argumentation to the connected component \((G_{BCD}^*,\sigma _{BCD}^*)\) of \((G'_{BCD},\sigma '_{BCD})\) that contains the induced \(P_3\)\(\langle bcd\rangle \), we can conclude that \(|L^*_{BCD}|>3\) and c must be the hub-vertex of \((G_{BCD}^*,\sigma _{BCD}^*)\). Thus, in particular, it is the only vertex of color C in \((G_{BCD}^*,\sigma _{BCD}^*)\).
Moreover, since \(|L^*_{ABC}|>3\) and b is the only vertex of color B, there must be at least one other vertex of color A or C in the connected component \((G_{ABC}^*,\sigma _{ABC}^*)\).
Assume, for contradiction, that \(L^*_{ABC}\) contains a leaf \(c'\) of color C such that \(c'\ne c\) in \((G_{ABC}^*,\sigma _{ABC}^*)\). Since b is the hub-vertex of \((G_{ABC}^*,\sigma _{ABC}^*)\), we have \(bc'\in E(G_{ABC}^*)\) and thus \(bc'\in E(G)\). As c is the only leaf of color C in \((G_{BCD}^*,\sigma _{BCD}^*)\), we must ensure \(c=c'\) in \(G_{BCD}^*\). Thus, \(cd\in E(G)\) implies \(c'd\in E(G)\). Since \(c\ne c'\) in \(G_{ABC}^*\), c must be adjacent to a vertex \({\tilde{a}}\) of color A that is not adjacent to \(c'\), or vice versa. Suppose first that \({\tilde{a}}c'\in E(G)\) and \({\tilde{a}} c\notin E(G)\). In this case \(a={\tilde{a}}\) in \(G_{ABC}^*\) is possible. Since b is the hub-vertex of \((G_{ABC}^*,\sigma _{ABC}^*)\), we have \({\tilde{a}} b\in E(G)\). Consider \((G'_{ACD},\sigma '_{ACD})\). By construction, the vertices \({\tilde{a}}, c, c',d\) are contained in the same connected component \((G_{ACD}^*,\sigma _{ACD}^*)\) of Type (A) in the 3-RBMG \((G'_{ACD},\sigma '_{ACD})\). Since \({\tilde{a}} c\notin E(G)\), the hub-vertex of \((G_{ACD}^*,\sigma _{ACD}^*)\) must be of color D. Hence, as the hub-vertex is the only vertex of its color in \((G_{ACD}^*,\sigma _{ACD}^*)\), we can conclude that d is the hub-vertex. Therefore, \(\tilde{a}d\in E(G)\), which in particular implies \({\tilde{a}} \ne a\) in \((G_{ACD}^*,\sigma _{ACD}^*)\) because \(ad\notin E(G)\) by assumption. Hence, \(\langle a b {\tilde{a}} d\rangle \in {\mathcal {P}}_4\) in \((G_{ABD}^*,\sigma _{ABD}^*)\); a contradiction. Now assume \({\tilde{a}}c\in E(G)\) and \({\tilde{a}} c'\notin E(G)\). Again, analogous argumentation implies \(\langle a b {\tilde{a}} d\rangle \in {\mathcal {P}}_4\) in \((G^*_{ABD},\sigma _{ABD}^*)\); again a contradiction.
We therefore conclude that \(L^*_{ABC}\) does not contain a leaf \(c'\ne c\) of color C and hence, \(L^*_{ABC}[C]=\{c\}\). Together with \(L^*_{ABC}[B]=\{b\}\) and \(|L^*_{ABC}|>3\), this implies that there must exist a leaf \(a'\ne a\) of color A in \(L^*_{ABC}\). We have \(a'b\in E(G)\) because b is the hub-vertex of \((G_{ABC}^*,\sigma _{ABC}^*)\). Hence, since \((G_{ABC}^*,\sigma _{ABC}^*)\) is \({\mathsf {S} }\)-thin, the neighborhoods of a and \(a'\) must differ. The latter and \(L^*_{ABC}[B] \cup L^*_{ABC}[C]=\{b,c\}\) implies \(a'c\in E(G_{ABC}^*)\), i.e., \(a'c\in E(G)\). One now easily checks that, by \({\mathsf {S} }\)-thinness of \((G^*_{ABC},\sigma ^*_{ABC})\), there cannot be a third vertex of color A in \(L^*_{ABC}\), thus \(L^*_{ABC}=\{a,a',b,c\}\). Applying analogous arguments to \((G_{BCD}^*,\sigma _{BCD}^*)\) shows that \(L^*_{BCD}=\{b,c,d,d'\}\), where \(\sigma (d')=D\) and \(bd', cd'\in E(G)\). Moreover, we have \(a'd\notin E(G)\), because otherwise \(ad,bd\notin E(G)\) would imply that \(\langle aba'd \rangle \) is an induced \(P_4\) in \((G^*_{ABD},\sigma ^*_{ABD})\); a contradiction since \((G^*_{ABD},\sigma ^*_{ABD})\) is of Type (A). Similarly, \(ad'\notin E(G)\) as otherwise \((G^*_{ACD},\sigma ^*_{ACD})\) would contain the induced \(P_4\)\(\langle ad'cd \rangle \).
In summary, \(\langle abcd \rangle \) is an induced \(P_4\) in \((G,\sigma )\) and there are vertices \(a'\) and \(d'\) such that \(a'b,a'c,d'b,d'c\in E(G)\) and \(a'd,ad'\notin E(G)\), see Fig. 14a.
Panel A shows the induced subgraph \((G[L'],\sigma _{|L'})\) with \(L'=\{a,a',b,c,d,d'\}\) of \((G,\sigma )\) that is used in the proof of Theorem 8. In both trees, \(u:={{\,\mathrm{lca}\,}}(b,c)\) and \(v:={{\,\mathrm{lca}\,}}(a,b) = {{\,\mathrm{lca}\,}}(a',b)\). Panel B shows a sketch of the subtree of \((T,\sigma )\) in case \(v \succeq _T u\). Panel C shows a sketch of a possible subtree of \((T,\sigma )\) in case \(v \prec _T u\) and \(w:={{\,\mathrm{lca}\,}}(c,d) = {{\,\mathrm{lca}\,}}(c,d') \prec _T u\). In this representation of \((T,\sigma )\) we have \({{\,\mathrm{lca}\,}}(a,{\widetilde{d}})\succ _T v\) and \({{\,\mathrm{lca}\,}}({\widetilde{a}},d)\succ _T w\). However, \({{\,\mathrm{lca}\,}}(a,{\widetilde{d}})\preceq _T v\) or \({{\,\mathrm{lca}\,}}({\widetilde{a}},d)\preceq _T w\) may be possible. Dashed lines represent edges in \((G[L'],\sigma _{|L'})\) and paths in the trees that may or may not be present. Solid lines in the trees represent paths (color figure online)
Let \((T,\sigma )\) be a tree that explains \((G,\sigma )\) and \(u:={{\,\mathrm{lca}\,}}(b,c)\). The steps of the subsequent proof are illustrated in Fig. 14. Since \(ab \in E(G)\), we have \({{\,\mathrm{lca}\,}}(a,b) \preceq _T {{\,\mathrm{lca}\,}}(a',b)\). Similarly, \(a'b\in E(G)\) implies \({{\,\mathrm{lca}\,}}(a',b) \preceq _T {{\,\mathrm{lca}\,}}(a,b)\). Hence, we clearly have \(v:={{\,\mathrm{lca}\,}}(a,b) = {{\,\mathrm{lca}\,}}(a',b)\). Note, v and u are both ancestors of b and are thus located on the path from the root \(\rho _T\) to b. In other words, v and u are always comparable in T, i.e., we have either \(v\succeq _T u\) or \(v\prec _T u\). If \(v\succeq _T u\), then \(v={{\,\mathrm{lca}\,}}(a,c)={{\,\mathrm{lca}\,}}(a',c)\). Since \(a'c\in E(G)\), we have \(v \preceq _T {{\,\mathrm{lca}\,}}(a',{\widetilde{c}})\) and \(v\preceq _T {{\,\mathrm{lca}\,}}({\widetilde{a}}, c)\) for all \(\widetilde{a} \in L[A]\) and all \(\widetilde{c} \in L[C]\). Together with \(v={{\,\mathrm{lca}\,}}(a,c)\), this implies \(ac\in E(G)\); a contradiction. Thus, only the case \(v\prec _T u\) is possible and hence, v must be located on the path from some child of u to b in T. Similarly, we have \(w:={{\,\mathrm{lca}\,}}(c,d) = {{\,\mathrm{lca}\,}}(c,d')\) because \(cd,cd'\in E(G)\). As \(bd'\in E(G)\), \(bd\notin E(G)\), we can apply an analogous argumentation as for u and v to conclude that only the case \(w\prec _T u\) is possible. Thus w must be located on the path from some child of u to c in T. In particular, we have \({{\,\mathrm{lca}\,}}(v,w)=u\) by definition of u and therefore, \(u={{\,\mathrm{lca}\,}}(a,d)\). Since \(ad\notin E(G)\), we have \(u={{\,\mathrm{lca}\,}}(a,d)\succ _T {{\,\mathrm{lca}\,}}(a,{\widetilde{d}})\) for some \({\widetilde{a}}\in L[A]\) or \(u={{\,\mathrm{lca}\,}}(a,d)\succ _T {{\,\mathrm{lca}\,}}({\widetilde{a}},d)\) for some \({\widetilde{d}}\in L[D]\). Assume that \(u={{\,\mathrm{lca}\,}}(a,d)\succ _T {{\,\mathrm{lca}\,}}(a,{\widetilde{d}})\) for some \({\widetilde{d}}\in L[D]\). In this case, \({{\,\mathrm{lca}\,}}(a,{\widetilde{d}})\) must be located on the path from some child \(u'\) of u to a. Thus, \(u \succ _T u'\succ _T a,{\widetilde{d}}\) and by construction, \(u'\succ _T b\). Hence, \({{\,\mathrm{lca}\,}}(b,{\widetilde{d}}) \prec _T u = {{\,\mathrm{lca}\,}}(b,d')\) and thus \(bd'\notin E(G)\); a contradiction. Analogously, \(u={{\,\mathrm{lca}\,}}(a,d)\succ _T {{\,\mathrm{lca}\,}}({\widetilde{a}}, d)\) would imply that \({{\,\mathrm{lca}\,}}({\widetilde{a}}, d)\) is located on the path from some child of u to d, which would contradict \(a'c\in E(G)\). Therefore, the tree \((T,\sigma )\) does not explain \((G,\sigma )\); a contradiction.
Thus, if for any distinct colors r, s, t, each 3-colored connected component \((G_{rst}^*,\sigma _{rst}^*)\) of \((G'_{rst},\sigma '_{rst})\) is a 3-RBMG of Type (A), then \((G,\sigma )\) must be a cograph. \(\square \)
As a result of the previous proof, the induced subgraph shown in Panel a of Fig. 14 is a forbidden subgraph of general RBMGs.
1.3 Hierarchically colored cographs
Definition 20
A graph that is both a cograph and an RBMG is a co-RBMG.
Lemma 41
Let \((G,\sigma )\) be a co-RBMG that is a explained by \((T,\sigma )\). Then, for any \(v\in V^0(T)\) and each pair of distinct children \(w_1,w_2\in \mathsf {child} _T(v)\), the sets \(\sigma (L(T(w_1)))\) and \(\sigma (L(T(w_2)))\) do not overlap.
Proof
Assume, for contradiction, that there exists some \(v\in V^0(T)\) and distinct \(w_1,w_2 \in \mathsf {child} (v)\) such that \(r\in \sigma (L(T(w_1)))\cap \sigma (L(T(w_2)))\), s is contained in \(\sigma (L(T(w_1)))\) but not in \(\sigma (L(T(w_2)))\), and t is contained in \(\sigma (L(T(w_2)))\) but not in \(\sigma (L(T(w_1)))\) for three distinct colors r, s, t in \((G,\sigma )\). Then, by Corollary 2, there is a pair \(x,y\in L(T(w_1))\) with \(\sigma (x)=r\), \(\sigma (y)=s\), and \(xy\in E(G)\), as well as a pair \(x',z\in L(T(w_2))\) with \(\sigma (x')=r, \sigma (z)=t\) and \(x'z\in E(G)\). Since \(t\notin \sigma (L(T(w_1)))\) and \(s\notin \sigma (L(T(w_2)))\), we have \({{\,\mathrm{lca}\,}}_T(y,z)=v\preceq _T {{\,\mathrm{lca}\,}}_T(y,z')\) for any \(z'\in L[t]\) and \({{\,\mathrm{lca}\,}}_T(y,z)=v\preceq _T {{\,\mathrm{lca}\,}}_T(y',z)\) for any \(y'\in L[s]\), hence \(yz\in E(G)\). Moreover, as \({{\,\mathrm{lca}\,}}_T(z,x')\prec _T v={{\,\mathrm{lca}\,}}_T(z,x)\) and \({{\,\mathrm{lca}\,}}_T(y,x)\prec _T v={{\,\mathrm{lca}\,}}_T(y,x')\), the edges xz and \(x'y\) are not contained in \((G,\sigma )\). We therefore conclude that \(\langle xyzx'\rangle \) is an induced \(P_4\) in \((G,\sigma )\); a contradiction since \((G,\sigma )\) is a cograph. \(\square \)
Definition 21
Let \((H_1,\sigma _{H_1})\) and \((H_2,\sigma _{H_2})\) be two vertex-disjoint colored graphs. Then \((H_1,\sigma _{H_1}) {{\,\mathrm{\triangledown }\,}}(H_2,\sigma _{H_2}) :=(H_1{{\,\mathrm{\triangledown }\,}}H_2,\sigma )\) and  denotes their join and union, respectively, where \(\sigma (x) = \sigma _{H_i}(x)\) for every \(x\in V(H_i)\), \(i\in \{1,2\}\).
denotes their join and union, respectively, where \(\sigma (x) = \sigma _{H_i}(x)\) for every \(x\in V(H_i)\), \(i\in \{1,2\}\).
Lemma 42
Let \((G,\sigma )\) be a properly colored undirected graph such that either \((G,\sigma )=(H,\sigma _H) {{\,\mathrm{\triangledown }\,}}(H',\sigma _{H'})\) with \(\sigma (V(H))\cap \sigma (V(H'))=\emptyset \) or  with \(\sigma (V(H))\cap \sigma (V(H')) \in \{\sigma (V(H)),\sigma (V(H'))\}\), where \((H,\sigma _H)\) and \((H',\sigma _{H'})\) are disjoint RBMGs. Then, \((G,\sigma )\) is an RBMG.
with \(\sigma (V(H))\cap \sigma (V(H')) \in \{\sigma (V(H)),\sigma (V(H'))\}\), where \((H,\sigma _H)\) and \((H',\sigma _{H'})\) are disjoint RBMGs. Then, \((G,\sigma )\) is an RBMG.
Moreover, let \((H,\sigma _H)\) and \((H',\sigma _{H'})\) be explained by the trees \((T_H, \sigma _H)\) and \((T_{H'}, \sigma _{H'})\), respectively and let \((T,\sigma )\) be the tree obtained by joining \((T_H,\sigma _H)\) and \((T_{H'},\sigma _{H'})\) by a common root \(\rho _T\). Then \((T,\sigma )\) explains \((G,\sigma )\).
Proof
Let \((T,\sigma )\) be the tree that is obtained by joining \((T_H, \sigma _H)\) and \((T_{H'}, \sigma _{H'})\) with roots \(\rho _{H}\) and \(\rho _{H'}\), respectively, under a common root \(\rho _T\). By construction, \(\sigma (V(H)) = \sigma _H\) and \(\sigma (V(H')) = \sigma _{H'}\). We first show that \((T(\rho _H),\sigma _H)\) and \((T(\rho _{H'}),\sigma _{H'})\) explain \((H,\sigma _H)\) and \((H',\sigma _{H'})\), respectively. By construction, we have \({{\,\mathrm{lca}\,}}_T(x,y)={{\,\mathrm{lca}\,}}_{T_H}(x,y)\) and \({{\,\mathrm{lca}\,}}_T(x,y)\prec _T {{\,\mathrm{lca}\,}}_T(x,z)\) for any \(x,y\in V(H)\) and \(z\in V(H')\). It is therefore easy to see that \(G(T(\rho _H),\sigma _H)=(H,\sigma _H)\). Analogous arguments show \(G(T(\rho _{H'}),\sigma _{H'})=(H',\sigma _{H'})\). Therefore, in order to show that \((T,\sigma )\) explains \((G,\sigma )\), it remains to show that all edges between vertices in V(H) and \(V(H')\) are identical in \((G,\sigma )\) and \(G(T,\sigma )\).
Suppose first \((G,\sigma )=(H,\sigma _H){{\,\mathrm{\triangledown }\,}}(H',\sigma _{H'})\) with \(\sigma (V(H))\cap \sigma (V(H'))=\emptyset \). Thus we need to show \(xy\in E(G(T,\sigma ))\) for any \(x\in L(T(\rho _H)), y\in L(T(\rho _{H'}))\). Since \(\sigma (V(H))\) and \(\sigma (V(H'))\) form a partition of \(\sigma (V(G))\), we have \({{\,\mathrm{lca}\,}}_T(x,y)=\rho _T\) for any \(x\in L[r], y\in L[s]\) with \(r \in \sigma (V(H))\) and \(s\in \sigma (V(H'))\). Hence, \(xy\in E(G(T,\sigma ))\) for any \(x\in L(T(\rho _H)), y\in L(T(\rho _{H'}))\) and therefore, \(G(T,\sigma )=(G,\sigma )\).
Now suppose that  with \(\sigma (V(H))\cap \sigma (V(H')) \in \{\sigma (V(H)),\sigma (V(H'))\}\). Thus, we need to show \(xy\notin E(G(T,\sigma ))\) for any \(x\in L(T(\rho _H)), y\in L(T(\rho _{H'}))\). W.l.o.g. assume \(\sigma (V(H'))\subseteq \sigma (V(H))\). Hence, \((T(\rho _H),\sigma _H)\) is color-complete. We can therefore apply Lemma 13 to conclude that \(xy\notin E(G(T,\sigma ))\) for any \(x\in V(H), y\in V(H')\). Hence, \(G(T,\sigma )=(G,\sigma )\). \(\square \)
with \(\sigma (V(H))\cap \sigma (V(H')) \in \{\sigma (V(H)),\sigma (V(H'))\}\). Thus, we need to show \(xy\notin E(G(T,\sigma ))\) for any \(x\in L(T(\rho _H)), y\in L(T(\rho _{H'}))\). W.l.o.g. assume \(\sigma (V(H'))\subseteq \sigma (V(H))\). Hence, \((T(\rho _H),\sigma _H)\) is color-complete. We can therefore apply Lemma 13 to conclude that \(xy\notin E(G(T,\sigma ))\) for any \(x\in V(H), y\in V(H')\). Hence, \(G(T,\sigma )=(G,\sigma )\). \(\square \)
Definition 22
An undirected colored graph \((G,\sigma )\) is a hierarchically colored cograph (hc-cograph) if
- (K1)
\((G,\sigma )=(K_1,\sigma )\), i.e., a colored vertex, or
- (K2)
\((G,\sigma )= (H,\sigma _H) {{\,\mathrm{\triangledown }\,}}(H',\sigma _{H'})\) and \(\sigma (V(H))\cap \sigma (V(H'))=\emptyset \), or
- (K3)
 and \(\sigma (V(H))\cap \sigma (V(H')) \in \{\sigma (V(H)),\sigma (V(H'))\}\),
and \(\sigma (V(H))\cap \sigma (V(H')) \in \{\sigma (V(H)),\sigma (V(H'))\}\),
where both \((H,\sigma _H)\) and \((H',\sigma _{H'})\) are hc-cographs. For the color-constraints (cc) in (K2) and (K3), we simply write (K2cc) and (K3cc), respectively.
Omitting the color-constraints reduces Definition 22 to Definition 4. Therefore we have
Observation 9
If \((G,\sigma )\) is an hc-cograph, then G is cograph.
The recursive construction of an hc-cograph \((G,\sigma )\) according to Definition 22 immediately produces a binary hc-cotree \(T^G_{hc }\) corresponding to \((G,\sigma )\). The construction is essentially the same as for the cotree of a cograph [cf. Corneil et al. (1981, Section 3)]: Each of its inner vertices is labeled by 1 for a \({{\,\mathrm{\triangledown }\,}}\) operation and 0 for a disjoint union  , depending on whether (K2) or (K3) is used in the construction steps. We write \(t:V^0(T^G_{hc })\rightarrow \{0,1\}\) for the labeling of the inner vertices. By construction, \((T^G_{hc },t)\) is a not necessarily discriminating cotree for G, see 9. The relationships of hc-cographs and their corresponding hc-cotrees are described at length in the main text.
, depending on whether (K2) or (K3) is used in the construction steps. We write \(t:V^0(T^G_{hc })\rightarrow \{0,1\}\) for the labeling of the inner vertices. By construction, \((T^G_{hc },t)\) is a not necessarily discriminating cotree for G, see 9. The relationships of hc-cographs and their corresponding hc-cotrees are described at length in the main text.
Lemma 43
Every hc-cograph \((G,\sigma )\) is a properly colored cograph.
Proof
Let \((G,\sigma )\) be an hc-cograph. In order to see that \((G,\sigma )\) is properly colored, observe that any edge xy in \((G,\sigma )\) must be the result of some (possible preceding) join \((H,\sigma _H){{\,\mathrm{\triangledown }\,}}(H',\sigma _{H'})\) during the recursive construction of \((G,\sigma )\) such that \(x\in V(H)\) and \(y\in V(H')\). Condition (K2) implies that \(\sigma (V(H))\cap \sigma (V(H'))=\emptyset \) and hence, \(\sigma (x)\ne \sigma (y)\) for every edge xy in \((G,\sigma )\). \(\square \)
Theorem 9
A vertex labeled graph \((G,\sigma )\) is a co-RBMG if and only if it is an hc-cograph.
Proof
Suppose that \((G,\sigma )\) with vertex set V and edge set E is a co-RBMG. We show by induction on |V| that \((G,\sigma )\) is an hc-cograph. This is trivially true in the base case \(|V|=1\).
For the induction step assume that any co-RBMG with less than N vertices is at the same time an hc-cograph and consider a co-RBMG with \(|V|=N\). Since \((G,\sigma )\) is an n-RBMG, there exists a tree \((T,\sigma )\) with root \(\rho _T\) that explains \((G,\sigma )\). By Lemma 41, none of the color sets \(\sigma (L(T(v)))\) and \(\sigma (L(T(w)))\) overlap for any two children \(v,w\in \mathsf {child} (\rho _T)\). Moreover, Lemma 41 allows us to define a partition \({\varPi }\) of \(\mathsf {child} (\rho _T)\) into classes \(P_1,\dots ,P_k\) such that each pair of vertices \(v\in P_i\) and \(w\in P_j\), \(i\ne j\) satisfies \(\sigma (L(T(v))) \cap \sigma (L(T(w))) = \emptyset \). Note that each \(P_i\) may contain distinct elements v, w such that \(\sigma (L(T(v))) \cap \sigma (L(T(w))) \in \{\emptyset , \sigma (L(T(v))), \sigma (L(T(w))) \}\).
First assume that the partition \({\varPi }\) of \(\mathsf {child} (\rho _T)\) is trivial, i.e., it consists of a single class \(P_1\). Since none of the sets \(\sigma (L(T(v)))\) and \(\sigma (L(T(w)))\) overlap for any \(v,w\in P_1\), there is an element \(w\in P_1\) such that \(\sigma (L(T(w)))\) is inclusion-maximal, i.e., \(\sigma (L(T(v))) \subseteq \sigma (L(T(w)))\) for all \(v\in P_1=\mathsf {child} (\rho _T)\). Let \(L_{\lnot w}= \bigcup _{v\in P_1{\setminus } w} L(T(v))\) and \(L_w = L(T(w))\). Since \(\rho _T\) is always color-complete, w must be color-complete, i.e., \(\sigma (L_w) = \sigma (V)\). Hence, we have \(\sigma (L_{\lnot w}) \subseteq \sigma (L_w)\).
We continue by showing that \((G[L_{\lnot w}], \sigma _{|L_{\lnot w}})\) and \((G[L_w],\sigma _{|L_{w}})\) are RBMGs that are explained by \((T_{|L_{\lnot w}}, \sigma _{|L_{\lnot w}})\) and \((T_{|L_{w}}, \sigma _{|L_{w}})\), respectively. By construction, we have \({{\,\mathrm{lca}\,}}_T(x,y)={{\,\mathrm{lca}\,}}_{T_{|L_{\lnot w}}}(x,y)\) and \({{\,\mathrm{lca}\,}}_T(x,y)\preceq _T {{\,\mathrm{lca}\,}}_T(x,z)\) for any \(x,y\in L_{\lnot w}\) and \(z\in L_w\). It is therefore easy to see that \(G(T_{|L_{\lnot w}},\sigma _{|L_{\lnot w}})=(G[L_{\lnot w}],\sigma _{|L_{\lnot w}})\). Analogous arguments show that \(G(T_{|L_{w}},\sigma _{|L_{w}})=(G[L_{w}],\sigma _{|L_{w}})\). Hence, \((G[L_{\lnot w}], \sigma _{|L_{\lnot w}})\) and \((G[L_w],\sigma _{|L_{w}})\) are RBMGs. Since any induced subgraph of a cograph is again a cograph, we can thus conclude that \((G[L_{\lnot w}], \sigma _{|L_{\lnot w}})\) and \((G[L_w],\sigma _{|L_{w}})\) are co-RBMGs. Hence, by induction hypothesis, \((G[L_{\lnot w}], \sigma _{|L_{\lnot w}})\) and \((G[L_w],\sigma _{|L_{w}})\) are hc-cographs. Moreover, since w is color-complete, we can apply Lemma 13 to conclude that  is the disjoint union of two hc-cographs and in addition satisfies \(\sigma (L_{\lnot w}) \subseteq \sigma (L_w)\). Hence, \((G,\sigma )\) satisfies Property (K3) and is therefore an hc-cograph.
is the disjoint union of two hc-cographs and in addition satisfies \(\sigma (L_{\lnot w}) \subseteq \sigma (L_w)\). Hence, \((G,\sigma )\) satisfies Property (K3) and is therefore an hc-cograph.
Now assume that \({\varPi }\) is non-trivial, i.e., there are at least two classes \(P_1,\dots ,P_k\). Then, by construction, we have \(\sigma (L(T(v))) \cap \sigma (L(T(w))) = \emptyset \) for all \(v\in P_i\) and \(w\in P_j\), \(i\ne j\). Let \(L_i = \bigcup _{v\in P_i} L(T(v))\). By construction, \(\sigma (L_i)\cap \sigma (L_j) = \emptyset \) for all distinct i, j. Hence, \(\sigma (L_1), \dots , \sigma (L_k)\) form a partition of \(\sigma (V)\). Thus, we have \({{\,\mathrm{lca}\,}}_T(x,y)=\rho _T\) for any \(x\in L[r], y\in L[s]\) with \(r \in \sigma (L_i)\) and \(s\in \sigma (L_j)\) for distinct \(i,j\in \{1,\dots ,k\}\), which clearly implies \(xy\in E(G)\). Hence, \(G=G[L_1]{{\,\mathrm{\triangledown }\,}}G[L_2] {{\,\mathrm{\triangledown }\,}}\cdots {{\,\mathrm{\triangledown }\,}}G[L_k]\). Thus, by setting \(H = {{\,\mathrm{\triangledown }\,}}_{i=1}^{k-1} G[L_i]\) and \(H'=G[L_k]\), we obtain \((G,\sigma ) = (H,\sigma _{|V(H)}){{\,\mathrm{\triangledown }\,}}(H',\sigma _{|V(H')})\). We proceed to show that \((H,\sigma _{|V(H)})\) and \((H',\sigma _{|V(H')})\) are hc-cographs. Since any induced subgraph of a cograph is again a cograph, we can conclude that H and \(H'\) are cographs. Thus it remains to show that \((H,\sigma _{|V(H)})\) and \((H',\sigma _{|V(H')})\) are RBMGs. By similar arguments as in the case for one class \(P_1\), one shows that \((T_{|V(H)}, \sigma _{|V(H)})\) and \((T_{|V(H')}, \sigma _{|V(H')})\) explain \((H,\sigma _{|V(H)})\) and \((H',\sigma _{|V(H')})\), respectively. In summary, \((H,\sigma _{|V(H)})\) and \((H',\sigma _{|V(H')})\) are co-RBMGs and thus, by induction hypothesis, hc-cographs. Since \(\sigma (V(H)) = \bigcup _{i=1}^{k-1} \sigma (L_i)\), \(\sigma (V(H')) = \sigma (L_k)\), and \(\sigma (L_i), \sigma (L_j)\) are disjoint for distinct \(i,j\in \{1,\dots ,k\}\), we can conclude that \(\sigma (V(H)) \cap \sigma (V(H')) = \emptyset \). Hence, \((G,\sigma ) = (H,\sigma _{|V(H)}) {{\,\mathrm{\triangledown }\,}}(H',\sigma _{|V(H')})\) satisfies Property (K2). Thus \((G,\sigma )\) is an hc-cograph.
Now suppose that \((G=(V,E),\sigma )\) is an hc-cograph. Lemma 43 implies that G is a cograph. In order to show that \((G,\sigma )\) is an RBMG, we proceed again by induction on |V|. The base case \(|V|=1\) is trivially satisfied. For the induction hypothesis, assume that any hc-cograph \((G,\sigma )\) with \(|V|<N\) is an RBMG. Now let \((G,\sigma )\) with \(|V|=N>1\) be an hc-cograph. By definition of hc-cographs and since \(|V|>1\), there exist disjoint hc-cographs \((H,\sigma _H)\) and \((H',\sigma _{H'})\) such that either (i) \((G,\sigma )=(H,\sigma _{H}) {{\,\mathrm{\triangledown }\,}}(H',\sigma _{H'})\) and \(\sigma (V(H)) \cap \sigma (V(H'))=\emptyset \) or (ii)  and \(\sigma (V(H)) \cap \sigma (V(H'))\in \{\sigma (V(H)), \sigma (V(H'))\}\). By induction hypothesis, \((H,\sigma (V(H)))\) and \((H',\sigma (V(H')))\) are RBMGs. Hence, we can apply Lemma 42 to conclude that \((G,\sigma )\) an RBMG. \(\square \)
and \(\sigma (V(H)) \cap \sigma (V(H'))\in \{\sigma (V(H)), \sigma (V(H'))\}\). By induction hypothesis, \((H,\sigma (V(H)))\) and \((H',\sigma (V(H')))\) are RBMGs. Hence, we can apply Lemma 42 to conclude that \((G,\sigma )\) an RBMG. \(\square \)
Theorem 10
Every co-RBMG \((G,\sigma )\) is explained by its cotree \((T^G_{hc },\sigma )\).
Proof
We show by induction on |V| that \((G,\sigma )\) is explained by \((T^G_{hc },\sigma )\). This is trivially true for the base case \(|V|=1\). Assume that any co-RBMG with less than N vertices is explained by its cotree \((T^G_{hc },\sigma )\). Now let \((G=(V,E),\sigma )\) be a co-RBMG with \(|V|= N\). By Theorem 9, \((G,\sigma )\) is an hc-cograph. Thus, \((G,\sigma )= (H,\sigma _H) \star (H',\sigma _{H'})\),  such that (K2) and (K3), resp., are satisfied. Theorem 9 implies that \((H,\sigma _H)\) and \((H',\sigma _{H'})\) are co-RBMGs. By induction hypothesis, the co-RBMGs \((H,\sigma _H)\) and \((H',\sigma _{H'})\) are explained by their hc-cotrees \((T^H_{hc },\sigma _H)\) and \((T^{H'}_{hc },\sigma _{H'})\), respectively. By construction, \((T^G_{hc },\sigma )\) is the tree that is obtained by joining \((T^H_{hc },\sigma _H)\) and \((T^{H'}_{hc },\sigma _{H'})\) under a common root. Lemma 42 now implies that the \((T^G_{hc },\sigma )\) explains \((G,\sigma )\). \(\square \)
such that (K2) and (K3), resp., are satisfied. Theorem 9 implies that \((H,\sigma _H)\) and \((H',\sigma _{H'})\) are co-RBMGs. By induction hypothesis, the co-RBMGs \((H,\sigma _H)\) and \((H',\sigma _{H'})\) are explained by their hc-cotrees \((T^H_{hc },\sigma _H)\) and \((T^{H'}_{hc },\sigma _{H'})\), respectively. By construction, \((T^G_{hc },\sigma )\) is the tree that is obtained by joining \((T^H_{hc },\sigma _H)\) and \((T^{H'}_{hc },\sigma _{H'})\) under a common root. Lemma 42 now implies that the \((T^G_{hc },\sigma )\) explains \((G,\sigma )\). \(\square \)
1.4 Recognition of hc-cographs
Although (discriminating) cotrees can be constructed and cographs can be recognized in linear time (Habib and Paul 2005; Bretscher et al. 2008; Corneil et al. 1985), these results cannot be applied directly to the construction of hc-cotrees and the recognition of hc-cographs. The key problem is that whenever \((G,\sigma )\) comprises \(k>2\) connected components, there are \(2^{k-1}-1\) bipartitions  . For each of them (K3cc) needs to be checked, and if it is satisfied, both \(G_1\) and \(G_2\) need to be tested for being hc-cotrees. In general, this incurs exponential effort. The following results show, however, that it suffices to consider a single, carefully chosen bipartition for each disconnected graph \((G,\sigma )\).
. For each of them (K3cc) needs to be checked, and if it is satisfied, both \(G_1\) and \(G_2\) need to be tested for being hc-cotrees. In general, this incurs exponential effort. The following results show, however, that it suffices to consider a single, carefully chosen bipartition for each disconnected graph \((G,\sigma )\).
Lemma 44
Every connected component of an hc-cograph is an hc-cograph.
Proof
Let \((G,\sigma )\) be an hc-cograph. By Theorem 9, \((G,\sigma )\) is a co-RBMG. Since each connected component of a cograph is again a cograph, each connected component of \((G,\sigma )\) must be a cograph. In addition, Theorem 3 implies that each connected component of \((G,\sigma )\) is an RBMG. The latter two arguments imply that each connected component of \((G,\sigma )\) is a co-RBMG. Hence, Theorem 9 implies that each connected component of \((G,\sigma )\) is an hc-cograph. \(\square \)
Lemma 45
Let \((G,\sigma )\) be a disconnected hc-cograph with connected components \(G_{1}=(V_1,E_1)\), ..., \(G_k=(V_k,E_k)\) and let \(G_{\ell }\), \(1\le \ell \le k\) be a connected component whose color set is minimal w.r.t. inclusion, i.e., there is no \(i\in \{1,\dots ,k\}\) with \(i\ne \ell \) such that \(\sigma (V_{i}) \subsetneq \sigma (V_{\ell })\). Denote by \(G-G_{\ell }\) the graph obtained from \((G,\sigma )\) by deleting the connected component \(G_{\ell }\). Then

satisfies Property (K3).
Proof
Let \((G=(V,E),\sigma )\) be a disconnected hc-cograph with connected components \((G_{1} = (V_1,E_1),\sigma _1), \dots , (G_k=(V_k,E_k),\sigma _k)\) and put \(\sigma _i:=\sigma _{|V_i}\), \(1\le i\le k\). Let \((G_{\ell },\sigma _{\ell })\), \(1\le \ell \le k\) be a graph such that \(\sigma (V_{\ell })\) is minimal w.r.t. inclusion. We write \(G'=(V',E'):=G - G_{\ell }\) and \(\sigma ':=\sigma _{|V{\setminus } V_{\ell }}\), thus \((G', \sigma ') = (G- G_{\ell },\sigma _{|V{\setminus } V_{\ell }})\) and \(V'=V{\setminus } V_{\ell }\). In order to prove that  satisfies (K3), we must show (i) that \((G_{\ell },\sigma _{\ell })\) and \((G', \sigma ')\) are hc-cographs and (ii) that \(\sigma (V_{\ell }) \cap \sigma (V') \in \{\sigma (V_{\ell }), \sigma (V') \}\).
satisfies (K3), we must show (i) that \((G_{\ell },\sigma _{\ell })\) and \((G', \sigma ')\) are hc-cographs and (ii) that \(\sigma (V_{\ell }) \cap \sigma (V') \in \{\sigma (V_{\ell }), \sigma (V') \}\).
(i) By Lemma 44, each connected component \((G_{1},\sigma _1), \dots , (G_k,\sigma _k)\) is an hc-cograph. Thus, in particular, \((G_{\ell },\sigma _{\ell })\) is an hc-cograph. Furthermore, Theorem 9 implies that each connected component \((G_{1},\sigma _1), \dots , (G_k,\sigma _k)\) is a co-RBMG. By Theorem 3, the latter two arguments imply that \((G', \sigma ')\) is a co-RBMG. Moreover, Theorem 3 implies that there exists \(1\le j\le k\) such that \(\sigma (V_j)=\sigma (V)\) and \(j\ne l\) since \(\sigma (V_l)\) is minimal w.r.t. inclusion.
(ii) By Theorem 9, \((G,\sigma )\) is an RBMG. Applying Corollary 3, we can conclude that \((G,\sigma )\) contains a connected component \((G^*,\sigma ^*)\) with \(\sigma (V(G^*))=\sigma (V)\). Since \(\sigma (V_{\ell })\) is minimal w.r.t. inclusion, we can w.l.o.g. assume that \((G^*,\sigma ^*)\) is contained in \((G',\sigma ')\). Hence, \(\sigma (V_{\ell })\cap \sigma (V')=\sigma (V_{\ell })\cap \sigma (V)=\sigma (V_{\ell })\) and thus, \(\sigma (V_{\ell })\subseteq \sigma (V')\), which implies that  satisfies Property (K3cc). \(\square \)
satisfies Property (K3cc). \(\square \)
The choice of the graph \(G_{\ell }\) in Lemma 45 will in general not be unique. As a consequence, there may be distinct cotrees \((T_{hc }^G,\sigma )\) that explain the same co-RBMG, see Fig. 9 for an illustrative example.
While Theorem 8 allows the recognition of co-RBMGs in polynomial time, it does not provide an explaining tree. The equivalence of co-RBMGs and hc-cographs together with Lemmas 42 and 45 yields an alternative polynomial-time recognition algorithm that is constructive in the sense that it explicitly provides a tree explaining \((G,\sigma )\).
Theorem 11
Let \((G,\sigma )\) be a properly colored undirected graph. Then it can be decided in polynomial time whether \((G,\sigma )\) is a co-RBMG and, in the positive case, a tree \((T,\sigma )\) that explains \((G,\sigma )\) can be constructed in polynomial time.
Proof
Let \({{\overline{G}}}\) denote the complement of G. Testing if \((G,\sigma )\) is the join or disjoint union of graphs can clearly be done in polynomial time.
Assume first that \((G,\sigma )\) is the join of graphs. In this case, \(({{\overline{G}}},\sigma )\) decomposes into connected components \(({{\overline{G}}}_1,\sigma _1),\dots , ({{\overline{G}}}_k,\sigma _k)\), \(k\ge 2\), i.e.,  . Therefore,
. Therefore,  , where none of the graphs \((G_i,\sigma _i)\) can be written as the join of two graphs and k is maximal. Note, we can ignore the parenthesis in the latter equation, since the \({{\,\mathrm{\triangledown }\,}}\) operation is associative. It follows from (K2cc) that \((G,\sigma )\) is an hc-cograph if and only if (1) all \((G_i,\sigma _i)\) are hc-cographs and (2) all color sets \(\sigma (V(G_i))\) are pairwise disjoint. In this case, every binary tree with leaves \((G_1,\sigma _1),\dots , (G_k,\sigma _k)\) and all inner vertices labeled 1 may appear in \((T^G_{hc},t)\).
, where none of the graphs \((G_i,\sigma _i)\) can be written as the join of two graphs and k is maximal. Note, we can ignore the parenthesis in the latter equation, since the \({{\,\mathrm{\triangledown }\,}}\) operation is associative. It follows from (K2cc) that \((G,\sigma )\) is an hc-cograph if and only if (1) all \((G_i,\sigma _i)\) are hc-cographs and (2) all color sets \(\sigma (V(G_i))\) are pairwise disjoint. In this case, every binary tree with leaves \((G_1,\sigma _1),\dots , (G_k,\sigma _k)\) and all inner vertices labeled 1 may appear in \((T^G_{hc},t)\).
Now assume that \((G,\sigma )\) is the disjoint union of the connected graphs \((G_i,\sigma _i)\), \(1\le i\le k\). Let \(G_{\ell } = (V_{\ell },E_{\ell })\), \(1\le \ell \le k\) be a connected component such that \(\sigma (V_{\ell })\) is minimal w.r.t. inclusion. Such a component can be clearly identified in polynomial time. By Lemma 45,  satisfies (K3), whenever \((G,\sigma )\) is a co-RBMG. Again, Lemma 42 implies that the two trees that explains \((G_{\ell },\sigma _{|V_{\ell }})\) and \((G-G_{\ell },\sigma _{|V{\setminus } V_{\ell }})\), respectively, can then be joined under a common root in order to obtain a tree that explains \((G,\sigma )\). The effort is again polynomial.
satisfies (K3), whenever \((G,\sigma )\) is a co-RBMG. Again, Lemma 42 implies that the two trees that explains \((G_{\ell },\sigma _{|V_{\ell }})\) and \((G-G_{\ell },\sigma _{|V{\setminus } V_{\ell }})\), respectively, can then be joined under a common root in order to obtain a tree that explains \((G,\sigma )\). The effort is again polynomial.
Finally, each of the latter steps must be repeated recursively on the connected components of either G or \({\overline{G}}\). This either results in an hc-cotree \((T^G_{hc },t,\sigma )\) or we encounter a violation of (K2cc) or (K3cc) on the way. That is, we obtain a join decomposition such that the color sets \(\sigma (V(G_i))\) are not pairwise disjoint, or a graph \(G_{\ell }\) such that  violates (K3cc). In either case, the recursion terminates and reports “\((G,\sigma )\) is not an hc-cograph”. Since \(T^G_{hc }\) has O(|V(G)|) vertices, the polynomial-time decomposition steps must be repeated at most O(|V(G)|) times, resulting in an overall polynomial-time algorithm. \(\square \)
violates (K3cc). In either case, the recursion terminates and reports “\((G,\sigma )\) is not an hc-cograph”. Since \(T^G_{hc }\) has O(|V(G)|) vertices, the polynomial-time decomposition steps must be repeated at most O(|V(G)|) times, resulting in an overall polynomial-time algorithm. \(\square \)
Recall that \(T_e\) denotes the tree that is obtained from T by contraction of the edge e and \((T,t,\sigma )\) or (T, t) is a cotree for \((G,\sigma )\) if \(t({{\,\mathrm{lca}\,}}(x, y))=1\) if and only if \(xy \in E(G)\).
The cotree \((T,t,\sigma )\) explains a 4-colored co-RBMG \((G,\sigma )\). Corollary 10 implies that the edge uv is redundant. However, by Proposition 1, the tree \((T_e,t')\) is not a cotree for the co-RBMG \((G,\sigma )\) for all possible labelings \(t':V^0(T)\rightarrow \{0,1\}\). Moreover, Lemma 46(2) implies that the two inner edges \(vw_3\) and \(vw_4 \) of T are redundant. However, contracting both edges at the same time gives a tree \((T_1,\sigma )\) with \(\mathsf {par} (a_2)=\mathsf {par} (a_3)\), thus \(a_2\) and \(a_3\) belong to the same \({\mathsf {S} }\)-class in \(G(T_1,\sigma )\). Hence, \((T_1,\sigma )\) does not explain \((G,\sigma )\) (cf. Lemma 48). Finally, one checks that the edge \(vw_1\) is relevant because the edge \(a_3c_2\) is contained in \(G(T_2,\sigma )\), where \((T_2,\sigma )\) is obtained from \((T,\sigma )\) by contraction of \(vw_1\), but not in \((G,\sigma )\) (cf. Lemma 46) (color figure online)
Figure 2 gives an example of a least resolved tree \((T,\sigma )\) that explains a co-RBMG \((G,\sigma )\). However, one easily verifies that \((T,\sigma )\) is not a refinement of the discriminating cotree for \((G,\sigma )\). Moreover, as shown in Fig. 9, there might exist several cotrees that explain a given co-RBMG. By Proposition 1, the discriminating cotree for a co-RBMG \((G,\sigma )\) is unique. It does not necessarily explain \((G,\sigma )\), however. In order to see this, consider the example in Fig. 15, where the edge \(vw_1\) with \(t(v)=t(w_1)=0\) cannot be contracted without violating the property that the resulting tree still explains the underlying co-RBMG.
To shed some light on the question how cotrees for a co-RBMG \((G,\sigma )\) and least resolved trees that explain \((G,\sigma )\) are related, we identify the edges of a cotree for \((G,\sigma )\) that can be contracted. To this end, we show that the sufficient conditions in Lemma 3 are also necessary for co-RBMGs.
Lemma 46
Let \((T,t,\sigma )\) be a not necessarily binary cotree explaining the co-RBMG \((G,\sigma )\) that is also a cotree for \((G,\sigma )\) and let \(e=uv\) be an inner edge of T. Then \((T_e,\sigma )\) explains \((G,\sigma )\) if and only if either Property (1) or (2) from Lemma 3 is satisfied.
Proof
By Lemma 3, Properties (1) and (2) ensure that \((T_e,\sigma )\) explains \((G,\sigma )\).
Conversely, suppose that \((T_e,\sigma )\) explains \((G,\sigma )\). Since \((G,\sigma )\) is a co-RBMG, it is an hc-cograph by Theorem 9 and thus, \((T,t,\sigma )\) is an hc-cotree for \((G,\sigma )\). Let \({\mathcal {G}}_x:=(G,\sigma )[L(T(x))]\) for \(x\in V(T)\). Clearly, \((T(u),t_{|L(T(u))},\sigma _{|L(T(u))})\) is an hc-cotree for \({\mathcal {G}}_u\) and thus, \({\mathcal {G}}_u\) is an hc-cograph. Hence, \({\mathcal {G}}_u\) can be written as \({\mathcal {G}}_v\star (H,\sigma _{H})\), where  and \((H,\sigma _{H}) = \star _{x\in C}{\mathcal {G}}_x\) for \(C:=\mathsf {child} _T(u){\setminus } \{v\}\). Clearly, either \(t(u)=1\) (in case \(\star = {{\,\mathrm{\triangledown }\,}}\)) or \(t(u)=0\) (in case
and \((H,\sigma _{H}) = \star _{x\in C}{\mathcal {G}}_x\) for \(C:=\mathsf {child} _T(u){\setminus } \{v\}\). Clearly, either \(t(u)=1\) (in case \(\star = {{\,\mathrm{\triangledown }\,}}\)) or \(t(u)=0\) (in case  ). As \((T(u),t_{|L(T(u))},\sigma _{|L(T(u))})\) is an hc-cotree, we have either \(\sigma (L(T(v'))) \cap \sigma (L(T(v))) = \emptyset \) for all \(v'\in \mathsf {child} _T(u)\) (in case \(\star = {{\,\mathrm{\triangledown }\,}}\)) or \(\sigma (L(T(v'))) \cap \sigma (L(T(v))) \in \{\sigma (L(T(v))),\sigma (L(T(v')))\}\) for all \(v'\in \mathsf {child} _T(u)\) (in case
). As \((T(u),t_{|L(T(u))},\sigma _{|L(T(u))})\) is an hc-cotree, we have either \(\sigma (L(T(v'))) \cap \sigma (L(T(v))) = \emptyset \) for all \(v'\in \mathsf {child} _T(u)\) (in case \(\star = {{\,\mathrm{\triangledown }\,}}\)) or \(\sigma (L(T(v'))) \cap \sigma (L(T(v))) \in \{\sigma (L(T(v))),\sigma (L(T(v')))\}\) for all \(v'\in \mathsf {child} _T(u)\) (in case  ).
).
Thus, if \(\star ={{\,\mathrm{\triangledown }\,}}\), then we immediately obtain Property (1). In the second case, where \({\mathcal {G}}_u={\mathcal {G}}_v\) \((H',\sigma _{H'})\), the color constraint (K3cc) implies \(\sigma (L(T(v)))\subseteq \sigma (L(T(v')))\) or \(\sigma (L(T(v')))\subsetneq \sigma (L(T(v)))\) for any \(v'\in \mathsf {child} _T(u)\). If the first case is true for all children of u in T, we obtain Property (2.i) of Lemma 3. Thus, suppose there exists some vertex \(v'\in \mathsf {child} _T(u)\) with \(\sigma (L(T(v')))\subsetneq \sigma (L(T(v)))\). Assume, for contradiction, that there is a vertex \(w\in \mathsf {child} _T(v)\) with \(S_{w,\lnot v'} \ne \emptyset \) and a color s such that s is contained in \(\sigma (L(T(v')))\) but not in \(\sigma (L(T(w)))\). Thus, in particular, there exists a vertex \(b\preceq _T v'\) with \(\sigma (b)=s\). Moreover, there is vertex \(a\preceq _T w\) with \(\sigma (a)=r\in S_{w,\lnot v'}\). Since \(r\notin \sigma (L(T(v')))\), the leaf a must be contained in the out-neighborhood of b in \(\vec {G}(T,\sigma )\). Since \(\sigma (L(T(v')))\subsetneq \sigma (L(T(v)))\) and \(s\notin \sigma (L(T(w)))\), there exists a vertex \(b'\in L(T(v)){\setminus } L(T(w))\) with \(\sigma (b')=s\). Hence, \({{\,\mathrm{lca}\,}}(a,b')=v\). Thus, b is not contained in the out-neighborhood of a, i.e., \(ab\notin E(G)\). However, if we contract \(e=uv\), we obtain the new vertex \(uv = {{\,\mathrm{lca}\,}}_{T_e}(a,b) \) in \(T_e\). Since \(r\notin \sigma (L(T(v')))\) and \(s\notin \sigma (L(T(w)))\), we immediately obtain \({{\,\mathrm{lca}\,}}_{T_e}(a,b) \preceq _{T_e} {{\,\mathrm{lca}\,}}_{T_e}(a,b')\) and \({{\,\mathrm{lca}\,}}_{T_e}(a,b) \preceq _{T_e} {{\,\mathrm{lca}\,}}_{T_e}(a',b)\) for all \(a'\) of color \(\sigma (a)\) and \(b'\) of color \(\sigma (b)\). Thus \(ab \in E(G(T_e,\sigma ))\) and hence, \((T_e,\sigma )\) does not explain \((G,\sigma )\); a contradiction.
\((H',\sigma _{H'})\), the color constraint (K3cc) implies \(\sigma (L(T(v)))\subseteq \sigma (L(T(v')))\) or \(\sigma (L(T(v')))\subsetneq \sigma (L(T(v)))\) for any \(v'\in \mathsf {child} _T(u)\). If the first case is true for all children of u in T, we obtain Property (2.i) of Lemma 3. Thus, suppose there exists some vertex \(v'\in \mathsf {child} _T(u)\) with \(\sigma (L(T(v')))\subsetneq \sigma (L(T(v)))\). Assume, for contradiction, that there is a vertex \(w\in \mathsf {child} _T(v)\) with \(S_{w,\lnot v'} \ne \emptyset \) and a color s such that s is contained in \(\sigma (L(T(v')))\) but not in \(\sigma (L(T(w)))\). Thus, in particular, there exists a vertex \(b\preceq _T v'\) with \(\sigma (b)=s\). Moreover, there is vertex \(a\preceq _T w\) with \(\sigma (a)=r\in S_{w,\lnot v'}\). Since \(r\notin \sigma (L(T(v')))\), the leaf a must be contained in the out-neighborhood of b in \(\vec {G}(T,\sigma )\). Since \(\sigma (L(T(v')))\subsetneq \sigma (L(T(v)))\) and \(s\notin \sigma (L(T(w)))\), there exists a vertex \(b'\in L(T(v)){\setminus } L(T(w))\) with \(\sigma (b')=s\). Hence, \({{\,\mathrm{lca}\,}}(a,b')=v\). Thus, b is not contained in the out-neighborhood of a, i.e., \(ab\notin E(G)\). However, if we contract \(e=uv\), we obtain the new vertex \(uv = {{\,\mathrm{lca}\,}}_{T_e}(a,b) \) in \(T_e\). Since \(r\notin \sigma (L(T(v')))\) and \(s\notin \sigma (L(T(w)))\), we immediately obtain \({{\,\mathrm{lca}\,}}_{T_e}(a,b) \preceq _{T_e} {{\,\mathrm{lca}\,}}_{T_e}(a,b')\) and \({{\,\mathrm{lca}\,}}_{T_e}(a,b) \preceq _{T_e} {{\,\mathrm{lca}\,}}_{T_e}(a',b)\) for all \(a'\) of color \(\sigma (a)\) and \(b'\) of color \(\sigma (b)\). Thus \(ab \in E(G(T_e,\sigma ))\) and hence, \((T_e,\sigma )\) does not explain \((G,\sigma )\); a contradiction.
\(\square \)
As an immediate consequence of Lemma 46(1) we obtain
Corollary 10
Let \((T,t,\sigma )\) be a not necessarily binary cotree explaining the co-RBMG \((G,\sigma )\) that is also a cotree for \((G,\sigma )\). If \(t(u)=1\) for an inner edge \(e=uv\) of T, then the tree \((T_e,\sigma )\) explains \((G,\sigma )\).
Now, Corollary 10 and Proposition 1 imply
Corollary 11
Let \((T,t,\sigma )\) be a not necessarily binary cotree explaining the co-RBMG \((G,\sigma )\) and let \(e=uv\) be an inner edge of T with \(t(u)=t(v)=1\). Then the tree \((T_e,t_e,\sigma )\) explains \((G,\sigma )\) and is a cotree for \((G,\sigma )\), where the vertex \(w=uv\) obtained by contracting the edge uv is labeled by \(t_e(w)=1\) and \(t_e(w')=t(w')\) for all other vertices \(w'\ne w\).
Thus, if \((T^G_{hc },t,\sigma )\) is a least resolved tree that explains \((G,\sigma )\), then it will not have any adjacent vertices labeled by 1. The situation is more complicated for 0-labeled vertices. Figure 15 shows that not all edges xy in \((T^G_{hc },t,\sigma )\) with \(t(x)=t(y)=0\) can be contracted. However, we obtain the following characterization, which is an immediate consequence of Proposition 1, Lemma 46 and Corollary 11.
Corollary 12
Let \((T,t,\sigma )\) be a not necessarily binary cotree explaining the co-RBMG \((G,\sigma )\) that is also a cotree for \((G,\sigma )\). Let \(e=uv\) be an inner edge of T. The following two statements are equivalent:
- 1.
\((T_e,t_e,\sigma )\) explains \((G,\sigma )\) and is a cotree for \((G,\sigma )\), where the vertex \(w=uv\) obtained by contracting the edge uv is labeled by \(t_e(w)=t(u)\) and \(t_e(w')=t(w')\) for all other vertices \(w'\ne w\),
- 2.
\(t(u)=t(v)\) and, if \(t(u)=0\), then e satisfies Properties (1) and (2) in Lemma 3.
If we apply Corollaries 11 and 12, then Proposition 1 implies that we always obtain a cotree \((T_e,t_e,\sigma )\) for \((G,\sigma )\). Hence, we can repeatedly apply Corollaries 11 and 12 and conclude that the least resolved tree \((T,t,\sigma )\) explaining \((G,\sigma )\) does neither contain edges xy with \(t(x)=t(y)=1\) nor edges xy with \(t(x)=t(y)=0\) satisfying Lemma 3(1) and (2). Moreover, Corollary 10 allows us to contract edges xy with \(t(x)=1\ne t(y)\). In this case, however, Proposition 1 implies that \((T_e,t')\) is not a cotree for the co-RBMG \((G,\sigma )\) for all possible labelings \(t':V^0\rightarrow \{0,1\}\). Hence, the question arises, how often we can apply Corollary 10. An answer is provided by the next result:
Lemma 47
Let \((T,t,\sigma )\) be a not necessarily binary cotree that explains the co-RBMG \((G,\sigma )\) and that is a cotree for \((G,\sigma )\). Let A be the set of all inner edges \(e=uv\) of T with \(t(u)=1\). Then, \((T_{B},\sigma )\) explains \((G,\sigma )\) for all \(B\subseteq A\).
Proof
Any edge \(e=uv \in B\) is contracted to some vertex \(u_e\) in \((T_{B},\sigma )\).
Let \(e=uv\in A\). By definition of A, we have \(t(u)=1\). Clearly, \((T(u),t_{|L(T(u))},\sigma _{|L(T(u))})\) is an hc-cotree. Hence, \(\sigma (L(T(v_1)))\cap \sigma (L(T(v_2)))=\emptyset \) for any two distinct vertices \(v_1,v_2\in \mathsf {child} _{T}(u)\). Now assume that we have contracted e to obtain \((T_e,\sigma )\). By Corollary 10, \((T_e,\sigma )\) explains \((G,\sigma )\). Moreover suppose that there exists another edge \(f = uv'\in A\) which corresponds to \(u_ev'\) in \((T_e,\sigma )\). In \((T,\sigma )\), we have \(\sigma (L(T(v)))\cap \sigma (L(T(v')))=\emptyset \) which, in particular, implies \(\sigma (L(T(v')))\cap \sigma (L(T(w)))=\emptyset \) for all \(w\in \mathsf {child} _T(v)\). In \((T_e,\sigma )\), the children of \(u_e\) are now \(\mathsf {child} _{T_e}(u_e) = (\mathsf {child} _T(u){\setminus } \{v\})\cup \mathsf {child} _T(v)\). Thus, \(\sigma (L(T(v')))\cap \sigma (L(T(v'')))=\emptyset \) for all \(v''\in \mathsf {child} _{T_e}(u_e)\). Lemma 3(1) implies that f can be contracted to obtain the tree \((T_{ef},\sigma )\) that explains \((G,\sigma )\). Repeated application of the latter arguments shows that all edges incident to vertex u in \((T,\sigma )\) can be contracted.
Finally, the contraction of the edges can be performed in a top-down fashion. In this case, the contraction of edges incident to u does not influence the children of any vertex \(u'\) that is incident to some edge \(e'= u'v'\) having label \(t(u')=1\). That is, we can apply the latter arguments to all edges in B independently, from which we conclude that \((T_{B},\sigma )\) explains \((G,\sigma )\) for all \(B\subseteq A\). \(\square \)
For the contraction of edges xy with \(t(x)=0\ne t(y)\), however, the situation becomes more complicated.
Lemma 48
Let \((T,t,\sigma )\) be a not necessarily binary cotree that explains the co-RBMG \((G,\sigma )\) and is a cotree for \((G,\sigma )\). Moreover, let \(u\in V^0(T)\) be an inner vertex with \(t(u)=0\) and \(A=\{e_1,\dots ,e_k\}\) be the set of all inner edges \(e_i=uv_i\in E(T)\) with \(v_i\in \mathsf {child} _T(u)\) such that \(t(v_i)=1\) and \(e_i\) is redundant in \((T,\sigma )\). Then, \((T_e,\sigma )\) explains \((G,\sigma )\) for all \(e\in A\) but \((T_{B},\sigma )\) does not explain \((G,\sigma )\) for all \(B\subseteq A\) with \(|B|\ge 2\).
Proof
Let the edges \(e=uv\) and \(f=uv'\) be contained in A. Since e and f are redundant, \((T_e,\sigma )\) and \((T_f,\sigma )\) both explain \((G,\sigma )\). It suffices to show that \((T_{ef},\sigma )\) does not explain \((G,\sigma )\). Following the same argumentation as in the beginning of the proof of Lemma 46, we conclude that \((T(v),t_{|L(T(v))},\sigma _{|L(T(v))})\) is an hc-cotree. This and \(t(v)=1\) implies \(\sigma (L(T(w_i)))\cap \sigma (L(T(w_j)))=\emptyset \) for any two distinct vertices \(w_i, w_j\in \mathsf {child} _T(v)\). Hence, \(\sigma (L(T(v)))\) is partitioned into the sets \(\sigma (L(T(w_1))), \dots , \sigma (L(T(w_k)))\) with \(w_i\in \mathsf {child} _T(v)\), \(1\le i \le k\). Analogously, \(\sigma (L(T(w'_1))),\dots , \sigma (L(T(w'_m)))\) with \(w'_i\in \mathsf {child} _T(v')\), \(1\le i \le m\) forms a partition of \(\sigma (L(T(v')))\). Consider an arbitrary but fixed vertex \(w\in \mathsf {child} _T(v)\). Assume, for contradiction, that \((T_{ef},\sigma )\) explains \((G,\sigma )\) and denote by \(u_{ef}\) the inner vertex in \(T_{ef}\) that is obtained by contracting the edges uv and \(uv'\). Since \((G,\sigma )\) is an hc-cograph and \(t(u)=0\), the color sets \(\sigma (L(T(v)))\) and \(\sigma (L(T(v')))\) are neither disjoint nor do they overlap. As \((T_{ef},\sigma )=(T_{fe},\sigma )\), we can w.l.o.g. assume that \(\sigma (L(T(v'))) \subseteq \sigma (L(T(v)))\).
Now, let \(w'\in \mathsf {child} _T(v')\) such that there is some \(z'\in L(T(w'))\) with \(\sigma (z')=t \notin \sigma (L(T(w)))\). Let \(x\in L(T(w))\) with \(\sigma (x)=r\). Since \(t(u)=0\) and \(u={{\,\mathrm{lca}\,}}_T(x,z')\), we have \(xz'\notin E(G)\). However, as \(\sigma (L(T(v')))\subseteq \sigma (L(T(v)))\), there is some child \({\widetilde{w}}\in \mathsf {child} _T(v)\) distinct from w such that \(t\in \sigma (L(T({\widetilde{w}})))\). Let \({\widetilde{z}}\in L(T({\widetilde{w}}))\) with \(\sigma ({\widetilde{z}})=t\). Since \(t(v)=1\), we have \(x{\widetilde{z}}\in E(G)\). As \((T_{ef},\sigma )\) explains \((G,\sigma )\), \(x{\widetilde{z}}\) must be an edge in \(G(T_{ef}, \sigma )\). Hence, \({{\,\mathrm{lca}\,}}_{T_{ef}}(x,{\widetilde{z}}) = u_{ef}\preceq _{T_{ef}} {{\,\mathrm{lca}\,}}_{T_{ef}}(x,z'')\) and \({{\,\mathrm{lca}\,}}_{T_{ef}}(x,{\widetilde{z}}) = u_{ef}\preceq _{T_{ef}} {{\,\mathrm{lca}\,}}_{T_{ef}}(x'',{\widetilde{z}})\) for all \(x''\in L[\sigma (x)]\) and \(z''\in L[t]\). However, by construction of \(T_{ef}\), we have \({{\,\mathrm{lca}\,}}_{T_{ef}}(x,z') = {{\,\mathrm{lca}\,}}_{T_{ef}}(x,{\widetilde{z}}) = u_{ef}\). Hence, if \(r\notin \sigma (L(T(w')))\), then \(x{\widetilde{z}} \in E(G(T_{ef},\sigma ))\) implies that \(x z'\) is an edge in \(G(T_{ef},\sigma )\); a contradiction to \(xz'\notin E(G)\). Now assume that \(r\in \sigma (L(T(w')))\). Clearly, \(v'\) must have at least one further child \(w''\) with \(s\in \sigma (L(T(w'')))\) and \(s\notin \sigma (L(T(w')))\). In particular, \(r,t\notin \sigma (L(T(w'')))\). Since \(\sigma (L(T(v'))) \subseteq \sigma (L(T(v)))\), there exists a leaf \(y \in L(T(v))\) with \(\sigma (y)=s\). Now, we either have \(y\preceq _T w\) or \(y\preceq _T {\widetilde{w}}\) or \(y\preceq _T {\hat{w}}\in \mathsf {child} _T(v){\setminus } \{w,{\widetilde{w}}\}\). In any case, \(t(v)=1\) implies that at least one of the edges xy or \(y{\widetilde{z}}\) must be contained in G. Assume \(xy\in E(G)\). Since \(t(u)=0\), we have \(xy''\notin E(G)\) for any \(y''\in L(T(w'')) \cap L[s]\). On the other hand, as \(r\notin \sigma (L(T(w'')))\), we can apply the preceding argumentation to infer from \(xy\in E(G(T_{ef},\sigma ))\) that \(x y''\) is an edge in \(G(T_{ef},\sigma )\); a contradiction. Analogously, the existence of an edge \(y{\widetilde{z}}\) in G yields a contradiction as well. Hence, \((T_{ef},\sigma )\) does not explain \((G,\sigma )\). \(\square \)
The previous results can finally be used to obtain a least resolved tree \((T,\sigma )\) from a cotree \((T',t,\sigma )\) for a given co-RBMG \((G,\sigma )\) that also explains \((G,\sigma )\). Instead of checking all inner edges of \(T'\) for redundancy, Lemma 47 can be applied to identify promptly many redundant edges, which considerably reduces the number of edges that need to be checked. This idea is implemented in Algorithm 2, which returns a least resolved tree that explains \((G,\sigma )\). Lemma 48, however, suggests that this least resolved tree is not necessarily unique for \((G,\sigma )\).

Theorem 12
Let \((G,\sigma )\) be a co-RBMG that is explained by \((T,t,\sigma )\) such that \((T,t,\sigma )\) is also a cotree for \((G,\sigma )\). Then, Algorithm 2 returns a least resolved tree that explains \((G,\sigma )\), in polynomial time.
Proof
Lemma 47 implies that all inner edges \(e=uv\) with \(t(u)=1\) can be contracted, which is done in Line 2–4. Afterwards, we check for all remaining inner edges \(e=uv\) whether they are redundant or not, and, if so, contract them. In summary, the algorithm is correct. Clearly, all steps including the check for redundancy as in Lemma 2 can be done in polynomial time. \(\square \)
Rights and permissions
About this article
Cite this article
Geiß, M., Stadler, P.F. & Hellmuth, M. Reciprocal best match graphs. J. Math. Biol. 80, 865–953 (2020). https://doi.org/10.1007/s00285-019-01444-2
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-019-01444-2
Keywords
- Pairwise best hit
- Reciprocal best match heuristics
- Vertex colored graph
- Phylogenetic tree
- Hierarchically colored cograph



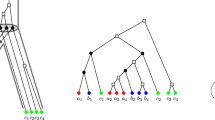
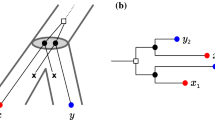





 and
and 