Gravitational Lensing from a Spacetime Perspective

Abstract

The theory of gravitational lensing is reviewed from a spacetime perspective, without quasi-Newtonian approximations. More precisely, the review covers all aspects of gravitational lensing where light propagation is described in terms of lightlike geodesics of a metric of Lorentzian signature. It includes the basic equations and the relevant techniques for calculating the position, the shape, and the brightness of images in an arbitrary general-relativistic spacetime. It also includes general theorems on the classification of caustics, on criteria for multiple imaging, and on the possible number of images. The general results are illustrated with examples of spacetimes where the lensing features can be explicitly calculated, including the Schwarzschild spacetime, the Kerr spacetime, the spacetime of a straight string, plane gravitational waves, and others.

1 Introduction

In its most general sense, gravitational lensing is a collective term for all effects of a gravitational field on the propagation of electromagnetic radiation, with the latter usually described in terms of rays. According to general relativity, the gravitational field is coded in a metric of Lorentzian signature on the 4-dimensional spacetime manifold, and the light rays are the lightlike geodesics of this spacetime metric. From a mathematical point of view, the theory of gravitational lensing is thus the theory of lightlike geodesics in a 4-dimensional manifold with a Lorentzian metric.

The first observation of a ‘gravitational lensing’ effect was made when the deflection of star light by our Sun was verified during a Solar eclipse in 1919. Today, the list of observed phenomena includes the following:

• Multiple quasars.

  The gravitational field of a galaxy (or a cluster of galaxies) bends the light from a distant quasar in such a way that the observer on Earth sees two or more images of the quasar.

• Rings.

  An extended light source, like a galaxy or a lobe of a galaxy, is distorted into a closed or almost closed ring by the gravitational field of an intervening galaxy. This phenomenon occurs in situations where the gravitational field is almost rotationally symmetric, with observer and light source close to the axis of symmetry. It is observed primarily, but not exclusively, in the radio range.

• Arcs.

  Distant galaxies are distorted into arcs by the gravitational field of an intervening cluster of galaxies. Here the situation is less symmetric than in the case of rings. The effect is observed in the optical range and may produce “giant luminous arcs”, typically of a characteristic blue color.

• Microlensing.

  When a light source passes behind a compact mass, the focusing effect on the light leads to a temporal change in brightness (energy flux). This microlensing effect is routinely observed since the early 1990s by monitoring a large number of stars in the bulge of our Galaxy, in the Magellanic Clouds and in the Andromeda galaxy. Microlensing has also been observed on quasars.

• Image distortion by weak lensing.

  In cases where the distortion effect on galaxies is too weak for producing rings or arcs, it can be verified with statistical methods. By evaluating the shape of a large number of background galaxies in the field of a galaxy cluster, one can determine the surface mass density of the cluster. By evaluating fields without a foreground cluster one gets information about the large-scale mass distribution.

Observational aspects of gravitational lensing and methods of how to use lensing as a tool in astrophysics are the subject of the Living Review by Wambsganss [343]. There the reader may also find some notes on the history of lensing.

The present review is meant as complementary to the review by Wambsganss. While all the theoretical methods reviewed in [343] rely on quasi-Newtonian approximations, the present review is devoted to the theory of gravitational lensing from a spaectime perspective, without such approximations. Here the terminology is as follows: “Lensing from a spacetime perspective” means that light propagation is described in terms of lightlike geodesics of a general-relativistic spacetime metric, without further approximations. (The term “non-perturbative lensing” is sometimes used in the same sense.) “Quasi-Newtonian approximation” means that the general-relativistic spacetime formalism is reduced by approximative assumptions to essentially Newtonian terms (Newtonian space, Newtonian time, Newtonian gravitational field). The quasi-Newtonian approximation formalism of lensing comes in several variants, and the relation to the exact formalism is not always evident because sometimes plausibility and ad-hoc assumptions are implicitly made. A common feature of all variants is that they are “weak-field approximations” in the sense that the spacetime metric is decomposed into a background (“spacetime without the lens”) and a small perturbation of this background (“gravitational field of the lens”). For the background one usually chooses either Minkowski spacetime (isolated lens) or a spatially flat Robertson-Walker spacetime (lens embedded in a cosmological model). The background then defines a Euclidean 3-space, similar to Newtonian space, and the gravitational field of the lens is similar to a Newtonian gravitational field on this Euclidean 3-space. Treating the lens as a small perturbation of the background means that the gravitational field of the lens is weak and causes only a small deviation of the light rays from the straight lines in Euclidean 3-space. In its most traditional version, the formalism assumes in addition that the lens is “thin”, and that the lens and the light sources are at rest in Euclidean 3-space, but there are also variants for “thick” and moving lenses. Also, modifications for a spatially curved Robertson-Walker background exist, but in all variants a non-trivial topological or causal structure of spacetime is (explicitly or implicitly) excluded. At the center of the quasi-Newtonian formalism is a “lens equation” or “lens map”, which relates the position of a “lensed image” to the position of the corresponding “unlensed image”. In the most traditional version one considers a thin lens at rest, modeled by a Newtonian gravitational potential given on a plane in Euclidean 3-space (“lens plane”). The light rays are taken to be straight lines in Euclidean 3-space except for a sharp bend at the lens plane. For a fixed observer and light sources distributed on a plane parallel to the lens plane (“source plane”), the lens map is then a map from the lens plane to the source plane. In this way, the geometric spacetime setting of general relativity is completely covered behind a curtain of approximations, and one is left simply with a map from a plane to a plane. Details of the quasi-Newtonian approximation formalism can be found not only in the above-mentioned Living Review [343], but also in the monographs of Schneider, Ehlers, and Falco [299] and Petters, Levine, and Wambsganss [275].

The quasi-Newtonian approximation formalism has proven very successful for using gravitational lensing as a tool in astrophysics. This is impressively demonstrated by the work reviewed in [343]. On the other hand, studying lensing from a spacetime perspective is of relevance under three aspects:

• Didactical.

  The theoretical foundations of lensing can be properly formulated only in terms of the full formalism of general relativity. Working out examples with strong curvature and with non-trivial causal or topological structure demonstrates that, in principle, lensing situations can be much more complicated than suggested by the quasi-Newtonian formalism.

• Methodological.

  General theorems on lensing (e.g., criteria for multiple imaging, characterizations of caustics, etc.) should be formulated within the exact spacetime setting of general relativity, if possible, to make sure that they are not just an artifact of approximative assumptions. For those results which do not hold in arbitrary spacetimes, one should try to find the precise conditions on the spacetime under which they are true.

• Practical.

  There are some situations of astrophysical interest to which the quasi-Newtonian formalism does not apply. For instance, near a black hole light rays are so strongly bent that, in principle, they can make arbitrarily many turns around the hole. Clearly, in this situation it is impossible to use the quasi-Newtonian formalism which would treat these light rays as small perturbations of straight lines.

The present review tries to elucidate all three aspects. More precisely, the following subjects will be covered:

• The basic equations and all relevant techniques that are needed for calculating the position, the shape, and the brightness of images in an arbitrary general-relativistic spacetime are reviewed. Part of this material is well-established since decades, like the Sachs equations for the optical scalars (Section 2.3), which are of crucial relevance for calculating distance measures (Section 2.4), image distortion (Section 2.5), and the brightness of images (Section 2.6). It is included here to keep the review self-contained. Other parts refer to more recent developments which are far from being fully explored, like the exact lens map (Section 2.1) and variational techniques (Section 2.9). Specifications and simplifications are possible for spacetimes with symmetries. The case of spherically symmetric and static spacetimes is treated in greater detail (Section 4.3).

• General theorems on lensing in arbitrary spacetimes, or in certain classes of spacetimes, are reviewed. Some of these results are of a local character, like the classification of locally stable caustics (Section 2.2). Others are related to global aspects, like the criteria for multiple imaging in terms of conjugate points and cut points (Sections 2.7 and 2.8). The global theorems can be considerably strengthened if one restricts to globally hyperbolic spacetimes (Section 3.1) or, more specifically, to asymptotically simple and empty spacetimes (Section 3.4). The latter may be viewed as spacetime models for isolated transparent lenses. Also, in globally hyperbolic spacetimes Morse theory can be used for investigating whether the total number of images is finite or infinite, even or odd (Section 3.3). In a spherically symmetric and static spacetime, the occurrence of an infinite sequence of images is related to the occurrence of a “light sphere” (circular lightlike geodesics), like in the Schwarzschild spacetime at r = 3m (Section 4.3).

• Several examples of spacetimes are considered, where the lightlike geodesics and, thus, the lensing features can be calculated explicitly. The examples are chosen such that they illustrate the general results. Therefore, in many parts of the review the reader will find suggestions to look at pictures in the example section. The best known and astrophysically most relevant examples are the Schwarzschild spacetime (Section 5.1), the Kerr spacetime (Section 5.8) and the spacetime of a straight string (Section 5.10). Schwarzschild black hole lensing and Kerr black hole lensing was intensively investigated already in the 1960s, 1970s, and 1980s, with astrophysical applications concentrating on observable features of accretion disks. More recently, the increasing evidence that there is a black hole at the center of our Galaxy (and probably at the center of most galaxies) has led to renewed and intensified interest in black hole lensing (see Sections 5.1 and 5.8). This is a major reason for the increasing number of articles on lensing beyond the quasi-Newtonian approximation. (It is, of course, true that this number is still small in comparison to the huge number of all articles on lensing; see [298, 244] for extensive lensing bibliographies.)

This introduction ends with some notes on subjects not covered in this review:

• Wave optics.

  In the electromagnetic theory, light is described by wavelike solutions to Maxwell’s equations. The ray-optical treatment used throughout this review is the standard high-frequency approximation (geometric optics approximation) of the electromagnetic theory for light propagation in vacuum on a general-relativistic spacetime (see, e.g., [225], § 22.5 or [299], Section 3.2). (Other notions of vacuum light rays, based on a different approximation procedure, have been occasionally suggested [217], but will not be considered here. Also, results specific to spacetime dimensions other than four or to gravitational theories other than Einstein’s are not covered.) For most applications to lensing the ray-optical treatment is valid and appropriate. An exception, where wave-optical corrections are necessary, is the calculation of the brightness of images if a light source comes very close to the caustic of the observer’s light cone (see Section 2.6).

• Light propagation in matter.

  If light is directly influenced by a medium, the light rays are no longer the lightlike geodesics of the spacetime metric. For an isotropic non-dispersive medium, they are the lightlike geodesics of another metric which is again of Lorentzian signature. (This “optical metric” was introduced by Gordon [143]. For a rigourous derivation, starting from Maxwell’s equation in an isotropic non-dispersive medium, see Ehlers [88].) Hence, the formalism used throughout this review still applies to this situation after an appropriate re-interpretation of the metric. In anisotropic or dispersive media, however, the light rays are not the lightlike geodesics of a Lorentzian metric. There are some lensing situations where the influence of matter has to be taken into account. For instance., for the deflection of radio signals by our Sun the influence of the plasma in the Solar corona (to be treated as a dispersive medium) is very well measurable. However, such situations will not be considered in this review. For light propagation in media on a general-relativistic spacetime, see [269] and references cited therein.

• Kinetic theory.

  As an alternative to the (geometric optics approximation of) electromagnetic theory, light can be treated as a photon gas, using the formalism of kinetic theory. This has relevance, e.g., for the cosmic background radiation. For basic notions of general-relativistic kinetic theory see, e.g., [89]. Apart from some occasional remarks, kinetic theory will not be considered in this review.

• Derivation of the quasi-Newtonian formalism.

  It is not satisfacory if the quasi-Newtonian formalism of lensing is set up with the help of ad-hoc assumptions, even if the latter look plausible. From a methodological point of view, it is more desirable to start from the exact spacetime setting of general relativity and to derive the quasi-Newtonian lens equation by a well-defined approximation procedure. In comparison to earlier such derivations [299, 294, 303] more recent effort has led to considerable improvements. For lenses embedded in a cosmological model, see Pyne and Birkinshaw [283] who consider lenses that need not be thin and may be moving on a Robertson-Walker background (with positive, negative, or zero spatial curvature). For the non-cosmological situation, a Lorentz covariant approximation formalism was derived by Kopeikin and Schäfer [185]. Here Minkowski spacetime is taken as the background, and again the lenses need not be thin and may be moving.

2 Lensing in Arbitrary Spacetimes

By a spacetime we mean a 4-dimensional manifold ${\mathcal M}$ with a (C^∞, if not otherwise stated) metric tensor field g of signature (+, +, +, −) that is time-oriented. The latter means that the non-spacelike vectors make up two connected components in the entire tangent bundle, one of which is called “future-pointing” and the other one “past-pointing”. Throughout this review we restrict to the case that the light rays are freely propagating in vacuum, i.e., are not influenced by mirrors, refractive media, or any other impediments. The light rays are then the lightlike geodesics of the spacetime metric. We first summarize results on the lightlike geodesics that hold in arbitrary spacetimes. In Section 3 these results will be specified for spacetimes with conditions on the causal structure and in Section 4 for spacetimes with symmetries.

2.1 Light cone and exact lens map

In an arbitrary spacetime (${\mathcal M}$, g), what an observer at an event p_O can see is determined by the lightlike geodesics that issue from p_O into the past. Their union gives the past light cone of p_O. This is the central geometric object for lensing from the spacetime perspective. For a point source with worldline γ_S, each past-oriented lightlike geodesic λ from p_O to γ_S gives rise to an image of γ_S on the observer’s sky. One should view any such λ as the central ray of a thin bundle that is focused by the observer’s eye lens onto the observer’s retina (or by a telescope onto a photographic plate). Hence, the intersection of the past light cone with the world-line of a point source (or with the world-tube of an extended source) determines the visual appearance of the latter on the observer’s sky.

In mathematical terms, the observer’s sky or celestial sphere $({{\mathcal S}_{\rm{O}}})$ can be viewed as the set of all lightlike directions at p_O. Every such direction defines a unique (up to parametrization) lightlike geodesic through p_O, so $({{\mathcal S}_{\rm{O}}})$ may also be viewed as a subset of the space of all lightlike geodesics in (${\mathcal M},g$) (cf. [209]). One may choose at p_O a future-pointing vector U_O with g(U_O, U_O) = −1, to be interpreted as the 4-velocity of the observer. This allows identifying the observer’s sky ${{\mathcal S}_{\rm{O}}}$ with a subset of the tangent space ${T_{P{\rm{O}}}}{\mathcal M}$,

$${{\mathcal S}_{\rm{O}}} \simeq \{w \in {T_{p{\rm{O}}}}{\mathcal M}\vert g(w,w) = 0\,\,{\rm{and}}\,\,g(w,{U_{\rm{O}}}) = 1\}.$$

(1)

If U_O is changed, this representation changes according to the standard aberration formula of special relativity. By definition of the exponential map exp, every affinely parametrized geodesic s ↦ τ(s) satisfies $\lambda (s) = \exp (s\dot \lambda (0))$. Thus, the past light cone of p_O is the image of the map

$$(s,w) \mapsto \exp (sw),$$

(2)

which is defined on a subset of $]0,\infty [ \times {{\mathcal S}_{\rm{O}}}$. If we restrict to values of s sufficiently close to 0, the map (2) is an embedding, i.e., this truncated light cone is an embedded submanifold; this follows from the well-known fact that exp maps a neighborhood of the origin, in each tangent space, diffeomorphically into the manifold. However, if we extend the map (2) to larger values of s, it is in general neither injective nor an immersion; it may form folds, cusps, and other forms of caustics, or transverse self-intersections. This observation is of crucial importance in view of lensing. There are some lensing phenomena, such as multiple imaging and image distortion of (point) sources into (1-dimensional) rings, which can occur only if the light cone fails to be an embedded submanifold (see Section 2.8). Such lensing phenomena are summarized under the name strong lensing effects. As long as the light cone is an embedded submanifold, the effects exerted by the gravitational field on the apparent shape and on the apparent brightness of light sources are called weak lensing effects. For examples of light cones with caustics and/or transverse self-intersections, see Figures 12, 24, and 25. These pictures show light cones in spacetimes with symmetries, so their structure is rather regular. A realistic model of our own light cone, in the real world, would have to take into account numerous irregularly distributed inhomogeneities (“clumps”) that bend light rays in their neighborhood. Ellis, Bassett, and Dunsby [99] estimate that such a light cone would have at least 10²² caustics which are hierarchically structured in a way that reminds of fractals.

For calculations it is recommendable to introduce coordinates on the observer’s past light cone. This can be done by choosing an orthonormal tetrad (e₀, e₁, e₂, e₃) with e₀ = −U_O at the observation event p_O. This parametrizes the points of the observer’s celestial sphere by spherical coordinates (Ψ, Θ),

$$w = \sin \Theta \cos \Psi \,{e_1} + \sin \Theta \sin \Psi \,{e_2} + \cos \Theta \,{e_3} + {e_0}.$$

(3)

In this representation, map (2) maps each (s, Ψ Θ) to a spacetime point. Letting the observation event float along the observer’s worldline, parametrized by proper time τ, gives a map that assigns to each (s, Ψ, Θ, τ) a spacetime point. In terms of coordinates x = (x⁰, x¹, x², x³) on the spacetime manifold, this map is of the form

$${x^i} = {F^i}(s,\Psi ,\Theta ,\tau),\quad \quad i = 0,1,2,3.$$

(4)

It can be viewed as a map from the world as it appears to the observer (via optical observations) to the world as it is. The observational coordinates (s, Ψ, Θ, τ) were introduced by Ellis [98] (see [100] for a detailed discussion). They are particularly useful in cosmology but can be introduced for any observer in any spacetime. It is useful to consider observables, such as distance measures (see Section 2.4) or the ellipticity that describes image distortion (see Section 2.5) as functions of the observational coordinates. Some observables, e.g., the redshift and the luminosity distance, are not determined by the spacetime geometry and the observer alone, but also depend on the 4-velocities of the light sources. If a vector field U with g(U, U) = −1 has been fixed, one may restrict to an observer and to light sources which are integral curves of U. The above-mentioned observables, like redshift and luminosity distance, are then uniquely determined as functions of the observational coordinates. In applications to cosmology one chooses U as tracing the mean flow of luminous matter (“Hubble flow”) or as the rest system of the cosmic background radiation; present observations are compatible with the assumption that these two distinguished observer fields coincide [32].

Writing map (4) explicitly requires solving the lightlike geodesic equation. This is usually done, using standard index notation, in the Lagrangian formalism, with the Lagrangian ${\mathcal L} = {1 \over 2}{g_{ij}}(x){{\dot x}^i}{{\dot x}^j}$, or in the Hamiltonian formalism, with the Hamiltonian ${\mathcal H} = {1 \over 2}{g^{ij}}(x){p_i}{p_j}$. A non-trivial example where the solutions can be explicitly written in terms of elementary functions is the string spacetime of Section 5.10. Somewhat more general, although still very special, is the situation that the lightlike geodesic equation admits three independent constants of motion in addition to the obvious one g^ij(x)p_ip_j = 0. If, for any pair of the four constants of motion, the Poisson bracket vanishes (“complete integrability”), the lightlike geodesic equation can be reduced to first-order form, i.e., the light cone can be written in terms of integrals over the metric coefficients. This is true, e.g., in spherically symmetric and static spacetimes (see Section 4.3).

Having parametrized the past light cone of the observation event p_O in terms of (s, w), or more specifically in terms of (s, Ψ, Θ), one may set up an exact lens map. This exact lens map is analogous to the lens map of the quasi-Newtonian approximation formalism, as far as possible, but it is valid in an arbitrary spacetime without approximation. In the quasi-Newtonian formalism for thin lenses at rest, the lens map assigns to each point in the lens plane a point in the source plane (see, e.g., [299, 275, 343]). When working in an arbitrary spacetime without approximations, the observer’s sky ${{\mathcal S}_{\rm{O}}}$ is an obvious substitute for the lens plane. As a substitute for the source plane we choose a 3-dimensional submanifold ${\mathcal T}$ with a prescribed ruling by timelike curves. We assume that ${\mathcal T}$ is globally of the form ${\mathcal Q} \times {\mathbb R}$, where the points of the 2-manifold ${\mathcal Q}$ label the timelike curves by which ${\mathcal T}$ is ruled. These timelike curves are to be interpreted as the worldlines of light sources. We call any such ${\mathcal T}$ a source surface. In a nutshell, choosing a source surface means choosing a two-parameter family of light sources.

The exact lens map is a map from ${{\mathcal S}_{\rm{O}}}$ to ${\mathcal Q}$. It is defined by following, for each $w \in {{\mathcal S}_{\rm{O}}}$, the past-pointing geodesic with initial vector ω until it meets ${\mathcal T}$ and then projecting to ${\mathcal Q}$ (see Figure 1). In other words, the exact lens map says, for each point on the observer’s celestial sphere, which of the chosen light sources is seen at this point. Clearly, non-invertibility of the lens map indicates multiple imaging. What one chooses for ${\mathcal T}$ depends on the situation. In applications to cosmology, one may choose galaxies at a fixed redshift z = z_S around the observer. In a spherically-symmetric and static spacetime one may choose static light sources at a fixed radius value r = r_S. Also, the surface of an extended light source is a possible choice for ${\mathcal T}$.

Figure 1

Illustration of the exact lens map. p_O is the chosen observation event, ${\mathcal T}$ is the chosen source surface. ${\mathcal T}$ is a hypersurface ruled by timelike curves (worldlines of light sources) which are labeled by the points of a 2-dimensional manifold ${\mathcal Q}$. The lens map is defined on the observer’s celestial sphere ${{\mathcal S}_{\rm{O}}}$, given by Equation (1) , and takes values in ${\mathcal Q}$. For each $w \in {{\mathcal S}_{\rm{O}}}$, one follows the lightlike geodesic with this initial direction until it meets ${\mathcal T}$ and then projects to ${\mathcal Q}$. For illustrating the exact lens map, it is an instructive exercise to intersect the light cones of Figures 12 , 24 , 25 , and 29 with various source surfaces ${\mathcal T}$.

The exact lens map was introduced by Frittelli and Newman [123] and further discussed in [91, 90]. The following global aspects of the exact lens map were investigated in [270]. First, in general the lens map is not defined on all of ${{\mathcal S}_{\rm{O}}}$ because not all past-oriented lightlike geodesics that start at p_O necessarily meet ${\mathcal T}$. Second, in general the lens map is multi-valued because a lightlike geodesic might meet ${\mathcal T}$ several times. Third, the lens map need not be differentiable and not even continuous because a lightlike geodesic might meet ${\mathcal T}$ tangentially. In [270], the notion of a simple lensing neighborhood is introduced which translates the statement that a deflector is transparent into precise mathematical language. It is shown that the lens map is globally well-defined and differentiable if the source surface is the boundary of such a simple lensing neighborhood, and that for each light source that does not meet the caustic of the observer’s past light cone the number of images is finite and odd. This result applies, as a special case, to asymptotically simple and empty spacetimes (see Section 3.4).

For expressing the exact lens map in coordinate language, it is recommendable to choose coordinates (x⁰, x¹, x², x³) such that the source surface ${\mathcal T}$ is given by the equation ${x^3} = x_{\rm{S}}^3$, with a constant $x_{\rm{S}}^3$, and that the worldlines of the light sources are x⁰-lines. In this situation the remaining coordinates x¹ and x² label the light sources and the exact lens map takes the form

$$(\Psi, \Theta) \mapsto ({x^1},{x^2}).$$

(5)

It is given by eliminating the two variables s and x⁰ from the four equations (4) with ${F^3}(s,\Psi, \Theta, \tau) = x_{\rm{S}}^3$ and fixed τ. This is the way in which the lens map was written in the original paper by Frittelli and Newman; see Equation (6) in [123]. (They used complex coordinates ($\eta, \bar \eta$) for the observer’s celestial sphere that are related to our spherical coordinates (Ψ, Θ) by stereographic projection.) In this explicit coordinate version, the exact lens map can be succesfully applied, in particular, to spherically symmetric and static spacetimes, with x⁰ = t, x¹ = ϕ, x² = ϑ, and x³ = r (see Section 4.3 and the Schwarzschild example in Section 5.1). The exact lens map can also be used for testing the reliability of approximation techniques. In [184] the authors find that the standard quasi-Newtonian approximation formalism may lead to significant errors for lensing configurations with two lenses.

2.2 Wave fronts

Wave fronts are related to light rays as solutions of the Hamilton-Jacobi equation are related to solutions of Hamilton’s equations in classical mechanics. For the case at hand (i.e., vacuum light propagation in an arbitrary spacetime, corresponding to the Hamiltonian ${\mathcal H} = {1 \over 2}{g^{ij}}(x){p_i}{p_j})$, a wave front is a subset of the spacetime that can be constructed in the following way:

• 1. Choose a spacelike 2-surface S that is orientable.

• 2. At each point of ${\mathcal S}$, choose a lightlike direction orthogonal to ${\mathcal S}$ that depends smoothly on the foot-point. (You have to choose between two possibilities.)

• 3. Take all lightlike geodesics that are tangent to the chosen directions. These lightlike geodesics are called the generators of the wave front, and the wave front is the union of all generators.

Clearly, a light cone is a special case of a wave front. One gets this special case by choosing for ${\mathcal S}$ an appropriate (small) sphere. Any wave front is the envelope of all light cones with vertices on the wave front. In this sense, general-relativistic wave fronts can be constructed according to the Huygens principle.

In the context of general relativity the notion of wave fronts was introduced by Kermack, McCrea, and Whittaker [180]. For a modern review article see, e.g., Ehlers and Newman [93].

A coordinate representation for a wave front can be given with the help of (local) coordinates (u¹, u¹) on ${\mathcal S}$. One chooses a parameter value s₀ and parametrizes each generator λ affinely such that $\lambda ({s_0}) \in {\mathcal S}$ and $\dot \lambda ({s_0})$ depends smoothly on the foot-point in ${\mathcal S}$. This gives the wave front as the image of a map

$$(s,{u^1},{u^2}) \mapsto {F^i}(s,{u^1},{u^2}),\quad \quad i = 0,1,2,3.$$

(6)

For light cones we may choose spherical coordinates, (u¹ = Ψ, u² = Θ), (cf. Equation (4) with fixed τ). Near s = s₀, map (6) is an embedding, i.e., the wave front is a submanifold. Orthogonality to ${\mathcal S}$ of the initial vectors $\dot \lambda ({s_0})$ assures that this submanifold is lightlike. Farther away from ${\mathcal S}$, however, the wave front need not be a submanifold. The caustic of the wave front is the set of all points where the map (6) is not an immersion, i.e., where its differential has rank < 3. As the derivative with respect to s is always non-zero, the rank can be 3 − 1 (caustic point of multiplicity one, astigmatic focusing) or 3 − 2 (caustic point of multiplicity two, anastigmatic focusing). In the first case, the cross-section of an “infinitesimally thin” bundle of generators collapses to a line, in the second case to a point (see Section 2.3). For the case that the wave front is a light cone with vertex p_O, caustic points are said to be conjugate to p_O along the respective generator. For an arbitrary wave front, one says that a caustic point is conjugate to any spacelike 2-surface in the wave front. In this sense, the terms “conjugate point” and “caustic point” are synonymous. Along each generator, caustic points are isolated (see Section 2.3) and thus denumerable. Hence, one may speak of the first caustic, the second caustic, and so on. At all points where the caustic is a manifold, it is either spacelike or lightlike. For instance, the caustic of the Schwarzschild light cone in Figure 12 is a spacelike curve; in the spacetime of a transparent string, the caustic of the light cone consists of two lightlike 2-manifolds that meet in a spacelike curve (see Figure 25).

Near a non-caustic point, a wave front is a hypersurface S = constant where S satisfies the Hamilton-Jacobi equation

$${g^{ij}}(x){\partial _i}S(x){\partial _j}S(x) = 0.$$

(7)

In the terminology of optics, Equation (7) is called the eikonal equation.

At caustic points, a wave front typically forms cuspidal edges or vertices whose geometry might be arbitrarily complicated, even locally. If one restricts to caustics which are stable against perturbations in a certain sense, then a local classification of caustics is possible with the help of Arnold’s singularity theory of Lagrangian or Legendrian maps. Full details of this theory can be found in [11]. For a readable review of Arnold’s results and its applications to wave fronts in general relativity, we refer again to [93]. In order to apply Arnold’s theory to wave fronts, one associates each wave front with a Legendrian submanifold in the projective cotangent bundle over ${\mathcal M}$ (or with a Lagrangian submanifold in an appropriately reduced bundle). A caustic point of the wave front corresponds to a point where the differential of the projection from the Legendrian submanifold to ${\mathcal M}$ has non-maximal rank. For the case $\dim ({\mathcal M}) = 4$, which is of interest here, Arnold has shown that there are only five types of caustic points that are stable with respect to perturbations within the class of all Legendrian submanifolds. They are known as fold, cusp, swallow-tail, pyramid, and purse (see Figure 2). Any other type of caustic is unstable in the sense that it changes non-diffeomorphically if it is perturbed within the class of Legendrian submanifolds.

Figure 2

Wave fronts that are locally stable in the sense of Arnold. Each picture shows the projection into 3-space of a wave-front, locally near a caustic point. The projection is made along the integral curves of a timelike vector field. The qualitative features are independent of which timelike vector field is chosen. In addition to regular, i.e., non-caustic, points (A₁), there are five kinds of stable points, known as fold (A₂), cusp (A₃), swallow-tail (A₄), pyramid ($D_4^ -$), and purse ($D_4^ +$). The A_k and D_k notation refers to a relation to exceptional groups (see [11]). The picture is taken from [150].

Fold singularities of a wave front form a lightlike 2-manifold in spacetime, on a sufficiently small neighborhood of any fold caustic point. The second picture in Figure 2 shows such a “fold surface”, projected to 3-space along the integral curves of a timelike vector field. This projected fold surface separates a region covered twice by the wave front from a region not covered at all. If the wave front is the past light cone of an observation event, and if one restricts to light sources with worldlines in a sufficiently small neighborhood of a fold caustic point, there are two images for light sources on one side and no images for light sources on the other side of the fold surface. Cusp singularities of a wave front form a spacelike curve in spacetime, again locally near any cusp caustic point. Such a curve is often called a “cusp ridge”. Along a cusp ridge, two fold surfaces meet tangentially. The third picture in Figure 2 shows the situation projected to 3-space. Near a cusp singularity of a past light cone, there is local triple-imaging for light sources in the wedge between the two fold surfaces and local single-imaging for light sources outside this wedge. Swallow-tail, pyramid, and purse singularities are points where two or more cusp ridges meet with a common tangent, as illustrated by the last three pictures in Figure 2.

Friedrich and Stewart [118] have demonstrated that all caustic types that are stable in the sense of Arnold can be realized by wave fronts in Minkowski spacetime. Moreover, they stated without proof that, quite generally, one gets the same stable caustic types if one allows for perturbations only within the class of wave fronts (rather than within the larger class of Legendrian submanifolds). A proof of this statement was claimed to be given in [150] where the Lagrangian rather than the Legendrian formalism was used. However, the main result of this paper (Theorem 4.4 of [150]) is actually too weak to justify this claim. A different version of the desired stability result was indeed proven by another approach. In this approach one concentrates on an instantaneous wave front, i.e., on the intersection of a wave front with a spacelike hypersurface ${\mathcal C}$. As an alternative terminology, one calls the intersection of a (“big”) wave front with a hypersurface ${\mathcal C}$ that is transverse to all generators a “small wave front”. Instantaneous wave fronts are special cases of small wave fronts. The caustic of a small wave front is the set of all points where the small wave front fails to be an immersed 2-dimensional submanifold of ${\mathcal C}$. If the spacetime is foliated by spacelike hypersurfaces, the caustic of a wave front is the union of the caustics of its small (= instantaneous) wave fronts. Such a foliation can always be achieved locally, and in several spacetimes of interest even globally. If one identifies different slices with the help of a timelike vector field, one can visualize a wave front, and in particular a light cone, as a motion of small (= instantaneous) wave fronts in 3-space. Examples are shown in Figures 13, 18, 19, 27, and 28. Mathematically, the same can be done for non-spacelike slices as long as they are transverse to the generators of the considered wave front (see Figure 30 for an example). Turning from (big) wave fronts to small wave fronts reduces the dimension by one. The only caustic points of a small wave front that are stable in the sense of Arnold are cusps and swallow-tails. What one wants to prove is that all other caustic points are unstable with respect to perturbations of the wave front within the class of wave fronts, keeping the metric and the slicing fixed. For spacelike slicings (i.e., for instantaneous wave fronts), this was indeed demonstrated by Low [210]. In this article, the author views wave fronts as subsets of the space ${\mathcal N}$ of all lightlike geodesics in (${\mathcal M},g$). General properties of this space ${\mathcal N}$ are derived in earlier articles by Low [208, 209] (also see Penrose and Rindler [262], volume II, where the space ${\mathcal N}$ is treated in twistor language). Low considers, in particular, the case of a globally hyperbolic spacetime [210]; he demonstrates the desired stability result for the intersections of a (big) wave front with Cauchy hypersurfaces (see Section 3.2). As every point in an arbitrary spacetime admits a globally hyperbolic neighborhood, this local stability result is universal. Figure 28 shows an instantaneous wave front with cusps and a swallow-tail point. Figure 13 shows instantaneous wave fronts with caustic points that are neither cusps nor swallow-tails; hence, they must be unstable with respect to perturbations of the wave front within the class of wave fronts.

It is to be emphasized that Low’s work allows to classify the stable caustics of small wave fronts, but not directly of (big) wave fronts. Clearly, a (big) wave front is a one-parameter family of small wave fronts. A qualitative change of a small wave front, in dependence of a parameter, is called a “metamorphosis” in the English literature and a “perestroika” in the Russian literature. Combining Low’s results with the theory of metamorphoses, or perestroikas, could lead to a classsification of the stable caustics of (big) wave fronts. However, this has not been worked out until now.

Wave fronts in general relativity have been studied in a long series of articles by Newman, Frittelli, and collaborators. For some aspects of their work see Sections 2.9 and 3.4. In the quasi-Newtonian approximation formalism of lensing, the classification of caustics is treated in great detail in the book by Petters, Levine, and Wambsganss [275]. Interesting related mateial can also be found in Blandford and Narayan [33]. For a nice exposition of caustics in ordinary optics see Berry and Upstill [28].

A light source that comes close to the caustic of the observer’s past light cone is seen strongly magnified. For a point source whose worldline passes exactly through the caustic, the ray-optical treatment even gives an infinite brightness (see Section 2.6). If a light source passes behind a compact deflecting mass, its brightness increases and decreases in the course of time, with a maximum at the moment of closest approach to the caustic. Such microlensing events are routinely observed by monitoring a large number of stars in the bulge of our Galaxy, in the Magellanic Clouds, and in the Andromeda Galaxy (see, e.g., [226] for an overview). In his millennium essay on future perspectives of gravitational lensing, Blandford [34] mentioned the possibility of observing a chosen light source strongly magnified over a period of time with the help of a space-born telescope. The idea is to guide the spacecraft such that the worldline of the light source remains in (or close to) the one-parameter family of caustics of past light cones of the spacecraft over a period of time. This futuristic idea of “caustic surfing” was mathematically further discussed by Frittelli and Petters [128].

2.3 Optical scalars and Sachs equations

For the calculation of distance measures, of image distortion, and of the brightness of images one has to study the Jacobi equation (= equation of geodesic deviation) along lightlike geodesics. This is usually done in terms of the optical scalars which were introduced by Sachs et al. [172, 292]. Related background material on lightlike geodesic congruences can be found in many text-books (see, e.g., Wald [341], Section 9.2). In view of applications to lensing, a particularly useful exposition was given by Seitz, Schneider and Ehlers [303]. In the following the basic notions and results will be summarized.

2.3.1 Infinitesimally thin bundles

Let s ↦ λ(s) be an affinely parametrized lightlike geodesic with tangent vector field $K = \dot \lambda$. We assume that λ is past-oriented, because in applications to lensing one usually considers rays from the observer to the source. We use the summation convention for capital indices A, B, … taking the values 1 and 2. An infinitesimally thin bundle (with elliptical cross-section) along λ is a set

$${\mathcal B} = \{{c^A}{Y_A}\vert {c^1},{c^2} \in \mathbb{R},\,\quad {\delta _{AB}}{c^A}{c^B} \leq 1\}.$$

(8)

Here δ_ab denotes the Kronecker delta, and Y₁ and Y₂ are two vector fields along λ with

$${\nabla _K}{\nabla _K}{Y_A} = R(K,{Y_A},K),$$

(9)

$$g(K,{Y_A}) = 0,$$

(10)

such that Y₁(s), Y₂(s), and K(s) are linearly independent for almost all s. As usual, R denotes the curvature tensor, defined by

$$R(X,Y,Z) = {\nabla _X}{\nabla _Y}Z - {\nabla _Y}{\nabla _X}Z - {\nabla _{[X,Y]}}Z.$$

(11)

Equation (9) is the Jacobi equation. It is a precise mathematical formulation of the statement that “the arrow-head of Y_a traces an infinitesimally neighboring geodesic”. Equation (10) guarantees that this neighboring geodesic is, again, lightlike and spatially related to λ.

2.3.2 Sachs basis

For discussing the geometry of infinitesimally thin bundles it is usual to introduce a Sachs basis, i.e., two vector fields E₁ and E₂ along λ that are orthonormal, orthogonal to $K = \dot \lambda$, and parallelly transported,

$$g({E_A},{E_B}) = {\delta _{AB}},\quad g(K,{E_A}) = 0,\quad {\nabla _K}{E_A} = 0.$$

(12)

Apart from the possibility to interchange them, E₁ and E₂ are unique up to transformations

$${\tilde E_1} = \cos \alpha {E_1} + \sin \alpha {E_2} + {a_1}K,$$

(13)

$${\tilde E_2} = - \sin \alpha {E_1} + \cos \alpha {E_2} + {a_2}K,$$

(14)

where a, a₁, and a₂ are constant along λ. A Sachs basis determines a unique vector field U with g(U, U) = −1 and g(U, K) = 1 along λ that is perpendicular to E₁, and E₂. As K is assumed past-oriented, U is future-oriented. In the rest system of the observer field U, the Sachs basis spans the 2-space perpendicular to the ray. It is helpful to interpret this 2-space as a “screen”; correspondingly, linear combinations of E₁ and E₂ are often refered to as “screen vectors”.

2.3.3 Jacobi matrix

With respect to a Sachs basis, the basis vector fields Y₁ and Y₂ of an infinitesimally thin bundle can be represented as

$${Y_A} = D_A^B{E_B} + {y_A}K.$$

(15)

The Jacobi matrix $D = (D_A^B)$ relates the shape of the cross-section of the infinitesimally thin bundle to the Sachs basis (see Figure 3). Equation (9) implies that D satisfies the matrix Jacobi equation

$$\ddot D = DR,$$

(16)

where an overdot means derivative with respect to the affine parameter s, and

$$R = \left({\begin{array}{*{20}c} {{\Phi _{00}}} & 0 \\ 0 & {{\Phi _{00}}} \\ \end{array}} \right) + \left({\begin{array}{*{20}c}{- {{\rm Re}} ({\psi _0})} & {{{\rm Im}} ({\psi _0})} \\ {{{\rm Im}} ({\psi _0})} & {{{\rm Re}} ({\psi _0})} \\ \end{array}} \right)$$

(17)

is the optical tidal matrix, with

$${\Phi _{00}} = - {1 \over 2}{\rm{Ric}}(K,K),\quad {\psi _0} = - {1 \over 2}C({E_1} - i{E_2},K,{E_1} - i{E_2},K).$$

(18)

Here Ric denotes the Ricci tensor, defined by Ric(X, Y) = tr(R(·, X, Y)), and C denotes the conformal curvature tensor (= Weyl tensor). The notation in Equation (18) is chosen in agreement with the Newman-Penrose formalism (cf., e.g., [54]). As Y₁, Y₂, and K are not everywhere linearly dependent, det(D) does not vanish identically. Linearity of the matrix Jacobi equation implies that det(D) has only isolated zeros. These are the “caustic points” of the bundle (see below).

Figure 3

Cross-section of an infinitesimally thin bundle. The Jacobi matrix (19) relates the Jacobi fields Y₁ and Y₂ that span the bundle to the Sachs basis vectors E₁ and E₂. The shape parameters D₊, D₋, and χ determine the outline of the cross-section; the angle ψ that appears in Equation (19) does not show in the outline. The picture shows the projection into the 2-space (“screen”) spanned by E₁ and E₂; note that, in general, Y₁ and Y₂ have components perpendicular to the screen.

2.3.4 Shape parameters

The Jacobi matrix D can be parametrized according to

$$D = \left({\begin{array}{*{20}c}{\cos \psi} & {- \sin \psi} \\ {\sin \psi} & {\cos \psi} \\ \end{array}} \right)\, \, \left({\begin{array}{*{20}c}{{D_ +}} & 0 \\ 0 & {D_-} \\ \end{array}} \right)\, \, \left({\begin{array}{*{20}c}{\cos \chi} & {\sin \chi} \\ {- \sin \chi} & {\cos \chi} \\ \end{array}} \right).$$

(19)

Here we made use of the fact that any matrix can be written as the product of an orthogonal and a symmetric matrix, and that any symmetric matrix can be diagonalized. Note that, by our definition of infinitesimally thin bundles, D₊ and D₋ are non-zero almost everywhere. Equation (19) determines D₊ and D₋ up to sign. The most interesting case for us is that of an infinitesimally thin bundle that issues from a vertex at an observation event p_O into the past. For such bundles we require D₊ and D₋ to be positive near the vertex and differentiable everywhere; this uniquely determines D₊ and D₋ everywhere. With D₊ and D₋ fixed, the angles χ and ψ are unique at all points where the bundle is non-circular; in other words, requiring them to be continuous determines these angles uniquely along every infinitesimally thin bundle that is non-circular almost everywhere. In the representation of Equation (19), the extremal points of the bundle’s elliptical cross-section are given by the position vectors

$${Y_ +} = \cos \psi {Y_1} + \sin {Y_1} \simeq {D_ +}(\cos \chi {E_1} + \sin \chi {E_2}),$$

(20)

$${Y_ -} = - \sin \psi {Y_1} + \cos \psi {Y_2} \simeq {D_ -}(- \sin \chi {E_1} + \cos \chi {E_2}),$$

(21)

where ≃ means equality up to multiples of K. Hence, |D₊| and |D₋| give the semi-axes of the elliptical cross-section and χ gives the angle by which the ellipse is rotated with respect to the Sachs basis (see Figure 3). We call D₊, D₋, and χ the shape parameters of the bundle, following Frittelli, Kling, and Newman [121, 120]. Instead of D₊ and D₋ one may also use D₊D₋ and D₊/D₋. For the case that the infinitesimally thin bundle can be embedded in a wave front, the shape parameters D₊ and D₋ have the following interesting property (see Kantowski et al. [173, 84]). ${{\dot D}_ +}/{D_ +}$ and ${{\dot D}_ -}/{D_ -}$ give the principal curvatures of the wave front in the rest system of the observer field U which is perpendicular to the Sachs basis. The notation D₊ and D₋, which is taken from [84], is convenient because it often allows to write two equations in the form of one equation with a ± sign (see, e.g., Equation (27) or Equation (93) below). The angle χ can be directly linked with observations if a light source emits linearly polarized light (see Section 2.5). If the Sachs basis is transformed according to Equations (13, 14) and Y₁ and Y₂ are kept fixed, the Jacobi matrix changes according to ${{\tilde D}_ \pm} = {{\tilde D}_ \pm},\tilde {\mathcal X} = {\mathcal X} + \alpha, \psi = \psi$. This demonstrates the important fact that the shape and the size of the cross-section of an infinitesimally thin bundle has an invariant meaning [292].

2.3.5 Optical scalars

Along each infinitesimally thin bundle one defines the deformation matrix S by

$${{\dot D}} = {{DS}}.$$

(22)

This reduces the second-order linear differential equation (16) for D to a first-order non-linear differential equation for S,

$${{\dot S}} + {{SS}} = {{R}}.$$

(23)

It is usual to decompose S into antisymmetric, symmetric-tracefree, and trace parts,

$${{S}} = \left({\begin{array}{*{20}c} 0 & \omega \\ {- \omega} & 0 \\ \end{array}} \right) + \left({\begin{array}{*{20}c}{{\sigma _1}} & {{\sigma _2}} \\ {{\sigma _2}} & {- {\sigma _1}} \\ \end{array}} \right) + \left({\begin{array}{*{20}c}\theta & 0 \\ 0 & \theta \\ \end{array}} \right).$$

(24)

This defines the optical scalars ω (twist), φ (expansion), and (σ₁, σ₂) (shear). One usually combines them into two complex scalars ϱ = φ + iω and σ = σ₁ + iσ₂. A change (13, 14) of the Sachs basis affects the optical scalars according to $\tilde \varrho = \varrho$ and $\tilde \sigma = {e^{- 2i\alpha}}\sigma$. Thus, ϱ and |σ| are invariant. If rewritten in terms of the optical scalars, Equation (23) gives the Sachs equations

$$\dot \varrho = - {\varrho ^2} - \vert \sigma {\vert ^2} + {\Phi _{00}},$$

(25)

$$\dot \sigma = - \sigma (\varrho + \bar \varrho) + {\psi _0}.$$

(26)

One sees that the Ricci curvature term Φ₀₀ directly produces expansion (focusing) and that the conformal curvature term ψ₀ directly produces shear. However, as the shear appears in Equation (25), conformal curvature indirectly influences focusing (cf. Penrose [260]). With D written in terms of the shape parameters and S written in terms of the optical scalars, Equation (22) results in

$${\dot D_ \pm} - i\dot \chi {D_ \pm} = (\rho \pm {e^{2i\chi}}\sigma){D_ \pm}.$$

(27)

Along λ, Equations (25, 26) give a system of 4 real first-order differential equations for the 4 real variables ϱ and σ; if ϱ and σ are known, Equation (27) gives a system of 4 real first-order differential equations for the 4 real variables D_±, χ, and ψ. The twist-free solutions (g real) to Equations (25, 26) constitute a 3-dimensional linear subspace of the 4-dimensional space of all solutions. This subspace carries a natural metric of Lorentzian signature, unique up to a conformal factor, and was nicknamed Minikowski space in [20].

2.3.6 Conservation law

As the optical tidal matrix R is symmetric, for any two solutions D₁ and D₂ of the matrix Jacobi equation (16) we have

$${{{\dot D}}_1}{{D}}_2^T - {{{D}}_1}{{\dot D}}_2^T = {\rm{constant}},$$

(28)

where ()^T means transposition. Evaluating the case D₁ = D₂ shows that for every infinitesimally thin bundle

$$\omega {D_ +}{D_ -} = {\rm{constant}}.$$

(29)

Thus, there are two types of infinitesimally thin bundles: those for which this constant is non-zero and those for which it is zero. In the first case the bundle is twisting (ω ≠ 0 everywhere) and its cross-section nowhere collapses to a line or to a point (D₊ = 0 and D₋ = 0 everywhere). In the second case the bundle must be non-twisting (ω = 0 everywhere), because our definition of infinitesimally thin bundles implies that D₊ = 0 and D₋ = 0 almost everywhere. A quick calculation shows that ω = 0 is exactly the integrability condition that makes sure that the infinitesimally thin bundle can be embedded in a wave front. (For the definition of wave fronts see Section 2.2.) In other words, for an infinitesimally thin bundle we can find a wave front such that λ is one of the generators, and Y₁ and Y₂ connect λ with infinitesimally neighboring generators if and only if the bundle is twist-free. For a (necessarily twist-free) infinitesimally thin bundle, points where one of the two shape parameters D₊ and D₋ vanishes are called caustic points of multiplicity one, and points where both shape parameters D₊ and D₋ vanish are called caustic points of multiplicity two. This notion coincides exactly with the notion of caustic points, or conjugate points, of wave fronts as introduced in Section 2.2. The behavior of the optical scalars near caustic points can be deduced from Equation (27) with Equations (25, 26). For a caustic point of multiplicty one at s = s₀ one finds

$$\theta (s) = {1 \over {2(s - {s_0})}}(1 + {\mathcal O}(s - {s_0})),$$

(30)

$$\vert \sigma (s)\vert = {1 \over {2(s - {s_0})}}(1 + {\mathcal O}(s - {s_0})),$$

(31)

By contrast, for a caustic point of multiplicity two at s = s₀ the equations read (cf. [303])

$$\theta (s) = {1 \over {s - {s_0}}} + {\mathcal O}(s - {s_0}),$$

(32)

$$\sigma (s) = {1 \over 3}{\psi _0}({s_0})(s - {s_0}) + {\mathcal O}({(s - {s_0})^2}).$$

(33)

2.3.7 Infinitesimally thin bundles with vertex

We say that an infinitesimally thin bundle has a vertex at s = s₀ if the Jacobi matrix satisfies

$${{D}}({s_0}) = 0,\quad {{\dot D}}({s_0}) = 1.$$

(34)

A vertex is, in particular, a caustic point of multiplicity two. An infinitesimally thin bundle with a vertex must be non-twisting. While any non-twisting infinitesimally thin bundle can be embedded in a wave front, an infinitesimally thin bundle with a vertex can be embedded in a light cone. Near the vertex, it has a circular cross-section. If D₁ has a vertex at s₁ and D₂ has a vertex at s₂, the conservation law (28) implies

$${{D}}_2^T({s_1}) = - {{{D}}_1}({s_2}).$$

(35)

This is Etherington’s [104] reciprocity law. The method by which this law was proven here follows Ellis [97] (cf. Schneider, Ehlers, and Falco [299]). Etherington’s reciprocity law is of relevance, in particular in view of cosmology, because it relates the luminosity distance to the area distance (see Equation (47)). It was independently rediscovered in the 1960s by Sachs and Penrose (see [260, 190]).

The results of this section are the basis for Sections 2.4, 2.5, and 2.6.

2.4 Distance measures

In this section we summarize various distance measures that are defined in an arbitrary spacetime. Some of them are directly related to observable quantities with relevance for lensing. The material of this section makes use of the results on infinitesimally thin bundles which are summarized in Section 2.3. All of the distance measures to be discussed refer to a past-oriented lightlike geodesic λ from an observation event p_O to an emission event p_S (see Figure 4). Some of them depend on the 4-velocity U_O of the observer at p_O and/or on the 4-velocity U_S of the light source at p_S. If a vector field U with g(U, U) = −1 is distinguished on ${\mathcal M}$, we can choose for the observer an integral curve of U and for the light sources all other integral curves of U. Then each of the distance measures becomes a function of the observational coordinates (s, Ψ, Θ, τ) (recall Section 2.1).

Figure 4

Past-oriented lightlike geodesic λ from an observation event p_O to an emission event p_S. γ_O is the worldline of the observer, λ_S is the worldline of the light source. U_O is the 4-velocity of the observer at p_O and U_S is the 4-velocity of the light source at p_S.

2.4.1 Affine distance

There is a unique affine parametrization s ↦ λ(s) for each lightlike geodesic through the observation event p_O such that λ(0) = p_O and $g\left({\dot \lambda (0),{U_O}} \right) = 0$. Then the affine parameter s itself can be viewed as a distance measure. This affine distance has the desirable features that it increases monotonously along each ray and that it coincides in an infinitesimal neighborhood of p_O with Euclidean distance in the rest system of U_O. The affine distance depends on the 4-velocity U_O of the observer but not on the 4-velocity U_S of the light source. It is a mathematically very convenient notion, but it is not an observable. (It can be operationally realized in terms of an observer field whose 4-velocities are parallel along the ray. Then the affine distance results by integration if each observer measures the length of an infinitesimally short part of the ray in his rest system. However, in view of astronomical situations this is a purely theoretical construction.) The notion of affine distance was introduced by Kermack, McCrea, and Whittaker [180].

2.4.2 Travel time

As an alternative distance measure one can use the travel time. This requires the choice of a time function, i.e., of a function t that slices the spacetime into spacelike hypersurfaces t = constant. (Such a time function globally exists if and only if the spacetime is stably causal; see, e.g., [154], p. 198.) The travel time is equal to t(p_O) − t(p_S), for each p_S on the past light cone of p_O. In other words, the intersection of the light cone with a hypersurface t = constant determines events of equal travel time; we call these intersections “instantaneous wave fronts” (recall Section 2.2). Examples of instantaneous wave fronts are shown in Figures 13, 18, 19, 27, and 28. The travel time increases monotonously along each ray. Clearly, it depends neither on the 4-velocity U_O of the observer nor on the 4-velocity U_S of the light source. Note that the travel time has a unique value at each point of p_O’s past light cone, even at events that can be reached by two different rays from p_O. Near p_O the travel time coincides with Euclidean distance in the observer’s rest system only if U_O is perpendicular to the hypersurface t = constant with dt(U_O) = 1. (The latter equation is true if along the observer’s world line the time function t coincides with proper time.) The travel time is not directly observable. However, travel time differences are observable in multiple-imaging situations if the intrinsic luminosity of the light source is time-dependent. To illustrate this, think of a light source that flashes at a particular instant. If the flash reaches the observer’s wordline along two different rays, the proper time difference Δτ_O of the two arrival events is directly measurable. For a time function t that along the observer’s worldline coincides with proper time, this observed time delay Δτ_O gives the difference in travel time for the two rays. In view of applications, the measurement of time delays is of great relevance for quasar lensing. For the double quasar 0957+561 the observed time delay Δτ_O is about 417 days (see, e.g., [275], p. 149).

2.4.3 Redshift

In cosmology it is common to use the redshift as a distance measure. For assigning a redshift to a lightlike geodesic λ that connects the observation event p_O on the worldline γ_O of the observer with the emission event p_S on the worldline γ_S of the light source, one considers a neighboring lightlike geodesic that meets γ_O at a proper time interval Δτ_O from p_O and γ_S at a proper time interval Δτ_S from p_S. The redshift z is defined as

$$z = \underset {\Delta {\tau _{\rm{S}}} \rightarrow 0} {\lim} {{\Delta {\tau _{\rm{O}}} - \Delta {\tau _{\rm{S}}}} \over {\Delta {\tau _{\rm{S}}}}}.$$

(36)

If λ is affinely parametrized with λ(0) = p_O and λ(s) = p_S, one finds that z is given by

$$1 + z = {{g(\dot \lambda (0),{U_0})} \over {g(\dot \lambda (s),{U_{\rm{S}}})}}.$$

(37)

This general redshift formula is due to Kermack, McCrea, and Whittaker [180]. Their proof is based on the fact that $g(\dot \lambda, Y)$ is a constant for all Jacobi fields Y that connect λ with an infinitesimally neighboring lightlike geodesic. The same proof can be found, in a more elegant form, in [41] and in [312], p. 109. An alternative proof, based on variational methods, was given by Schrödinger [300]. Equation (37) is in agreement with the Hamilton formalism for photons. Clearly, the redshift depends on the 4-velocity U_O of the observer and on the 4-velocity U_S of the light source. If a vector field U with g(U, U) = −1 has been distinguished on ${\mathcal M}$, we may choose one integral curve of U as the observer and all other integral curves of U as the light sources. Then the redshift becomes a function of the observational coordinates (s, Ψ, Θ, τ). For s → 0, the redshift goes to 0,

$$z(s,\Psi, \Theta, \tau) = h(\Psi, \Theta, \tau)s + {\mathcal O}({s^2}),$$

(38)

with a (generalized) Hubble parameter h(Ψ, Θ, τ) that depends on spatial direction and on time. For criteria that h and the higher-order coefficients are independent of Ψ and Θ (see [152]). If the redshift is known for one observer field U, it can be calculated for any other U, according to Equation (37), just by adding the usual special-relativistic Doppler factors. Note that if U_O is given, the redshift can be made to zero along any one ray λ from p_O by choosing the 4-velocities U_λ(s) appropriately. This shows that z is a reasonable distance measure only for special situations, e.g., in cosmological models with U denoting the mean flow of luminous matter (“Hubble flow”). In any case, the redshift is directly observable if the light source emits identifiable spectral lines. For the calculation of Sagnac-like effects, the redshift formula (37) can be evaluated piecewise along broken lightlike geodesics [23].

2.4.4 Angular diameter distances

The notion of angular diameter distance is based on the intuitive idea that the farther an object is away the smaller it looks, according to the rule

$${\rm{object}}\,{\rm{diameter}} = {\rm{angle}} \times {\rm{distance}}.$$

(39)

The formal definition needs the results of Section 2.3 on infinitesimally thin bundles. One considers a past-oriented lightlike geodesic s → λ(s) parametrized by affine distance, i.e., λ(0) = p_O and $g\left({\dot \lambda (0),{U_O}} \right) = 1$, and along λ an infinitesimally thin bundle with vertex at the observer, i.e., at s = 0. Then the shape parameters D₊(s) and D₋(s) (recall Figure 3) satisfy the initial conditions D_±(0) = 0 and ${{\dot D}_ \pm}(0) = 1$. They have the following physical meaning. If the observer sees a circular image of (small) angular diameter α on his or her sky, the (small but extended) light source at affine distance s actually has an elliptical cross-section with extremal diameters α|D_±(s)|. It is therefore reasonable to call D₊ and D₋ the extremal angular diameter distances. Near the vertex, D₊ and D₋ are monotonously increasing functions of the affine distance, ${D_ \pm}(s) = (s) + {\mathcal O}({s^2})$. Farther away from the vertex, however, they may become decreasing, so the functions s ↦ D₊(s) and s ↦ D₋(s) need not be invertible. At a caustic point of multiplicity one, one of the two functions D₊ and D₋ changes sign; at a caustic point of multiplicity two, both change sign (recall Section 2.3). The image of a light source at affine distance s is said to have even parity if D₊(s)D₋(s) > 0 and odd parity if D₊(s)D₋(s) < 0. Images with odd parity show the neighborhood of the light source side-inverted in comparison to images with even parity. Clearly, D₊ and D₋ are reasonable distance measures only in a neighborhood of the vertex where they are monotonously increasing. However, the physical relevance of D₊ and D₋ lies in the fact that they relate cross-sectional diameters at the source to angular diameters at the observer, and this is always true, even beyond caustic points. D₊ and D₋ depend on the 4-velocity U_O of the observer but not on the 4-velocity U_S of the source. This reflects the fact that the angular diameter of an image on the observer’s sky is subject to aberration whereas the cross-sectional diameter of an infinitesimally thin bundle has an invariant meaning (recall Section 2.3). Hence, if the observer’s worldline γ_O has been specified, D₊ and D₋ are well-defined functions of the observational coordinates (s, Ψ, Θ, τ).

2.4.5 Area distance

The area distance D_area is defined according to the idea

$${\rm{object}}\,{\rm{area}} = {\rm{solid}}\,{\rm{angle}} \times {\rm{distanc}}{{\rm{e}}^2}.$$

(40)

As a formal definition for D_area, in terms of the extremal angular diameter distances D₊ and D₋ as functions of affine distance s, we use the equation

$$D\_\{{\rm{area}}\} (s) = \sqrt {\vert {D_ +}(s){D_ -}(s)\vert}.$$

(41)

D_area(s)² indeed relates, for a bundle with vertex at the observer, the cross-sectional area at the source to the opening solid angle at the observer. Such a bundle has a caustic point exactly at those points where D_area(s) = 0. The area distance is often called “angular diameter distance” although, as indicated by Equation (41), the name “averaged angular diameter distance” would be more appropriate. Just as D₊ and D₋, the area distance depends on the 4-velocity U_O of the observer but not on the 4-velocity U_S of the light source. The area distance is observable for a light source whose true size is known (or can be reasonably estimated). It is sometimes convenient to introduce the magnification or amplification factor

$$\mu(s) = {{{s^2}} \over {{D_ +}(s){D_ -}(s)}}.$$

(42)

The absolute value of μ determines the area distance, and the sign of μ determines the parity. In Minkowski spacetime, D_±(s) = s and, thus, μ(s) = 1. Hence, |μ(s)| > 1 means that a (small but extended) light source at affine distance s subtends a larger solid angle on the observer’s sky than a light source of the same size at the same affine distance in Minkowski spacetime. Note that in a multiple-imaging situation the individual images may have different affine distances. Thus, the relative magnification factor of two images is not directly observable. This is an important difference to the magnification factor that is used in the quasi-Newtonian approximation formalism of lensing. The latter is defined by comparison with an “unlensed image” (see, e.g., [299]), a notion that makes sense only if the metric is viewed as a perturbation of some “background” metric. One can derive a differential equation for the area distance (or, equivalently, for the magnification factor) as a function of affine distance in the following way. On every parameter interval where D₊D₋ has no zeros, the real part of Equation (27) shows that the area distance is related to the expansion by

$${\dot D_{{\rm{area}}}} = \theta {D_{{\rm{area}}}}.$$

(43)

Insertion into the Sachs equation (25) for θ = ϱ gives the focusing equation

$${\ddot D_{{\rm{area}}}} = \left({\vert \sigma {\vert ^2} + {1 \over 2}{\rm{Ric}}(\dot \lambda ,\dot \lambda)} \right){D_{{\rm{area}}}}.$$

(44)

Between the vertex at s = 0 and the first conjugate point (caustic point), D_area is determined by Equation (44) and the initial conditions

$${D_{{\rm{area}}}}(0) = 0,\quad {\dot D_{{\rm{area}}}}(0) = 1.$$

(45)

The Ricci term in Equation (44) is non-negative if Einstein’s field equation holds and if the energy density is non-negative for all observers (“weak energy condition”). Then Equations (44, 45) imply that

$${D_{{\rm{area}}}}(s) \leq s,$$

(46)

i.e., 1 ≤ μ(s), for all s between the vertex at s = 0 and the first conjugate point. In Minkowski spacetime, Equation (46) holds with equality. Hence, Equation (46) says that the gravitational field has a focusing, as opposed to a defocusing, effect. This is sometimes called the focusing theorem.

2.4.6 Corrected luminosity distance

The idea of defining distance measures in terms of bundle cross-sections dates back to Tolman [323] and Whittaker [351]. Originally, this idea was applied not to bundles with vertex at the observer but rather to bundles with vertex at the light source. The resulting analogue of the area distance is the so-called corrected luminosity distance D′_lum. It relates, for a bundle with vertex at the light source, the cross-sectional area at the observer to the opening solid angle at the light source. Owing to Etherington’s reciprocity law (35), area distance and corrected luminosity distance are related by

$$D_{{\rm{lum}}}{\prime} = (1 + z){D_{{\rm{area}}}}.$$

(47)

The redshift factor has its origin in the fact that the definition of D′_lum refers to an affine parametrization adapted to U_S, and the definition of D_area refers to an affine parametrization adapted to U_O. While D_area depends on U_O but not on U_S, D′_lum depends on U_S but not on U_O.

2.4.7 Luminosity distance

The physical meaning of the corrected luminosity distance is most easily understood in the photon picture. For photons isotropically emitted from a light source, the percentage that hit a prescribed area at the observer is proportional to 1/(D′_lum)². As the energy of each photon undergoes a redshift, the energy flux at the observer is proportional to 1/(D_lum)², where

$${D_{{\rm{lum}}}} = (1 + z){D\prime_{{\rm{lum}}}} = {(1 + z)^2}{D_{{\rm{area}}}}.$$

(48)

Thus, D_lum is the relevant quantity for calculating the luminosity (apparent brightness) of point-like light sources (see Equation (52)). For this reason D_lum is called the (uncorrected) luminosity distance. The observation that the purely geometric quantity D′_lum must be modified by an additional redshift factor to give the energy flux is due to Walker [342]. D_lum depends on the 4-velocity U_O of the observer and of the 4-velocity U_S of the light source. D_lum and D′_lum can be viewed as functions of the observational coordinates (s, Ψ, Θ, τ) if a vector field U with g(U, U) = −1 has been distinguished, one integral curve of U is chosen as the observer, and the other integral curves of U are chosen as the light sources. In that case Equation (38) implies that not only D_area(s) but also D_lum(s) and D′_lum(s) are of the form $s + {\mathcal O}({s^2})$. Thus, near the observer all three distance measures coincide with Euclidean distance in the observer’s rest space.

2.4.8 Parallax distance

In an arbitrary spacetime, we fix an observation event p_O and the observer’s 4-velocity U_O. We consider a past-oriented lightlike geodesic λ parametrized by affine distance, λ(0) = p_O and $g\left({\dot \lambda (0),{U_{\rm{O}}}} \right) = 1$. To a light source passing through the event λ(s) we assign the (averaged) parallax distance D_par(s) = −θ(0)⁻¹, where θ is the expansion of an infinitesimally thin bundle with vertex at λ(s). This definition follows [172]. Its relevance in view of cosmology was discussed in detail by Rosquist [289]. D_par can be measured by performing the standard trigonometric parallax method of elementary Euclidean geometry, with the observer at p_O and an assistant observer at the perimeter of the bundle, and then averaging over all possible positions of the assistant. Note that the method refers to a bundle with vertex at the light source, i.e., to light rays that leave the light source simultaneously. (Averaging is not necessary if this bundle is circular.) D_par depends on the 4-velocity of the observer but not on the 4-velocity of the light source. To within first-order approximation near the observer it coincides with affine distance (recall Equation (32)). For the potential obervational relevance of D_par see [289], and [299], p. 509.

In view of lensing, D₊, D₋, and D_lum are the most important distance measures because they are related to image distortion (see Section 2.5) and to the brightness of images (see Section 2.6). In spacetimes with many symmetries, these quantities can be explicitly calculated (see Section 4.1 for conformally flat spactimes, and Section 4.3 for spherically symmetric static spacetimes). This is impossible in a spacetime without symmetries, in particular in a realistic cosmological model with inhomogeneities (“clumpy universe”). Following Kristian and Sachs [190], one often uses series expansions with respect to s. For statistical considerations one may work with the focusing equation in a Friedmann-Robertson-Walker spacetime with average density (see Section 4.1), or with a heuristically modified focusing equation taking clumps into account. The latter leads to the so-called Dyer-Roeder distance [86, 87] which is discussed in several text-books (see, e.g., [299]). (For pre-Dyer-Roeder papers on optics in cosmological models with inhomogeneities, see the historical notes in [174].) As overdensities have a focusing and underdensities have a defocusing effect, it is widely believed (following [344]) that after averaging over sufficiently large angular scales the Friedmann-Robertson-Walker calculation gives the correct distance-redshift relation. However, it was argued by Ellis, Bassett, and Dunsby [99] that caustics produced by the lensing effect of overdensities lead to a systematic bias towards smaller angular sizes (“shrinking”). For a spherically symmetric inhomogeneity, the effect on the distance-redshift relation can be calculated analytically [230]. For thorough discussions of light propagation in a clumpy universe also see Pyne and Birkinshaw [283], and Holz and Wald [161].

2.5 Image distortion

In special relativity, a spherical object always shows a circular outline on the observer’s sky, independent of its state of motion [257, 321]. In general relativity, this is no longer true; a small sphere usually shows an elliptic outline on the observer’s sky. This distortion is caused by the shearing effect of the spacetime geometry on light bundles. For the calculation of image distortion we need the material of Sections 2.3 and 2.4. For an observer with 4-velocity U_O at an event p_O, there is a unique affine parametrization s ↦ λ(s) for each lightlike geodesic through p_O such that λ(0) = p_O and $g\left({\dot \lambda (0),{U_{\rm{O}}}} \right) = 1$. Around each of these λ we can consider an infinitesimally thin bundle with vertex at s = 0. The elliptical cross-section of this bundle can be characterized by the shape parameters D₊(s), D₋(s) and χ(s) (recall Figure 3). In the terminology of Section 2.4, s is the affine distance, and D₊(s) and D₋(s) are the extremal angular diameter distances. The complex quantity

$$\epsilon(s) = \left({{{{D_ +}(s)} \over {{D_ -}(s)}} - {{{D_ -}(s)} \over {{D_ +}(s)}}} \right){e^{- 2i\chi (s)}}$$

(49)

is called the ellipticity of the bundle. The phase of ϵ determines the position angle of the elliptical cross-section of the bundle with respect to the Sachs basis. The absolute value of ϵ(s) determines the eccentricity of this cross-section; ϵ(s) = 0 indicates a circular cross-section and |ϵ(s)| = ∞ indicates a caustic point of multiplicity one. (It is also common to use other measures for the eccentricity, e.g., |D₊ − D₋|/|D₊ + D₋|.) From Equation (27) with ϱ = θ we get the derivative of ϵ with respect to the affine distance s,

$$\dot \epsilon = 2\sigma \sqrt {\vert \epsilon{\vert ^2} + 4}.$$

(50)

The initial conditions ${D_ \pm}(0) = 0,\,{\dot D_ \pm}(0) = 1$ imply

$$\epsilon(0) = 0.$$

(51)

Equation (50) and Equation (51) determine e if the shear σ is known. The shear, in turn, is determined by the Sachs equations (25, 26) and the initial conditions (32, 33) with s₀ = 0 for θ(= ϱ) and σ.

It is recommendable to change from the ϵ determined this way to $\varepsilon = - \bar \epsilon$. This transformation corresponds to replacing the Jacobi matrix D by its inverse. The original quantity ϵ(s) gives the true shape of objects at affine distance s that show a circular image on the observer’s sky. The new quantity ε(s) gives the observed shape for objects at affine distance s that actually have a circular cross-section. In other words, if a (small) spherical body at affine distance s is observed, the ellipticity of its image on the observer’s sky is given by ε(s).

By Equations (50, 51), ϵ vanishes along the entire ray if and only if the shear σ vanishes along the entire ray. By Equations (26, 33), the shear vanishes along the entire ray if and only if the conformal curvature term ψ₀ vanishes along the entire ray. The latter condition means that $K = \dot \lambda$ is tangent to a principal null direction of the conformal curvature tensor (see, e.g., Chandrasekhar [54]). At a point where the conformal curvature tensor is not zero, there are at most four different principal null directions. Hence, the distortion effect vanishes along all light rays if and only if the conformal curvature vanishes everywhere, i.e., if and only if the spacetime is conformally flat. This result is due to Sachs [296]. An alternative proof, based on expressions for image distortions in terms of the exponential map, was given by Hasse [149].

For any observer, the distortion measure $\varepsilon = - \bar \epsilon$ is defined along every light ray from every point of the observer’s worldline. This gives ε as a function of the observational coordinates (s, Ψ, Θ, τ) (recall Section 2.1, in particular Equation (4)). If we fix τ and s, ε is a function on the observer’s sky. (Instead of s, one may choose any of the distance measures discussed in Section 2.4, provided it is a unique function of s.) In spacetimes with sufficiently many symmetries, this function can be explicitly determined in terms of integrals over the metric function. This will be worked out for spherically symmetric static spacetimes in Section 4.3. A general consideration of image distortion and example calculations can also be found in papers by Frittelli, Kling and Newman [121, 120]. Frittelli and Oberst [127] calculate image distortion by a “thick gravitational lens” model within a spacetime setting.

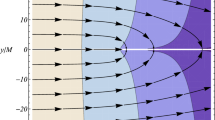
In cases where it is not possible to determine ε by explicitly integrating the relevant differential equations, one may consider series expansions with respect to the affine parameter s. This technique, which is of particular relevance in view of cosmology, dates back to Kristian and Sachs [190] who introduced image distortion as an observable in cosmology. In lowest non-vanishing order, ε(s, Ψ, Θ, τ_O) is quadratic with respect to s and completely determined by the conformal curvature tensor at the observation event p_O = γ(τ_O), as can be read from Equations (50, 51, 33). One can classify all possible distortion patterns on the observer’s sky in terms of the Petrov type of the Weyl tensor [56]. As outlined in [56], these patterns are closely related to what Penrose and Rindler [262] call the fingerprint of the Weyl tensor. At all observation events where the Weyl tensor is non-zero, the following is true. There are at most four points on the observer’s sky where the distortion vanishes, corresponding to the four (not necessarily distinct) principal null directions of the Weyl tensor. For type N, where all four principal null directions coincide, the distortion pattern is shown in Figure 5.

Figure 5

Distortion pattern. The picture shows, in a Mercator projection with Φ as the horizontal and Θ as the vertical coordinate, the celestial sphere of an observer at a spacetime point where the Weyl tensor is of Petrov type N. The pattern indicates the elliptical images of spherical objects to within lowest non-trivial order with respect to distance. The length of each line segment is a measure for the eccentricity of the elliptical image, the direction of the line segment indicates its major axis. The distortion effect vanishes at the north pole Θ = 0 which corresponds to the fourfold principal null direction. Contrary to the other Petrov types, for type N the pattern is universal up to an overall scaling factor. The picture is taken from [56] where the distortion patterns for the other Petrov types are given as well.

The distortion effect is routinely observed since the mid-1980s in the form of arcs and (radio) rings (see [299, 275, 343] for an overview). In these cases a distant galaxy appears strongly elongated in one direction. Such strong elongations occur near a caustic point of multiplicity one where |ε| → ∞. In the case of rings and (long) arcs, the entire bundle cannot be treated as infinitesimally thin, i.e., a theoretical description of the effect requires an integration. For the idealized case of a point source, images in the form of (1-dimensional) rings on the observer’s sky occur in cases of rotational symmetry and are usually called “Einstein rings” (see Section 4.3). The rings that are actually observed show extended sources in situations close to rotational symmetry.

For the majority of galaxies that are not distorted into arcs or rings, there is a “weak lensing” effect on the apparent shape that can be investigated statistically. The method is based on the assumption that there is no prefered direction in the universe, i.e., that the axes of (approximately spheroidal) galaxies are randomly distributed. So, without a distortion effect, the axes of galaxy images should make a randomly distributed angle with the (Ψ, Θ) grid on the observer’s sky. Any deviation from a random distribution is to be attributed to a distortion effect, produced by the gravitational field of intervening masses. With the help of the quasi-Newtonian approximation, this method has been elaborated into a sophisticated formalism for determining mass distributions, projected onto the plane perpendicular to the line of sight, from observed image distortions. This is one of the most important astrophysical tools for detecting (dark) matter. It has been used to determine the mass distribution in galaxies and galaxy clusters, and more recently observations of image distortions produced by large-scale structure have begun (see [22] for a detailed review). From a methodological point of view, it would be desirable to analyse this important line of astronomical research within a spacetime setting. This should give prominence to the role of the conformal curvature tensor.

Another interesting way of observing weak image distortions is possible for sources that emit linearly polarized radiation. (This is true for many radio galaxies. Polarization measurements are also relevant for strong-lensing situations; see Schneider, Ehlers, and Falco [299], p. 82 for an example.) The method is based on the geometric optics approximation of Maxwell’s theory. In this approximation, the polarization vector is parallel along each ray between source and observer [88] (cf., e.g., [225], p. 577). We may, thus, use the polarization vector as a realization of the Sachs basis vector E₁. If the light source is a spheroidal celestial body (e.g., an elliptic galaxy), it is reasonable to assume that at the light source the polarization direction is aligned with one of the axes, i.e., 2χ(s)/π ∈ ℤ. A distortion effect is verified if the observed polarization direction is not aligned with an axis of the image, 2χ(0)/π ∉ ℤ. It is to be emphasized that the deviation of the polarization direction from the elongation axis is not the result of a rotation (the bundles under consideration have a vertex and are, thus, twist-free) but rather of successive shearing processes along the ray. Also, the effect has nothing to do with the rotation of an observer field. It is a pure conformal curvature effect. Related misunderstandings have been clarified by Panov and Sbytov [254, 255]. The distortion effect on the polarization plane has, so far, not been observed. (Panov and Sbytov [254] have clearly shown that an effect observed by Birch [31], even if real, cannot be attributed to distortion.) Its future detectability is estimated, for distant radio sources, in [318].

2.6 Brightness of images

For calculating the brightness of images we need the definitions and results of Section 2.4. In particular we need the luminosity distance D_lum and its relation to other distance measures. We begin by considering a point source (worldline) that emits isotropically with (bolometric, i.e., integrated over all frequencies) luminosity L. By definition of D_lum, in this case the energy flux at the observer is

$$F = {1 \over {4\pi {D_{{\rm{lum}}}}2}}.$$

(52)

F is a measure for the brightness of the image on the observer’s sky. The magnitude m used by astronomers is essentially the negative logarithm of F,

$$m = 2.5{\log _{10}}({D_{{\rm{lum}}}}^2) - 2.5{\log _{10}}(L) + {m_0},$$

(53)

with m₀ being a universal constant. In Equation (52), D_lum can be expresed in terms of the area distance D_area and the redshift z with the help of the general relation (48). This demonstrates that the magnification factor μ, which is defined by Equation (42), admits the following reinterpretation. |μ(s)| relates the flux from a point source at affine distance s to the flux from a point source with the same luminosity at the same affine distance and at the same redshift in Minkowski spacetime.

D_lum can be explicitly calculated in spacetimes where the Jacobi fields along lightlike geodesics can be explicitly determined. This is true, e.g., in spherically symmetric and static spacetimes where the extremal angular diameter distances D₊ and D₋ can be calculated in terms of integrals over the metric coefficients. The resulting formulas are given in Section 4.3 below. Knowledge of D₊ and D₋ immediately gives the area distance D_area via Equation (41). D_area together with the redshift determines D_lum via Equation (48). Such an explicit calculation is, of course, possible only for spacetimes with many symmetries.

By Equation (48), the zeros of D_lum coincide with the zeros of D_area, i.e., with the caustic points. Hence, in the ray-optical treatment a point source is infinitely bright (magnitude m = −∞) if it passes through the caustic of the observer’s past light cone. A wave-optical treatment shows that the energy flux at the observer is actually bounded by diffraction. In the quasi-Newtonian approximation formalism, this was demonstrated by an explicit calculation for light rays deflected by a spheroidal mass by Ohanian [245] (cf. [299], p. 220). Quite generally, the ray-optical calculation of the energy flux gives incorrect results if, for two different light paths from the source worldline to the observation event, the time delay is smaller than or approximately equal to the coherence time. Then interference effects give rise to frequency-dependent corrections to the energy flux that have to be calculated with the help of wave optics. In multiple-imaging situations, the time delay decreases with decreasing mass of the deflector. If the deflector is a cluster of galaxies, a galaxy, or a star, interference effects can be ignored. Gould [145] suggested that they could be observable if a deflector of about 10⁻¹⁵ Solar masses happens to be close to the line of sight to a gamma-ray burster. In this case, the angle-separation between the (unresolvable) images would be of the order 10⁻¹⁵ arcseconds (“femtolensing”). Interference effects could make a frequency-dependent imprint on the total intensity. Ulmer and Goodman [328] discussed related effects for deflectors of up to 10⁻¹¹ Solar masses. Femtolensing has not been observed so far. However, it is an interesting future perspective for lensing effects where wave optics has to be taken into account. This would give practical relevance to the theoretical work of Herlt and Stephani [156, 157] who calculated gravitational lensing on the basis of wave optics in the Schwarzschild spacetime.

We now turn to the case of an extended source, whose surface makes up a 3-dimensional timelike submanifold ${\mathcal T}$ of the spacetime. In this case the radiation is characterized by the surface brightness B (= luminosity L per area) at the source and by the intensity I (= energy flux F per solid angle) at the observer. For each past-oriented light ray from an observation event p_O and to an event p_S on ${\mathcal T}$, we can relate B and I in the following way. By definition, the area distance D_area relates the area at the source to the solid angle at the observer, so we get from Equation (52) $I = B{D_{{\rm{area}}}}^2/{D_{{\rm{lum}}}}^2$. As area distance and luminosity distance are related by a redshift factor, according to the general law (48), this gives the relation

$$I = {B \over {4\pi {{(1 + z)}^4}}}.$$

(54)

This result is, of course, valid only if the radiation from different parts of the emitting surface is incoherent; otherwise interference effects have to be taken into account. The most remarkable feature of Equation (54) is that all distance measures have dropped out. Save for a redshift factor, the (observed) intensity of a radiating surface is the same for all observers.

The law for point sources (52) and the law for extended sources (54) refer to bolometric quantities, i.e., to integration over all frequencies. As every astronomical observation is restricted to a certain frequency range, it is actually necessary to consider frequency-specific quantities. For a point source, one writes $L = \int\nolimits_0^\infty \ell ({\omega _{\rm{S}}})d{\omega _{\rm{S}}}$ and $F = \int\nolimits_0^\infty f({\omega _{\rm{O}}})d{\omega _{\rm{O}}}$, where the specific luminosity ℓ is a function of the emitted frequency ω_S and the specific flux f is a function of the received frequency ω_O. As ω_S and ω_O are related by a redshift factor, the frequency-specific version of Equation (52) reads

$$f({\omega _{\rm{O}}}) = {{\ell ({\omega _{\rm{O}}}(1 + z))(1 + z)} \over {4\pi {D_{{\rm{lum}}}}^2}}.$$

(55)

Similarly, for an extended source one introduces a specific surface brightness b and a specific intensity i such that $B = \int\nolimits_0^\infty b({\omega _{\rm{S}}})d{\omega _{\rm{S}}}$ and $I = \int\nolimits_0^\infty i({\omega _{\rm{O}}})d{\omega _{\rm{O}}}$. Then one gets the following frequency-specific version of Equation (54).

$$i({\omega _{\rm{O}}}) = {{b({\omega _{\rm{O}}}(1 + z))} \over {4\pi {{(1 + z)}^3}}}.$$

(56)

The results summarized in this section can also be derived from the kinetic theory of photons (see, e.g., [89]). In the photon picture, the three redshift factors in Equation (56) are easily understood: The first reflects the fact that each photon undergoes a redshift; the second relates the rate of emission (with respect to proper time at the source) to the rate of reception (with respect to proper time at the obsever); the third reflects the aberration effect on the angular size of the source in dependence of the motion of the observer.

As an example for the calculation of the brightness of images we consider the Schwarzschild spactime (see Figure 17).

2.7 Conjugate points and cut points

In general, the past light cone of an event forms caustics and transverse self-intersections, i.e., it is neither an embedded nor an immersed submanifold. The relevance of this fact in view of lensing was emphasized already in Section 2.1. In the following we demonstrate that caustics and transverse self-intersections of the light cone are related to extremizing properties of lightlike geodesics. A light cone with a caustic and a transverse self-intersection is shown in Figure 25.

In this section and in Section 2.8 we use mathematical techniques which are related to the Penrose-Hawking singularity theorems. For background material, see Penrose [261], Hawking and Ellis [154], O’Neill [247], and Wald [341].

Recall from Section 2.2 that the caustic of the past light cone of p_O is the set of all points where this light cone is not an immersed submanifold. A point p_S is in the caustic if a generator λ of the light cone intersects at p_S an infinitesimally neighboring generator. In this situation p_S is said to be conjugate to p_O along λ. The caustic of the past light cone of p_O is also called the “past lightlike conjugate locus” of p_O.

The notion of conjugate points is related to the extremizing properties of lightlike geodesics in the following way. Let λ be a past-oriented lightlike geodesic with λ(0) = p_O. Assume that p_S = λ(s₀) is the first conjugate point along this geodesic. This means that p_S is in the caustic of the past light cone of p_O and that λ does not meet the caustic at parameter values between 0 and s₀. Then a well-known theorem says that all points λ(s) with 0 < s < s₀ cannot be reached from p_O along a timelike curve arbitrarily close to λ, and all points λ(s) with s > s₀ can. For a proof we refer to Hawking and Ellis [154], Proposition 4.5.11 and Proposition 4.5.12. It might be helpful to consult O’Neill [247], Chapter 10, Proposition 48, in addition.

Here we have considered a past-oriented lightlike geodesic because this is the situation with relevance to lensing. Actually, Hawking and Ellis consider the time-reversed situation, i.e., with λ future-oriented. Then the result can be phrased in the following way. A material particle may catch up with a light ray λ after the latter has passed through a conjugate point and, for particles staying close to λ, this is impossible otherwise. The restriction to particles staying close to λ is essential. Particles “taking a short cut” may very well catch up with a lightlike geodesic even if the latter is free of conjugate points.

For a discussion of the extremizing property in the global sense, not restricted to timelike curves close to λ, we need the notion of cut points. The precise definition of cut points reads as follows.

As ususal, let I⁻(p_O) denote the chronological past of p_O, i.e., the set of all $q \in {\mathcal M}$ that can be reached from p_O along a past-pointing timelike curve. In Minkowski spacetime, the boundary ∂I⁻(p_O) of I^∂(p_O) is just the past light cone of p_O united with {p_O}. In an arbitrary spacetime, this is not true. A lightlike geodesic λ that issues from p_O into the past is always confined to the closure of I−(p_O), but it need not stay on the boundary. The last point on λ that is on the boundary is by definition [46] the cut point of λ. In other words, it is exactly the part of λ beyond the cut point that can be reached from p_O along a timelike curve. The union of all cut points, along any past-pointing lightlike geodesic λ from p_O, is called the cut locus of the past light cone (or the past lightlike cut locus of p_O). For the light cone in Figure 24 this is the curve (actually 2-dimensional) where the two sheets of the light cone intersect. For the light cone in Figure 25 the cut locus is the same set plus the swallow-tail point (actually 1-dimensional). For a detailed discussion of cut points in manifolds with metrics of Lorentzian signature, see [25]. For positive definite metrics, the notion of cut points dates back to Poincaré [280] and Whitehead [350].

For a generator λ of the past light cone of p_O, the cut point of λ does not exist in either of the two following cases:

• 1. λ always stays on the boundary ∂I⁻(p_O), i.e., it never loses its extremizing property.

• 2. λ is always in I⁻(p_O), i.e., it fails to be extremizing from the very beginning.

Case 2 occurs, e.g., if there is a closed timelike curve through p_O. More precisely, Case 2 is excluded if the past distinguishing condition is satisfied at p_O, i.e., if for $q \in {\mathcal M}$ the implication

$${I^ -}(q) = {I^ -}({p_{\rm{O}}}) \Rightarrow q = {p_0}$$

(57)

holds. If Equation (57) is true, the following can be shown:

• (P1) If, along λ, the point λ(s) is conjugate to λ(0), the cut point of λ exists and it comes on or before λ(s).

• (P2) Assume that a point q can be reached from p_O along two different lightlike geodesics λ₁ and λ₂ from p_O. Then the cut point of λ₁ and of λ₂ exists and it comes on or before q.

• (P3) If the cut locus of a past light cone is empty, this past light cone is an embedded submanifold of ${\mathcal M}$.

For proofs see [268]; The proofs can also be found in or easily deduced from [25]. Statement (P1) says that conjugate points and cut points are related by the easily remembered rule “the cut point comes first”. Statement (P2) says that a “cut” between two geodesics is indicated by the occurrence of a cut point. However, it does not say that exactly at the cut point a second geodesic is met. Such a stronger statement, which truly justifies the name “cut point”, holds in globally hyperbolic spacetimes (see Section 3.1). Statement (P3) implies that the occurrence of transverse self-intersections of a light cone are always indicated by cut points. Note, however, that transverse self-intersections of the past light cone of p_O may occur inside I⁻ (p_O) and, thus, far away from the cut locus.

Statement (P1) implies that dI⁻(p_O) is an immersed submanifold everywhere except at the cut locus and, of course, at the vertex p_O. It is known (see [154], Proposition 6.3.1) that ∂I⁻(p_O) is achronal (i.e., it is impossible to connect any two of its points by a timelike curve) and thus a 3-dimensional Lipschitz topological submanifold. By a general theorem of Rademacher (see [113], Theorem 3.6.1), this implies that ∂I⁻(p_O) is differentiable almost everywhere, i.e., that the cut locus has measure zero in ∂I⁻(p_O). Note that this argument does not necessarily imply that the cut locus is a “small” subset of ∂I⁻(p_O). Chruściel and Galloway [57] have demonstrated, by way of example, that an achronal subset ${\mathcal A}$ of a spacetime may fail to be differentiable on a set that is dense in ${\mathcal A}$. So our reasoning so far does not even exclude the possibility that the cut locus is dense in an open subset of ∂I⁻(p_O). This possibility can be excluded in globally hyperbolic spacetimes where the cut locus is always a closed subset of ${\mathcal M}$ (see Section 3.1). In general, the cut locus need not be closed as is exemplified by Figure 24.

In Section 2.8 we investigate the relevance of cut points (and conjugate points) for multiple imaging.

2.8 Criteria for multiple imaging

To investigate whether multiple imaging occurs in a spacetime (${\mathcal M},g$), we choose any point p_O (observation event) and any timelike curve γ_S (wordline of light source) in ${\mathcal M}$. The following cases are possible:

• 1. There is no past-pointing lightlike geodesic from p_O to γ_S. Then the observer at p_O does not see any image of the light source γ_S. For instance, this occurs in Minkowski spacetime for an inextendible worldline γ_S that asymptotically approaches the past light cone of p_O.

• 2. There is exactly one past-pointing lightlike geodesic from p_O to γ_S. Then the observer at p_S sees exactly one image of the light source γ_S. This is the situation naively taken for granted in pre-relativistic astronomy.

• 3. There are at least two but not more than denumerably many past-pointing lightlike geodesics from p_O to γ_S. Then the observer at p_O sees finitely or infinitely many distinct images of γ_O at his or her celestial sphere.

• 4. There are more than denumerably many past-pointing lightlike geodesics from p to γ. This happens, e.g., in rotationally symmetric situations where it gives rise to the so-called “Einstein rings” (see Section 4.3). It also happens, e.g., in plane-wave spacetimes (see Section 5.11).

If Case 3 or 4 occurs, astronomers speak of multiple imaging. We first demonstrate that Case 4 is exceptional. It is easy to prove (see, e.g., [268], Proposition 12) that no finite segment of the timelike curve γ_S can be contained in the past light cone of p_O. Thus, if there is a continuous one-parameter family of lightlike geodesics that connect p_O and γ_O, then all family members meet γ_S at the same point, say p_S. This point must be in the caustic of the light cone because through all non-caustic points there is only a discrete number of generators. One can always find a point p′_O arbitrarily close to p_O such that γ_S does not meet the caustic of the past light cone of p′_O (see, e.g., [268], Proposition 10). Hence, by an arbitrarily small perturbation of p_O one can always destroy a Case 4 situation. One may interpret this result as saying that Case 4 situations have zero probability. This is, indeed, true as long as we consider point sources (worldlines). The observed rings and arcs refer to extended sources (worldtubes) which are close to the caustic (recall Section 2.5). Such situations occur with non-zero probability.

We will now show how multiple imaging is related to the notion of cut points (recall Section 2.7). For any point p_O in an arbitrary spacetime, the following criteria for multiple imaging hold:

• (C1) Let λ be a past-pointing lightlike geodesic from p_O and let p_S be a point on λ beyond the cut point or beyond the first conjugate point. Then there is a timelike curve γ_S through p_S that can be reached from p_O along a second past-pointing lightlike geodesic.

• (C2) Assume that at p_O the past-distinguishing condition (57) is satisfied. If a timelike curve γ_S can be reached from p_O along two different past-pointing lightlike geodesics, at least one of them passes through the cut locus of the past light cone of p_O on or before arriving at γ_S.

For proofs see [267] or [268]. (In [267] Criterion (C2) is formulated with the strong causality condition, although the past-distinguishing condition is sufficient.) Criteria (C1) and (C2) say that the occurrence of cut points is sufficient and, in past-distinguishing spacetimes, also necessary for multiple imaging. The occurrence of conjugate points is sufficient but, in general, not necessary for multiple imaging (see Figure 24 for an example without conjugate points where multiple imaging occurs). In Section 3.1 we will see that in globally hyperbolic spacetimes conjugate points are necessary for multiple imaging. So we have the following diagram:

Table 1

It is well known (see [154], in particular Proposition 4.4.5) that, under conditions which are to be considered as fairly general from a physical point of view, a lightlike geodesic must either be incomplete or contain a pair of conjugate points. These “fairly general conditions” are, e.g., the weak energy condition and the so-called generic condition (see [154] for details). This result implies the occurrence of conjugate points and, thus, of multiple imaging, for a large class of spacetimes.

The occurrence of conjugate points has an important consequence in view of the focusing equation for the area distance D_area (recall Section 2.4 and, in particular, Equation (44)). As D_area vanishes at the vertex s = 0 and at each conjugate point, there must be a parameter value s_m with Ḋ_area(s_m) = 0 between the vertex and the first conjugate point. An elementary evaluation of the focusing equation (44) then implies

$$1 \leq \int\nolimits_0^{{s_m}} s \left({\vert \sigma (s){\vert ^2} + \left\vert {{1 \over 2}{\rm{Ric}}(\dot \lambda (s),\dot \lambda (s))} \right\vert} \right)ds.$$

(58)

As the Ricci term is related to the energy density via Einstein’s field equation, (58) gives an estimate of energy-density-plus-shear along the ray. If we observe a multiple imaging situation, and if we know (or assume) that we are in a situation where conjugate points are necessary for multiple imaging, we have thus an estimate on energy-density-plus-shear along the ray. This line of thought was worked out, under additional assumptions on the spacetime, in [250].

2.9 Fermat’s principle for light rays

It is often advantageous to characterize light rays by a variational principle, rather than by a differential equation. This is particularly true in view of applications to lensing. If we have chosen a point p_O (observation event) and a timelike curve γ_S (worldline of light source) in spacetime ${\mathcal M}$, we want to determine all past-pointing lightlike geodesics from p_O to γ_S. When working with a differential equation for light rays, we have to calculate all light rays issuing from p_O into the past, and to see which of them meet γ_S. If we work with a variational principle, we can restrict to curves from p_O to γ_S at the outset.

To set up a variational principle, we have to choose the trial curves among which the solution curves are to be determined and the functional that has to be extremized. Let ${{\mathcal L}_{{p_{\rm{O}}},\gamma {\rm{s}}}}$ denote the set of all past-pointing lightlike curves from p_O to γ_S. This is the set of trial curves from which the lightlike geodesics are to be singled out by the variational principle. Choose a past-oriented but otherwise arbitrary parametrization for the timelike curve γ_S and assign to each trial curve the parameter at which it arrives. This gives the arrival time functional T: ${{\mathcal L}_{{p_{\rm{O}}},\gamma {\rm{s}}}} \rightarrow {\mathbb R}$ that is to be extremized. With respect to an appropriate differentiability notion for T, it turns out that the critical points (i.e., the points where the differential of T vanishes) are exactly the geodesics in ${{\mathcal L}_{{p_{\rm{O}}},\gamma {\rm{s}}}}$. This result (or its time-reversed version) can be viewed as a general-relativistic Fermat principle:

Among all ways to move from p_O to γ_S in the past-pointing (or future-pointing) direction at the speed of light, the actual light rays choose those paths that make the arrival time stationary.

This formulation of Fermat’s principle was suggested by Kovner [187]. The crucial idea is to refer to the arrival time which is given only along the curve γ_S, and not to some kind of global time which in an arbitrary spacetime does not even exist. The proof that the solution curves of Kovner’s variational principle are, indeed, exactly the lightlike geodesics was given in [264]. The proof can also be found, with a slight restriction on the spacetime that simplifies matters considerably, in [299]. An alternative version, based on making ${{\mathcal L}_{{p_{\rm{O}}},\gamma {\rm{s}}}}$ into a Hilbert manifold, is given in [266].

As in ordinary optics, the light rays make the arrival time stationary but not necessarily minimal. A more detailed investigation shows that for a geodesic $\lambda \in {{\mathcal L}_{p{\rm{o}}\gamma {\rm{s}}}}$ the following holds. (For the notion of conjugate points see Sections 2.2 and 2.7.)

• (A1) If along λ there is no point conjugate to p_O, λ is a strict local minimum of T.

• (A2) If λ passes through a point conjugate to p_O before arriving at γ, it is a saddle of T.

• (A3) If λ reaches the first point conjugate to p_O exactly on its arrival at γ_S, it may be a local minimum or a saddle but not a local maximum.

For a proof see [264] or [266]. The fact that local maxima cannot occur is easily understood from the geometry of the situation: For every trial curve we can find a neighboring trial curve with a larger T by putting “wiggles” into it, preserving the lightlike character of the curve. Also for Fermat’s principle in ordinary optics, the extremum is never a local maximum, as is mentioned, e.g., in Born and Wolf [35], p. 137.

The advantage of Kovner’s version of Fermat’s principle is that it works in an arbitrary spacetime. In particular, the spacetime need not be stationary and the light source may arbitrarily move around (at subluminal velocity, of course). This allows applications to dynamical situations, e.g., to lensing by gravitational waves (see Section 5.11). If the spacetime is stationary or conformally stationary, and if the light source is at rest, a purely spatial reformulation of Fermat’s principle is possible. This more specific version of Femat’s principle is known since decades and has found various applications to lensing (see Section 4.2). A more sophisticated application of Fermat’s principle to lensing theory is to put up a Morse theory in order to prove theorems on the possible number of images. In its strongest version, this approach has to presuppose a globally hyperbolic spacetime and will be reviewed in Section 3.3.

For a generalization of Kovner’s version of Fermat’s principle to the case that observer and light source have a spatial extension (see [272]).

An alternative variational principle was introduced by Frittelli and Newman [123] and evaluated in [124, 12]. While Kovner’s principle, like the classical Fermat principle, is a varional principle for rays, the Frittelli-Newman principle is a variational principle for wave fronts. (For the definition of wave fronts see Section 2.2.) Although Frittelli and Newman call their variational principle a version of Fermat’s principle, it is actually closer to the classical Huygens principle than to the classical Fermat principle. Again, one fixes p_O and γ_S as above. To define the trial maps, one chooses a set ${\mathcal W}({p_{\rm{O}}})$ of wave fronts, such that for each lightlike geodesic through p_O there is exactly one wave front in ${\mathcal W}({p_{\rm{O}}})$ that contains this geodesic. Hence, ${\mathcal W}({p_{\rm{O}}})$ is in one-to-one correspondence to the lightlike directions at p_O and thus to the 2-sphere. Now let ${\mathcal W}({p_{\rm{O}}},{\gamma _{\rm{s}}})$ denote the set of all wave fronts in ${\mathcal W}({p_{\rm{O}}})$ that meet γ_S. We can then define the arrival time functional $T:{\mathcal W}({p_{\rm{O}}},{\gamma _{\rm{s}}}) \rightarrow {\mathbb R}$ by assigning to each wave front the parameter value at which it intersects γ_S. There are some cases to be excluded to make sure that T is defined on an open subset of ${\mathcal W}({p_{\rm{O}}}) \simeq {S^2}$, single-valued and differentiable. If this is the case, one finds that T is stationary at $W \in {\mathcal W}({p_{\rm{O}}})$ if and only if W contains a lightlike geodesic from p_O to γ_S. Thus, to each image of γ_S on the sky of po there corresponds a critical point of T. The great technical advantage of the Frittelli-Newman principle over the Kovner principle is that T is defined on a finite dimensional manifold, directly to be identified with (part of) the observer’s celestial sphere. The arrival time T in the Frittelli-Newman approach is directly analogous to the “Fermat potential” in the quasi-Newtonian formalism which is discussed, e.g., in [299]. In view of applications, a crucial point is that the space ${\mathcal W}({p_{\rm{O}}})$ is a matter of choice; there are many wave fronts which have one light ray in common. There is a natural choice, e.g., in asymptotically simple spacetimes (see Section 3.4).

Frittelli, Newman, and collaborators have used their variational principle in combination with the exact lens map (recall Section 2.1) to discuss thick and thin lens models from a spacetime perspective [ 24, 12 ]. Methods from differential topology or global analysis, e.g., Morse theory, have not yet been applied to the Frittelli-Newman principle.

3 Lensing in Globally Hyperbolic Spacetimes

In a globally hyperbolic spacetime, considerably stronger statements on qualitative lensing features can be made than in an arbitrary spacetime. This includes, e.g., multiple imaging criteria in terms of cut points or conjugate points, and also applications of Morse theory. The value of these results lies in the fact that they hold in globally hyperbolic spacetimes without symmetries, where lensing cannot be studied by explicitly integrating the lightlike geodesic equation.

The most convenient formal definition of global hyperbolicity is the following. In a spacetime (${\mathcal M},g$), a subset ${\mathcal C}$ of ${\mathcal M}$ is called a Cauchy surface if every inextendible causal (i.e., timelike or lightlike) curve intersects ${\mathcal C}$ exactly once. A spacetime is globally hyperbolic if and only if it admits a Cauchy surface. The name globally hyperbolic refers to the fact that for hyperbolic differential equations, like the wave equation, existence and uniqueness of a global solution is guaranteed for initial data given on a Cauchy surface. For details on globally hyperbolic spacetimes see, e.g., [154, 25]. It was demonstrated by Geroch [133] that every gobally hyperbolic spacetime admits a continuous function $t:{\mathcal M} \rightarrow {\mathbb R}$ such that t⁻¹(t₀) is a Cauchy surface for every t₀ ∈ ℝ. A complete proof of the fact that such a Cauchy time function can be chosen differentiable was given much later by Bernal and Sánchez [27, 26]. The topology of a globally hyperbolic spacetime is determined by the topology of any of its Cauchy surfaces, ${\mathcal M} \simeq {\mathcal C} \times {\mathbb R}$. Note, however, that the converse is not true because ${{\mathcal C}_1} \times {\mathbb R}$ may be homeomorphic (and even diffeomorphic) to ${{\mathcal C}_2} \times {\mathbb R}$ without ${{\mathcal C}_1}$ being homeomorphic to ${{\mathcal C}_2}$. For instance, one can construct a globally hyperbolic spacetime with topology ℝ⁴ that admits a Cauchy surface which is not homeomorphic to ℝ³ [238].

In view of applications to lensing the following observation is crucial. If one removes a point, a worldline (timelike curve), or a world tube (region with timelike boundary) from an arbitrary spacetime, the resulting spacetime cannot be globally hyperbolic. Thus, restricting to globally hyperbolic spacetimes excludes all cases where a deflector is treated as non-transparent by cutting its world tube from spacetime (see Figure 24 for an example). Note, however, that this does not mean that globally hyperbolic spacetimes can serve as models only for transparent deflectors. First, a globally hyperbolic spacetime may contain “non-transparent” regions in the sense that a light ray may be trapped in a spatially compact set. Second, the region outside the horizon of a (Schwarzschild, Kerr, …) black hole is globally hyperbolic.

3.1 Criteria for multiple imaging in globally hyperbolic spacetimes

In Section 2.7 we have considered the past light cone of an event p_O in an arbitrary spacetime. We have seen that conjugate points (= caustic points) indicate that the past light cone fails to be an immersed submanifold and that cut points indicate that it fails to be an embedded submanifold. In a globally hyperbolic spacetime (${\mathcal M},g$), the following additional statements are true.

• (H1) The past light cone of any event p_O, together with the vertex {p_O}, is closed in ${\mathcal M}$.

• (H2) The cut locus of the past light cone of p_O is closed in ${\mathcal M}$.

• (H3) Let p_S be in the cut locus of the past light cone of p_O but not in the conjugate locus (= caustic). Then p_S can be reached from p_O along two different lightlike geodesics. The past light cone of p_O has a transverse self-intersection at p_S.

• (H4) The past light cone of p_O is an embedded submanifold if and only if its cut locus is empty.

Analogous results hold, of course, for the future light cone, but the past version is the one that has relevance for lensing. For proofs of these statements see [25], Propositions 9.35 and 9.29 and Theorem 9.15, and [268], Propositions 13, 14, and 15. According to Statement (H3), a “cut point” indicates a “cut” of two lightlike geodesics. For geodesics in Riemannian manifolds (i.e., in the positive definite case), an analogous statement holds if the Riemannian metric is complete and is known as Poincaré theorem [280, 350]. It was this theorem that motivated the name “cut point”. Note that Statement (H3) is not true without the assumption that p_S is not in the caustic. This is exemplified by the swallow-tail point in Figure 25. However, as points in the caustic of the past light cone of p_O can be reached from p_O along two “infinitesimally close” lightlike geodesics, the name “cut point” may be considered as justified also in this case.

In addition to Statemens (H1) and (H2) one would like to know whether in globally hyperbolic spactimes the caustic of the past light cone of p_O (also known as the past lightlike conjugate locus of p_O) is closed. This question is closely related to the question of whether in a complete Riemannian manifold the conjugate locus of a point is closed. For both questions, the answer was widely believed to be ‘yes’ although actually it is ‘no’. To the surprise of many, Margerin [215] constructed Riemannian metrics on the 2-sphere such that the conjugate locus of a point is not closed. Taking the product of such a Riemannian manifold with 2-dimensional Minkowski space gives a globally hyperbolic spacetime in which the caustic of the past light cone of an event is not closed.

In Section 2.8 we gave criteria for the number of past-oriented lightlike geodesics from a point p_O (observation event) to a timelike curve γ_S (worldline of a light source) in an arbitrary spacetime. With Statements (H1), (H2), (H3), and (H4) at hand, the following stronger criteria can be given.

Let (${\mathcal M},g$) be globally hyperbolic, fix a point p_O and an inextendible timelike curve γ_S in ${\mathcal M}$. Then the following is true:

• (H5) Assume that γ_S enters into the chronological past I⁻ (p_O) of p_O. Then there is a past-oriented lightlike geodesic λ from p_O to γ_S that is completely contained in the boundary of I⁻(p_O). This geodesic does not pass through a cut point or through a conjugate point before arriving at γ_S.

• (H6) Assume that γ_S can be reached from po along a past-oriented lightlike geodesic that passes through a conjugate point or through a cut point before arriving at γ_S. Then γ_S can be reached from p_O along a second past-oriented lightlike geodesic.

Statement (H5) was proven in [327] with the help of Morse theory. For a more elementary proof see [268], Proposition 16. Statement (H5) gives a characterization of the primary image in globally hyperbolic spacetimes. (The primary image is the one that shows the light source at an older age than all other images.) The condition of γ_S entering into the chronological past of p_O is necessary to exclude the case that p_O sees no image of γ_S. Statement (H5) implies that there is a unique primary image unless γ_S passes through the cut locus of the past light cone of p_O. The primary image has even parity. If the weak energy condition is satisfied, the focusing theorem implies that the primary image has magnification factor ≥ 1, i.e., that it appears brighter than a source of the same luminosity at the same affine distance and at the same redshift in Minkowski spacetime (recall Sections 2.4 and 2.6, in particular Equation (46)).

For a proof of Statement (H6) see [268], Proposition 17. Statement (H6) says that in a globally hyperbolic spacetime the occurrence of cut points is necessary and sufficient for multiple imaging, and so is the occurrence of conjugate points.

3.2 Wave fronts in globally hyperbolic spacetimes

In Section 2.2 the notion of wave fronts was discussed in an arbitrary spacetime (${\mathcal M},g$). It was mentioned that a wave front can be viewed as a subset of the space ${\mathcal N}$ of all lightlike geodesics in (${\mathcal M},g$). This approach is particularly useful in globally hyperbolic spacetimes, as was demonstrated by Low [209, 210]. The construction is based on the observations that, if (${\mathcal M},g$) is globally hyperbolic and ${\mathcal C}$ is a smooth Cauchy surface, the following is true:

• (N1) ${\mathcal N}$ can be identified with a sphere bundle over ${\mathcal C}$. The identification is made by assigning to each lightlike geodesic its tangent line at the point where it intersects ${\mathcal C}$. As every sphere bundle over an orientable 3-manifold is trivializable, ${\mathcal N}$ is diffeomorphic to ${\mathcal C} \times {S^2}$.

• (N2) ${\mathcal N}$ carries a natural contact structure. (This contact structure is also discussed, in twistor language, in [262], volume II.)

• (N3) The wave fronts are exactly the Legendre submanifolds of ${\mathcal N}$.

Using Statement (N1), the projection from ${\mathcal N}$ to ${\mathcal C}$ assigns to each wave front its intersection with ${\mathcal C}$, i.e., an “instantaneous wave front” or “small wave front” (cf. Section 2.2 for terminology). The points where this projection has non-maximal rank give the caustic of the small wave front. According to the general stability results of Arnold (see [11]), the only caustic points that are stable with respect to local perturbations within the class of Legendre submanifolds are cusps and swallow-tails. By Statement (N3), perturbing within the class of Legendre submanifolds is the same as perturbing within the class of wave fronts. For this local stability result the assumption of global hyperbolicity is irrelevant because every spacelike hypersurface is a Cauchy surface for an appropriately chosen neighborhood of any of its points. So we get the result that was already mentioned in Section 2.2: In an arbitrary spacetime, a caustic point of an instantaneous wave front is stable if and only if it is a cusp or a swallow-tail. Here stability refers to perturbations that keep the metric and the hypersurface fixed and perturb the wave front within the class of wave fronts. For a picture of an instantaneous wave front with cusps and a swallow-tail point, see Figure 28. In Figure 13, the caustic points are neither cusps nor swallow-tails, so the caustic is unstable.

3.3 Fermat’s principle and Morse theory in globally hyperbolic spacetimes

In an arbitrary spacetime, the past-oriented lightlike geodesics from a point p_O (observation event) to a timelike curve γ_S (worldline of light source) are the solutions of a variational principle (Kovner’s version of Fermat’s principle; see Section 2.9). Every solution of this variational principle corresponds to an image on p_O’s sky of γ_S. Determining the number of images is the same as determining the number of solutions to the variational problem. If the variational functional satisfies some technical conditions, the number of solutions to the variational principle can be related to the topology of the space of trial paths. This is the content of Morse theory. In the case at hand, the “technical conditions” turn out to be satisfied in globally hyperbolic spacetimes.

To briefly review Morse theory, we consider a differentiable function $F:{\mathcal X} \rightarrow {\mathbb R}$ on a real manifold ${\mathcal X}$. Points where the differential of F vanishes are called critical points of F. A critical point is called non-degenerate if the Hessian of F is non-degenerate at this point. F is called a Morse function if all its critical points are non-degenerate. In applications to variational problems, ${\mathcal X}$ is the space of trial maps, F is the functional to be varied, and the critical points of F are the solutions to the variational problem. The non-degeneracy condition guarantees that the character of each critical point — local minimum, local maximum, or saddle — is determined by the Hessian of F at this point. The index of the Hessian is called the Morse index of the critical point. It is defined as the maximal dimension of a subspace on which the Hessian is negative definite. At a local minimum the Morse index is zero, at a local maximum it is equal to the dimension of ${\mathcal X}$.

Morse theory was first worked out by Morse [229] for the case that ${\mathcal X}$ is finite-dimensional and compact (see Milnor [224] for a detailed exposition). The main result is the following. On a compact manifold ${\mathcal X}$, for every Morse function the Morse inequalities

$${N_k} \geq {B_k},\quad k = 0,1,2, \ldots,$$

(59)

and the Morse relation

$$\sum\limits_{k = 0}^\infty {{{(- 1)}^k}{N_k} = \sum\limits_{k = 0}^\infty {{{(- 1)}^k}{B_k}}}$$

(60)

hold true. Here N_k denotes the number of critical points with Morse index k and B_k denotes the kth Betti number of ${\mathcal X}$. Formally, B_k is defined for each topological space ${\mathcal X}$ in terms of the kth singular homology space ${H_k}({\mathcal X})$ with coefficients in a field ${\mathbb F}$ (see, e.g., [78], p. 32). (The results of Morse theory hold for any choice of ${\mathbb F}$.) Geometrically, B₀ counts the connected components of ${\mathcal X}$ and, for k ≥ 1, B_k counts the “holes” in ${\mathcal X}$ that prevent a k-cycle with coefficients in ${\mathbb F}$ from being a boundary. In particular, if ${\mathcal X}$ is contractible to a point, then B_k = 0 for k ≥ 1. The right-hand side of Equation (60) is, by definition, the Euler characteristic of ${\mathcal X}$. By compactness of ${\mathcal X}$, all N_kand B_k are finite and in both sums of Equation (60) only finitely many summands are different from zero.

Palais and Smale [251, 252] realized that the Morse inequalities and the Morse relations are also true for a Morse function F on a non-compact and possibly infinite-dimensional Hilbert manifold, provided that F is bounded below and satisfies a technical condition known as Condition C or Palais-Smale condition. In that case, the N_k and B_k need not be finite.

The standard application of Morse theory is the geodesic problem for Riemannian (i.e., positive definite) metrics: given two points in a Riemannian manifold, to find the geodesics that join them. In this case F is the “energy functional” (squared-length functional). Varying the energy functional is related to varying the length functional like Hamilton’s principle is related to Maupertuis’ principle in classical mechanics. For the space ${\mathcal X}$ one chooses, in the Palais-Smale approach [251], the H¹-curves between the given two points. (An Hⁿ-curve is a curve with locally square-integrable nth derivative). This is an infinite-dimensional Hilbert manifold. It has the same homotopy type (and thus the same Betti numbers) as the loop space of the Riemannian manifold. (The loop space of a connected topological space is the space of all continuous curves joining any two fixed points.) On this Hilbert manifold, the energy functional is always bounded from below, and its critical points are exactly the geodesics between the given end-points. A critical point (geodesic) is non-degenerate if the two end-points are not conjugate to each other, and its Morse index is the number of conjugate points in the interior, counted with multiplicity (“Morse index theorem”). The Palais-Smale condition is satisfied if the Riemannian manifold is complete. So one has the following result: Fix any two points in a complete Riemannian manifold that are not conjugate to each other along any geodesic. Then the Morse inequalities (59) and the Morse relation (60) are true, with N_k denoting the number of geodesics with Morse index k between the two points and B_k denoting the kth Betti number of the loop space of the Riemannian manifold. The same result is achieved in the original version of Morse theory [229] (cf. [224]) by choosing for ${\mathcal X}$ the space of broken geodesics between the two given points, with N break points, and sending N → ∞ at the end.

Using this standard example of Morse theory as a pattern, one can prove an analogous result for Kovner’s version of Fermat’s principle. The following hypotheses have to be satisfied:

• (M1) p_O is a point and γ_S is a timelike curve in a globally hyperbolic spacetime (${\mathcal M},g$).

• (M2) γ_S does not meet the caustic of the past light cone of p_O.

• (M3) Every continuous curve from p_O to γ_S can be continuously deformed into a past-oriented lightlike curve, with all intermediary curves starting at p_O and terminating on γ_S.

The global hyperbolicity assumption in Statement (M1) is analogous to the completeness assumption in the Riemannian case. Statement (M2) is the direct analogue of the non-conjugacy condition in the Riemmanian case. Statement (M3) is necessary for relating the space of trial paths (i.e., of past-oriented lightlike curves from p_O to γ_S) to the loop space of the spacetime manifold or, equivalently, to the loop space of a Cauchy surface. If Statements (M1), (M2), and (M3) are valid, the Morse inequalities (59) and the Morse relation (60) are true, with N_k denoting the number of past-oriented lightlike geodesics from p_O to γ_S that have k conjugate points in its interior, counted with muliplicity, and B_k denoting the kth Betti number of the loop space of ${\mathcal M}$ or, equivalently, of a Cauchy surface. This result was proven by Uhlenbeck [327] à la Morse and Milnor, and by Giannoni and Masiello [136] in an infinite-dimensional Hilbert manifold setting à la Palais and Smale. A more general version, applying to spacetime regions with boundaries, was worked out by Giannoni, Masiello, and Piccione [137, 138]. In the work of Giannoni et al., the proofs are given in greater detail than in the work of Uhlenbeck.

If Statements (M1), (M2), and (M3) are satisfied, Morse theory gives us the following results about the number of images of γ_S on the sky of p_O (cf. [220]):

• (R1) If ${\mathcal M}$ is not contractible to a point, there are infinitely many images. This follows from Equation (59) because for the loop space of a non-contractible space either B₀ is infinite or almost all B_k are different from zero [304].

• (R2) If ${\mathcal M}$ is contractible to a point, the total number of images is infinite or odd. This follows from Equation (60) because in this case the loop space of ${\mathcal M}$ is contractible to a point, so all Betti numbers B_k vanish with the exception of B₀ = 1. As a consequence, Equation (60) can be written as N₊ − N₋ = 1, where N₊ is the number of images with even parity (geodesics with even Morse index) and N₋ is the number of images with odd parity (geodesics with odd Morse index), hence N₊ + N₋ = 2N₋ + 1.

These results apply, in particular, to the following situations of physical interest:

3.3.1 Black hole spacetimes

Let (${\mathcal M},g$) be the domain of outer communication of the Kerr spacetime, i.e., the region between the (outer) horizon and infinity (see Section 5.8). Then the assumption of global hyperbolicity is satisfied and ${\mathcal M}$ is not contractible to a point. Statement (M3) is satisfied if γ_S is inextendible and approaches neither the horizon nor (past lightlike) infinity for t → −∞. (This can be checked with the help of an analytical criterion that is called the “metric growth condition” in [327].) If, in addition Statement (M2) is satisfied, the reasoning of Statement (R1) applies. Hence, a Kerr black hole produces infinitely many images. The same argument can be applied to black holes with (electric, magnetic, Yang-Mills, …) charge.

3.3.2 Asymptotically simple and empty spacetimes

As discussed in Section 3.4, asymptotically simple and empty spacetimes are globally hyperbolic and contractible to a point. They can be viewed as models of isolated transparent gravitational lenses. Statement (M3) is satisfied if γ_S is inextendible and bounded away from past lightlike infinity ℐ^-. If, in addition, Statement (M2) is satisfied, Statement (R2) guarantees that the number of images is infinite or odd. If it were infinite, we had as the limit curve a past-inextendible lightlike geodesic that would not go out to ℐ^-, in contradiction to the definition of asymptotic simplicity. So the number of images must be finite and odd. The same odd-number theorem can also be proven with other methods (see Section 3.4).

In this way Morse theory provides us with precise mathematical versions of the statements “A black hole produces infinitely many images” and “An isolated transparent gravitational lens produces an odd number of images”. When comparing this theoretical result with observations one has to be aware of the fact that some images might be hidden behind the deflecting mass, some might be too faint for being detected, and some might be too close together for being resolved.

In conformally stationary spacetimes, with γ_S being an integral curve of the conformal Killing vector field, a simpler version of Fermat’s principle and Morse theory can be used (see Section 4.2).

3.4 Lensing in asymptotically simple and empty spacetimes

In elementary optics one often considers “light sources at infinity” which are characterized by the fact that all light rays emitted from such a source are parallel to each other. In general relativity, “light sources at infinity” can be defined if one restricts to a special class of spacetimes. These spacetimes, known as “asymptotically simple and empty” are, in particular, globally hyperbolic. Their formal definition, which is due to Penrose [258], reads as follows (cf. [154], p. 222., and [117], Section 2.3). (Recall that a spacetime is called “strongly causal” if each neighborhood of an event p admits a smaller neighborhood that is intersected by any non-spacelike curve at most once.)

A spacetime (${\mathcal M},g$) is called asymptotically simple and empty if there is a strongly causal spacetime ($\tilde {\mathcal M},\tilde g$) with the following properties:

• (S1) ${\mathcal M}$ is an open submanifold of ${\tilde {\mathcal M}}$ with a non-empty boundary $\partial {\mathcal M}$.

• (S2) There is a smooth function $\Omega:\tilde {\mathcal M} \rightarrow {\mathbb R}$ such that ${\mathcal M} = \{p \in \tilde {\mathcal M}\vert \Omega (p) > 0\}, \partial {\mathcal M} = \{p \in \tilde {\mathcal M}\vert \Omega (p) = 0\}$, dΩ ≠ 0 everywhere on $\partial {\mathcal M}$ and $\tilde g = {\Omega ^2}g$ on ${\mathcal M}$.

• (S3) Every inextendible lightlike geodesic in M has past and future end-point on $\partial {\mathcal M}$.

• (S4) There is a neighborhood ${\mathcal V}$ of $\partial {\mathcal M}$ such that the Ricci tensor of g vanishes on ${\mathcal V} \cap {\mathcal M}$.

Asymptotically simple and empty spacetimes are mathematical models of transparent uncharged gravitating bodies that are isolated from all other gravitational sources. In view of lensing, the transparency condition (S3) is particularly important.

We now summarize some well-known facts about asymptotically simple and empty spacetimes (cf. again [154], p. 222, and [117], Section 2.3). Every asymptotically simple and empty spacetime is globally hyperbolic. $\partial {\mathcal M}$ is a ${\tilde g}$-lightlike hypersurface of ${\tilde {\mathcal M}}$. It has two connected components, denoted ℐ⁺ and ℐ^-. Each lightlike geodesic in (${\mathcal M},g$) has past end-point on ℐ^- and future end-point on ℐ₊roch [134] gave a proof that every Cauchy surface ${\mathcal C}$ of an asymptotically simple and empty spacetime has topology ℝ³ and that ℐ_± has topology S² × ℝ. The original proof, which is repeated in [154], is incomplete. A complete proof that ${\mathcal C}$ must be contractible and that ℐ_± has topology S² × ℝ was given by Newman and Clarke [238] (cf. [237]); the stronger statement that C must have topology ℝ³ needs the assumption that the Poincaré conjecture is true (i.e., that every compact and simply connected 3-manifold is a 3-sphere). In [238] the authors believed that the Poincaré conjecture was proven, but the proof they are refering to was actually based on an error. If the most recent proof of the Poincaré conjecture by Perelman [263] (cf. [346]) turns out to be correct, this settles the matter.

As ℐ_± is a lightlike hypersurface in ${\tilde {\mathcal M}}$, it is in particular a wave front in the sense of Section 2.2. The generators of ℐ_± are the integral curves of the gradient of Ω. The generators of ℐ_- can be interpreted as the “worldlines” of light sources at infinity that send light into ${\mathcal M}$. The generators of ℐ₊ can be interpreted as the “worldlines” of observers at infinity that receive light from ${\mathcal M}$. This interpretation is justified by the observation that each generator of ℐ_± is the limit curve for a sequence of timelike curves in ${\mathcal M}$.

For an observation event p_O inside ${\mathcal M}$ and light sources at infinity, lensing can be investigated in terms of the exact lens map (recall Section 2.1), with the role of the source surface ${\mathcal T}$ played by ℐ_-. (For the mathematical properties of the lens map it is rather irrelevant whether the source surface is timelike, lightlike or even spacelike. What matters is that the arriving light rays meet the source surface transversely.) In this case the lens map is a map S² → S², namely from the celestial sphere of the observer to the set of all generators of ℐ_-. One can construct it in two steps: First determine the intersection of the past light cone of p_O with ℐ_-, then project along the generators. The intersections of light cones with ℐ_± (“light cone cuts of null infinity”) have been studied in [189, 188].

One can assign a mapping degree (= Brouwer degree = winding number) to the lens map S² → S² and prove that it must be ±1 [270]. (The proof is based on ideas of [238, 237]. Earlier proofs of similar statements — [188], Lemma 1, and [268], Theorem 6 — are incorrect, as outlined in [270].) Based on this result, the following odd-number theorem can be proven for observer and light source inside ${\mathcal M}$ [270]: Fix a point p_O and a timelike curve γ_S in an asymptotically simple and empty spacetime (${\mathcal M},g$). Assume that the image of γ_S is a closed subset of ℐ₊ and that γ_S meets neither the point p_O nor the caustic of the past light cone of p_O. Then the number of past-pointing lightlike geodesics from p_O to γ_S in ${\mathcal M}$ is finite and odd. The same result can be proven with the help of Morse theory (see Section 3.3).

We will now give an argument to the effect that in an asymptotically simple and empty spacetime the non-occurrence of multiple imaging is rather exceptional. The argument starts from a standard result that is used in the Penrose-Hawking singularity theorems. This standard result, given as Proposition 4.4.5 in [154], says that along a lightlike geodesic that starts at a point p_O there must be a point conjugate to p_O, provided that

• 1. the so-called generic condition is satisfied at p_O,

• 2. the weak energy condition is satisfied along the geodesic, and

• 3. the geodesic can be extended sufficiently far.

The last assumption is certainly true in an asymptotically simple and empty spacetime because there all lightlike geodesics are complete. Hence, the generic condition and the weak energy condition guarantee that every past light cone must have a caustic point. We know from Section 3.1 that this implies multiple imaging for every observer. In other words, the only asymptotically simple and empty spacetimes in which multiple imaging does not occur are non-generic cases (like Minkowski spacetime) and cases where the gravitating bodies have negative energy.

The result that, under the aforementioned conditions, light cones in an asymptotically simple and empty spacetime must have caustic points is due to [165]. This paper investigates the past light cones of points on ℐ₊ and their caustics. These light cones are the generalizations, to an arbitrary asymptotically simple and empty spacetime, of the lightlike hyperplanes in Minkowski spacetime. With their help, the eikonal equation (Hamilton-Jacobi equation) g^ij∂_iS∂_jS = 0 in an asymptotically simple and empty spacetime can be studied in analogy to Minkowski spacetime [126, 125]. In Minkowski spacetime the lightlike hyperplanes are associated with a two-parameter family of solutions to the eikonal equation. In the terminology of classical mechanics such a family is called a complete integral. Knowing a complete integral allows constructing all solutions to the Hamilton-Jacobi equation. In an asymptotically simple and empty spacetime the past light cones of points on ℐ₊ give us, again, a complete integral for the eikonal equation, but now in a generalized sense, allowing for caustics. These past light cones are wave fronts, in the sense of Section 2.2, and cannot be represented as surfaces S = constant near caustic points. The way in which all other wave fronts can be determined from knowledge of this distinguished family of wave fronts is detailed in [125]. The distinguished family of wave fronts gives a natural choice for the space of trial maps in the Frittelli-Newman variational principle which was discussed in Section 2.9.

4 Lensing in Spacetimes with Symmetry

4.1 Lensing in conformally flat spacetimes

By definition, a spacetime is conformally flat if the conformal curvature tensor (=Weyl tensor) vanishes. An equivalent condition is that every point admits a neighborhood that is conformal to an open subset of Minkowski spacetime. As a consequence, conformally flat spacetimes have the same local conformal symmetry as Minkowski spacetime, that is they admit 15 independent conformal Killing vector fields. The global topology, however, may be different from the topology of Minkowski spacetime. The class of conformally flat spacetimes includes all (kinematic) Robertson-Walker spacetimes. Other physically interesting examples are some (generalized) interior Schwarzschild solutions and some pure radiation spacetimes. All conformally flat solutions to Einstein’s field equation with a perfect fluid or an electromagnetic field are known (see [311], Section 37.5.3).

If a spacetime is globally conformal to an open subset of Minkowski spacetime, the past light cone of every event is an embedded submanifold. Hence, multiple imaging cannot occur (recall Section 2.8). For instance, multiple imaging occurs in spatially closed but not in spatially open Robertson-Walker spacetimes. In any conformally flat spacetime, there is no image distortion, i.e., a sufficiently small sphere always shows a circular outline on the observer’s sky (recall Section 2.5). Correspondingly, every infinitesimally thin bundle of light rays with a vertex is circular, i.e., the extremal angular diameter distances D₊ and D₋ coincide (recall Section 2.4). In addition, D₊ = D₋ also coincides with the area distance D_area, at least up to sign. D₊ = D₋ changes sign at every caustic point. As D₊ has a zero if and only if D₋ has a zero, all caustic points of an infinitesimally thin bundle with vertex are of multiplicity two (anastigmatic focusing), so all images have even parity.

The geometry of light bundles can be studied directly in terms of the Jacobi equation (= equation of geodesic deviation) along lightlike geodesics. For a detailed investigation of the latter in conformally flat spacetimes, see [273]. The more special case of Friedmann-Lemaître-Robertson-Walker spacetimes (with dust, radiation, and cosmological constant) is treated in [101]. For bundles with vertex, one is left with one scalar equation for D₊ = D₋ = ±D_area, that is the focusing equation (44) with σ = 0. This equation can be explicitly integrated for Friedmann-Robertson-Walker spacetimes (dust without cosmological constant). In this way one gets, for the standard observer field in such a spacetime, relations between redshift and (area or luminosity) distance in closed form [219]. There are generalizations for a Robertson-Walker universe with dust plus cosmological constant [178] and dust plus radiation plus cosmological constant [71]. Similar formulas can be written for the relation between age and redshift [322].

4.2 Lensing in conformally stationary spacetimes

Conformally stationary spacetimes are models for gravitational fields that are time-independent up to an overall conformal factor. (The time-dependence of the conformal factor is important, e.g., if cosmic expansion is to be taken into account.) This is a reasonable model assumption for many, though not all, lensing situations of interest. It allows describing light rays in a 3-dimensional (spatial) formalism that will be outlined in this section. The class of conformally stationary spacetimes includes spherically symmetric and static spacetimes (see Sections 4.3) and axisymmetric stationary spacetimes (see Section 4.4). Also, conformally flat spacetimes (see Section 4.1) are conformally stationary, at least locally. A physically relevant example where the conformal-stationarity assumption is not satisfied is lensing by a gravitational wave (see Section 5.11).

By definition, a spacetime is conformally stationary if it admits a timelike conformal Killing vector field W. If W is complete and if there are no closed timelike curves, the spacetime must be a product, ${\mathcal M} \simeq {\mathbb R} \times \hat {\mathcal M}$ with a (Hausdorff and paracompact) 3-manifold $\hat{\mathcal M}$ and W parallel to the ℝ-lines [148]. If we denote the projection from ${\mathcal M}$ to ℝ by t and choose local coordinates x = (x¹, x², x³) on $\hat{\mathcal M}$, the metric takes the form

$$g = {e^{2f(t,x)}}\left({- {{(dt + {{\hat \phi}_\mu}(x)d{x^\mu})}^2} + {{\hat g}_{\mu \nu}}(x)d{x^\mu}d{x^\nu}} \right)$$

(61)

with μ, ν, … = 1, 2, 3. The conformal factor e^2f does not affect the lightlike geodesics apart from their parametrization. So the paths of light rays are completely determined by the metric $\hat g = {{\hat g}_{\mu \nu}}(x)d{x^\mu}d{x^\nu}$ and the one-form $\hat \phi = {{\hat \phi}_\mu}(x)d{x^\mu}$ which live on $\hat{\mathcal M}$. The metric ${\hat g}$ must be positive definite to give a spacetime metric of Lorentzian signature. We call f the redshift potential, ${\hat g}$ the Fermat metric and ${\hat \phi}$ the Fermat one-form. The motivation for these names will become clear from the discussion below.

If ${{\hat \phi}_\mu} = {\partial _\mu}h$, where h is a function of x = (x¹, x², x³), we can change the time coordinate according to t ↦ t + h(x), thereby transforming ${{\hat \phi}_\mu}d{x^\mu}$ to zero, i.e., making the surfaces t = constant orthogonal to the t-lines. This is the conformally static case. Also, Equation (61) includes the stationary case (f independent of t) and the static case (${{\hat \phi}_\mu} = {\partial _\mu}h$ and f independent of t).

In Section 2.9 we have discussed Kovner’s version of Fermat’s principle which characterizes the lightlike geodesics between a point (observation event) p_O and a timelike curve (worldline of light source) γ_S. In a conformally stationary spacetime we may specialize to the case that γ_S is an integral curve of the conformal Killing vector field, parametrized by the “conformal time” coordinate t (in the past-pointing sense, to be in agreement with Section 2.9). Without loss of generality, we may assume that the observation event p_O takes place at t = 0. Then for each trial path (past-oriented lightlike curve) λ from p_O to γ_S the arrival time is equal to the travel time in terms of the time function t. By Equation (61) this puts the arrival time functional into the following coordinate form

$$T(\lambda) = \int\nolimits_{{\ell _1}}^{{\ell _2}} {\left({\sqrt {{{\hat g}_{\mu \nu}}(x){{d{x^\mu}} \over {d\ell}}{{d{x^\nu}} \over {d\ell}}} - {{\hat \phi}_\mu}(x){{d{x^\mu}} \over {d\ell}}} \right)} d\ell,$$

(62)

where ℓ is any parameter along the trial path, ranging over an interval [ℓ₁, ℓ₂] that depends on the individual curve. The right-hand side of Equation (62) is a functional for curves in $\hat{\mathcal M}$ with fixed end-points. The projections to $\hat{\mathcal M}$ of light rays are the stationary points of this functional. In general, the right-hand side of Equation (62) is the length functional of a Finsler metric. In the conformally static case ${{\hat \phi}_\mu} = {\partial _\mu}h$, the integral over ${{\hat \phi}_\mu}(x)d{x^\mu}/d\ell$ is the same for all trial paths, so we are left with the length functional of the Fermat metric ${\hat g}$. In this case the light rays, if projected to $\hat{\mathcal M}$, are the geodesics of ${\hat g}$. Note that the travel time functional (62) is invariant under reparametrization; in the terminology of classical mechanics, it is a special case of Maupertuis’ principle. It is often convenient to switch to a parametrization-dependent variational principle which, in the terminology of classical mechanics, is called Hamilton’s principle. The Maupertuis principle with action functional (62) corresponds to Hamilton’s principle with a Lagrangian

$${\mathcal L} = {1 \over 2}{\hat g_{\mu \nu}}(x){{d{x^\mu}} \over {d\ell}}{{d{x^\nu}} \over {d\ell}} - {\hat \phi _\mu}{{d{x^\mu}} \over \ell},$$

(63)

(see, e.g., Carathéodory [52], Sections 304–307). The pertaining Euler-Lagrange equations read

$${\hat g_{\mu \nu}}\left({{{{d^2}{x^\nu}} \over {d{\ell ^2}}} + \hat \Gamma _{\sigma \tau}^\nu {{d{x^\sigma}} \over {d\ell}}{{d{x^\tau}} \over {d\ell}}} \right) = \left({{\partial _\nu}{{\hat \phi}_\mu} - {\partial _\mu}{{\hat \phi}_\nu}} \right){{d{x^\mu}} \over {d\ell}}$$

(64)

where $\hat \Gamma _{\sigma \tau}^\nu$ are the Christoffel symbols of the Fermat metric ${\hat g}$. The solutions admit the constant of motion

$${\hat g_{\mu \nu}}(x){{d{x^\mu}} \over {d\ell}}{{d{x^\nu}} \over {d\ell}} = {\rm{constant,}}$$

(65)

which can be chosen equal to 1 for each ray, such that ℓ gives the ${\hat g}$-arclength. By Equation (62), the latter gives the travel time if $\hat \phi = 0$. According to Equation (64), the Fermat two-form

$${\hat \omega} = d\hat \phi$$

(66)

exerts a kind of Coriolis force on the light rays. This force has the same mathematical structure as the Lorentz force in a magnetostatic field. In this analogy, $\hat \phi = 0$ corresponds to the magnetic (vector) potential. In other words, light rays in a conformally stationary spacetime behave like charged particles, with fixed charge-to-mass ratio, in a magnetostatic field ${\hat w}$ on a Riemannian manifold ($\hat M,\hat g$).

Fermat’s principle in static spacetimes dates back to Weyl [347] (cf. [206, 319]). The stationary case was treated by Pham Mau Quan [284], who even took an isotropic medium into account, and later, in a more elegant presentation, by Brill [42]. These versions of Fermat’s principle are discussed in several text-books on general relativity (see, e.g., [225, 116, 312] for the static and [200] for the stationary case). A detailed discussion of the conformally stationary case can be found in [265]. Fermat’s principle in conformally stationary spacetimes was used as the starting point for deriving the lens equation of the quasi-Newtonian apporoximation formalism by Schneider [297] (cf. [299]). As an alternative to the name “Fermat metric” (used, e.g., in [116, 312, 265]), the names “optical metric” (see, e.g., [141, 79]) and “optical reference geometry” (see, e.g., [4]) are also used.

In the conformally static case, one can apply the standard Morse theory for Riemannian geodesics to the Fermat metric ${\hat g}$ to get results on the number of ${\hat g}$-geodesics joining two points in space. This immediately gives results on the number of lightlike geodesics joining a point in spacetime to an integral curve of W = ∂_t. Completeness of the Fermat metric corresponds to global hyperbolicity of the spacetime metric. The relevant techniques, and their generalization to (conformally) stationary spacetimes, are detailed in a book by Masiello [218]. (Note that, in contrast to standard terminology, Masiello’s definition of a stationary spacetime includes the assumption that the hypersurfaces t = constant are spacelike.) The resulting Morse theory is a special case of the Morse theory for Fermat’s principle in globally hyperbolic spacetimes (see Section 3.3). In addition to Morse theory, other standard methods from Riemannian geometry have been applied to the Fermat metric, e.g., convexity techniques [139, 140].

If the metric (61) is conformally static, ${{\hat \phi}_\mu}(x) = {\partial _\mu}h(x)$, and if the Fermat metric is conformal to the Euclidean metric, ${{\hat g}_{\mu \nu}}(x) = n{(x)^2}{\delta _{\mu \nu}}$, the arrival time functional (62) can be written as

$$T(\lambda) = \int\nolimits_{{\ell _1} = 0}^{{\ell _2}} {n(x)d\ell} + {\rm{constant}},$$

(67)

where ℓ is Euclidean arclength. Hence, Fermat’s principle reduces to its standard optics form for an isotropic medium with index of refraction n on Euclidean space. As a consequence, light propagation in a spacetime with the assumed properties can be mimicked by a medium with an appropriately chosen index of refraction. This remark applies, e.g., to spherically symmetric and static spacetimes (see Section 4.3) and, in particular, to the Schwarzschild spacetime (see Section 5.1). The analogy with ordinary optics in media has been used for constructing, in the laboratory, analogue models for light propagation in general-relativistic spacetimes (see [242]).

Extremizing the functional (67) is formally analogous to Maupertuis’ principle for a particle in a scalar potential on flat space, which is discussed in any book on classical mechanics. Dropping the assumption that the Fermat one-form is a differential, but still requiring the Fermat metric to be conformal to the Euclidean metric, corresponds to introducing an additional vector potential. This form of the optical-mechanical analogy, for light rays in stationary spacetimes whose Fermat metric is conformal to the Euclidean metric, is discussed, e.g., in [7].

The conformal factor e^2f in Equation (61) does not affect the paths of light rays. However, it does affect redshifts and distance measures (recall Section 2.4). If g is of the form (61), for every lightlike geodesic λ the quantity $g(\dot \lambda, {\partial _t})$ is a constant of motion. This leads to a particularly simple form of the general redshift formula (36). We consider an arbitrary lightlike geodesic s ↦ λ(s) in terms of its coordinate representation s ↦ (t(s), x¹(s), x²(s), x³(s)). If both observer and emitter are at rest in the sense that their 4-velocities U_O and U_S are parallel to W = ∂_t, Equation (36) can be rewritten as

$$\log (1 + z(s)) = f(t(s),x(s)) - f(t(0),x(0)).$$

(68)

This justifies calling f the redshift potential. It is shown in [151] that there is a redshift potential for a congruence of timelike curves in a spacetime if and only if the timelike curves are the integral curves of a conformal Killing vector field. The notion of a redshift potential or redshift function is also discussed in [74]. Note that Equation (68) immediately determines the redshift in conformally stationary spacetimes for any pair of observer and emitter. If the -velocity of the observer or of the emitter is not parallel to W = ∂_t, one just has to add the usual special-relativistic Doppler factor.

Conformally stationary spacetimes can be characterized by another interesting property. Let W be a timelike vector field in a spacetime and fix three observers whose worldlines are integral curves of W. Then the angle under which two of them are seen by the third one remains constant in the course of time, for any choice of the observers, if and only if W is proportional to a conformal Killing vector field. For a proof see [151].

4.3 Lensing in spherically symmetric and static spacetimes

The class of spherically symmetric and static spacetimes is of particular relevance in view of lensing, because it includes models for non-rotating stars and black holes (see Sections 5.1, 5.2, 5.3), but also for more exotic objects such as wormholes (see Section 5.4), monopoles (see Section 5.5), naked singularities (see Section 5.6), and Boson or Fermion stars (see Section 5.7). Here we collect the relevant formulas for an unspecified spherically symmetric and static metric. We find it convenient to write the metric in the form

$$g = {e^{2f(r)}}(- d{t^2} + S{(r)^2}d{r^2} + R{(r)^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\varphi ^2})).$$

(69)

As Equation (69) is a special case of Equation (61), all results of Section 4.2 for conformally stationary metrics apply. However, much stronger results are possible because for metrics of the form (69) the geodesic equation is completely integrable. Hence, all relevant quantities can be determined explicitly in terms of integrals over the metric coefficients.

4.3.1 Redshift and Fermat geometry

Comparison of Equation (69) with the general form (61) of a conformally stationary spacetime shows that here the redshift potential f is a function of r only, the Fermat one-form ${\hat \phi}$ vanishes, and the Fermat metric ${\hat g}$ is of the special form

$$\hat g = S{(r)^2}d{r^2} + R{(r)^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\varphi ^2}).$$

(70)

By Fermat’s principle, the geodesics of ${\hat g}$ coincide with the projection to 3-space of light rays. The travel time (in terms of the time coordinate t) of a lightlike curve coincides with the ${\hat g}$-arclength of its projection. By symmetry, every ${\hat g}$-geodesic stays in a plane through the origin. From Equation (70) we read that the sphere of radius r has area 4πR(r)² with respect to the Fermat metric. Also, Equation (70) implies that the second fundamental form of this sphere is a multiple of its first fundamental form, with a factor −R′(r) (R(r) S(r))⁻¹. If

$${R{\prime}}({r_{\rm{p}}}) = 0,$$

(71)

the sphere r = r_p is totally geodesic, i.e., a ${\hat g}$-geodesic that starts tangent to this sphere remains in it. The best known example for such a light sphere or photon sphere is the sphere r = 3m in the Schwarzschild spacetime (see Section 5.1). Light spheres also occur in the spacetimes of wormholes (see Section 5.4). If R″(r_p) < 0, the circular light rays in a light sphere are stable with respect to radial perturbations, and if R″(r_p) < 0, they are unstable like in the Schwarschild case. The condition under which a spherically symmetric static spacetime admits a light sphere was first given by Atkinson [13]. Abramowicz [1] has shown that for an observer traveling along a circular light orbit (with subluminal velocity) there is no centrifugal force and no gyroscopic precession. Claudel, Virbhadra, and Ellis [59] investigated, with the help of Einstein’s field equation and energy conditions, the amount of matter surrounded by a light sphere. Among other things, they found an energy condition under which a spherically symmetric static black hole must be surrounded by a light sphere. A purely kinematical argument shows that any spherically symmetric and static spacetime that has a horizon at r = r_H and is asymptotically flat for r → ∞ must contain a light sphere at some radius between r_H and ∞ (see Hasse and Perlick [153]). In the same article, it is shown that in any spherically symmetric static spacetime with a light sphere there is gravitational lensing with infinitely many images. Bozza [37] investigated a strong-field limit of lensing in spherically symmetric static spacetimes, as opposed to the well-known weak-field limit, which applies to light rays that come close to an unstable light sphere. (Actually, the term “strong-bending limit” would be more appropriate because the gravitational field, measured in terms of tidal forces, need not be particularly strong near an unstable light sphere.) This limit applies, in particular, to light rays that approach the sphere r = 3m in the Schwarzschild spacetime (see [39] and, for illustrations, Figures 15, 16, and 17).

4.3.2 Index of refraction and embedding diagrams

Transformation to an isotropic radius coordinate ${\tilde r}$ via

$${{S(r)dr} \over {R(r)}} = {{d\tilde r} \over {\tilde r}}$$

(72)

takes the Fermat metric (70) to the form

$$\hat g = n{(\tilde r)^2}(d{\tilde r^2} + {\tilde r^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\varphi ^2}))$$

(73)

where

$$n(\tilde r) = {{R(r)} \over {\tilde r}}.$$

(74)

On the right-hand side r has to be expressed by ${\tilde r}$ with the help of Equation (72). The results of Section 4.2 imply that the lightlike geodesics in a spherically symmetric static spacetime are equivalent to the light rays in a medium with index of refraction (74) on Euclidean 3-space. For arbitrary metrics of the form (69), this result is due to Atkinson [13]. It reduces the lightlike geodesic problem in a spherically symmetric static spacetime to a standard problem in ordinary optics, as treated, e.g., in [212], §27, and [199], Section 4. One can combine this result with our earlier observation that the integral in Equation (67) has the same form as the functional in Maupertuis’ principle in classical mechanics. This demonstrates that light rays in spherically symmetric and static spacetimes behave like particles in a spherically symmetric potential on Euclidean 3-space (cf., e.g., [105]). If the embeddability condition

$$S{(r)^2} \geq R{\prime}{(r)^2}$$

(75)

is satisfied, we define a function Z(r) by

$$Z{\prime}(r) = \sqrt {S{{(r)}^2} - {R{\prime}}{{(r)}^2}.}$$

(76)

then the Fermat metric (70) reads

$$\hat g = {(dR(r))^2} + R{(r)^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\varphi ^2}) + dZ{(r)^2}.$$

(77)

If restricted to the equatorial plane ϑ = π/2, the metric (77) describes a surface of revolution, embedded into Euclidean 3-space as

$$(r,\varphi) \mapsto (R(r)\cos \varphi, Z(r)).$$

(78)

Such embeddings of the Fermat geometry have been visualized for several spacetimes of interest (see Figure 11 for the Schwarzschild case and [160] for other examples). This is quite instructive because from a picture of a surface of revolution one can read the qualitative features of its geodesics without calculating them. Note that Equation (72) defines the isotropic radius coordinate uniquely up to a multiplicative constant. Hence, the straight lines in this coordinate representation give us an unambiguously defined reference grid for every spherically symmetric and static spacetime. These straight lines have been called triangulation lines in [62, 63], where their use for calculating bending angles, exactly or approximately, is outlined.

4.3.3 Light cone

In a spherically symmetric static spacetime, the (past) light cone of an event p_O can be written in terms of integrals over the metric coefficients. We first restrict to the equatorial plane ϑ = π/2. The ${\hat g}$-geodesics are then determined by the Lagrangian

$$L = {1 \over 2}\left({S{{(r)}^2}{{\left({{{dr} \over {d\ell}}} \right)}^2} + R{{(r)}^2}{{\left({{{d\varphi} \over {d\ell}}} \right)}^2}} \right).$$

(79)

For fixed radius value r_O, initial conditions

$$\begin{array}{*{20}c}{r(0) = {r_{\rm{O}}},} & {{{dr} \over {d\ell}}(0) = {{\cos \Theta} \over {S({r_{\rm{O}}})}},} \\ {\varphi (0) = 0,} & {{{d\varphi} \over {d\ell}}(0) = {{\sin \Theta} \over {R({r_{\rm{O}}})}},} \\ \end{array}$$

(80)

determine a unique solution r = r(ℓ, Θ), ϕ = φ(ℓ, Θ) of the Euler-Lagrange equations. Θ measures the initial direction with respect to the symmetry axis (see Figure 6). We get all light rays issuing from the event r = r_O, ϕ = 0, ϑ = π/2, t = t_O into the past by letting Θ range from 0 to π and applying rotations around the symmetry axis. This gives us the past light cone of this event in the form

$$(\ell ,\Psi ,\Theta) \mapsto \left({\begin{array}{*{20}c}{{t_{\rm{O}}} - \ell} \\ {{\rm{r}}(\ell ,\Theta)\,{\rm{sin}}\,\phi (\ell ,\Theta)\cos \Psi} \\ {{\rm{r}}(\ell ,\Theta)\sin \phi (\ell ,\Theta)\sin \Psi} \\ {{\rm{r}}(\ell ,\Theta)\,\cos \phi (\ell ,\Theta)} \\ \end{array}} \right).$$

(81)

Ψ and Θ are spherical coordinates on the observer’s sky. If we let t_O float over ℝ, we get the observational coordinates (4) for an observer on a t-line, up to two modifications. First, t_O is not the same as proper time τ; however, they are related just by a constant,

$${{d\tau} \over {d{t_{\rm{O}}}}} = {e^{- f({r_{\rm{O}}})}}.$$

(82)

Second, i is not the same as the affine parameter s; along a ray with initial direction Θ, they are related by

$${{ds} \over {d\ell}} = {e^{- f(r(\ell, \Theta))}}.$$

(83)

The constants of motion

$$R{(r)^2}{{d\varphi} \over {d\ell}} = R({r_{\rm{O}}})\sin \Theta, \quad \quad S{(r)^2}{\left({{{dr} \over {{d_\ell}}}} \right)^2} + R{(r)^2}{\left({{{d\varphi} \over {d\ell}}} \right)^2} = 1$$

(84)

give us the functions r(ℓ, Θ), φ(ℓ, Θ) in terms of integrals,

$$\ell = \int\nolimits_{{r_{\rm{O}}} \ldots}^{\ldots {\rm{r(}}\ell, \Theta)} {{{R(r)S(r)dr} \over {\sqrt {R{{(r)}^2} - R{{({r_{\rm{O}}})}^2}{{\sin}^2}\Theta}}}},$$

(85)

$$\phi (\ell, \Theta) = R({r_{\rm{O}}})\sin \Theta \int\nolimits_{{r_{\rm{O}}} \ldots}^{\ldots {\rm{r(}}\ell, \Theta)} {{{S(r)dr} \over {R(r)\sqrt {R{{(r)}^2} - R{{({r_{\rm{O}}})}^2}{{\sin}^2}\Theta}}}},$$

(86)

Here the notation with the dots is a short-hand; it means that the integral is to be decomposed into sections where r(ℓ, Θ) is a monotonous function of ℓ and that the absolute value of the integrals over all sections have to be added up. Turning points occur at radius values where R(r) = R(r_O) sin Θ and R′(r) ≠ 0 (see Figure 9). If the metric coefficients S and R have been specified, these integrals can be calculated and give us the light cone (see Figure 12 for an example). Having parametrized the rays with ${\hat g}$-arclength (= travel time), we immediately get the intersections of the light cone with hypersurfaces t = constant (“instantaneous wave fronts”); see Figures 13, 18, and 19.

Figure 6

Illustration of the exact lens map in spherically symmetric static spacetimes. The picture shows a spatial plane. The observation event (dot) is at r = r_O, static light sources are distributed at r = r_S. Θ is the colatitude coordinate on the observer’s sky. It takes values between 0 and π. Φ(Θ) is the angle swept out by the ray with initial direction Θ on its way from r_O to r_S. It takes values between 0 and ∞. In general, neither existence nor uniqueness of Φ(Θ) is guaranteed for given Θ. A similar picture is in [271]

4.3.4 Exact lens map

Recall from Section 2.1 that the exact lens map [123] refers to a chosen observation event p_O and a chosen “source surface” ${\mathcal T}$. In general, for ${\mathcal T}$ we may choose any 3-dimensional submanifold that is ruled by timelike curves. The latter are to be interpreted as wordlines of light sources. In a spherically symmetric and static spacetime, we may take advantage of the symmetry by choosing for ${\mathcal T}$ a sphere r = r_S with its ruling by the t-lines. This restricts the consideration to lensing for static light sources. Note that all static light sources at radius r_S undergo the same redshift, log(1 + z) = f (r_S) − f (r_O). Without loss of generality, we place the observation event p_O on the 3-axis at radius r_O. This gives us the past light cone in the representation (81). To each ray from the observer, with initial direction characterized by Θ, we can assign the total angle Φ(Θ) the ray sweeps out on its way from r_O to r_S (see Figure 6). Φ(Θ) is given by Equation (86),

$$\Phi (\Theta) = R({r_{\rm{O}}})\sin \Theta \int\nolimits_{{r_{\rm{O}}} \ldots}^{\ldots {{\rm{r}}_{\rm{S}}}} {{{S(r)dr} \over {R(r)\sqrt {R{{(r)}^2} - R{{({r_{\rm{O}}})}^2}{{\sin}^2}\Theta}}}},$$

(87)

where the same short-hand notation is used as in Equation (86). Φ(Θ) is not necessarily defined for all Θ because not all light rays that start at r_O may reach r_S. Also, Φ(Θ) may be multi-valued because a light ray may intersect the sphere r = r_S several times. Equation (81) gives us the (possibly multi-valued) lens map

$$(\Psi, \Theta) \mapsto \left({\begin{array}{*{20}c}{{{\rm{r}}_{\rm{S}}}{\rm{sin}}\Phi (\Theta){\rm{cos}}\Psi} \\ {{{\rm{r}}_{\rm{S}}}{\rm{sin}}\Phi (\Theta){\rm{sin}}\Psi} \\ {{{\rm{r}}_{\rm{S}}}{\rm{cos}}\Phi (\Theta)} \\ \end{array}} \right).$$

(88)

It assigns to each point on the observer’s sky the position of the light source which is seen at that point. Φ(Θ) may take all values between 0 and infinity. For each image we can define the order

$$i(\Theta) = \min \{m \in \mathbb{N}\vert \Phi (\Theta) < m\pi \},$$

(89)

which counts how often the ray has met the axis. The standard example where images of arbitrarily high order occur is the Schwarzschild spacetime (see Section 5.1). For many, though not all, applications one may restrict to the case that the spacetime is asymptotically flat and that r_O and r_S are so large that the spacetime is almost flat at these radius values. For a light ray with turning point at r_m(Θ), Equation (87) can then be approximated by

$$\Phi (\Theta) = 2\int\nolimits_{{r_m}(\Theta)}^\infty {{{S(r)dr} \over {R(r)\sqrt {R{{(r)}^2} - R{{({r_{\rm{O}}})}^2}{{\sin}^2}\Theta}}}}.$$

(90)

If the entire ray remains in the region where the spacetime is almost flat, Equation (90) gives the usual weak-field approximation of light bending with Φ(Θ) close to π. However, Equation (90) does not require that the ray stays in the region that is almost flat. The integral in Equation (90) becomes arbitrarily large if r_m(Θ) comes close to an unstable light sphere, R′(r_p) = 0 and R″(r_p) > 0. This situation is well known to occur in the Schwarzschild spacetime with r_p = 3m (see Section 5.1, in particular Figures 9, 14, and 15). The divergence of Φ(Θ) is always logarithmic [37]. Virbhadra and Ellis [337] (cf. [339] for an earlier version) approximately evaluate Equation (90) for the case that source and observer are almost aligned, i.e., that Φ(Θ) is close to an odd multiple of π. This corresponds to replacing the sphere at r_S with its tangent plane. The resulting “almost exact lens map” takes an intermediary position between the exact treatment and the quasi-Newtonian approximation. It was originally introduced for the Schwarzschild metric [337] where it approximates the exact treatment remarkably well within a wide range of validity [119]. On the other hand, neither analytical nor numerical evaluation of the “almost exact lens map” is significantly easier than that of the exact lens map. For situations where the assumption of almost perfect alignment cannot be maintained the Virbhadra-Ellis lens equation must be modified (see [70]; related material can also be found in [38]).

4.3.4.1 Distance measures, image distortion and brightness of images

For calculating image distortion (see Section 2.5) and the brightness of images (see Section 2.6) we have to consider infinitesimally thin bundles with vertex at the observer. In a spherically symmetric and static spacetime, we can apply the orthonormal derivative operators ∂_Θ and sin Θ∂_Ψ to the representation (81) of the past light cone. Along each ray, this gives us two Jacobi fields Y₁ and Y₂ which span an infinitesimally thin bundle with vertex at the observer. Y₁ points in the radial direction and Y₂ points in the tangential direction (see Figure 7). The radial and the tangential direction are orthogonal to each other and, by symmetry, parallel-transported along each ray. Thus, in contrast to the general situation of Figure 3, Y₁ and Y₂ are related to a Sachs basis (E₁, E₂) simply by Y₁ = and D₊ = D₋E₂. The coefficients D₊ and D₋ are the extremal angular diameter distances of Section 2.4 with respect to a static observer (because the (Ψ, Θ)-grid refers to a static observer). In the case at hand, they are called the radial and tangential angular diameter distances. They can be calculated by normalizing Y₁ and Y₂,

$$\begin{array}{*{20}c}{{D_ +}(\ell, \Theta) = {e^{f({\rm{r}}(\ell, \Theta))}}R({r_{\rm{O}}})\cos \Theta \sqrt {R{{({\rm{r(}}\ell, \Theta))}^2} - R(r_{\rm{O}}^2){{\sin}^2}\Theta}} \\{\times \int\nolimits_{{{\rm{r}}_{{\rm{O}} \ldots}}}^{\ldots {\rm{r(}}\Theta, \ell)} {{{S(r)R(r)dr} \over {{{\sqrt {R{{(r)}^2} - R{{({r_{\rm{O}}})}^2}{{\sin}^2}\Theta}}^3}}},}} \\ \end{array}$$

(91)

$${D_ -}(\ell, \Theta) = {e^{f({\rm{r}}(\ell, \Theta))}}R({\rm{r}}(\ell, \Theta)){{\sin \phi (\ell, \Theta)} \over {\sin \Theta}}.$$

(92)

These formulas have been derived first for the special case of the Schwarzschild metric by Dwivedi and Kantowski [84] and then for arbitrary spherically symmetric static spacetimes by Dyer [85]. (In [85], Equation (92) is erroneously given only for the case that, in our notation, e^f(r)R(r) = r.) From these formulas we immediately get the area distance ${D_{{\rm{area}}}} = \sqrt {\left\vert {{D_ +}{D_ -}} \right\vert}$ for a static observer and, with the help of the redshift z, the luminosity distance D_lum = (1 + z)²D_area (recall Section 2.4). In this way, Equation (91) and Equation (92) allow to calculate the brightness of images according to the formulas of Section 2.6. Similarly, Equation (91) and Equation (92) allow to calculate image distortion in terms of the ellipticity ε (recall Section 2.5). In general, ε is a complex quantity, defined by Equation (49). In the case at hand, it reduces to the real quantity ε = D₋/D₊ − D₊/D₋. The expansion θ and the shear a of the bundles under consideration can be calculated from Kantowski’s formula [173, 84],

$${\dot D_ \pm} = (\theta \pm \sigma){D_ \pm},$$

(93)

to which Equation (27) reduces in the case at hand. The dot (= derivative with respect to the affine parameter s) is related to the derivative with respect to ℓ by Equation (83). Evaluating Equations (91, 92) in connection with the exact lens map leads to quite convenient formulas, for static light sources at r = r_S. Setting r(ℓ, Θ) = r_S and φ(ℓ, Θ) = Φ(Θ) and comparing with Equation (87) yields (cf. [271])

$${D_ +}(\Theta) = {e^{f({r_{\rm{S}}})}}\sqrt {R{{({r_{\rm{S}}})}^2} - R{{({r_{\rm{O}}})}^2}{{\sin}^2}\Theta} \Phi{\prime}(\Theta),$$

(94)

$${D_ -}(\Theta) = {e^{f({r_{\rm{S}}})}}R({r_{\rm{S}}})\sin \Phi (\Theta).$$

(95)

These formulas immediately give image distortion and the brightness of images if the map Θ ↦ Φ(Θ) is known.

Figure 7

Thin bundle around a ray in a spherically symmetric static spacetime. The picture is purely spatial, i.e., the time coordinate t is not shown. The ray is contained in a plane, so there are two distinguished spatial directions orthogonal to the ray: the “radial” direction (in the plane) and the “tangential” direction (orthogonal to the plane). For a bundle with vertex at the observer, the radial diameter of the cross-section gives the radial angular diameter distance D₊, and the tangential diameter of the cross-section gives the tangential angular diameter distance D₋. In contrast to the general situation of Figure 3, here the angle χ is zero (if the Sachs basis (E₁, E₂) is chosen appropriately). Recall that D₊ and D₋ are positive up to the first caustic point.

4.3.5 Caustics of light cones

Quite generally, the past light cone has a caustic point exactly where at least one of the extremal angular diameter distances D₊, D₋ vanishes (see Sections 2.2, 2.3, and 2.4). In the case at hand, zeros of D₊ are called radial caustic points and zeros of D₋ are called tangential caustic points (see Figure 8). By Equation (92), tangential caustic points occur if φ(ℓ, Θ) is a multiple of n, i.e., whenever a light ray crosses the axis of symmetry through the observer (see Figure 8). Symmetry implies that a point source is seen as a ring (“Einstein ring”) if its worldline crosses a tangential caustic point. By contrast, a point source whose wordline crosses a radial caustic point is seen infinitesimally extended in the radial direction. The set of all tangential caustic points of the past light cone is called the tangential caustic for short. In general, it has several connected components (“first, second, etc. tangential caustic”). Each connected component is a spacelike curve in spacetime which projects to (part of) the axis of symmetry through the observer. The radial caustic is a lightlike surface in spacetime unless at points where it meets the axis; its projection to space is rotationally symmetric around the axis. The best known example for a tangential caustic, with infinitely many connected components, occurs in the Schwarzschild spacetime (see Figure 12). It is also instructive to visualize radial and tangential caustics in terms of instantaneous wave fronts, i.e., intersections of the light cone with hypersurfaces t = constant. Examples are shown in Figures 13, 18, and 19. By symmetry, a tangential caustic point of an instantaneous wave front can be neither a cusp nor a swallow-tail. Hence, the general result of Section 2.2 implies that the tangential caustic is always unstable. The radial caustic in Figure 19 consists of cusps and is, thus, stable.

Figure 8

Tangential and radial caustic points. Tangential caustic points, D₋ = 0, occur on the axis of symmetry through the observer. A (point) source at a tangential caustic point is seen as a (1-dimensional) Einstein ring on the observer’s sky. A point source at a radial caustic point, D₊ = 0, appears “infinitesimally extended” in the radial direction.

4.4 Lensing in axisymmetric stationary spacetimes

Axisymmetric stationary spacetimes are of interest in view of lensing as general-relativistic models for rotating deflectors. The best known and most important example is the Kerr metric which describes a rotating black hole (see Section 5.8). For non-collapsed rotating objects, exact solutions of Einstein’s field equation are known only for the idealized cases of infinitely long cylinders (including string models; see Section 5.10) and disks (see Section 5.9). Here we collect, as a preparation for these examples, some formulas for an unspecified axisymmetric stationary metric. The latter can be written in coordinates (y¹, y², ϕ, t), with capital indices A, B, … taking the values 1 and 2, as

$$g = g\_\{tt\} (y)d{t^2} + 2g{t_\varphi}(y)dt{d_\varphi} + {g_{\varphi \phi}}(y)d{\varphi ^2} + {g_{AB}}(y)d{y^A}d{y^B},$$

(96)

where all metric coefficients depend on y = (y¹, y²) only. We assume that the integral curves of ∂_ϕ are closed, with the usual (2_π)-periodicity, and that the 2-dimensional orbits spanned by ∂_ϕ and ∂_t are timelike. Then the Lorentzian signature of g implies that g_AB (y) is positive definite. In general, the vector field ∂_t need not be timelike and the hypersurfaces t = constant need not be spacelike. Our assumptions allow for transformations (ϕ, t) ↦ Ωt, t) with a constant Ω. If, by such a transformation, we can achieve that g_tt < 0 everywhere, we can use the purely spatial formalism for light rays in terms of the Fermat geometry (recall Section 4.2). Comparison of Equation (96) with Equation (61) shows that the redshift potential f, the Fermat metric ${\hat g}$, and the Fermat one-form ${\hat \phi}$ are

$${e^{2f}} = - {g_{tt}},$$

(97)

$$\hat g = - {{{g_{AB}}} \over {{g_{tt}}}}d{x^A}d{x^B} + {{g_{t\varphi}^2 - {g_{tt}}{g_{\varphi \varphi}}} \over {g_{tt}^2}}d{\varphi ^2},$$

(98)

$$\hat \phi = - {{{g_{t\varphi}}} \over {{g_{tt}}}}d\varphi,$$

(99)

respectively. If it is not possible to make g_tt negative on the entire spacetime domain under consideration, the Fermat geometry is defined only locally and, therefore, of limited usefulness. This is the case, e.g., for the Kerr metric where, in Boyer-Lindquist coordinates, g_tt is positive in the ergosphere (see Section 5.8).

Variational techniques related to Fermat’s principal in stationary spacetimes are detailed in a book by Masiello [218]. Note that, in contrast to standard terminology, Masiello’s definition of stationarity includes the assumption that the surfaces t = constant are spacelike.

For a rotating body with an equatorial plane (i.e., with reflectional symmetry), the Fermat metric of the equatorial plane can be represented by an embedding diagram, in analogy to the spherically symmetric static case (recall Figure 11). However, one should keep in mind that in the non-static case the lightlike geodesics do not correspond to the geodesics of ${\hat g}$ but are affected, in addition, by a sort of Coriolis force produced by ${\hat \phi}$. For a review on embedding diagrams, including several examples (see [160]).

5 Examples

5.1 Schwarzschild spacetime

The (exterior) Schwarzschild metric

$$g = - \left({1 - {{2m} \over r}} \right)d{t^2} + {\left({1 - {{2m} \over r}} \right)^{- 1}}d{r^2} + {r^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\varphi ^2})$$

(100)

has the form (69) with

$${e^{2f(r)}} = S{(r)^{- 1}} = 1 - {{2m} \over r},\quad R(r) = {r \over {\sqrt {1 - {{2m} \over r}}}}.$$

(101)

It is the unique spherically symmetric vacuum solution of Einstein’s field equation. At the same time, it is the most important and best understood spacetime in which lensing can be explicitly studied without approximations. Schwarzschild lensing beyond the weak-field approximation has astrophysical relevance in view of black holes and neutron stars. The increasing evidence that there is a supermassive black hole at the center of our Galaxy (see [107] for background material) is a major motivation for a detailed study of Schwarzschild lensing (and of Kerr lensing; see Section 5.8). In the following we consider the Schwarzschild metric with a constant m > 0 and we ignore the region r < 0 for which the singularity at r = 0 is naked. The Schwarzschild metric is static on the region 2m < r < ∞. (The region r < 0 for m > 0 is equivalent to the region r > 0 for m < 0. It is usually considered as unphysical but has found some recent interest in connection with lensing by wormholes; see Section 5.4.)

5.1.1 Historical notes

Shortly after the discovery of the Schwarzschild metric by Schwarzschild [302] and independently by Droste [80], basic features of its lightlike geodesics were found by Flamm [114], Hilbert [158], and Weyl [347]. Detailed studies of its timelike and lightlike geodesics were made by Hagihara [146] and Darwin [72, 73]. For a fairly complete list of the pre-1979 literature on Schwarzschild geodesics see Sharp [306]. All modern text-books on general relativity include a section on Schwarzschild geodesics, but not all of them go beyond the weak-field approximation. For a particularly detailed exposition see Chandrasekhar [54].

5.1.2 Redshift and Fermat geometry

The redshift potential f for the Schwarzschild metric is given in Equation (101). With the help of f we can directly calculate the redshift via Equation (68) if observer and light source are static (i.e., t-lines). If the light source or the observer does not follow a t-line, a Doppler factor has to be added. Independent of the velocity of observer and light source, the redshift becomes arbitrarily large if the light source is sufficiently close to the horizon. For light source and observer freely falling, the redshift formula was discussed by Bazanski and Jaranowski [24]. If projected to 3-space, the light rays in the Schwarzschild spacetime are the geodesics of the Fermat metric which can be read from Equation (70) (cf. Frankel [116]),

$$\hat g = {{d{r^2}} \over {{{\left({1 - {{2m} \over r}} \right)}^2}}} + {{{r^2}(d{\vartheta ^2}) + \sin \vartheta d{\varphi ^2}} \over {1 - {{2m} \over r}}}.$$

(102)

The metric coefficient R(r), as given by Equation (101), has a strict minimum at r = 3m and no other extrema (see Figure 9). Hence, there is an unstable light sphere at this radius (recall Equation (71)). The existence of circular light rays at r = 3m was noted already by Hilbert [158]. The relevance of these circular light rays in view of lensing was clearly seen by Darwin [72, 73] and Atkinson [13]. They realized, in particular, that a Schwarzschild black hole produces infinitely many images of each light source, corresponding to an infinite sequence of light rays that asymptotically spiral towards a circular light ray. The circular light rays at r = 3m are also associated with other physical effects such as centrifugal force reversal and “locking” of gyroscopes. These effects have been discussed with the help of the Fermat geometry (= optical reference geometry) in various articles by Abramowicz and collaborators (see, e.g., [5, 4, 6, 2]).

Figure 9

The function R(r) for the Schwarzschild metric. Light rays that start at r_O with initial direction Θ are confined to the region where R(r) ≥ R(r_O) sin Θ. The equation R(3m) = R(r_O) sin δ defines for each r_O a critical value δ. A light ray from r_O with Θ = δ asymptotically approaches r = 3m.

5.1.3 Index of refraction and embedding diagrams

We know from Section 4.3 that light rays in any spherically symmetric and static spacetime can be characterized by an index of refraction. This requires introducing an isotropic radius coordinate ${\tilde r}$ via Equation (72). In the Schwarzschild case, ${\tilde r}$ is related to the Schwarzschild radius coordinate r by

$$\tilde r = {1 \over 2}\left({\sqrt {{r^2} - 2mr} + r - m} \right),\quad r = {{{{(2\tilde r + m)}^2}} \over {4\tilde r}}.$$

(103)

${\tilde r}$ ranges from m/2 to infinity if r ranges from 2m to infinity. In terms of the isotropic coordinate, the Fermat metric (102) takes the form

$$\hat g = n{(\tilde r)^2}(d{\tilde r^2} + {\tilde r^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\varphi ^2}))$$

(104)

with

$$n(\tilde r) = {\left({1 + {m \over {2\tilde r}}} \right)^3}{\left({1 - {m \over {2\tilde r}}} \right)^{- 1}}.$$

(105)

Hence, light propagation in the Schwarzschild metric can be mimicked by the index of refraction (105); see Figure 10. The index of refraction (105) is known since Weyl [349]. It was employed for calculating lightlike Schwarzschild geodesics, exactly or approximately, e.g., in [13, 231, 106, 204]. This index of refraction can be modeled by a fluid flow [288]. The embeddability condition (75) is satisfied for r > 2.25m (which coincides with the so-called Buchdahl limit). On this domain the Fermat geometry, if restricted to the equatorial plane ϑ = π/2, can be represented as a surface of revolution in Euclidean 3-space (see Figure 11). The entire region r > 2m can be embedded into a space of constant negative curvature [3].

Figure 10

Index of refraction $n(\tilde r)$, given by Equation (105) , for the Schwarzschild metric as a function of the isotropic coordinate ${\tilde r}$.

Figure 11

Fermat geometry of the equatorial plane of the Schwarzschild spacetime, embedded as a surface of revolution into Euclidean 3-space. The neck is at r = 3m (i.e., $\tilde r \approx 1.87m$), the boundary of the embeddable part at r = 2.25m (i.e., $\tilde r = m$). The geodesics of this surface of revolution give the light rays in the Schwarzschild spacetime. A similar figure can be found in [4] (also cf. [160]).

5.1.4 Lensing by a Schwarzschild black hole

To get a Schwarzschild black hole, one joins at r = 2m the static Schwarzschild region 2m < r < ∞ to the non-static Schwarzschild region 0 < r < 2m in such a way that ingoing light rays can cross this surface but outgoing cannot. If the observation event p_O is at r_O > 2m, only the region r > 2m is of relevance for lensing, because the past light cone of such an event does not intersect the black-hole horizon at r = 2m. (For a Schwarzschild white hole see below.) Such a light cone is depicted in Figure 12 (cf. [183]). The picture was produced with the help of the representation (81) which requires integrating Equation (85) and Equation (86). For the Schwarzschild case, these are elliptical integrals. Their numerical evaluation is an exercise for students (see [45] for a MATHEMATICA program). Note that the evaluation of Equation (85) and Equation (86) requires knowledge of the turning points. In the Schwarzschild case, there is at most one turning point r_m(Θ) along each ray (see Figure 9), and it is given by the cubic equation

$${r_m}{(\Theta)^3}({r_{\rm{O}}} - 2m) - {r_m}(\Theta)r_{\rm{O}}^3{\sin ^2}\Theta + 2mr_{\rm{O}}^3{\sin ^2}\Theta = 0.$$

(106)

The representation (81) in terms of Fermat arclength ℓ (= travel time) gives us the intersections of the light cone with hypersurfaces t = constant. These “instantaneous wave fronts” are depicted in Figure 13 (cf. [147]). With the light cone explicitly known, one can analytically verify that every inextendible timelike curve in the region r > 2m intersects the light cone infinitely many times, provided it is bounded away from the horizon and from (past lightlike) infinity. This shows that the observer sees infinitely many images of a light source with this worldline. The same result can be proven with the help of Morse theory (see Section 3.3), where one has to exclude the case that the worldline meets the caustic of the light cone. In the latter case the light source is seen as an Einstein ring. For static light sources (i.e., t-lines), either all images are Einstein rings or none. For such light sources we can study lensing in the exact-lens-map formulation of Section 4.3 (see in particular Figure 6). Also, Section 4.3 provides us with formulas for distance measures, brightness, and image distortion which we just have to specialize to the Schwarzschild case. For another treatment of Schwarzschild lensing with the help of the exact lens map, see [119]. We place our static light sources at radius r_S. If r_O < r_S and 3m < r_S, only light rays with Θ < δ,

$$\sin \delta: = {{R(3m)} \over {R({r_{\rm{O}}})}} = \sqrt {{{27{m^2}({r_{\rm{O}}} - 2m)} \over {r_{\rm{O}}^3}}},$$

(107)

can reach the radius value r_S (see Figure 9). Rays with Θ = δ asymptotically spiral towards the light sphere at r = 3m. δ lies between 0 and π/2 for r_O < 3m and between π/2 and π for r_O > 3m. The escape cone defined by Equation (107) is depicted, for different values of r_O, in Figure 14. It gives the domain of definition for the lens map. The lens map is graphically discussed in Figure 15. The pictures are valid for r_O = 5m and r_S = 10m. Qualitatively, however, they look the same for all cases with r_S > r_O and r_S > 3m. From the diagram one can read the position of the infinitely many images for each light source which, for the two light sources on the axis, degenerate into infinitely many Einstein rings. For each fixed source, the images are ordered by the number i (= 1, 2, 3, …) which counts how often the ray has met the axis. This coincides with ordering according to travel time. With increasing order i, the images come closer and closer to the rim at Θ = δ (see Figure 15). They are alternately upright and side-inverted (see Figure 16), and their brightness rapidly decreases (see Figure 17). These basic features of Schwarzschild lensing are known since pioneering papers by Darwin [72] and Atkinson [13] (cf. [211, 246, 201]). A detailed study of Schwarzschild lensing was carried through by Virbhadra and Ellis [337] with the help of an “almost exact lens map” (see Section 4.3). The latter assumes that observer and light source are in the asymptotic region and almost aligned, but the light rays are allowed to make arbitrarily many turns around the black hole. Various methods of how multiple imaging by a black hole could be discovered, directly or indirectly, have been discussed [211, 201, 15, 14, 274, 76]. Related work has also been done for Kerr black holes (see Section 5.8). An interesting suggestion was made in [162]. A Schwarzschild black hole, somewhere in the universe, would send photons originating from our Sun back to the vicinity of our Sun (“boomerang photons” [316]). If the black hole is sufficiently close to our Solar system, this would produce images of our own Sun on the sky that could be detectable. The lensing effect of a Schwarzschild black hole has been visualized in two ways:

• 1. by showing the visual appearance of some background pattern as distorted by the black hole [66, 296, 233] (only primary images, i = 1, are considered), and

• 2. by showing the visual appearence of an accretion disk around the black hole [211, 130, 15, 14] (higher-order images are taken into account).

Numerous ray tracing programs have been developed for the Schwarzschild metric and, more generally, for the Kerr metric (see Section 5.8).

Figure 12

Past light cone in the Schwarzschild spacetime. One sees that the light cone wraps around the horizon, then forms a tangential caustic. In the picture the caustic looks like a transverse self-intersection because one spatial dimension is suppressed. (Only the hyperplane ϑ = π/2 is shown.) There is no radial caustic. If one follows the light rays further back in time, the light cone wraps around the horizon again and again, thereby forming infinitely many tangential caustics which alternately cover the radius line through the observer and the radius line opposite to the observer. In spacetime, each caustic is a spacelike curve along which r ranges from 2m to ∞, whereas t ranges from −∞ to some maximal value and then back to −∞. Equal-time sections of this light cone are shown in Figure 13 .

Figure 13

Instantaneous wave fronts of the light cone in the Schwarzschild spacetime. This picture shows intersections of the light cone in Figure 12 with hypersurfaces t = constant for four t-values, with t₁ > t₂ > t₃ > t₄. The instantaneous wave fronts wrap around the horizon and, after reaching the first caustic, have two caustic points each. If one goes further back in time than shown in the picture, the wave fronts another time wrap around the horizon, reach the second caustic, and now have four caustic points each, and so on. In comparison to Figure 12 , the representation in terms of instantaneous wave fronts has the advantage that all three spatial dimensions are shown.

Figure 14

Escape cones in the Schwarzschild metric, for five values of r_O. For an observer at radius r_O, light sources distributed at a radius r_S with r_S > ro and r_S > 3m illuminate a disk whose angular radius δ is given by Equation (107 ). The boundary of this disk corresponds to light rays that spiral towards the light sphere at r = 3m. The disk becomes smaller and smaller for r_O → 2m. Figure 9 illustrates that the notion of escape cones is meaningful for any spherically symmetric and static spacetime where R has one minimum and no other extrema [253]. For the Schwarzschild spacetime, the escape cones were first mentioned in [249, 223], and explicitly calculated in [320]. A picture similar to this one can be found, e.g., in [54].

Figure 15

Lens map for the Schwarzschild metric. The observer is at r_O = 5m, the light sources are at r_S = 10m. Θ is the colatitude on the observer’s sky and Φ(Θ) is the angle swept out by the ray (see Figure 6 ). Φ(Θ) was calculated with the help of Equation (87) . Θ is restricted by the opening angle δ of the observer’s escape cone (see Figure 14 ). Rays with Θ = δ asymptotically spiral towards the light sphere at r = 3m. The first diagram (cf. [119], Figure 5 ) shows that Φ(Θ) ranges from 0 to ∞ if Θ ranges from 0 to δ. So there are infinitely many Einstein rings (dashed lines) whose angular radius approaches δ. One can analytically prove [211, 246, 39] that the divergence of Φ(Θ) for Θ → δ is logarithmic. This is true whenever light rays approach an unstable light sphere [37]. The second diagram shows Φ(Θ) over a logarithmic Θ-axis. The graph of Φ approaches a straight line which was called the “strong-field limit” by Bozza et al. [39, 37]. The picture illustrates that it is a good approximation for all light rays that make at least one full turn. The third diagram shows cosΦ(Θ) over a logarithmic Θ-axis. For every source position 0 < ϑ < π one can read the position of the images (dotted line). There are infinitely many, numbered by their order (89) that counts how often the light ray has crossed the axis. Images of odd order are on one side of the black hole, images of even order on the other. For the sources at ϑ = π and ϑ = 0 one can read the positions of the Einstein rings.

Figure 16

Radial angular diameter distance D₊(O), tangential angular diameter distance D₋(Θ) and travel time T(Θ) in the Schwarschild spacetime. The data are the same as in Figure 15 . For the definition of D₊ and D₋ see Figure 7 . D_±(Θ) can be calculated from Φ(Θ) with the help of Equation (94) and Equation (95) . For the Schwarzschild case, the resulting formulas are due to [84] (cf. [85, 119]). Zeros of D₋ indicate Einstein rings. If D₊ and D₋ have different signs, the observer sees a side-inverted image. The travel time T(Θ) (= Fermat arclength) can be calculated from Equation (85) . One sees that, over the logarithmic Θ-axis used here, the graph of T approaches a straight line. This illustrates that T(Θ) diverges logarithmically if Θ approaches its limiting value δ. This can be verified analytically and is characteristic of all cases where light rays approach an unstable light sphere [40].

Figure 17

Luminosity distance D_lum(Θ) and ellipticity ε(Θ) (image distortion) in the Schwarzschild spacetime. The data are the same as in Figures 15 and 16 . If point sources off equal bolometric luminosity are distributed at r = r_S, the plotted function 2.5 log₁₀ (D_lum(Θ)²) gives their magnitude on the observer’s sky, modulo an additive constant m₀. For the calculation of D_lum one needs D₊ and D₋ (see Figure 16 ), and the general relations (41) and (48) . This procedure follows [84] (cf. [85, 119]). For source and observer at large radius, related calculations can also be found in [211, 246, 201, 337]. Einstein rings have magnitude −∞ in the ray-optical treatment. For a light source not on the axis, the image of order i + 2 is fainter than the image of order i by 2.5 log₁₀(e^2π) ≈ 6.8 magnitudes, see [211, 246]. (This is strictly true in the “strong-field limit”, or “strong-bending limit”, which is explained in the caption of Figure 15 .) The above picture is similar to Figure 6 in [246]. Note that it refers to point sources and not to a radiating spherical surface r = r_S of constant surface brightness; by Equation (54) , the latter would show a constant intensity. The lower part of the diagram illustrates image distortion in terms of $\varepsilon = {{{D_ -}} \over {{D_ +}}} - {{{D_ +}} \over {{D_ -}}}$. Clearly, |ε| is infinite at each Einstein ring. The double-logarithmic representation shows that beyond the second Einstein ring all images are extremely elongated in the tangential direction, |ε| > 100. Image distortion in the Schwarzschild spacetime is also treated in [85, 121, 120], an approximation formula is derived in [240].

5.1.5 Lensing by a non-transparent Schwarzschild star

To model a non-transparent star of radius r_* one has to restrict the exterior Schwarzschild metric to the region r > r_*. Lightlike geodesics terminate when they arrive at r = r_*. The star’s radius cannot be smaller than 2m unless it is allowed to be time-dependent. The qualitative features of lensing depend on whether r_* is bigger than 3m. Stars with 2m < r_* ≤ 3m are called ultracompact [166]. Their existence is speculative. The lensing properties of an ultracompact star are the same as that of a Schwarzschild black hole of the same mass, for observer and light source in the region r > r_*. In particular, the apparent angular radius δ on the observer’s sky of an ultracompact star is given by the escape cone of Figure 14. Also, an ultracompact star produces the same infinite sequence of images of each light source as a black hole. For r_* > 3m, only finitely many of the images survive because the other lightlike geodesics are blocked. A non-transparent star has a finite focal length r_f > 2m in the sense that parallel light from infinity is focused along a line that extends from radius value r_f to infinity. r_f depends on m and on r_*. For the values of our Sun one finds r_f = 550 au (1 au = 1 astronomical unit = average distance from the Earth to the Sun). An observer at r ≥ r_f can observe strong lensing effects of the Sun on distant light sources. The idea of sending a spacecraft to r ≥ r_f was occasionally discussed in the literature [103, 234, 326]. The lensing properties of a non-transparent Schwarzschild star have been illustrated by showing the appearance of the star’s surface to a distant observer. For r_* bigger than but of the same order of magnitude as 3m, this has relevance for neutron stars (see [352, 256, 129, 287, 221,]). r_* may be chosen time-dependent, e.g., to model a non-transparent collapsing star. A star starting with r_* > 2m cannot reach r = 2m in finite Schwarzschild coordinate time t (though in finite proper time of an observer at the star’s surface), i.e., for a collapsing star one has r_*(t) ↦ 2m for t → ∞. To a distant observer, the total luminosity of a freely (geodesically) collapsing star is attenuated exponentially, $L(t) \propto \exp (- t(3\sqrt 3 m) - 1)$. This formula was first derived by Podurets [279] with an incorrect factor 2 under the exponent and corrected by Ames and Thorne [8]. Both papers are based on kinetic photon theory (Liouville’s equation). An alternative derivation of the luminosity formula, based on the optical scalars, was given by Dwivedi and Kantowski [84]. Ames and Thorne also calculated the spectral distribution of the radiation as a function of time and position on the apparent disk of the star. All these analyses considered radiation emitted at an angle < π/2 against the normal of the star as measured by a static (Killing) observer. Actually, one has to refer not to a static observer but to an observer comoving with the star’s surface. This modification was worked out by Lake and Roeder [198].

5.1.6 Lensing by a transparent Schwarzschild star

To model a transparent star of radius r_* one has to join the exterior Schwarzschild metric at r = r_* to an interior (e.g., perfect fluid) metric. Lightlike geodesics of the exterior Schwarzschild metric are to be joined to lightlike geodesics of the interior metric when they arrive at r = r_*. The radius r_* of the star can be time-independent only if r_* > 2m. For 2m < r_* ≤ 3m (ultracompact star), the lensing properties for observer and light source in the region r > r_* differ from the black hole case only by the possible occurrence of additional images, corresponding to light rays that pass through the star. Inside such a transparent ultracompact star, there is at least one stable photon sphere, in addition to the unstable one at r = 3m outside the star (cf. [153]). In principle, there may be arbitrarily many photon spheres [177]. For r_* > 3m, the lensing properties depend on whether there are light rays trapped inside the star. For a perfect fluid with constant density, this is not the case; the resulting spacetime is then asymptotically simple, i.e., all inextendible light rays come from infinity and go to infinity. General results (see Section 3.4) imply that then the number of images must be finite and odd. The light cone in this exterior-plus-interior Schwarzschild spacetime is discussed in detail by Kling and Newman [183]. (In this paper the authors constantly refer to their interior metric as to a “dust” where obviously a perfect fluid with constant density is meant.) Effects on light rays issuing from the star’s interior have been discussed already earlier by Lawrence [203]. The “escape cones”, which are shown in Figure 14 for the exterior Schwarzschild metric have been calculated by Jaffe [167] for points inside the star. The focal length of a transparent star with constant density is smaller than that of a non-transparent star of the same mass and radius. For the mass and the radius of our Sun, one finds 30 au for the transparent case, in contrast to the above-mentioned 550 au for the non-transparent case [234]. Radiation from a spherically symmetric homogeneous dust star that collapses to a black hole is calculated in [305], using kinetic theory. An inhomogeneous spherically symmetric dust configuration may form a naked singularity. The redshift of light rays that travel from such a naked singularity to a distant observer is discussed in [83].

5.1.7 Lensing by a Schwarzschild white hole

To get a Schwarzschild white hole one joins at r = 2m the static Schwarzschild region 2m < r < ∞ to the non-static Schwarzschild region 0 < r < 2m at r = 2m in such a way that outgoing light rays can cross this surface but ingoing cannot. The appearance of light sources in the region r < 2m to an observer in the region r > 2m is discussed in [112, 232, 81, 196, 197].

5.2 Kottler spacetime

The Kottler metric

$$g = - \left({1 - {{2m} \over r} - {{\Lambda {r^2}} \over 3}} \right)d{t^2} + {{d{r^2}} \over {1 - {{2m} \over r} - {{\Lambda {r^2}} \over 3}}} + {r^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\vartheta ^2})$$

(108)

is the unique spherically symmetric solution of Einstein’s vacuum field equation with a cosmological constant A. It has the form (69) with

$${e^{2f(r)}} = S{(r)^{- 1}} = 1 - {{2m} \over r} - {{\Lambda {r^2}} \over 3},\quad \,R(r) = {r \over {1 - {{2m} \over r} - {{\Lambda {r^2}} \over 3}}}.$$

(109)

It is also known as the Schwarzschild-deSitter metric for Λ > 0 and as the Schwarzschild-antideSitter metric for Λ < 0. The Kottler metric was found independently by Kottler [186] and by Weyl [348].

In the following we consider the Kottler metric with a constant m > 0 and we ignore the region r < 0 for which the singularity at r = 0 is naked, for any value of Λ. For Λ < 0, there is one horizon at a radius r_H with 0 < r_H < 2m; the staticity condition e^f(r) > 0 is satisfied on the region r_H < r < ∞. For 0 < Λ < (3m)⁻², there are two horizons at radii r_H1 and r_H2 with 2m < r_H1 < 3m < r_H2; the staticity condition e^f(r) > 0 is satisfied on the region r_H1 < r < r_H2. For Λ > (3m)⁻² there is no horizon and no static region. At the horizon(s), the Kottler metric can be analytically extended into non-static regions. For Λ < 0, the resulting global structure is similar to the Schwarzschild case. For 0 < Λ < (3m)⁻², the resulting global structure is more complex (see [195]). The extreme case Λ = (3m)⁻² is discussed in [278].

For any value of Λ, the Kottler metric has a light sphere at r = 3m. Escape cones and embedding diagrams for the Fermat geometry (optical geometry) can be found in [314, 160] (cf. Figures 14 and 11 for the Schwarzschild case). Similarly to the Schwarzschild spacetime, the Kottler spacetime can be joined to an interior perfect-fluid metric with constant density. Embedding diagrams for the Fermat geometry (optical geometry) of the exterior-plus-interior spacetime can be found in [315]. The dependence on Λ of the light bending is discussed in [194]. For the optical appearance of a Kottler white hole see [196]. The shape of infinitesimally thin light bundles in the Kottler spacetime is determined in [85].

5.3 Reissner-Nordström spacetime

The Reissner-Nordström metric

$$g = - \left({1 - {{2m} \over r} + {{{e^2}} \over {{r^2}}}} \right)d{t^2} + {{d{r^2}} \over {1 - {{2m} \over r} + {{{e^2}} \over {{r^2}}}}} + {r^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\varphi ^2})$$

(110)

is the unique spherically symmetric and asymptotically flat solution of the Einstein-Maxwell equations. It has the form (69) with

$${e^{2f(r)}} = S{(r)^{- 1}} = 1 - {{2m} \over r} + {{{e^2}} \over {{r^2}}},\quad R(r) = {r \over {1 - {{2m} \over r} + {{{e^2}} \over {{r^2}}}}}.$$

(111)

It describes the field around an isolated spherical object with mass m and charge e. The Reissner-Nordström metric was found independently by Reissner [286], Weyl [347], and Nordström [241]. A fairly complete list of the pre-1979 literature on Reissner-Nordström geodesics can be found in [306]. A detailed account of Reissner-Nordström geodesics is given in [54]. (The Reissner-Nordström spacetime can be modified by introducing a cosmological constant. This generalized Reissner-Nordström spacetime, whose global structure is investigated in [202], will not be considered here.)

We assume m > 0 and ignore the region r < 0 for which the singularity at r = 0 is naked, for any value of e. Two cases are to be distinguished:

• 1. 0 ≤ e² ≤ m²; in this case the staticity condition e^f(r) > 0 is satisfied on the regions $0 < r < m - \sqrt {{m^2} - {e^2}}$ and $m + \sqrt {{m^2} - {e^2}} < r < \infty$, i.e., there are two horizons.

• 2. m² < e²; then the staticity condition e^f(r) > 0 is satisfied on the entire region 0 < r < ∞, i.e., there is no horizon and the singularity at r = 0 is naked.

As the net charge of all known celestial bodies is close to zero, the naked-singularity case 2 is usually thought to be of little astrophysical relevance.

By switching to isotropic coordinates, one can describe light propagation in the Reissner-Nordström metric by an index of refraction (see, e.g., [105]). The resulting Fermat geometry (optical geometry) is discussed, in terms of embedding diagrams for the black-hole case and for the naked-singularity case, in [191, 3] (cf. [160]). The visual appearance of a background, as distorted by a Reissner-Nordström black hole, is calculated in [222]. Lensing by a charged neutron star, whose exterior is modeled by the Reissner-Nordström metric, is the subject of [68, 69]. The lensing properties of a Reissner-Nordström black hole are qualitatively (though not quantitatively) the same as that of a Schwarzschild black hole. The reason is the following. For a Reissner-Nordström black hole, the metric coefficient R(r) has one local minimum and no other extremum between horizon and infinity, just as in the Schwarzschild case (recall Figure 9). The minimum of R(r) indicates an unstable light sphere towards which light rays can spiral asymptotically. The existence of this minimum, and of no other extremum, was responsible for all qualitative features of Schwarzschild lensing. Correspondingly, Figures 15, 16, and 17 also qualitatively illustrate lensing by a Reissner-Nordström black hole. In particular, there is an infinite sequence of images for each light source, corresponding to an infinite sequence of light rays whose limit curve asymptotically spirals towards the light sphere. One can consider the “strong-field limit” [39, 37] of lensing for a Reissner-Nordström black hole, in analogy to the Schwarzschild case which is indicated by the asymptotic straight line in the middle graph of Figure 15. Bozza [37] investigates whether quantitative features of the “strong-field limit”, e.g., the slope of the asymptotic straight line, can be used to distinguish between different black holes. For the Reissner-Nordström black hole, image positions and magnifications have been calculated in [96], and travel times have been calculated in [290]. In both cases, the authors use the “almost exact lens map” of Virbhadra and Ellis [337] (recall Section 4.3) and analytical methods of Bozza et al. [39, 37, 40].

5.4 Morris-Thorne wormholes

We consider a spacetime whose metric is of the form (69) with e^f(r)S(r) = 1, i.e.,

$$g = - {e^{2f(r)}}d{t^2} + d{r^2} + {e^{2f(r)}}R{(r)^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\varphi ^2}),$$

(112)

where r ranges from −∞ to ∞. We call such a spacetime a Morris-Thorne wormhole (see [227]) if

$$f(r)\underset {r \rightarrow \pm \infty} \rightarrow 0,\quad {r^{- 2}}R{(r)^2}\underset {r \rightarrow \pm \infty} \rightarrow 1,$$

(113)

such that the metric (112) is asymptotically flat for r → −∞ and for r → ∞.

A particular example of a Morris-Thorne wormhole is the Ellis wormhole [102] where

$$f(r) = 0,\quad R(r) = \sqrt {{r^2} + {a^2}}$$

(114)

with a constant a. The Ellis wormhole has an unstable light sphere at r = 0, i.e., at the “neck” of the wormhole. It is easy to see that every Morris-Thorne wormhole must have an unstable light sphere at some radius between r = −∞ and r = ∞. This has the consequence [153] that every Morris-Thorne wormhole produces an infinite sequence of images of an appropriately placed light source. This infinite sequence corresponds to infinitely many light rays whose limit curve asymptotically spirals towards the unstable light sphere.

Lensing by the Ellis wormhole was discussed in [55]; in this paper the authors identified the region r > 0 with the region r < 0 and they developed a scattering formalism, assuming that observer and light source are in the asymptotic region. Lensing by the Ellis wormhole was also discussed in [271] in terms of the exact lens map. The resulting features are qualitatively very similar to the Schwarzschild case, with the radius values r = −∞, r = 0, r = ∞ in the wormhole case corresponding to the radius values r = 2m, r = 3m, r = ∞ in the Schwarzschild case. With this correspondence, Figures 15, 16, and 17 qualitatively illustrate lensing by the Ellis wormhole. More generally, the same qualitative features occur whenever the metric function R(r) has one minimum and no other extrema, as in Figure 9.

If observer and light source are on the same side of the wormhole’s neck, and if only light rays in the asymptotic region are considered, lensing by a wormhole can be studied in terms of the quasi-Newtonian approximation formalism [182]. However, as wormholes are typically associated with negative energy densities [227, 228], the usual assumption of the quasi-Newtonian approximation formalism that the mass density is positive cannot be maintained. This observation has raised some interest in lensing by negative masses, in particular in the question of whether negative masses can be detected by their (“microlensing”) effect on the energy flux from sources passing behind them. So far, related calculations [64, 293] have been done only in the quasi-Newtonian approximation formalism.

5.5 Barriola-Vilenkin monopole

The Barriola-Vilenkin monopole [21] is given by the metric

$$g = - d{t^2} + d{r^2} + {k^2}{r^2}(d{\vartheta ^2} + {\sin ^2}\vartheta d{\varphi ^2}),$$

(115)

with a constant k < 1. There is a deficit solid angle and a singularity at r = 0; the plane t = constant, ϑ = π/2 has the geometry of a cone. (Similarly, for k > 1 one gets a surplus solid angle.) The Einstein tensor has non-vanishing components G_tt = − G_rr = (1 − k²)/r².

The metric (115) was briefly mentioned as an example for a conical singularity by Sokolov and Starobinsky [308]. Barriola and Vilenkin [21] realized that this metric can be used as a model for monopoles that might exist in the universe, resulting from breaking a global ${\mathcal O}(3)$ symmetry. They also discussed the question of whether such monopoles could be detected by their lensing properties which were characterized on the basis of some approximative assumptions (cf. [82]). However, such approximative assumptions are actually not necessary. The metric (115) has the nice property that the geodesics can be written explicitly in terms of elementary functions. This allows to write down explicit expressions for image positions and observables such as angular diameter distances, luminosity distances, image distortion, etc. (see [271]). Note that because of the deficit angle the metric (115) is not asymptotically flat in the usual sense. (It is “quasi-asymptotically flat” in the sense of [243].) For this reason, the “almost exact lens map” of Virbhadra and Ellis [337] (see Section 4.3), is not applicable to this case, at least not without modification.

The metric (115) is closely related to the metric of a static string (see metric (133) with a = 0). Restricting metric (115) to the hyperplane ϑ = π/2 and restricting metric (133) with a = 0 to the hyperplane z = constant gives the same (2 + 1)-dimensional metric. Thus, studying light rays in the equatorial plane of a Barriola-Vilenkin monopole is the same as studying light rays in a plane perpendicular to a static string. Hence, the multiple imaging properties of a Barriola-Vilenkin monopole can be deduced from the detailed discussion of the string example in Section 5.10. In particular Figures 24 and 25 show the light cone of a non-transparent and of a transparent monopole if we interpret the missing spatial dimension as circular rather than linear. This makes an important difference. While in the string case the cone of Figures 24 has a 2-dimensional set of transverse self-intersection points, the corresponding cone for the monopole has a 1-dimensional radial caustic. The difference is difficult to visualize in spacetime pictures; it is therefore recommendable to use a purely spatial visualization in terms of instantaneous wave fronts (intersections of the light cone with hypersurfaces t = constant) (compare Figures 18 and 19 with Figures 2 and 28).

Figure 18

Instantaneous wave fronts in the spacetime of a non-transparent Barriola-Vilenkin monopole with k = 0.8. The picture shows in 3-dimensional space the intersections of the past light cone of some event with four hypersurfaces t = constant, at values t₁ > t₂ > t₃ > t₄. Only one half of each instantaneous wave front and of the monopole is shown. When the wave front passes the monopole, a hole is pierced into it, then a tangential caustic develops. The caustic of each instantaneous wave front is a point, the caustic of the entire light cone is a spacelike curve in spacetime which projects to part of the axis in 3-space.

Figure 19

Instantaneous wave fronts in the spacetime of a transparent Barriola-Vilenkin monopole with k = 0.8. In addition to the tangential caustic of Figure 18 , a radial caustic is formed. For each instantaneous wave front, the radial caustic is a cusp ridge. The radial caustic of the entire light cone is a lightlike 2-surface in spacetime which projects to a rotationally symmetric 2-surface in 3-space.

5.6 Janis-Newman-Winicour spacetime

The Janis-Newman-Winicour metric [168] can be brought into the form [336]

$$g = - {\left({1 - {{2m} \over {\gamma r}}} \right)^\gamma}d{t^2} + {{d{r^2}} \over {{{\left({1 - {{2m} \over {\gamma r}}} \right)}^\gamma}}} + {{{r^2}(d{\vartheta ^2} + {{\sin}^2}\vartheta d{\varphi ^2})} \over {{{\left({1 - {{2m} \over {\gamma r}}} \right)}^{\gamma - 1}}}},$$

(116)

where m and γ are constants. It is the most general spherically symmetric static and asymptotically flat solution of Einstein’s field equation coupled to a massless scalar field. For γ = 1 it reduces to the Schwarzschild solution; in this case the scalar field vanishes. For m > 0 and γ ≠ 1, there is a naked curvature singularity at r = 2m/γ. Lensing in this spacetime was studied in [339, 338]. The main motivation was to find out whether the lensing characteristics of such a naked singularity can be distinguished from lensing by a Schwarschild black hole. The result is that the qualitative features of lensing remain similar to the Schwarzschild case as long as 1/2 < γ < 1. However, if γ drops below 1/2, they become quite different. The reason is easily understood if we write Equation (116) in the form (69). The metric coefficient

$$R(r) = r{\left({1 - {{2m} \over {\gamma r}}} \right)^{{1 \over 2} - \gamma}}$$

(117)

has a minimum between the singularity and infinity as long as ${1 \over 2} < \gamma < 1$ (see Figure 20). This minimum indicates an unstable light sphere (recall Equation (71)), as in the Schwarzschild case at r = 3m. All qualitative features of lensing carry over from the Schwarzschild case, i.e., Figures 15, 16, and 17 remain qualitatively unchanged. Clearly, the precise shape of the graph of Φ in Figure 15 changes if γ is changed. The question of how the logarithmic asymptote (“strong-field limit”) depends on γ is dicussed in [37]. If γ drops below 1/2, R(r) has no longer an extremum, i.e., there is no light sphere. This implies that only finitely many images are possible [153]. In [338] naked singularities of spherically symmetric spacetimes are called weakly naked if they are surrounded by a light sphere (cf. [59]). In a nutshell, weakly naked singularities show the same qualitative lensing features as black holes. A generalization of this result to spacetimes without spherical symmetry has not been worked out.

Figure 20

Metric coefficient R(r) for the Janis-Newman-Winicour metric. For ${1 \over 2} < \gamma < 1,R(r)$ is similar to the Schwarzschild case γ =1 (see Figure 9 ). For $\gamma \leq {1 \over 2},R(r)$ has no longer a minimum, i.e., there is no longer a light sphere which can be asymptotically approached by light rays.

5.7 Boson and fermion stars

Spherically symmetric static solutions of Einstein’s field equation coupled to a scalar field may be interpreted as (uncharged, non-rotating) boson stars if they are free of singularities. Because of the latter condition, the Wyman-Newman-Janis metric (see Section 5.6) does not describe a boson star. The theoretical concept of boson stars goes back to [179, 291]. The analogous idea of a fermion star, with the scalar field replaced by a spin 1/2 (neutrino) field, is even older [216]. Until today there is no observational evidence for the existence of either a boson or a fermion star. However, they are considered, e.g., as hypothetical candidates for supermassive objects at the center of galaxies (see [301, 324] for the boson and [335, 325] for the fermion case). For the supermassive object at the center of our own galaxy, evidence points towards a black hole, but the possibility that it is a boson or fermion star cannot be completely excluded so far.

Exact solutions that describe boson or fermion stars have been found only numerically (in 3 + 1 dimensions). For this reason there is no boson star model for which the lightlike geodesics could be studied analytically. Numerical studies of lensing have been carried out by Dabrowski and Schunck [70] for a transparent spherically symmetric static maximal boson star, and by Bilić, Nikolić, and Viollier [30] for a transparent spherically symmetric static maximal fermion star. For the case of a fermion-fermion star (two components) see [171]. In all three articles the authors use the “almost exact lens map” of Virbhadra and Ellis (see Section 4.3) which is valid for observer and light source in the asymptotic region and almost aligned. Dąbrowski and Schunck [70] also discuss how the alignment assumption can be dropped. The lensing features found in [70] for the boson star and in [30] for the fermion star have several similarities. In both cases, there is a tangential caustic and a radial caustic (recall Figure 8 for terminology). A (point) source on the tangential caustic (i.e., on the axis of symmetry through the observer) is seen as a (1-dimenional) Einstein ring plus a (point) image in the center. If the (point) source is moved away from the axis the Einstein ring breaks into two (point) images, so there are three images altogether. Two of them merge and vanish if the radial caustic is crossed. So the qualitative lensing features are quite different from a Schwarzschild black hole with (theoretically) infinitely many images (see Section 5.1). The essential difference is that in the case of a boson or fermion star there are no circular lightlike geodesics towards which light rays could asymptotically spiral.

5.8 Kerr spacetime

Next to the Schwarzschild spacetime, the Kerr spacetime is the physically most relevant example of a spacetime in which lensing can be studied explicitly in terms of the lightlike geodesics. The Kerr metric is given in Boyer-Lindquist coordinates (r, ϑ, ϕ, t) as

$$g = \varrho {(r,\vartheta)^2}\left({{{d{r^2}} \over {\Delta (r)}} + d{\vartheta ^2}} \right) + ({r^2} + {a^2}){\sin ^2}\vartheta d{\varphi ^2} - d{t^2} + {{2mr} \over {\varrho {{(r,\vartheta)}^2}}}{(a{\sin ^2}\vartheta d\varphi - dt)^2},$$

(118)

where ϱ and Δ are defined by

$$\varrho {(r,\vartheta)^2} = {r^2} + {a^2}{\cos ^2}\vartheta, \quad \Delta (r) = {r^2} - 2mr + {a^2},$$

(119)

and m and a are two real constants. We assume 0 < a < m, with the Schwarzschild case a = 0 and the extreme Kerr case a = m as limits. Then the Kerr metric describes a rotating uncharged black hole of mass m and specific angular momentum a. (The case a > m, which describes a naked singularity, will be briefly considered at the end of this section.) The domain of outer communication is the region between the (outer) horizon at

$${r_ +} = m + \sqrt {{m^2} - {a^2}}$$

(120)

and r = ∞. It is joined to the region r < r₊ in such a way that past-oriented ingoing lightlike geodesics cannot cross the horizon. Thus, for lensing by a Kerr black hole only the domain of outer communication is of interest unless one wants to study the case of an observer who has fallen into the black hole.

5.8.1 Historical notes

The Kerr metric was found by Kerr [181]. The coordinate representation (118) is due to Boyer and Lindquist [36]. The literature on lightlike (and timelike) geodesics of the Kerr metric is abundant (for an overview of the pre-1979 literature, see Sharp [306]). Detailed accounts on Kerr geodesics can be found in the books by Chandrasekhar [54] and O’Neill [248].

5.8.2 Fermat geometry

The Killing vector field ∂_t is not timelike on that part of the domain of outer communication where ϱ(r, ϑ)² ≤ 2mr. This region is known as the ergosphere. Thus, the general results of Section 4.2 on conformally stationary spacetimes apply only to the region outside the ergosphere. On this region, the Kerr metric is of the form (61), with redshift potential

$${e^{2f(r,\vartheta)}} = 1 - {{2mr} \over {\varrho{{(r,\vartheta)}^2}}},$$

(121)

Fermat metric

$$\hat g = {{\varrho{{(r,\vartheta)}^4}} \over {\varrho{{(r,\vartheta)}^2} - 2mr}}\left({{{d{r^2}} \over {\Delta (r)}} + d{\vartheta ^2}} \right) + {{\varrho{{(r,\vartheta)}^4}\Delta (r){{\sin}^2}\vartheta d{\varphi ^2}} \over {{{(\varrho{{(r,\vartheta)}^2} - 2mr)}^2}}},$$

(122)

and Fermat one-form ₂

$${\hat \phi} = {{2mra{{\sin}^2}\vartheta d\varphi} \over {\varrho{{(r,\vartheta)}^2} - 2mr}}.$$

(123)

(Equation (122) corrects a misprint in [265], Equation (66), where a square is missing.) With the Fermat geometry at hand, the optical-mechanical analogy (Fermat’s principle versus Maupertuis’ principle) allows to write the equation for light rays in the form of Newtonian mechanics (cf. [7]). Certain embedding diagrams for the Fermat geometry (optical reference geometry) of the equatorial plane have been constructed [313, 160]. However, they are less instructive than in the static case (recall Figure 11) because they do not represent the light rays as geodesics of a Riemannian manifold.

5.8.3 First integrals for lightlike geodesics

Carter [53] discovered that the geodesic equation in the Kerr metric admits another independent constant of motion K, in addition to the constants of motion L and E associated with the Killing vector fields ∂_ϕ and ∂_t. This reduces the lightlike geodesic equation to the following first-order form:

$$\varrho{(r,\vartheta)^2}\dot t = a(L - Ea{\sin ^2}\vartheta) + {{({r^2} + {a^2})(({r^2} + {a^2})E - aL} \over {\Delta (r)}},$$

(124)

$$\varrho{(r,\vartheta)^2}\dot \varphi = {{(L - Ea{{\sin}^2}\vartheta)} \over {{{\sin}^2}\varphi}} + {{({r^2} + {a^2})aE - {a^2}L} \over {\Delta (r)}},$$

(125)

$$\varrho{(r,\vartheta)^4}{\dot \varphi ^2} = K - {{{{(L - Ea{{\sin}^2}\vartheta)}^2}} \over {{{\sin}^2}\varphi}},$$

(126)

$$\varrho{(r,\vartheta)^4}{\dot r^2} = - K\Delta + {(({r^2} + {a^2})E - aL)^2}.$$

(127)

Here an overdot denotes differentiation with respect to an affine parameter s. This set of equations allows writing the lightlike geodesics in terms of elliptic integrals [16]. Clearly, ${\dot \vartheta}$ and ṙ may change sign along a ray; thus, the integration of Equation (126) and Equation (127) must be done piecewise. The determination of the turning points where ${\dot \vartheta}$ and ṙ change sign is crucial for numerical evaluation of these integrals and, thus, for ray tracing in the Kerr spacetime (see, e.g., [330, 285, 109]). With the help of Equations (126, 127) one easily verifies the following important fact. Through each point of the region

$${\mathcal K}:{(2r\Delta (r) - (r - m)\varrho{(r,\vartheta)^2})^2} \leq 4{a^2}{r^2}\Delta (r){\sin ^2}\vartheta$$

(128)

there is spherical light ray, i.e., a light ray along which r is constant (see Figure 21). These spherical light rays are unstable with respect to radial perturbations. For the spherical light ray at radius r_p the constants of motion E, L, and K satisfy

$$a{L \over E} = r_p^2 + {a^2} - {{2{r_{\rm{p}}}\Delta ({r_{\rm{p}}})} \over {{r_{\rm{p}}} - m}},$$

(129)

$${K \over {{E^2}}} = {{4r_{\rm{p}}^2\Delta ({r_{\rm{p}}})} \over {{{({r_{\rm{p}}} - m)}^2}}}.$$

(130)

The region ${\mathcal K}$ is the Kerr analogue of the “light sphere” r = 3m in the Schwarzschild spacetime.

Figure 21

The region ${\mathcal K}$, defined by Equation (128) , in the Kerr spacetime. The picture is purely spatial and shows a meridional section ϕ = constant, with the axis of symmetry at the left-hand boundary. Through each point of ${\mathcal K}$ there is a spherical geodesic. Along each of these spherical geodesics, the coordinate ϑ oscillates between extremal values, corresponding to boundary points of ${\mathcal K}$. The region ${\mathcal K}$ meets the axis at radius r_c, given by $r_{\rm{c}}^3 - 3mr_{\rm{c}}^2 + {a^2}{r_c} + m{a^2} = 0$. Its boundary intersects the equatorial plane in circles of radius $r_ + ^{{\rm{ph}}}$ (corotating circular light ray) and $r_ - ^{{\rm{ph}}}$ (counter-rotating circular light ray). $r_ \pm ^{{\rm{ph}}}$ are determined by $r_ \pm ^{{\rm{ph}}}{(r_ \pm ^{{\rm{ph}}} - 3m)^2} = 4m{a^2}$ and ${r_ +} < r_ + ^{{\rm{ph}}} < 3m < r_ - ^{{\rm{ph}}} < 4m$. In the Schwarzschild limit a → 0 the region ${\mathcal K}$ shrinks to the light sphere r = 3m. In the extreme Kerr limit a → m the region ${\mathcal K}$ extends to the horizon because in this limit both $r_ + ^{{\rm{ph}}} \rightarrow m$ and r₊ → m; for a caveat, as to geometric misinterpretations of this limit (see Figure 3 in [16]).

5.8.4 Light cone

With the help of Equations (124, 125, 126, 127), the past light cone of any observation event p_O can be explicitly written in terms of elliptic integrals. In this representation the light rays are labeled by the constants of motion L/E and K/E². In accordance with the general idea of observational coordinates (4), it is desirable to relabel them by spherical coordinates (Ψ, Θ) on the observer’s celestial sphere. This requires choosing an orthonormal tetrad (e₀, e₁, e₂, e₃) at p_O. It is convenient to choose e₁ ∝ ∂_ϑ, e₂ ∝ ∂_ϕ, e₃ ∝ ∂_r and, thus, e₀ perpendicular to the hypersurface t = constant (“zero-angular-momentum observer”). For an observation event in the equatorial plane, ϑ_O = π/2, at radius r_O, one finds

$${L \over E} = a + {{\left({({r_{\rm{O}}}(r_{\rm{O}}^2 + {a^2})\sin \Theta \sin \Psi - a{r_{\rm{O}}}\sqrt {\Delta ({r_{\rm{O}}})}} \right)} \over {{r_{\rm{O}}}\sqrt {\Delta ({r_{\rm{O}}})} + 2ma\sin \Theta \sin \Psi}},$$

(131)

$${K \over {{E^2}}} = {{r_{\rm{O}}^2\left({r_{\rm{O}}^2 + {a^2} - a{r_{\rm{O}}}\sqrt {\Delta ({r_{\rm{O}}})} \sin \Theta \sin \Psi} \right)} \over {{r_{\rm{O}}}\sqrt {\Delta ({r_{\rm{O}}})} + 2ma\sin \Theta \sin \Psi}} - {{r_{\rm{O}}^3\left({{r_{\rm{O}}}(r_{\rm{O}}^2 + {a^2}) + 2m{a^2}){{\cos}^2}\Theta} \right)} \over {{r_{\rm{O}}}\sqrt {\Delta ({r_{\rm{O}}})} + 2ma\sin \Theta \sin \Psi}}.$$

(132)

As in the Schwarzschild case, some light rays from p_O go out to infinity and some go to the horizon. In the Schwarzschild case, the borderline between the two classes corresponds to light rays that asymptotically approach the light sphere at r = 3m. In the Kerr case, it corresponds to light rays that asymptotically approach a spherical light ray in the region ${\mathcal K}$ of Figure 21. The constants of motion for such light rays are given by Equation (129, 130), with r_p varying between its extremal values $r_ + ^{{\rm{ph}}}$ and $r_ - ^{{\rm{ph}}}$ (see again Figure 21). Thereupon, Equation (131) and Equation (132) determine the celestial coordinates Ψ and Θ of those light rays that approach a spherical light ray in ${\mathcal K}$. The resulting curve on the observer’s celestial sphere gives the apparent shape of the Kerr black hole (see Figure 22). For an observation event on the axis of rotation, sin ϑ_O = 0, the Kerr light cone is rotationally symmetric. The caustic consists of infinitely many spacelike curves, as in the Schwarzschild case. A light source passing through such a caustic point is seen as an Einstein ring. For observation events not on the axis, there is no rotational symmetry and the caustic structure is quite different from the Schwarzschild case. This is somewhat disguised if one restricts to light rays in the equatorial plane ϑ = π/2 (which is possible, of course, only if the observation event is in the equatorial plane). Then the resulting 2-dimensional light cone looks indeed qualitatively similar to the Schwarzschild cone of Figure 12 (cf. [147]), where intersections of the light cone with hypersurfaces t = constant are depicted. However, in the Kerr case the transverse self-intersection of this 2-dimensional light cone does not occur on an axis of symmetry. Therefore, the caustic of the full (3-dimensional) light cone is more involved than in the Schwarzschild case. It turns out to be not a spatially straight line, as in the Schwarzschild case, but rather a tube, with astroid cross-section, that winds a certain number of times around the black hole; for a → m it approaches the horizon in an infinite spiral motion. The caustic of the Kerr light cone with vertex in the equatorial plane was numerically calculated and depicted, for a = m, by Rauch and Blandford [285]. From the study of light cones one may switch to the more general study of wave fronts. (For the definition of wave fronts see Section 2.2.) Pretorius and Israel [282] determined all axisymmetric wave fronts in the Kerr geometry. In this class, they investigated in particular those members that are asymptotic to Minkowski light cones at infinity (“quasi-spherical light cones”) and they found, rather surprisingly, that they are free of caustics.

Figure 22

Apparent shape of a Kerr black hole for an observer at radius r_O in the equatorial plane. (For the Schwarzschild analogue, see Figure 14 .) The pictures show the celestial sphere of an observer whose 4-velocity is perpendicular to a hypersurface t = constant. (If the observer is moving one has to correct for aberration.) The dashed circle is the celestial equator, Θ = π/2, and the crossing axes indicate the direction towards the center, Θ = π. Past-oriented light rays go to the horizon if their initial direction is in the black disk and to infinity otherwise. Thus, the black disk shows the part of the sky that is not illuminated by light sources at a large radius. The boundary of this disk corresponds to light rays that asymptotically approach a spherical light ray in the region ${\mathcal K}$ of Figure 21 . For an observer in the equatorial plane at infinity, the apparent shape of a Kerr black hole was correctly calculated and depicted by Bardeen [16] (cf. [54], p. 358). Earlier work by Godfrey [142] contains a mathematical error.

5.8.5 Lensing by a Kerr black hole

For an observation event p_O and a light source with worldline γ_S, both in the domain of outer communication of a Kerr black hole, several qualitative features of lensing are unchanged in comparison to the Schwarzschild case. If γ_S is past-inextendible, bounded away from the horizon and from (past lightlike) infinity, and does not meet the caustic of the past light cone of p_O, the observer sees an infinite sequence of images; for this sequence, the travel time (e.g., in terms of the time coordinate t) goes to infinity. These statements can be proven with the help of Morse theory (see Section 3.3). On the observer’s sky the sequence of images approaches the apparent boundary of the black hole which is shown in Figure 22. This follows from the fact that

• the infinite sequence of images must have an accumulation point on the observer’s sky, by compactness, and

• the lightlike geodesic with this initial direction cannot go to infinity or to the horizon, by assumption on γ_S.

If γ_S meets the caustic of p_O’s past light cone, the image is not an Einstein ring, unless p_O is on the axis of rotation. It has only an “infinitesimal” angular extension on the observer’s sky. As always when a point source meets the caustic, the ray-optical calculation gives an infinitely bright image. Numerical studies show that in the Kerr spacetime, where the caustic is a tube with astroid cross-section, the image is very bright whenever the light source is inside the tube [285]. In principle, with the lightlike geodesics given in terms of elliptic integrals, image positions on the observer’s sky can be calculated explicitly. This has been worked out for several special wordlines γ_S. The case that γ_S is a circular timelike geodesic in the equatorial plane of the extreme Kerr metric, a = m, was treated by Cunningham and Bardeen [67, 17]. This example is of relevance in view of accretion disks. Viergutz [330] developed a formalism for the case that γ_S has constant r and ϑ coordinates, i.e., for a light source that stays on a ring around the axis. One aim of this approach, which could easily be rewritten in terms of the exact lens map (recall Section 2.1), was to provide a basis for numerical studies. The case that γ_S is an integral curve of ∂_t and that γ_S and p_O are at large radii is treated by Bozza [38] under the additional assumption that source and observer are close to the equatorial plane and by Vazquez and Esteban [329] without this restriction. All these articles also calculate the brightness of images. This requires determining the cross-section of infinitesimally thin bundles with vertex, e.g., in terms of the shape parameters D₊ and D₋ (recall Figure 3). For a bundle around an arbitrary light ray in the Kerr metric, all relevant equations were worked out analytically by Pineault and Roeder [276]. However, the equations are much more involved than for the Schwarzschild case and will not be given here. Lensing by a Kerr black hole has been visualized (i) by showing the apparent distortion of a background pattern [277, 307] and (ii) by showing the visual appearence of an accretion disk [277, 281, 307]. The main difference, in comparison to the Schwarzschild case, is in the loss of the left-right symmetry. In view of observations, Kerr black holes are considered as candidates for active galactic nuclei (AGN) since many years. In particular, the X-ray variability of AGN is interpreted as coming from a “hot spot” in an accretion disk that circles around a Kerr black hole. Starting with the pioneering work in [67, 17], many articles have been written on calculating the light curves and the spectrum of such “hot spots”, as seen by a distant observer (see, e.g., [75, 12, 175, 169, 109]). The spectrum can be calculated in terms of a transfer function that was tabulated, for some values of a, in [65] (cf. [330, 331]). A Kerr black hole is also considered as the most likely candidate for the supermassive object at the center of our own galaxy. (For background material see [107].) In this case, the predicted angular diameter of the black hole on our sky, in the sense of Figure 22, is about 30 microarcseconds; this is not too far from the reach of current VLBI technologies [108]. Also, the fact that the radio emission from our galactic center is linearly polarized gives a good motivation for calculating polarimetric images as produced by a Kerr black hole The calculation is based on the geometric-optics approximation according to which the polarization vector is parallel along the light ray. In the Kerr spacetime, this parallel-transport law can be explicitly written with the help of constants of motion [61, 276, 317] (cf. [54], p. 358). As to the large number of numerical codes that have been written for calculating imaging properties of a Kerr black hole the reader may consult [176, 330, 285, 109].

5.8.5.1 Notes on Kerr naked singularities and on the Kerr-Newman spacetime

The Kerr metric with a > m describes a naked singularity and is considered as unphysical by most authors. Its lightlike geodesics have been studied in [47, 49] (cf. [54], p. 375). The Kerr-Newman spacetime (charged Kerr spacetime) is usually thought to be of little astrophysical relevance because the net charge of celestial bodies is small. For the lightlike geodesics in this spacetime the reader may consult [48, 50].

5.9 Rotating disk of dust

The stationary axisymmetric spacetime around a rigidly rotating disk of dust was first studied in terms of a numerical solution to Einstein’s field equation by Bardeen and Wagoner [18, 19]. The exact solution was found much later by Neugebauer and Meinel [236]. It is discussed, e.g., in [235]. The metric cannot be written in terms of elementary functions because it involves the solution to an ultraelliptic integral equation. It depends on a parameter μ which varies between zero and μ_c = 4.62966 …. For small μ one gets the Newtonian approximation, for μ → μ_c the extreme Kerr metric (a = m) is approached. The lightlike geodesics in this spacetime have been studied numerically and the appearance of the disk to a distant observer has been visualized [345]. It would be desirable to support these numerical results with exact statements. From the known properties of the metric, only a few qualitative lensing features of the disk can be deduced. As Minkowski spacetime is approached for μ → 0, the spacetime must be asymptotically simple and empty as long as μ is sufficiently small. (This is true, of course, only if the disk is treated as transparent.) The general results of Section 3.4 imply that in this case the gravitational field of the disk produces finitely many images of each light source, and that the number of images is odd, provided that the worldline of the light source is past-inextendible and does not go out to past lightlike infinity. For larger values of μ, this is no longer true. For μ > 0.5 there are two counter-rotating circular lightlike geodesics in the equatorial plane, a stable one at a radius ${{\tilde \rho}_1}$ inside the disk and an unstable one at a radius ${{\tilde \rho}_2}$ outside the disk. (This follows from [10] where it is shown that for μ > 0.5 timelike counter-rotating circular geodesics do not exist in a radius interval [${{\tilde \rho}_1},{{\tilde \rho}_2}$]. The boundary values of this interval give the radii of lightlike circular geodesics.) The existence of circular light rays has the consequence that the number of images must be infinite; this is obviously true if light source and observer are exactly on the spatial track of such a circular light ray and, by continuity, also in a neighborhood. For a better understanding of lensing by the disk of dust it is desirable to investigate, for each value of μ and each event p_O: Which past-oriented lightlike geodesics that issue from p_O go out to infinity and which are trapped? Also, it is desirable to study the light cones and their caustics.

5.10 Straight spinning string

Cosmic strings (and other topological defects) are expected to exist in the universe, resulting from a phase transition in the early universe (see, e.g., [334] for a detailed account). So far, there is no direct observational evidence for the existence of strings. In principle, they could be detected by their lensing effect (see [295] for observations of a recent candidate and [164] for a discussion of the general perspective). Basic lensing features for various string configurations are briefly summarized in [9]. Here we consider the simple case of a straight string that is isolated from all other masses. This is one of the most attractive examples for investigating lensing from the spacetime perspective without approximations. In particular, studying the light cones in this metric is an instructive exercise. The geodesic equation is completely integrable, and the geodesics can even be written explicitly in terms of elementary functions.

We consider the spacetime metric

$$g = - {(dt - ad\varphi)^2} + d{z^2} + d{\rho ^2} + {k^2}{\rho ^2}d{\varphi ^2},$$

(133)

with constants a and k > 0. As usual, the azimuthal coordinate ϕ is defined modulo 2π. For a = 0 and k = 1, metric (133) is the Minkowski metric in cylindrical coordinates. For any other values of a and k, the metric is still (locally) flat but not globally isometric to Minkowski spacetime; there is a singularity along the z-axis. For a = 0 and 0 < k < 1, the plane t = constant, z = constant has the geometry of a cone with a deficit angle

$$\delta = (1 - k)2\pi.$$

(134)

(see Figure 23); for k > 1 there is a surplus angle. Note that restricting the metric (133) with a = 0 to the hyperplane z = constant gives the same result as restricting the metric (115) of the Barriola-Vilenkin monopole to the hyperplane ϑ = π/2.

Figure 23

On a cone with deficit angle 0 < δ < π, the point p can be connected to every point q in the double-imaging region (shaded) by two geodesics and to a point in the single-imaging region (non-shaded) by one geodesic.

The metric (133) describes the spacetime around a straight spinning string. The constant k is related to the string’s mass-per-length μ, in Planck units, via

$$k = 1 - 4\mu,$$

(135)

whereas the constant a is a measure for the string’s spin. Equation (135) shows that we have to restrict to the deficit-angle case k < 1 to have μ non-negative. One may treat the string as a line singularity, i.e., consider the metric (133) for all ρ > 0. (This “wire approximation”, where the energy-momentum tensor of the string is concentrated on a 2-dimensional submanifold, is mathematically delicate; see [135].) For a string of finite radius ρ_* one has to match the metric (133) at ρ = ρ_* to an interior solution, thereby getting a metric that is regular on all of ℝ⁴.

5.10.1 Historical notes

With a = 0, the metric (133) and its geodesics were first studied by Marder [213, 214]. He also discussed the matching to an interior solution, without, however, associating it with strings (which were no issue at that time). The same metric was investigated by Sokolov and Starobinsky [308] as an example for a conic singularity. Later Vilenkin [332, 333] showed that within the linearized Einstein theory the metric (133) with a = 0 describes the spacetime outside a straight non-spinning string. Hiscock [159], Gott [144], and Linet [207] realized that the same is true in the full (non-linear) Einstein theory. Basic features of lensing by a non-spinning string were found by Vilenkin [333] and Gott [144]. The matching to an interior solution for a spinning string, a ≠ 0, was worked out by Jensen and Soleng [170]. Already earlier, the restriction of the metric (133) with a ≠ 0 to the hyperplane z = 0 was studied as the spacetime of a spinning particle in 2 + 1 dimensions by Deser, Jackiw, and’ t Hooft [77]. The geodesics in this (2+ 1)-dimensional metric were first investigated by Clément [60] (cf. Krori, Goswami, and Das [192] for the (3 + 1)-dimensional case). For geodesics in string metrics one may also consult Galtsov and Masar [131]. The metric (133) can be generalized to the case of several parallel strings (see Letelier [205] for the non-spinning case, and Krori, Goswami, and Das [192] for the spinning case). Clarke, Ellis and Vickers [58] found obstructions against embedding a string model close to metric (133) into an almost-Robertson-Walker spacetime. This is a caveat, indicating that the lensing properties of “real” cosmic strings might be significantly different from the lensing properties of the metric (133).

5.10.2 Redshift and Fermat geometry

The string metric (133) is stationary, so the results of Section 4.2 apply. Comparison of metric (133) with metric (61) shows that the redshift potential vanishes, f = 0. Hence, observers on t-lines see each other without redshift. The Fermat metric ${\hat g}$ and Fermat one-form ${\hat \phi}$ read

$$\hat g = d{z^2} + d{\rho ^2} + {k^2}{\rho ^2}d{\varphi ^2},$$

(136)

$$\hat g = d{z^2} + d{\rho ^2} + {k^2}{\rho ^2}d{\varphi ^2},$$

(137)

As the Fermat one-form is closed, $d\hat \phi = 0$, the spatial paths of light rays are the geodesics of the Fermat metric ${\hat g}$ (cf. Equation (64)), i.e., they are not affected by the spin of the string. ${\hat \phi}$ can be transformed to zero by changing from t to the new time function t − aϕ. Then the influence of the string’s spin on the travel time (62) vanishes as well. However, the new time function is not globally well-behaved (if a ≠ 0), because ϕ is either discontinuous or multi-valued on any region that contains a full circle around the z-axis. As a consequence, ${\hat \phi}$ can be transformed to zero on every region that does not contain a full circle around the z-axis, but not globally. This may be viewed as a gravitational analogue of the Aharonov-Bohm effect (cf. [309]). The Fermat metric (136) describes the product of a cone with the z-line. Its geodesics (spatial paths of light rays) are straight lines if we cut the cone open and flatten it out into a plane (see Figure 23). The metric of a cone is (locally) flat but not (globally) Euclidean. This gives rise to another analogue of the Aharonov-Bohm effect, to be distinguished from the one mentioned above, which was discussed, e.g., in [115, 29, 155].

5.10.3 Light cone

For the metric (133), the lightlike geodesics can be explicitly written in terms of elementary functions. One just has to apply the coordinate transformation (t, ϕ) ↦ (t − aϕ, kϕ) to the lightlike geodesics in Minkowski spacetime. As indicated above, the new coordinates are not globally well-behaved on the entire spacetime. However, they can be chosen as continuous and single-valued functions of the affine parameter s along all lightlike geodesics through some chosen event, with ϕ taking values in ℝ. In this way we get the following representation of the lightlike geodesics that issue from the observation event (ρ = ρ₀, ϕ = 0, z = 0, t = 0) into the past:

$$\rho (s) = \sqrt {{s^2}{{\sin}^2}\Theta + 2{\rm{s}}{\rho _0}\sin \Theta \cos \Psi + \rho _0^2},$$

(138)

$$\tan (k\varphi (s)) = {{s\sin \Theta \sin \Psi} \over {{\rho _0} + s\sin \Theta \cos \Psi}},$$

(139)

$$z(s) = s\cos \Theta,$$

(140)

$$t(s) = - s + a\varphi (s).$$

(141)

The affine parameter s coincides with ${\hat g}$-arclength ℓ, and (Ψ, Θ) parametrize the observer’s celestial sphere,

$${d \over {ds}}{\left. {\left({\begin{array}{*{20}c} {\rho (s)\cos \varphi (s)} \\ {\rho (s)\sin \varphi (s)} \\ {z(s)} \\ \end{array}} \right)} \right\vert _{s = 0}} = \left({\begin{array}{*{20}c}{\cos \Psi \sin \Theta} \\ {\sin \Psi \sin \Theta} \\ {\cos \Theta} \\ \end{array}} \right).$$

(142)

Equations (138, 139, 140, 141) give us the light cone parametrized by (s, Θ, Ψ)The same equations determine the intersection of the light cone with any timelike hypersurface (source surface) and thereby the exact lens map in the sense of Frittelli and Newman [123] (recall Section 2.1). For k = 0.8 and a = 0, the light cone is depicted in Figure 24; intersections of the light cone with hypersurfaces t = constant (“instantaneous wave fronts”) are shown in Figure 27. In both pictures we consider a non-transparent string of finite radius ρ_*, i.e., the light rays terminate if they meet the boundary of the string. Figures 25 and 28 show how the light cone is modified if the string is transparent. This requires matching the metric (133) to an interior solution which is everywhere regular and letting light rays pass through the interior. For the non-transparent string, the light cone cannot form a caustic, because the metric is flat. For the transparent string, light rays that pass through the interior of the string do form a caustic. The special form of the interior metric is not relevant. The caustic has the same features for all interior metrics that monotonously interpolate between a regular axis and the boundary of the string. Also, there is no qualitative change of the light cone for a spinning string as long as the spin a is small. Large values of a, however, change the picture drastically. For ${a^2} > {k^2}\rho _*^2$, where ρ_* is the radius of the string, the ϕ-lines become timelike on a neighborhood of the string. As the ϕ-lines are closed, this indicates causality violation. In this causality-violating region the hypersurfaces t = constant are not everywhere spacelike and, in particular, not transverse to all lightlike geodesics. Thus, our notion of instantaneous wave fronts becomes pathological.

Figure 24

Past light cone of an event p_O in the spacetime of a non-transparent string of finite radius with k = 0.8 and a = 0. The metric (133) is considered on the region ρ > ρ_*, and the light rays are cut if they meet the boundary of this region. The z coordinate is not shown, the vertical coordinate is time t. The “chimney” indicates the region ρ < pρ_* which is occupied by the string. The light cone has no caustic but a transverse self-intersection (cut locus). The cut locus, in the (2 + 1)-dimensional picture represented as a curve, is actually a 2-dimensional spacelike submanifold. When passing through the cut locus, the lightlike geodesics leave the boundary of the chronological past I⁻(p_O). Note that the light cone is not a closed subset of the spacetime.

Figure 25

Past light cone of an event p_O in the spacetime of a transparent string of finite radius ρ_* with k = 0.8 and a = 0. The metric (133) is matched at ρ = ρ_* to an interior metric, and light rays are allowed to pass through the interior region. The perspective is analogous to Figure 24 . The light rays which were blocked by the string in the non-transparent case now form a caustic. In the (2 + 1)-dimensional picture the caustic consists of two lightlike curves that meet in a swallow-tail point (see Figure 26 for a close-up). Taking the z-dimension into account, the caustic actually consists of two lightlike 2-manifolds (fold surfaces) that meet in a spacelike curve (cusp ridge). The third picture in Figure 2 shows the situation projected to 3-space. Each of the past-oriented lightlike geodesics that form the caustic first passes through the cut locus (transverse self-intersection), then smoothly slips over one of the fold surfaces. The fold surfaces are inside the chronological past I⁻(p_O), the cusp ridge is on its boundary.

Figure 26

Close-up of the caustic of Figure 25 . The string is not shown. Taking the z-dimension into account, the swallow-tail point is actually a spacelike curve (cusp ridge).

Figure 27

Instantaneous wave fronts in the spacetime of a non-transparent string of finite radius ρ* with k = 0.8 and a = 0. The picture shows in 3-dimensional space the intersections of the light cone of Figure 24 with three hypersurfaces t = constant, at values t₁ > t₂ > t₃. The vertical coordinate is the z-coordinate which was suppressed in Figure 24 . Only one half of each instantaneous wave front is shown so that one can look into its interior. There is a transverse self-intersection (cut locus) but no caustic.

Figure 28

Instantaneous wave fronts in the spacetime of a transparent string of finite radius ρ_* with k = 0.8 and a = 0. The picture is related to Figure 25 as Figure 27 is related to Figure 24 . Instantaneous wave fronts that have passed through the string have a caustic, consisting of two cusp ridges that meet in a swallow-tail point. This caustic is stable (see Section 2.2 ). The caustic of the light cone in Figure 25 is the union of the caustics of its instantaneous wave fronts. It consists of two fold surfaces that meet in a cusp ridge, like in the third picture of Figure 2 .

5.10.4 Lensing by a non-transparent string

With the lightlike geodesics known in terms of elementary functions, positions and properties of images can be explicitly determined without approximation. We place the observation event at ρ = ρ₀, ϕ = 0, z = 0, t = 0, and we consider a light source whose worldline is a t-line at ρ = ρ_S, ϕ = ϕ_S, z = z_S with 0 ≤ ϕ_S ≤ π. From Equations (138, 139, 140) we find that the images are in one-to-one correspondence with integers n such that

$$\vert {\varphi _{\rm{S}}} + 2n\pi \vert < \pi/k.$$

(143)

They can be numbered by the winding number n in the order n = 0, −1, 1, −2, 2, … The total number of images depends on k. Let N₁(k) be the largest integer and N₂(k) be the smallest integer such that N₁(k) ≤ 1/k < N₂(k). Of the two integers N₁(k) and N₂(k), denote the odd one by N_odd(k) and the even one by N_even(k). Then we find from Equation (143)

$$0 \leq {\varphi _{\rm{S}}} < \vert {N_{{\rm{even}}}} - 1/k\vert \pi:\quad {N_{{\rm{odd}}}}(k){\rm{images}},$$

(144)

$$\vert {N_{{\rm{even}}}} - 1/k\vert \pi < {\varphi _{\rm{S}}} \leq \pi:\quad {{\rm N}_{{\rm{even}}}}(k){\rm{images}}.$$

(145)

Thus, the number of images is even in a wedge-shaped region behind the string and odd everywhere else. If the light source approaches the boundary between the two regions, one image vanishes behind the string (see Figure 23 for the case 1 < 1/k < 2). (If the non-transparent string has finite thickness, there is also a region with no image at all, in the “shadow” of the string.) The coordinates (Ψ_n, Θ_n) on the observer’s sky of an image with winding number n and the affine parameter s_n at which the light source is met can be determined from Equations (138, 139, 140). We just have to insert $\rho (s) = {\rho _{\rm{S}}},\varphi (s) = {\varphi _{\rm{S}}} + 2n\pi, z(s) = {z_{\rm{S}}}$ and to solve for tanΨ = tanΨ_n tanΘ = tanΘ_n s = s_n:

$$\tan {\Psi _n} = {{{\rho _{\rm{S}}}\sin (k({\varphi _{\rm{S}}} + 2n\pi))} \over {{\rho _{\rm{S}}}\cos (k({\varphi _{\rm{S}}} + 2n\pi)) - {\rho _0}}},$$

(146)

$$\tan {\Theta _n} = {{\sqrt {\rho _{\rm{S}}^2 + \rho _0^2 - 2\rho {\rm{S}}{\rho _0}\cos (k({\varphi _{\rm{S}}} + 2n\pi))}} \over {{z_{\rm{S}}}}},$$

(147)

$${s_n} = \sqrt {z_{\rm{S}}^2 + \rho _{\rm{S}}^2 + \rho _0^2 - 2{\rho _{\rm{S}}}{\rho _0}\cos (k({\varphi _{\rm{S}}} + 2n\pi))}.$$

(148)

The travel time follows from Equation (141):

$${T_n} = {s_n} - a({\varphi _{\rm{S}}} + 2n\pi).$$

(149)

It is the only relevant quantity that depends on the string’s spin a. With the observer on a t-line, the affine parameter s coincides with the area distance, D_area(s) = s, because in the (locally) flat string spacetime the focusing equation (44) reduces to D_area = 0. For observer and light source on t-lines, the redshift vanishes, so s also coincides with the luminosity distance, D_lum(s) = s, owing to the general law (48). Hence, Equation (148) gives us the brightness of images (see Section 2.6 for the relevant formulas). The string metric produces no image distortion because the curvature tensor (and thus, the Weyl tensor) vanishes (recall Section 2.5). Realistic string models yield a mass density μ that is smaller than 10⁻⁴. So, by Equation (135), only the case N_odd(k) = 1 and N_even(k) = 2 is thought to be of astrophysical relevance. In that case we have a single-imaging region, 0 ≤ ϕ_S < 2π − π/k, and a double-imaging region, 2π − π/k < ϕ_S ≤ π (see Figure 23). The occurrence of double-imaging and of single imaging can also be read from Figure 24. In the double-imaging region we have a (“primary”) image with n = 0 and a (“secondary”) image with n = −1. From Equations (147, 148) we read that the two images have different latitudes and different brightnesses. However, for k close to 1 the difference is small. If we express k by Equation (134) and linearize Equations (146, 147, 148, 149) with respect to the deficit angle (134), we find

$${T_n} = {s_n} - a({\varphi _{\rm{S}}} + 2n\pi).$$

(150)

$${\Psi _{- 1}} = {\Psi _0} + {{{\rho _{\rm{S}}}\delta} \over {{\rho _{\rm{S}}} + {\rho _0}}},$$

(151)

$${\Theta _{- 1}} - {\Theta _0} = 0,$$

(152)

$${s_{- 1}} - {s_0} = 0,$$

(153)

$${T_{- 1}} - {T_0} = 2a\pi.$$

(154)

Hence, in this approximation the two images have the same Θ−coordinate; their angular distance Δ on the sky is given by Vilenkin’s [333] formula

$$\Delta = {{{\rho _{\rm{S}}}\delta \sin {\Theta _0}} \over {{\rho _{\rm{S}}} + {\rho _0}}},$$

(155)

and is thus independent of ϕ_S; they have equal brightness and their time delay is given by the string’s spin a via Equation (154). All these results apply to the case that the worldlines of the observer and of the light source are t-lines. Otherwise redshift factors must be added.

5.10.5 Lensing by a transparent string

In comparison to a non-transparent string, a transparent string produces additional images. These additional images correspond to light rays that pass through the string. We consider the case a = 0 and 1 < 1/k < 2, which is illustrated by Figures 24 and 25. The general features do not depend on the form of the interior metric, as long as it monotonously interpolates between a regular axis and the boundary of the string. In the non-transparent case, there is a single-imaging region and a double-imaging region. In the transparent case, the double-imaging region becomes a triple-imaging region. The additional image corresponds to a light ray that passes through the interior of the string and then smoothly slips over one of the cusp ridges. The point where this light ray meets the worldline of the light source is on the sheet of the light cone between the two cusp ridges in Figure 25, i.e., on the sheet that does not exist in the non-transparent case of Figure 24. From the picture it is obvious that the additional image shows the light source at a younger age than the other two images (so it is a “tertiary image”). A light source whose worldline meets the caustic of the observer’s past light cone is on the borderline between single-imaging and triple-imaging. In this case the tertiary image coincides with the secondary image and it is particularly bright (even infinitely bright according to the ray-optical treatment; recall Section 2.6). Under a small perturbation of the worldline the bright image either splits into two or vanishes, so one is left either with three images or with one image.

5.11 Plane gravitational waves

A plane gravitational wave is a spacetime with metric

$$g = - 2dudv - (f(u)({x^2} - {y^2}) + 2g(u)xy)d{y^2} + d{x^2} + d{y^2},$$

(156)

where f(u)² + g(u)² is not identically zero. For any choice of f(u) and g(u), the metric (156) has vanishing Ricci tensor, i.e., Einstein’s vacuum field equation is satisfied. The lightlike vector field ∂_v is covariantly constant. Non-flat spacetimes with a covariantly constant lightlike vector field are called plane-fronted waves with parallel rays or pp-waves for short. They made their first appearance in a purely mathematical study by Brinkmann [43].

In spite of their high idealization, plane gravitational waves are interesting mathematical models for studying the lensing effect of gravitational waves. In particular, the focusing effect of plane gravitational waves on light rays can be studied quite explicitly, without any weak-field or small-angle approximations. This focusing effect is reflected by an interesting light cone structure.

The basic features with relevance to lensing can be summarized in the following way. If the profile functions f and g are differentiable, and the coordinates (x, y, u, v) range over ℝ⁴, the spacetime with the metric (156) is geodesically complete [92]. With the exception of the integral curves of ∂_v, all inextendible lightlike geodesics contain a pair of conjugate points. Let q be the first conjugate point along a past-oriented lightlike geodesic from an observation event p_O. Then the first caustic of the past light cone of p_O is a parabola through q. (It depends on the profile functions f and g whether or not there are more caustics, i.e., second, third, etc. conjugate points.) This parabola is completely contained in a hyperplane u = constant. All light rays through p_O, with the exception of the integral curve of ∂_v, pass through this parabola. In other words, the entire sky of p_O, with the exception of one point, is focused into a curve (see Figure 29). This astigmatic focusing effect of plane gravitational waves was discovered by Penrose [259] who worked out the details for “sufficiently weak sandwich waves”. (The name “sandwich wave” refers to the case that f(u) and g(u) are different from zero only in a finite interval u₁ < u < u₂.) Full proofs of the above statements, for arbitrary profile functions f and g, were given by Ehrlich and Emch [94, 95] (cf. [25], Chapter 13). The latter authors also demonstrate that plane gravitational wave spacetimes are causally continuous but not causally simple. This strengthens Penrose’s observation [259] that they are not globally hyperbolic. (For the hierarchy of causality notions see [25].) The generators of the light cone leave the boundary of the chronological past I⁻(p_O) when they reach the caustic. Thus, the above-mentioned parabola is also the cut locus of the past light cone. By the general results of Section 2.8, the occurrence of a cut locus implies that there is multiple imaging in the plane-wave spacetime. The number of images depends on the profile functions. We may choose the profile functions such that there is no second caustic. (The “sufficiently weak sandwich waves” considered by Penrose [259] are of this kind.) Then Figure 29 demonstrates that an appropriately placed worldline (close to the caustic) intersects the past light cone exactly twice, so there is double-imaging. Thus, the plane waves demonstrate that the number of images need not be odd, even in the case of a geodesically complete spacetime with trivial topology.

Figure 29

Past light cone of an event p_O in the spacetime (156) of a plane gravitational wave. The picture was produced with profile functions f(u) > 0 and g(u) = 0. Then there is focusing in the x-direction and defocusing in the y-direction. In the (2 + 1)-dimensional picture, with the y-coordinate not shown, the past light cone is completely refocused into a single point q, with the exception of one generator λ. It depends on the profile functions whether there is a second, third, and so on, caustic. In any case, the generators leave the boundary of the chronological past I⁻(p_O) when they pass through the first caustic. Taking the y-coordinate into account, the first caustic is not a point but a parabola (“astigmatic focusing”) (see Figure 30 ). An electromagnetic plane wave (vanishing Weyl tensor rather than vanishing Ricci tensor) can refocus a light cone, with the exception of one generator, even into a point in 3 + 1 dimensions (“anastigmatic focusing”) (cf. Penrose [259] where a hand-drawing similar to the picture above can be found).

Figure 30

“Small wave fronts” of the light cone in the spacetime (156) of a plane gravitational wave. The picture shows the intersection of the light cone of Figure 29 with the lightlike hyperplane u = constant for three different values of the constant: (a) exactly at the caustic (parabola), (b) at a larger value of u (hyperbolic paraboloid), and (c) at a smaller value of u (elliptic paraboloid). In each case, the hyperplane u = constant does not intersect the one generator λ tangent to ∂_v; all other generators are intersected transversely and exactly once.

The geodesic and causal structure of plane gravitational waves and, more generally, of pp-waves is also studied in [163, 51].

One often considers profile functions f and g with Dirac-delta-like singularities (“impulsive gravitational waves”). Then a mathematically rigorous treatment of the geodesic equation, and of the geodesic deviation equation, is delicate because it involves operations on distributions which are not obviously well-defined. For a detailed mathematical study of this situation see [310, 193].

Garfinkle [132] discovered an interesting example for a pp-wave which is singular on a 2-dimensional worldsheet. This exact solution of Einstein’s vacuum field equation can be interpreted as a wave that travels along a cosmic string. Lensing in this spacetime was numerically discussed by Vollick and Unruh [340].

The vast majority of work on lensing by gravitational waves is done in the weak-field approximation. For the exact treatment and in the weak-field approximation one may use Kovner’s version of Fermat’s principle (see Section 2.9), which has the advantage that it allows for time-dependent situations. Applications of this principle to gravitational waves have been worked out in the original article by Kovner [187] and by Faraoni [110, 111].