The impurity size-effect and phonon deformation potentials in wurtzite GaN

Empirically, the size effect is usually described by a parameter $\beta_\mathrm{size}$ which multiplies by the concentration of impurities $N_\mathrm{D}$ to the normalized lattice parameter change Δa/a

$$\begin{equation} \frac{\Delta a}{a} = \beta_\mathrm{size} N_\mathrm{D}. \end{equation} \tag{ 1 }$$

A similar relation for the electronic contribution of free carriers via the deformation potential change is

$$\begin{equation} \frac{\Delta a}{a} = \beta_{e} n, \end{equation} \tag{ 2 }$$

where n is the free-electron concentration. It is obvious, that different donors are described by different $\beta_\mathrm{size}$, while the deformation potential effect of electrons is independent on the donor species. Romano and colleagues [6], report $\beta_\mathrm{Si} = -1.6\times 10^{-24}\ \mathrm{cm^3}$, Van de Walle (who also coauthors the Romano et al study) presents a value of $\beta_\mathrm{Si} = -2.6\times 10^{-24}\ \mathrm{cm^3}$ three years later [2]. Following the ideas of Cargill et al [15] we estimate $\beta_\mathrm{size}$ from the relative relaxation of neighboring atoms when introducing an impurity. These atomic relaxations are reported in reference [4] for Si and Ge in GaN and can be converted to $\beta_\mathrm{Si} = -1.7\times 10^{-24}\ \mathrm{cm^3}$ and $\beta_\mathrm{Ge} = -0.4\times 10^{-24}\ \mathrm{cm^3}$, respectively.

The strength of the electronic effect described by β_e in equation (2) is estimated by

$$\begin{equation} \beta_e = -\frac{a_c}{3B}. \end{equation} \tag{ 3 }$$

Here, a_c is the deformation potential of the conduction band and B the bulk modulus of GaN which is given by the elastic constants C_ij as

$$\begin{equation} B = \frac{C_{33}\left(C_{11}+C_{12}\right)-2C_{13}^2}{C_{11}+C_{12}+2C_{33}-4C_{13}}. \end{equation} \tag{ 4 }$$

Depending on the choice of elastic constants $B = \left( 210\ \pm\ 20\right)\ \mathrm{GPa}$. However, for a_c very different results are reported yielding consequently very different values for β_e. References [2, 6] both use $\beta_e = 1.5\times 10^{-24}\ \mathrm{cm^3}$ ($a_c = -6\ \mathrm{eV}$ and $B = 210\ \mathrm{GPa}$). We note, that for a_c values between $-6\ \mathrm{eV}$ [17], $\approx -9\ \mathrm{eV}$ [18] and even $-13\ \mathrm{eV}$ [19] are discussed. Embracing also the full range of B, we consequently estimate $1.4\times 10^{-24}\ \mathrm{cm^3}<\beta_e<3.6\times 10^{-24}\ \mathrm{cm^3}$. Nevertheless, it is clear that β_e > 0, while $\beta_\mathrm{size}<0$ for both donor species. Furthermore, all values for β are of the same order of magnitude, therefore the electronic and the size-effect will cancel each other out, at least partially. If we now assume $n = N_\mathrm{D}$, i.e. full donor ionization with no additional donors or compensating acceptors, we can simply add the effects up:

$$\begin{equation} \beta_{tot} = \beta_e+\beta_\mathrm{size.} \end{equation} \tag{ 5 }$$

In case of Si, β_tot is therefore expected in the interval between −1.2 × 10⁻²⁴ and $+2.0 \times 10^{-24}\ \mathrm{cm^3}$. For Ge, this range is from +1.0 × 10⁻²⁴ to $+3.2 \times 10^{-24}\ \mathrm{cm^3}$. We want to emphasize that these values are composed from different literature reports. A comparison of different sources and our results in comparison is provided at the end of this article in table 2. Considering a very high but still realistic doping level of $n = N_\mathrm{D} = 1\times 10^{20}\ \mathrm{cm^{-3}}$, we end up with a strain between $\epsilon = \Delta a/a = -1.2\times 10^{-4}$ and 3.2 × 10⁻⁴. Thus, the sign of the total effect is still unclear and it may even be zero by chance.

For epitaxial samples, the strongest contribution to strain will usually arise from epitaxial strain, i.e. thermal and lattice mismatch to substrate material or template. The a-plane thin film samples investigated here have average strain values of the order of 10⁻³ [20]. Therefore, we have to control the epitaxial strain with very high accuracy when we want to make any claims about the influence of the size effect. Consequently, we look upon all three orthogonal lattice parameters of our samples. The definition of strain values requires definition of strain-free lattice parameters of the ideal crystal. Here, we adopt the values from reference [21], where

$$\begin{align} a_0 & = 3.189\,26\ \unicode{8491},\nonumber \\ c_0 & = 5.185\,23\ \unicode{8491}. \end{align} \tag{ 6 }$$

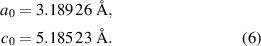
For the lattice parameter in m-direction, the geometrical identity $m_0 = \frac{\sqrt{3}}{2}a_0 = 2.761\,98\ \unicode{8491}$ is used. The experimentally found strain is consequently defined as

$$\begin{align} \epsilon_{a} & = \frac{a}{a_0}-1,\nonumber\\ \epsilon_{c} & = \frac{c}{c_0}-1,\\ \epsilon_{m} & = \frac{m}{m_0}-1.\nonumber \end{align} \tag{ 7 }$$

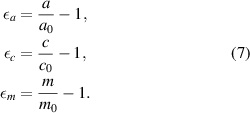
Here, we develop a simple model for the strain of doped GaN taking into account both the impurity effect and the epitaxial strain effect. We exemplarily present it for the lattice parameter a but it is identical for c or m of course. We assume that the unstrained lattice parameters given in equation (6) are valid for the undoped case, i.e. $n = N_\mathrm{D}\rightarrow 0$ which is in line with the goal of reference [21]. We consequently assign any doped sample an altered a₀(n), dependent on the dopant concentration

$$\begin{equation} a_0(n) = a_0(n = 0)\left( 1 + \beta_{tot} n\right), \end{equation} \tag{ 8 }$$

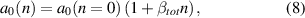
where a₀(n = 0) is a₀ from equation (6). Our samples are grown in the a-direction, this means in Hooke's law no force may be present in a-direction at the sample surface. In σ =  C, the out-of-plane stress component must vanish:

$$\begin{equation} \sigma_a = C_{11}\epsilon_a + C_{12} \epsilon_m + C_{13} \epsilon_c = 0. \end{equation} \tag{ 9 }$$

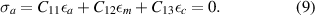
Putting equations (7) and (8) into equation (9), we obtain for β_tot

$$\begin{equation} \beta_{tot} = \frac{1}{n} \left( \frac{C_{11}\frac{a}{a_0}+C_{12}\frac{m}{m_0}+C_{13}\frac{c}{c_0}}{C_{11} +C_{12}+C_{13} }-1 \right). \end{equation} \tag{ 10 }$$

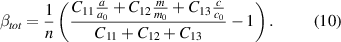
For a given (and carrier concentration independent) set of elastic constants, only experimental lattice parameters (a, m, and c) and the carrier concentration $n = N_\mathrm{D}$ have to be known to obtain β_tot. Of course, equation (10) describes the situation for every donor species separately. As we investigate the donors Si and Ge, we obtain two different β_tot whose difference Δβ exactly resembles the difference in $\beta_\mathrm{size}$ between both donor species.

As control experiments to verify our results independently, we find infrared spectroscopic ellipsometry data and Raman spectra very helpful. In the case of GaN, A₁ and E₁ transverse optical phonons are both infrared and Raman active and can thus be observed by both techniques. Furthermore, the infrared dielectric function yields the plasma frequency $\omega_\mathrm{P}$ which is directly related to the free carrier concentration n and is therefore very useful to verify the Hall effect data. The same dielectric function shows up in Raman spectra as loss function. The dielectric functions of these samples were used before to investigate the carrier dependent effective electron masses of GaN [22], the valence band dispersion [20], and the energy separation of Γ and L-points [23].

Changed lattice parameters influence the phonon eigenenergies. The interrelation is usually described by phonon deformation potentials [24]. For A₁ phonons, the energy shift is given by

$$\begin{equation} \Delta \omega_{\mathrm{A}_1} = a_{\mathrm{A}_1} \left( \epsilon_a + \epsilon_m \right) + b_{\mathrm{A}_1} \epsilon_c, \end{equation} \tag{ 11 }$$

with the phonon deformation potentials $a_{\mathrm{A}_1}$ and $b_{\mathrm{A}_1}$. For E₁ phonons (and similarly for the only Raman-active E₂ phonons) this equation reads

$$\begin{equation} \Delta \omega_{\mathrm{E}_1} = a_{\mathrm{E}_1} \left( \epsilon_a + \epsilon_m \right) + b_{\mathrm{E}_1} \epsilon_c \pm c_{\mathrm{E}_1} \left|\epsilon_a -\epsilon_m \right|, \end{equation} \tag{ 12 }$$

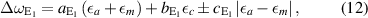
neglecting shear strain which is justified for a-oriented material. E₁ phonons are more complicated to describe because of the occurrence of the additional phonon deformation potential $c_{\mathrm{E}_1}$.

In the literature, different sets of phonon deformation potentials $a_{\mathrm{A}_1}$, $b_{\mathrm{A}_1}$, $a_{\mathrm{E}_1}$, $b_{\mathrm{E}_1}$, and $a_{\mathrm{E}_2}$, $b_{\mathrm{E}_2}$ are reported, however for $c_{\mathrm{E}_1}$ (and for $c_{\mathrm{E}^h_2}$) we could find only one report. In table 1 these results are collected. Obviously, the experimental values tabulated here for a and b agree rather well with each other for all three phonons considered.

Table 1. Phonon deformation potentials (in $\mathrm{cm^{-1}}$) as reported in the literature for the considered phonon modes in GaN.

	A1	E1	E$^h_2$
a	−630 ± 40a	−820 ± 25a	−850 ± 25a
	−640b	−717b	−742b
	−664 ± 129d		−850 ± 177c
	−681 ± 64e	−854 ± 50e	−911 ± 54e
b	−1290 ± 80a	−680 ± 50a	−920 ± 60a
	−695b	−591b	−715b
	−1182 ± 282d		−963 ± 220c
	−1067 ± 73e	−780 ± 70e	−852 ± 76e
$\left| c \right|$		379 ± 43d	379 ± 107d
		184 ± 80f	65 ± 20f

^a Reference [25], Raman spectroscopy ^b Reference [24], theory ^c Reference [26], Raman spectroscopy ^d Reference [27], Raman spectrocopy and IRSE ^e Reference [28], Raman spectroscopy ^fThis work

To connect equations (11) and (12) with experimental phonon energies ω, a strain-free eigenenergy of the respective phonon mode ω₀ = ω − Δω has to be known with relatively high accuracy to avoid propagation errors in the phonon deformation potential analysis. Therefore, we investigated a strain-free a-plane cut of a free-standing GaN crystal grown by hydride vapor phase epitaxy commercially obtained from Kyma Technologies, Raleigh, as a reference first. The values for ω₀ at room temperature agree well with experimental reports from the literature [29–34]. Specifically, we use $\omega_{0,\mathrm{A_1}} = 531.4\ \mathrm{cm^{-1}}$, $\omega_{0,\mathrm{E_1}} = 558.6\ \mathrm{cm^{-1}}$, and $\omega_{0,\mathrm{E^h_2}} = 567.4\ \mathrm{cm^{-1}}$.

The experimentally determined lattice parameters for all three axis are shown in figure 1 as a function of free electron concentration n as determined by Hall effect measurements. While a and m lattice parameters remain approximately constant as a function of n, the c lattice parameter increases as a function of electron concentration from about $5.175\ \unicode{8491}$ at low doping up to $5.180\ \unicode{8491}$ at $\approx10^{20}\ \mathrm{cm^{-3}}$. Clearly, these experimental results violate equation (9) if the elastic constants C₁₁, C₁₂, and C₁₃ and the reference lattice parameters a₀, m₀, and c₀ are constant, i.e. free electron concentration independent.

Zoom In Zoom Out Reset image size

We visualize this fact by computing the residual out-of-plane stress σ_a by equation (9) as a function of n (figure 2). For the two different donor species, separate linear fits are applied and drawn as well. We want to stress that this nonzero n-dependent stress is not real. In contrast, we use σ_a≠ 0 to show the carrier concentration dependent effect which is very obvious in our data and which we identify as the impurity-size effect. The difference between doping by Ge and by Si is likely to be identified by the different ionic radii of the dopant cores replacing Ga in the GaN lattice, while the electronic effect has to be identical for both type of donors as discussed above.

Zoom In Zoom Out Reset image size

A remaining unknown figure in our experimental result is the offset of σ_a at $n\rightarrow 0$ where obviously σ_a must $\rightarrow 0$ as no doping-induced effects are present. The here found deviation can stem from uncertainties in the elastic constants C₁₁, C₁₂, and C₁₃ or wrong reference lattice parameters a₀ and c₀. More likely however, the presence of further defects can produce a deviation from Hooke's law in case of extended defects or a further unknown contribution to the size effect in case of further impurities not accounted for. The most likely dominating mechanism is a contribution by extended defects because all other parameters are found to be negligible. Nevertheless, the presence of extended defects, especially stacking faults in heteroepitaxial thin-film a-plane layers is no surprise [39, 40], and in our case approximately independent on the free carrier concentration as verified by studying the width of x-ray peaks. The effect of extended defects is consequently considered to be visible as an offset of $\Delta \sigma_a \approx -0.07\ \mathrm{GPa}$ in figure 2 independent on carrier concentration.

We use the elastic constants published in reference [41]. Applying equation (10) to all results presented in figure 1 simultaneously is equivalent to fitting β_tot in equation (9) so that the slope of the regression line in figure 2 is zero. We obtain for Si $\beta_{tot} = 0.7 \times 10^{-24}\ \mathrm{cm^{3}}$ and for Ge $\beta_{tot} = 1.9 \times 10^{-24}\ \mathrm{cm^{3}}$.

Comparing this result with our discussion above is encouraging. First, the β_tot value for Si is smaller than that for Ge in agreement with reference [4] and naive expectation from ionic radii. Second, the difference between both values $\Delta \beta = 1.2\times 10^{-24}\ \mathrm{cm^{3}}$ is nearly identical to the only available theoretical result of $\Delta \beta = 1.3\times 10^{-24}\ \mathrm{cm^{3}}$ [4]. Finally, both values of β_tot fit perfectly in the center of the expected range from the literature survey.

All samples were investigated by Raman spectroscopy from the sample surface in three different Raman configurations. In Porto notation [42], these are the $x(y,y)\bar{x}$ geometry, where the A₁(TO) and the E$_2^h$ modes are visible. Next is the $x(z,z)\bar{x}$ geometry with visible A₁(TO) phonon only, and finally the $x(y,z)\bar{x}$ geometry showing the E₁(TO) phonon. In this last configuration, with crossed polarizers, small residuals of the forbidden phonon modes A₁(TO) and E$_2^h$ can be visible due to sample imperfections or reflected Raman forward scattering.

The peaks in the Raman spectra were fitted by a sum of Lorentzian line shapes to account for lifetime broadened phonon modes:

$$\begin{equation} f(\omega) = \frac{A}{\pi}\frac{\gamma}{\gamma^2 + \left( \omega -\omega_0\right)^2}{^.} \end{equation} \tag{ 13 }$$

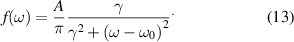
Here, A is the amplitude, γ the broadening, and ω₀ its characteristic energy. Figure 3 presents three representative Raman spectra and the corresponding fits in the frequency range of the E₁(TO) phonon mode for the $x(y,z)\bar{x}$ configuration. All three samples are Ge doped and a clear albeit small shift to lower frequency with increasing free electron concentration can be seen. It should be noted, that Si doped samples yield identical spectra as Ge doped samples for all phonon modes.

Zoom In Zoom Out Reset image size

The same fitting is performed for Raman spectra in all configurations (for the A₁(TO) phonon see figure 4) for all samples. Please note that the quality of all the fits is very good for the whole spectral range. For the further analysis, we use the phonon deformation potential set of reference [28].

Zoom In Zoom Out Reset image size

Because values for the phonon deformation potentials $c_{E_1}$ and $c_{E_2}$ are missing in this set, we study the A₁(TO) phonon first, where all phonon deformation potentials are known. Figure 6 presents the characteristic energy positions measured in $x(z,z)\bar{x}$ configuration², and deviations from the reference energy after applying corrections for the phonon deformation potentials and additionally the impurity-size effect, respectively. It is very obvious that the correction by phonon deformation potentials already explains most of the deviations of the experimental A₁(TO) phonon mode energy from the reference value. Taking into account the impurity-size effect as well does not visibly improve the agreement. This can be explained by the relatively high scatter of the data which in turn is understandable when taking the high full-width of half maximum of the A₁(TO) phonon and the presence of its anharmonic high energy shoulder [43], into account.

The same analysis for the E₁(TO) phonon mode as a function of free electron concentration is shown in figure 5 (top panel) for all samples. Plotted is the difference Δω from the reference value of the E₁(TO) phonon. The phonon energy shifts from about $560.5\ \mathrm{cm^{-1}}$ for low doping to $559.8\ \mathrm{cm^{-1}}$ at the highest Ge concentration.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

Correcting the experimental energy values by the phonon deformation potentials most of Δω vanishes (figure 5, mid panel). However at $n \gtrsim 4\ \times\ 10^{19}\ \mathrm{cm^{-3}}$ an increasing and systematic difference Δω is visible. We claim this remaining difference to be caused by the impurity-size effect. When correcting for the size effect (separately for Ge and Si), we end up with the results shown in figure 5 (bottom panel) where except few outliers all $\Delta \omega = \left( 0\ \pm\ 0.15 \right)\ \mathrm{cm^{-1}}$. To achieve this agreement, the values of β_tot for Ge and Si from above were used, but the phonon deformation potential $c_{E_1}$ was varied for minimum difference of the data points from the reference line. The result is $\left| c_{E_1} \right| = \left( 184\ \pm\ 80 \right)\ \mathrm{cm^{-1}}$. The same phonon deformation potential $c_{E_1}$ is used to plot the mid panel, too. A different value of $c_{E_1}$ would not change our results for β_tot but would require a different ω₀ instead.

As third phonon, we analyze the E$_2^h$ phonon which is only Raman active (figure 7). The phonon deformation potential $c_{E_2}$ is also not reported in reference [28]. However, as visible in equation (12), the E$_2^h$ phonon splits in two separate modes when $\left| \epsilon_a - \epsilon_m \right| \neq 0$ which is fulfilled in our a-plane samples. The slope of the energy difference between both modes then equals $2 c_{E_2}$. In Raman spectroscopy, we are able to observe both these modes in different configurations, namely in the $x(y,z)\bar{x}$ where it should be formally forbidden and the $x(y,y)\bar{x}$ configuration. Figure 8 displays the experimental results together with a linear fit (assuming no splitting for zero strain anisotropy) as a function of the strain. As result we obtain $\left| c_{E_2^h}\right| = \left(65\ \pm\ 20\right)\ \mathrm{cm^{-1}}$. Please note that the impurity-size effect does not alter this result significantly. Figure 8 is created by taking the impurity-size effect into account, but leaving it out, the result for $c_{E_2^h}$ is different by less then $0.2\ \mathrm{cm^{-1}}$.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The only other value for this parameter is given as $|c_{E_2^h}| = \left(379\ \pm\ 107\right)\ \mathrm{cm^{-1}}$ (table 1) which is on first sight not in good agreement. However, closer inspection of the source of this value [27], shows that the authors there consider it as an upper limit for $|c_{E_2^h}|$. Therefore, our result is in agreement with the result from reference [27].

The impurity-size effect is not obvious in figure 8 because nearly unaffected $\left| \epsilon_a - \epsilon_m \right|$ form the abscissa. The influence of the impurity-size effect is thus visualized in figure 9. The overall agreement of the shifted data points with the $\Delta \omega_{E_2^h} = 0$ line is slightly worse compared to the cases of the A₁(TO) or E₁(TO) phonons, especially at lower free-carrier concentrations. Because here, $\left| c_{E_2^h} \right|$ and the values for β_tot are obtained earlier with high accuracy and are simply entering the calculation, the remaining offset from the reference value might stem from (i) a slightly offset ω₀, (ii) propagation errors due to the used phonon deformation potentials or (iii) additional effects shifting the E$_2^h$ mode in our samples not covered by our model. Inspecting table 1 we find that the used phonon deformation potential set [28], for the E$_2^h$ mode is the only experimental one having $a_{E_2^h} < b_{E_2^h}$. Nevertheless, the agreement of model and experimental data is still very satisfying. A final judgment on the remaining small differences is not achievable in the framework of our study.

Zoom In Zoom Out Reset image size