Pricing games of NFV infrastructure providers

Abstract

Future online services will be provisioned over the federation of infrastructure providers for economic reasons: for effective usage of resources and for a wide geographic reach of customers. The technical enablers of this setup, envisioned also for 5G services, are the virtualization techniques applied in data centers, and in access and core networks. Business aspects around the provisioning of these services however pose still unresolved questions. In this heterogeneous setup those who want to deploy an online service face the problem of selecting the compute and network resource set that fulfills the technical requirements of the service deployment and that is preferable also from an economic point of view. Infrastructure providers compete among themselves for these customers, and shape their business offerings with profit maximization in mind. We model this resource market with the tool set of graph and game theory in order to study its characteristics. We show that customers need to tackle a hard problem if they want to meet both their technical and business needs, let alone minimizing costs. Furthermore, we derive the best pricing strategies that the providers should follow given their expectation about customers’ demand. Interestingly, we show that equilibrium prices and the attainable income strongly depend on the provider’s location within the network.

1 Introduction

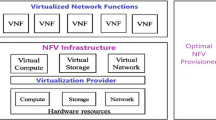
5G has been driving a revolution in the field of networking [1, 2]. The on-going and envisioned changes affect many other areas from cloud/edge computing to vertical industries including health care, Industry 4.0, and transportation [3]. In the visions of 5G the often heard service-level keywords are cost-effectiveness and improved service provisioning with fast creation, fast reconfiguration and with large geographical reach of customers. This paradigm shift is technologically enabled by Network Function Virtualization (NFV) [4], i.e., implementing telco functions in virtual machines that can be run on general purpose computers instead of running them on expensive dedicated hardware as the traditional manner, and by Software Defined Networking (SDN) [5], i.e., configuring and controlling network appliances with easily manageable, often centrally run software applications [6].

Due to this novel flexibility of the control and management of networking, new types of actors will enter the telco market, resulting in a largely heterogeneous ecosystem with currently unexplored business relationships among the stakeholders. For example, traditional telcos with physical resources and geographical footprint can provision basic Infrastructure as a Service (IaaS) (or NFVIaaS in the new context) for remote telcos without footprint, or for Over-the-Top (OTT) solution providers. But they can also extend their product range with Software as a Service (SaaS) offerings in order to step up in the value chain and to increase potential revenue. Alternatively, software solutions can be delivered by third party Virtual Network Function (VNF) developers, providing VNFaaS in this context even for the telco itself. We argue therefore that the new NFV ecosystem fundamentally redefines how telecommunications enterprises will soon operate not only from a technical, but also from a business perspective.

Online services can be best implemented as Service Function Chains (SFCs) [7] in which functions are run separately, possibly in remote data centers, while network control ensures connectivity between those and the end users. This tightly integrated environment encompassing cloud and network resources, together with the extreme service level requirements of verticals’ use cases, poses serious technological challenges on all stakeholders. The related issues seem hot topics and are being addressed by several research projects and working groups of standardization bodies initiated during the last few years [8, 9]. However, in our opinion the economic aspects and business related challenges have not received enough attention yet. This paper is a first step to establish a novel economic framework in order to understand the NFV ecosystem, to evaluate analytical models, and to propose novel pricing schemes and co-operation strategies among stakeholders.

In this paper we tackle the analysis of the expected business interaction between the infrastructure providers and the customers. More specifically, we are interested in how providers set their prices in such a market, and how customers select the necessary resources given those prices. To the best of our knowledge these questions have not been addressed before, even if there is a vast body of work related to the orchestration and management of NFV systems. We argue that price is an essential, if not the most important attribute of resources, therefore it is crucial to take it into account in resource orchestration methods. Our contribution is threefold: (i) we provide graph, probability and game theoretical models for the resources, customers’ demand characteristics and the providers’ pricing strategies respectively, (ii) we prove that resource allocation is a hard problem, (iii) we show the best resource pricing strategy for simple cases and building on the observations we deduce insightful consideration on pricing in general settings.

The paper is organized as follows. In Sect. 2 we introduce a model to describe the requirements of a service that a customer wants to deploy, and the attributes of the resources from which the customer selects. Building on the model, we define the provider-customer interaction as a game, and we formalize the resource selection problem. We show analytically proven optimal pricing strategies for stochastic games in which the customer behavior is modeled as random process, and resources are finite (Sect. 3) or infinite (Sect. 4). We evaluate realistic network topologies and show relevant results in Sect. 5 with the assumption of abundant provider capacities. Finally, we present related work in Sect. 6 and summarize our findings in Sect. 7.

2 Resource market model

Our work tackles the trades of resources that are necessary for deploying SFCs: computing power in data centers, and network bandwidth from the end-users, modeled as service access points, to data centers.

2.1 Actors and resources

We consider two types of actors in our model: the infrastructure (data center and network) providers and their customers, the latter possibly supplying application to the home user or to enterprises. We omit to include any other type of actors, such as the VNF providers mentioned in Sect. 1. The resources that are traded between these two types of actors are compute and network resources. Both types are offered with given capacity and tolling a given latency. Furthermore, we consider service access points as resources where the customers want to make their to-be-deployed service accessible to their customers. We build a graph model for these resources; an example illustration is shown in Fig. 1.

2.1.1 The graph model of providers

Let $\mathcal {A}$ denote the set of APs (service access points), $\mathcal {N}$ the set of NWs (network providers) and $\mathcal {D}$ the set of DCs (data centers).

Definition 1

We define resources as an undirected graph $G=(V,E)$ where V denotes the set of nodes and E the set of edges. There is a node assigned to each AP, each NW and each DC in G, thus the total number of nodes is $|V|= |\mathcal {A}| + |\mathcal {N}| + |\mathcal {D}|$. The following forms of edges can appear (see Fig. 1):

• AP–NW: each customer wants to create an online service that is reachable at one or more network providers;

• NW–NW: interconnect transit (Tier-1) and access (Tier-2 and Tier-3) networks that have direct links (representing peering) or connectivity at Internet Exchange Points, etc.;

• NW–DC: each DC is connected to the Internet via at least one network provider.

As illustrated in Fig. 1, the graph G has no edges between the nodes in $\mathcal {A}$ and no edges between the nodes of $\mathcal {D}$. Likewise, there are no edges connecting a node in $\mathcal {A}$ with a node in $\mathcal {D}$.

We denote the providers’ capacity with c, which can be either a network capacity $c_n$ for $n \in \mathcal {N}$, or compute capacity in a data center $c_d$ for $d \in \mathcal {D}$. We introduce $l_n$ for $n \in \mathcal {N}$ and $l_d$ for $d \in \mathcal {D}$ as the latency (i.e., delay) a network provider n and a data center provider d guarantees, respectively. For pricing, we use the notation p for the current price of resource units for both network and data center providers. Being part of the customer-facing network operators, the price is zero for AP nodes, i.e. $p_a=0$, $\forall a \in \mathcal {A}$, and those abstract nodes do not raise any technical obstacles, i.e., $c_a=\infty , l_a=0$, $\forall a \in \mathcal {A}$. The details are summarized in Table 1.

Fig. 1

Graph model of operators’ resources and service chains

Table 1 Summary of the applied parameters

2.1.2 The parametrized model of customers

Customers arrive with random demand for resources which are used for deploying a service for the customer’s end users. Demand characteristics include specific service access points, certain amount of computation and network capacity, maximum end-to-end latency and maximum total cost. Formally:

Definition 2

A given service request is defined by a 4-tuple $s = (a_s, c_s, l_s, b_s)$, describing

• 1. A selected access point $a_s \in \mathcal {A}$,

• 2. A required resource amount $c_s$ (capacity),

• 3. An upper limit $l_s$ on the end-to-end network latency that has to be met from AP to DC,

• 4. A budget $b_s$ that is an upper limit on the total cost the customer is willing to pay.

The request refers to a single time period as defined later. For the sake of simplicity, we assume in our model, that the amount of resources required by a request is characterized by a single parameter describing for instance either a measure of computation required to run the service in DCs, or corresponds to consumed network bandwidth at NWs. We do not consider multidimensional combinations of this parameter. This implies that any DC can serve any service, i.e., the computation never requires any special hardware. Notation is summarized in Table 1.

2.1.3 Provider-customer deals

Here we define the business interactions in the market, i.e., how deals are made.

Definition 3

Resource allocation A service request s is served through a path t or a set of paths $\mathcal {T}$ in G.

We first describe a service through a single path. A path t is a sequence of nodes $(a_{t}, n_{t, 1}, \ldots , n_{t, \ell (t)}, d_{t})$ where $a_{t} \in \mathcal {A},d_{t} \in \mathcal {D}$ and the number of its network providers is denoted by $\ell (t)$. The latency of the path is defined as the sum of the latencies of its network providers and the latency of its data center $l_{t} = \sum _{i = 1}^{\ell (t)} l_{n_{t, i}} + l_{d_t}$. The path is associated with the unit price $p_{t} = \sum _{i = 1}^{\ell (t)} p_{n_{t, i}} + p_{d_{t}}$ and an allocated capacity $c_{t}$. The allocated capacity must take into account the capacity of the resources along the path and the capacity allocated to other paths using them. To serve a request s the path t has to satisfy $a_{t} = a_s$, $c_{t} = c_s$, $l_{t} \le l_s$, $c_{t}p_{t} \le b_s$.

A request can also be served by a set of paths $\mathcal {T}$. In that case, we have for $t \in \mathcal {T}$:

• 1. Each path contains the requested access point $a_{t} = a_s$,

• 2. The total capacity of the paths equals the required capacity $\sum _{t \in \mathcal {T}} c_{t} = c_s$,

• 3. Each of the paths follows the latency constraint $\max _{t \in \mathcal {T}}(l_{t}) \le l_s$,

• 4. The total cost of the paths follows the price budget $\sum _{t \in \mathcal {T}}{c_{t}p_{t}} \le b_s$.

While serving service requests, each by its path or set of paths, it is required to follow the capacity constraints of all network components, i.e., to guarantee that for each component the sum of capacities allocated to paths containing the component is not larger than the capacity of the component.

2.2 Interactions on the resource market

We define the resource allocation and service provisioning time periods and their relation, illustrated in Fig. 2.

Definition 4

Resource allocation and service provisioning periods The resources that the customers lease are allocated for a fixed-length time period; this is the service provisioning period. Before this period, customers sequentially arrive with their service requests; that is what we call resource allocation period. Customers therefore book resources at the given cost at the selected providers during the resource allocation period for the service provisioning period.

Providers set price on their resources to be allocated for the service provisioning period. We assume that they maximize their expected profit for each service provisioning period. In order to do so they must take into account expected characteristics of demand (access points, capacity, latency, price budget) to appear during the resource allocation period. Furthermore, in any moment during the resource allocation period they have to consider the amount of resources that are already allocated for the given service provisioning period. They also have to compete with other providers’ prices, we suppose they have complete information in this aspect.

Customers behave as followers, acting on the prices the providers have set. Customers arrive in a sequence one after the other, and seek a set of resources that can serve their requests. In case there is no suitable set of resources to serve a customer request, i.e., no option that satisfies its access point, capacity, latency and budget parameters, the customer is not served. If customers react to prices offered by resource providers, it is the typical setup of a Stackelberg game: leaders, in this game the resource providers, choose their strategies, i.e., set their prices, by taking into account the expected selfish decisions that the customers, followers in this case, will make.

After a customer finds an eligible resource set and allocates it, the providers reset their prices based on the available capacities, becoming the leaders again for the time the next customer comes. This way the Stackelberg game repeats itself although not identically in various stages as available capacities are decreasing from one stage to the subsequent one, while the allocation of capacities are cumulating until the point when the resource allocation period ends and the service provisioning period starts.

Fig. 2

Resource allocation and service provisioning periods: in each time period (of a fixed length R) the served requests are those that arrived in the previous period

In the following we show how the followers can determine their best response strategies.

2.3 Customer strategy: the path/flow selection problem

Any given customer with a service request $s = (a_s, c_s, l_s, b_s)$ during the resource allocation period would like to find a path (or a set of paths) with a total cost under its budget, while preserving the technical demands of s (on its access points, capacity and latency). The requested access point constrains the selection to be among a smaller resource subset. Similarly, the capacity requirement implies a subset of the network components from which the path can be found, following their available capacities. The impact of the latency and the budget constraints has a different flavor since these two metrics of a possible path (or a set of paths) are calculated in an aggregated way along the path resources. Accordingly, the path should be found while considering the following problem: given a network subset, find a path (or a set of paths) that preserves both the latency and budget constraints.

Theorem 1

The problem of finding an eligible flow with at most $b_s$ budget (or the cheapest eligible flow) is NP-hard if the network is an arbitrary graph.

Proof

(Proof Outline) The problem of finding an eligible flow with at most $b_s$ budget is the associated decision problem of finding the cheapest eligible flow problem. The latter problem is, on the other hand, equivalent to the shortest weight-constrained path problem, known to be NP-complete ([10], page 214). In this problem, given a graph in which each edge is associated with a length and a weight, it is required to determine whether there exists a path satisfying two upper bounds on its total length and weight. Even though in this problem values refer to links while in ours to nodes (latency and price), we can deduce the hardness for our problem. Note that polynomial-time algorithms exist for cases where all link weights are equal or alternatively all links have the same length. $\square$

Due to the NP-hard nature of the eligible flow finding problem, we assume that the sequentially arriving customers apply heuristics when selecting the resource set to allocate. For this reason and because the service request parameters cannot be known in advance, in the next section we model the pricing game as a stochastic game, the customers being the randomness with a probabilistic behavior of setting request parameters and selecting paths.

3 Equilibrium prices in pricing games

In this section we list the analytical results of the evaluation of the pricing game. We set the stage for the stochastic game between the providers, given that customer requests are random in terms of parameters and selected paths. Then we examine three simple topologies and describe the equilibrium prices in those games.

3.1 Stochastic game model

As customers face an NP-hard problem with the eligible flow selection, we reduce the Stackelberg game, where providers are leaders, customers are followers, to a stochastic game among providers as players. In this stochastic game, the state is the available capacity level of resources at providers, the actions (or strategies) of the players are the prices that the providers set for themselves, and the transition probability function is determined by the probabilistic type of the customer that arrives next, and the path(s) it selects. Depending on which providers are chosen at resource allocation, which is a heuristic decision, providers’ payoffs increase by a reward based on their given prices. In the rest of the paper we assume that customers allocate single paths (instead of flows), and thus we define the random variables of service requests as follows.

Definition 5

Let $\mathcal {S}$ denote the set of all possible requests and S the random variable of the next request. We define the random variable of service request by the tuple $S = (A,C,L,B)$, where we denote the random variables of the requested access point, the requested capacity, the latency constraint and the price budget by A, C, L and B, respectively. We suppose that each service s selects a single path during resource allocation from its access point $a_s$. Let $\mathcal {T}_s$ be the set of paths from $a_s$ to $\mathcal {D}$ such that all of its elements satisfies $C_s$ and $L_s$. Given $\mathcal {T}_s$, the tuple $(T_s,B_s)$ fully defines the service request, where $T_s$ is a random variable on $\mathcal {T}_s$. The path is chosen independently from the prices; if the selected path is costlier than the budget constraint, the request fails.

Feasible requests select such paths that satisfy capacity, latency and budget constraints. In such a setup, the central question is: what is the winning policy of the game players, i.e., the resource providers? In order to answer that, we seek the value of the game [11] for each player that gives the best-response actions in Markov-perfect equilibrium. Before doing so, we make an assumption on the memoryless arrival process.

Assumption 1

The number of requests during the resource allocation period follows geometric distribution with parameter q. Namely, each request is the last one with probability q and at least one other request follows with probability $1-q$.

Without the loss of generality, we can suppose there is one element in $\mathcal {D}$, i.e., there is only one data center node in the topology under investigation, and its unit price is 0. If this is not true, i.e., if there are more elements in $\mathcal {D}$ or the one element’s unit price is not 0, then for the analysis we turn the elements in $\mathcal {D}$ into elements in $\mathcal {N}$ with the same properties and insert an additional element into $\mathcal {D}$, connected to all original data center nodes. Assuming infinite capacity, zero delay and zero price for this one data center, we arrived to our initial assumption, keeping the original topology’s characteristics intact from the analysis point of view.

Fig. 3

Topologies with a single AP, a 1 or 2 DCs and 0 or several NWs

For illustrative purposes, in the following sections we derive the equilibrium strategies for selected settings: the network topologies of providers represent both serial and parallel setups, latency constraints are supposed to be met for all eligible service requests, demanded capacity is fixed to one unit (large capacity services might be modeled by a number of unit-sized requests), and the price budget parameters of service requests are randomly drawn from uniform distributions. The goal of the analysis is to formulate the best response strategies, i.e., the prices that providers set as their actions, through first determining the value of each game. We present 3 cases, as depicted in Fig. 3. With these illustrative examples we present how the expected number of subsequent requests and the graph topology of interconnections determine the pricing strategies of the providers.

3.2 The effect of decreasing capacity

The example of Fig. 3a shows how sequential allocations affect price, i.e., how to maximize revenue by setting a price with the expectation of future service requests. We suppose a widely used arrival process of Assumption 1: the probability of receiving a next service request does not diminish over time. Let $V^1$ denote the value of this game, although there is only one player here, hence the superscript, which is technically a decision problem. The recursive solution by capacity gives the following result for the provider with capacity c and price p.

Lemma 1

If Assumption 1 holds, the value of the game is

$$\begin{aligned} V^1(c,p)= \frac{\mathbb {P}(Z)\big (p\mathbb {E}(C|Z)+(1-q)\mathbb {E}(W^1(c-C)|Z)\big )}{q+\mathbb {P}(Z)(1-q)}, \end{aligned}$$

where $W^1(c)$ is the optimal value of the game for one player with c capacity, $\mathbb {P}(X)$ stands for probability of a stochastic event X, $\mathbb {E}(Y)$ denotes the expected value of a random variable Y, and $Z {\mathop {=}\limits ^{{ \text{ def }}}}(B \ge pC)$, i.e., the event of $B \ge pC$.

Proof

In general, the value of the game is

$$\begin{aligned}&V^1(c,p)=\mathbb {P}(Z)(p\mathbb {E}(C|Z)+(1-q)\mathbb {E}(W^1(c-C)|Z))\nonumber \\&\quad +\,(1-\mathbb {P}(Z))(1-q)V^1(c,p). \end{aligned}$$

(1)

Z means that the request has enough budget to pay the price. When Z holds, the price p is paid, a capacity of $c-C$ remains for future requests. When Z does not hold, a value might be gained only from subsequent requests. $\square$

Building on Lemma 1, and supposing unit-sized capacity requests and uniform distribution of budgets, we derive the closed-form formula of the equilibrium price.

Assumption 2

Service requests’ capacity values are fixed $C\equiv 1$, budget constraint follows uniform distribution (denoted by $U(\min ,\max )$), without loss of generality $B \sim U(0,1)$.

Proposition 1

If Assumptions 1 and 2 hold, then the optimal price in the setup of Fig. 3a is:

$$\begin{aligned} p^* = \frac{1- \sqrt{1-(1-q)\left( 1-(1-q)qW^1(c-1)\right) } }{1-q}. \end{aligned}$$

Proof

From Lemma 1 the value of the game for $c >0$ is

$$\begin{aligned} V^1(c,p)= \frac{(1-p)\left( p+(1-q)W^1(c-1)\right) }{q+(1-p)(1-q)}, \end{aligned}$$

and $V^1(0,p)=0$. In order to maximize the above function we get its derivative, which leads to the following equation for $p^*\in (0,1)$: ${p^*}^2(1-q)-2p^* +1-(1-q)q W^1(c-1) =0$. From there, the statement is straightforward after some algebra. $\square$

As for the equilibrium strategy, we know that $p*=\arg \max _pV^1(\hat{c},p)$, so denoting $\max _pV^1(\hat{c},p) = V^1(\hat{c},p^*)$ as $V^1(\hat{c})$, we have $V^1(0)=0$ and $V^1(1)=\frac{1}{(1+\sqrt{q})^2}$ with $p*=\frac{1}{1+\sqrt{q}}$. For further values of $\hat{c}>1$, we solve the recursive formula $p^2(1-q)-2p + (q-1)q V^1(\hat{c}-1) + 1=0$, $p\in (0,1)$ for ${p^*}$ numerically. In Fig. 4 we plot the equilibrium prices for different provider node capacities, i.e., $c \in [1,30]$, and geometric distribution parameters, i.e., $q = \{0.1, 0.2\}$. First, we can see that higher chances for the arrival of subsequent requests (low values of q) motivates the resource provider to demand a higher price. On the other hand, having a larger capacity for the resource, motivates it not to be strict and to accept requests with lower budgets. Inspired by the observations of the numerical solutions depicted in Fig. 4, we derive the equilibrium price of the game analytically for $c=\infty$: when serving a request has no negative impact on the remaining capacity, the resource provider tries to maximize the value obtained from every request independently. We prove that the price should not be too low or high in terms of the budget distribution.

Proposition 2

If Assumption 2 holds and the provider’s capacity is infinite, i.e., $c=\infty$, the equilibrium price is $\frac{1}{2}$.

Proof

With $c=\infty$ the game reduces to focusing on a single request. Then similarly to Lemma 1 the value of one stage is: $V^1(\infty ,p)=p \mathbb {P}(B\ge p) = p(1-p)\rightarrow p^* = \frac{1}{2}.$ $\square$

Namely, with infinite capacity, providers maximize the profit from each request, independently. While setting a high price can increase the profit when taken, it has lower chances to be a part of a selected path. With a uniform distribution of the budget $B \sim U(0,1)$, we get that the equilibrium price is 0.5.

Fig. 4

Equilibrium prices for various c, q values in the single NW topology

3.3 Pricing against fellow providers

Here we analyze the game in which k network providers are adjacent to each other, as depicted at Fig. 3b. Similarly to the previous case, we can determine the equilibrium prices for the restricted case of uniformly distributed price budgets and fix capacities in the service requests.

Proposition 3

If Assumptions 1 and 2 hold, and the number of network providers is k in the serial setup, then for the Nash-equilibrium we have the following equation: $0=k^2(1-q){p^*}^2-p^*(2k-q(k-1))+1-q(1-q)W^s(c-1).$

Proof

Similarly to Lemma 1 the value of the game is:

$$\begin{aligned} V^s_i(c,\mathbf {p})= \frac{(1-\sum p_j)(p_i+(1-q)W^s_i(c-1))}{q+(1-\sum p_j)(1-q)}, \end{aligned}$$

where $V^s_i$ is the game value for provider i (s superscript as in serial), and $\mathbf {p} = (p_1, p_2, \dots , p_k)$. The numerical analysis of the equilibrium prices is based on the observation that the network provider nodes have symmetrical role, so we suppose $p^*_i=p^*~\forall {i}$. Then we have the above equation for $p^*$. $\square$

Fig. 5

Equilibrium price $p^{*}(c)$ for $k \in [1,10]$ providers and arrival q=0.1. Markers are used to describe the price for a finite capacity $c \in [1,20]$ and a solid line for an infinite capacity $c=\infty$

In Fig. 5 we plot the numerical values of prices calculated with the formula in Prop. 3, now in the function of the number of providers ($k=[1,10]$), and their capacities ($c=[1,20]$). The expected number of requests is 10, i.e., $q=0.1$. Results show that prices are inversely proportional to the number of players, and converge fast as the values of capacities leave the range of under-provisioning. Again, inspired by these results, from Prop. 3 we have the following direct consequence for the case where network capacities are unlimited. For this latter case, a solid blue line depicts the numerical values in Fig. 5.

Proposition 4

If Assumption 2 holds and the providers’ capacity is infinite, i.e., $c_i=\infty$, then the equilibrium price and ratio to the the price of anarchy for k nodes are:

$$\begin{aligned} p^* = \frac{1}{k+1}, ~ PoA = \frac{(k+1)^2}{4 k} \end{aligned}$$

Proof

To derive equilibrium prices for infinite capacities it is enough to focus on only one request. The value of a request is $p_i(1-\sum p_j)$. It is maximal if $2p_i = 1-\sum _{j\ne i}p_j$, and in equilibrium $p_i^*$ are the same, so $p^*=\frac{1}{k+1}$. For k providers the price of the path is $\frac{k}{k+1}$, so the value for one provider is $p^*\mathbb {P}(B>\frac{k}{k+1})=\frac{1}{k+1}\frac{1}{k+1}$. The game value for one request is $W^s(\mathbf {\infty })=\frac{1}{(k+1)^2}$, and for the whole game it is $V^s(\mathbf {\infty }) = \frac{1}{1-q}W^s(\mathbf {\infty })$. If providers maximized the sum of their game values, the sum of probability would be $\frac{1}{2}$, which would lead to $p=\frac{1}{2k}$ and for the maximal value it would give $\frac{1}{4k}$. $\square$

The inter-dependent providers drive their prices to an inversely proportional drop, and to a slight increase in the total price for the customer. The price of anarchy grows linearly with the number of providers: the longer the chain of providers, the further they shift away from Pareto optimum.

3.4 The effect of competition

After the examples of one, or more players on the same path, optimizing their expected total income over the resource allocation period, now we turn to the simplest competitive game of “substitute” providers. In this setting two DC providers are both connected to the AP in parallel, posing direct competition to each other. This is the scenario depicted in Fig. 3c. Let $V^p$ denote the value of this so-called parallel game.

Now we give the general formula for the value of this game, assuming that the arrival process of service requests is memoryless. If Assumption 1 holds, then:

$$\begin{aligned}&V^p_1(\mathbf {c,p})\\&\quad =\frac{\mathbb {P}(S_1\wedge S_2)}{2}p_1\mathbb {E}(C|S_1\wedge S_2)\\&\qquad +\,\mathbb {P}(S_1\wedge \overline{S_2})p_1\mathbb {E}(C|S_1\wedge \overline{S_2})\\&\quad \qquad +\,(1-q)\left[ \mathbb {P}\right. (S_1\wedge S_2)\frac{1}{2}\mathbb {E}(V^p_1(c_1-C,\hat{c}_2)\\&\quad +\,V^p_1(c_1,c_2-C)|S_1\wedge S_2)\\&\qquad +\,\mathbb {P}(S_1\wedge \overline{S_2})\mathbb {E}(V^p_1(c_1-C,c_2)|S_1\wedge \overline{S_2})\\&\qquad +\,\mathbb {P}(\overline{S_1}\wedge S_2)\mathbb {E}(V^p_1(c_1,c_2-C)|\overline{S_1}\wedge S_2)\\&\qquad \left. +\,\mathbb {P}(\overline{S_1}\wedge \overline{S_2})V^p_1(\mathbf {c,p}) \right] , \end{aligned}$$

where $S_i {\mathop {=}\limits ^{{ \text{ def }}}}(C\le c_i)\wedge (p_i\le B)$, $\mathbf {c}=(c_1,c_2)$, $\mathbf {p}=(p_1,p_2)$, and $\bar{S}$ denotes the complement of S.

In case of uniform budgets and unit-sized jobs, the price strategies are delivered by the following formula.

Proposition 5

If Assumptions 1 and 2 hold, in the two-player parallel game the solution of these equations provide the equilibrium prices for the 2 players, denoted by i and $-i$:

$$\begin{aligned} 0&={p^*_i}^2(1-q)-p^*_i(4-2p^*_{-i}(1-q))+2\\&\quad -\,(1-q)(2W^p(c_i-1,c_{-i})+p_{-i})\\&\quad +\,(1-q)^2(p_{-i}(W^p(c_i-1,c_{-i})-W^p(c_i,c_{-i}-1))\\&\quad +\,(1-q)^2(W^p(c_i-1,c_{-i})+W^p(c_i,c_{-i}-1)). \end{aligned}$$

Proof

Similarly to the previous cases, the value of the game for the first provider can be written as:

$$\begin{aligned}&V_1^p(\mathbf {c},\mathbf {p})=\frac{(1-q)(1-p_1)W^p(c_1-1,c_2)}{2-(1-q)(p_1+p_2)} \\&\quad +\,\frac{(1-q)(1-p_2)W^p(c_1,c_2-1)+p_1(1-p_1)}{2-(1-q)(p_1+p_2)} \end{aligned}$$

By deriving it according to $p_1$, we get the equation above. $\square$

If provider capacities are infinite then the game is again reducible to the case of only one request. In that case the providers’ game values are independent from each other, which means the game reduces to the single node case, where the optimal price is $\frac{1}{2}$. The numerical solution of Prop. 5 depicted in Fig. 6 shows in the case of $q=0.1$ how the equilibrium price converges to $\frac{1}{2}$ as the capacities go to infinite. It also means that the price of anarchy converges to 1 for this topology, as in the single node case. The prices in case of infinite provider capacities are depicted again by solid blue lines in Fig. 6.

Fig. 6

Equilibrium price $p_1^{*}(c_1,c_2)$ for provider capacities $c_1,c_2 \in [0,20]$ and arrival $q=0.1$. Markers are used to describe the price for finite capacities $c_i \in [0,20]$ and a solid line for infinite capacities $c_i=\infty$

Based on the numerical results, for this case of parallel providers, we make the following conjecture.

Conjecture 1

If capacities are infinite in nodes and $B\sim U(0,1)$ then the equilibrium price and the game value for n parallel players for one request are:

$$\begin{aligned} p_i^*&=\frac{\left( {\begin{array}{c}2n\\ n\end{array}}\right) }{2\,4^{n-i}\left( {\begin{array}{c}2i\\ i\end{array}}\right) }\sim \frac{\sqrt{i}}{2\sqrt{n}},~ W_i^p(\mathbf {\infty })\\&=\frac{1}{i}{p_i^*}^2\sim \frac{1}{4n}. \end{aligned}$$

In the next section we investigate such cases in which the providers’ capacity can be treated as infinite, compared to that of a single request.

4 Analysis of infinite-capacity games

Hindered by the complexity of the game analysis, and building on the observation of fast price convergence in function of provider capacities, in this section we relax the capacity constraints of service requests. By doing so, first we derive the equilibrium prices for an artificial, but more complex topology than the previous ones; second, we formulate equations that provide equilibrium price values for general topologies.

Assumption 3

Network and compute providers have sufficient capacity to accommodate service requests: the set of available paths of a given request is not limited by capacity constraints.

4.1 Equilibrium prices for topologies with multiple APs

Here we show the equilibrium prices for the topology shown in Fig. 7: in this artificial topology we draw k chains of NWs with different lengths that connect k APs to the same DC. The equilibrium prices are given in the next proposition.

Fig. 7

Parallel paths with serial NWs

Proposition 6

If Assumptions 2 and 3 hold, the topology is as it is given in Fig. 7 and the requests contain uniformly the k APs, then the equilibrium prices are:

$$\begin{aligned} p^*_D=\frac{H_k}{k+H_k},\, p^*_i=\frac{k/i}{k+H_k},\, PoA\sim \frac{k+H_k}{4 H_k} \end{aligned}$$

where $p^*_D$ is the price of the DC, $p^*_i$ is the price of nodes in chain with $i-1$ NWs and $H_k=\sum 1/j\sim \ln k$.

Proof

Assuming that the providers in the same chain have the same optimal price, from the derivatives of the value functions we have the following equation for $p_i~i\in [2,\dots , k]$ and $p_D$:

$$\begin{aligned} p_i = \frac{1-p_D}{i},\quad p_D=\frac{k-\sum (i-1)p_i}{2k}. \end{aligned}$$

$\square$

On one hand, $p_D\sim \frac{\sum 1/i}{k}$, i.e., the data center’s price is proportional to the average of the path length reciprocals. On the other hand, the even more important result from this topology is that if k is large enough, then $p_i^*\sim 1/(i+1)$, where i is the length of the path that contains the node. With this observation in hand, we now turn to another topology in which network provider nodes are situated on shared paths to the same DC.

Fig. 8

The pine-tree topology

In this second case the topology, depicted in Fig. 8, contains a chain of k providers and each of them has an AP, and there is one DC at the end of the chain.

Proposition 7

If the topology is the same as in Fig. 8, and the requests arrive uniformly from the k APs, then the Nash-equilibrium is:

$$\begin{aligned} p_i^*=\frac{e_i(i+1)(i+2)\dots k}{(e_i+i)(e_{i+1}+i+1)\dots (e_k+k)}, \end{aligned}$$

where $e_1=1$ and $e_{i+1}=\frac{i+(i+1)e_i}{i+e_i}$. NW nodes are enumerated based on the number assigned to their connected AP as depicted in Fig. 8.

Proof

As $V_i(\mathbf {p})=\frac{1}{k}p_i\sum _{l=1}^i\left( 1-\sum _l^kp_j\right)$, considering the equations $\frac{\partial }{\partial p_i} V_i=0$, we get the following equations: $p_i=\frac{e_i}{i+e_i}\left( 1-\sum _{i+1}^kp_j\right)$, which gives the above solution. $\square$

Figure 9 shows that in the numerical evaluation of the above formula the price monotonously decreases NW node-by-NW node going from the DC towards the edge, i.e., providing transport for fewer and fewer APs. Calculations were run for different values of k: [2, 10], lines represent the simulations, the more nodes are involved, lower the price curve is located on the plot.

Fig. 9

Equilibrium price for NW nodes according to their distance from the DC in the top (x axis: i, y axis: $p_i^*$), and the same distance-dependent prices, but the sequential number of nodes are normalized by $k+1$ in the bottom (x axis: $i/(k+1)$, y axis: $p_i^*$) figure. One line corresponds to one numerical evaluation of formula in Prop. 7 for a given k value

4.2 Equilibrium prices in general topologies

In the following we formulate the equations that give equilibrium prices of the providers for general topologies. If t is a requested path then let us denote with $\overline{t}$ the set of vertices on t except the service access point.

Proposition 8

If Assumptions 2 and 3 hold we have the following equations for the prices for all $x\in G\setminus \mathcal {A}$:

$$\begin{aligned}&0=\sum _{s\in \mathcal {S}}\sum _{x\in t, t\in \mathcal {T}_s}\mathbb {P}(S=s,T_s=t) \\&\qquad \left[ \left( 1-F_{B_s}\left( \sum _{y\in \overline{t}}p_y\right) \right) -f_{B_s}\left( \sum _{y\in \overline{t}}p_y\right) p_x\right] \end{aligned}$$

Proof

For every $x\in G\setminus \mathcal {A}$, $V_x$ denotes the value of the game and $p_x$ the unit price of resource provider x respectively.

$$\begin{aligned} V_x= \sum _{s\in \mathcal {S},t\in \mathcal {T}_s,x\in t}\!\!\!\mathbb {P}(S=s,T_s=t)\left( 1-F_{B_s}\left( \sum _{y\in \overline{t}}p_y\right) \right) p_x \end{aligned}$$

If $\frac{\partial }{\partial p_x} V_x=0$, then we get the above equations. $\square$

In the next section we evaluate the connection between equilibrium prices and topology attributes of the providers based on this last proposition. Before jumping to numerical analysis, we make an important statement for cases in which customers’ path selection is not random, instead determined by Assumption 4 below. We implement the following path selection policy for customers also in the numerical simulations that we present in the next section.

Since finding the cheapest eligible path is NP-hard (see Theorem 1) we suppose that customers do not solve this problem. Instead we propose for the customers to use the following heuristics to select a path in polynomial time: choose the eligible path with minimum number of hops. It is well known that the shortest weight-constrained path problem is polynomial if the link weights are equal, and in this case they are all ones. The reason to apply this heuristics is that as we see in Prop. 6 the shorter a path (in hops), the cheaper. We believe this is true in general situations, not only in the case of Prop. 6.

Assumption 4

Let all $a\in \mathcal {A}$ deterministically choose the shortest path (in terms of hops) which is eligible, $t_a$, to the closest $d \in \mathcal {D}$. In this case $\mathcal { S}=\{s_a|a\in \mathcal {A}, s_a=(t_a,B_a)\}$.

Assuming this shortest path selection policy, Prop. 8 directly leads to the next consequences.

Corollary 1

If Assumptions 2, 3 and 4 hold we have the following linear equation system on the probability of a provider being on a path selected by a service request. The equilibrium prices can be calculated from these equations.

$$\begin{aligned}\mathbb {P}(x\in \overline{T_S})=\sum _{a\text { if }x\in \overline{t_a}}\mathbb {P}(S=s_a)\left( p_x +\sum _{y\in \overline{t_a}}p_y\right) ,\end{aligned}$$

$\forall x\in G\setminus \mathcal {A}.$

Corollary 2

If Assumptions 2, 3 and 4 hold all used AP–DC paths have the same length, and the number of non-AP nodes on the path are k ($\forall a\in \mathcal {A}, |\overline{t_a}|=k$), then the equilibrium prices are $p_x=\frac{1}{k+1}$ for all $x\in G\setminus \mathcal {A}$.

Moreover, we can also deduce the price of anarchy.

Corollary 3

For the case Assumptions 2, 3 and 4 hold, the price of anarchy can be calculated from the equilibrium prices $p_x$ for $x\in G\setminus \mathcal {A}$ by the following way:

$$\begin{aligned}~ PoA = \frac{1}{4\sum _{a\in \mathcal {A}}\mathbb {P}(S=s_a)(1-\sum _{y\in \overline{t_a}}p_y)(\sum _{y\in \overline{t_a}}p_y)}.\end{aligned}$$

Proof

The sum of the game values can be maximized by the following way: DCs set the price to $\frac{1}{2}$, NWs set the price to 0. In this case the maximum is $\frac{1}{4}$. $\square$

Corollary 1 provides an equation system that gives the equilibrium prices of any given topology; we use those in our simulations in the next section. Corollary  2’s statement is similar to those that we made for special cases in the previous section, but in this case it stands for general topologies. The importance of this statement is supported by the fact that in realistic settings APs are typically at the edge of the network, while DCs are in the center, so the length of most of the paths equals to the radius of the network. Finally, Cor. 3 provides the formula for the price of anarchy. In cases when paths typically contain 4 providers, $PoA\sim 1.5$, if they contain 10 providers the $PoA\sim 3$. In the simulations presented in the next section, the PoA is around 1.3, as there are really few paths containing many providers.

5 Numerical evaluation of realistic topologies

In this section we highlight interesting relations between a provider’s price and its situation in the topology, and we show with simulation results that our analytically derived equilibrium prices ensure high income even without assuming infinite provider capacities.

We simulated various topologies to examine how topological parameters affect the price a network or a data center provider sets. The generated topologies include both arbitrary and hierarchical ones. The hierarchical topologies are generated in order to best reflect real topologies of network interconnections: we set the simulation parameters based on real situations dealing with telecom and network operators, and with data center services providers. Hierarchical topologies have three tiers of NWs: in the highest tier we assume Tier-1 operators, e.g., CenturyLink (former Level 3), Telia, AT&T [12], while in the lower tiers we assume Tier-2 and Tier-3 telecom operators and internet service providers with national and multinational coverage, e.g., Comcast, Vodafone, China Telecom, etc. An illustration of the tiered relations of network providers is depicted in Fig. 10 where Points of Presence (PoPs) correspond to APs and DCs in our model, and an Internet Exchange Point (IXP) gives the possibility of peering between Tier-2 providers.

Fig. 10

Relationship between the various tiers of Internet providers, source: Ludovic.ferre-Internet Connectivity Distribution&Core.svg, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=10030716

In the highest tier Transit NWs form a mesh and interconnect the Edge NWs of the lower tiers. Edge NWs provide connectivity to APs and DCs and may also have peering links with other Edge NWs (Tier-2 networks). In terms of data center providers, i.e., DCs, we can find a lot of different market players, from the top public cloud providers, e.g., AWS, Google, Microsoft Azure, across the biggest colocation data center providers, e.g., Equinix, Zayo [13], to many smaller ones. Rickard et al. [14] contains high level figures on carrier-based cloud interconnects and cloud endpoints offered by the largest network providers. We set the simulated number of DCs per NW in our experiments accordingly.

In Sect. 3 we showed that the equilibrium prices converge fast in the number of providers and their capacity, thus for acceptable simulation runtimes we scaled down the number of simulated NWs and DCs from the global scale of thousands of network providers and hundreds of data center operators: we generated topologies randomly with different number of NWs ranging from 15 to 50, and of APs and DCs ranging from 2 to 15. We assumed that all NWs and DCs had capacity $c=20$ and we randomly assigned delay parameter values to them from U(1, 100), mimicking network delays in the order of milliseconds.

In contrast to the infrastructure, data is not available publicly in terms of the amount of data center hosted applications and the number of tenants. However estimations on the size of the global colocation data center market are available by several surveys [15, 16], and the estimations vary around 50 billion USD, while the total size of the public cloud computing market is estimated to be between 250 and 350 billion USD [17,18,19] in 2020. While the former consists of multi-tenant data centers including wholesale, colocation, managed and shared hosting data centers, the latter further includes hyperscale data centers offering cloud services at Infrastructure as a Service (IaaS), Platform as a Service (PaaS), and Software as a Service (SaaS) levels. The general trend shows large hyperscale data centers being deployed at select locations that fulfill several criteria, e.g., cheap power, cooling, excellent network connectivity, and a slowing growth of enterprise and colocation data centers.

Due to the lack of input data on the amount of cloud-deployed applications, the number of requests generated for each AP in each setup is determined by a geometric distribution with the following values $q=\{0.0025, 0.005, 0.01, 0.02, 0.05\}$. The generated requests are randomly assigned to different APs in a uniformly distributed way. Each request (i) demands $C\equiv 1$ unit of capacity from each NW and DC that will participate in the service chain, (ii) has a budget $B \sim U(0,1)$ that the customer is willing to pay and (iii) has a maximum end-to-end latency requirement $L \sim U(1,100)$ that should be satisfied.

5.1 How topological attributes drive prices?

In the first set of results, we focus on the average length of the shortest paths in which a provider participates. This is related to the average distance of a data center provider from $\mathcal {A}$ and that of a network provider from $\mathcal {A}$ and from $\mathcal {D}$. For each AP we find an eligible path to a DC as Assumption 4 suggests, i.e., the shortest (in hops) eligible path to a DC, and we assign prices to the nodes of this path according to Cor. 1.

The simulation results reveal that the average length (in hops) of paths a NW provider n belongs to is of high importance both for arbitrary and hierarchical topologies. In particular, the lower the number of hops between n and $\mathcal {D}$ is, the higher n’s equilibrium price is. On the other hand, the average distance of n from $\mathcal {A}$ does not show any correlation with n’s price.

In Fig. 11 we plot the equilibrium price in function of the reciprocal for the harmonic mean of the length of paths that a provider lies on. If a provider participates in shortest paths with a low length average, then its price is high. As we see in Prop. 6 the equilibrium prices are close to the average of the reciprocals for their path lengths. In Fig. 11 we can see that DCs choose their prices close to our theoretical estimation and NWs’ prices are also close to the linear line given by the analysis. Providers who typically take part in twice longer paths, choose half the price.

Fig. 11

Equilibrium prices of data center and network providers in function of the average length reciprocals of shortest paths that include them

5.2 Can the provider raise profit with other pricing?

We numerically show here that even though the equilibrium pricing policy we calculated assumes infinite provider capacities, for most of the cases in terms of topology, capacity, latency and budget inputs, those prices are indeed the best response. For the evaluation we assume that one provider node does not follow the proposed pricing policy, instead either sets its price above or under the equilibrium price. The network provider n that deviates from the “equilibrium” pricing policy is randomly selected, and it alters its price by $\pm 0.1$: $p_n' = p_n^*\pm 0.1$.

Figure 12 shows that n’s profit is lower than the average profit of the other providers. Results are averaged for over 100 runs. This proves that although finite provider capacities are simulated, the equilibrium prices ensure higher payoff to the players than any other strategies.

Fig. 12

The impact of number of service requests on the profit of the deviating provider ($c=20$, 10 APs, 20 NWs and 10 DCs)

6 Related work

The body of research on pricing IT resources in general is vast. We study the pricing of NFVI resources in our work. While major effort lies within the design and evaluation of NFV management and orchestration solutions [20], interestingly there are no proposals for pricing or including prices in orchestration methods among ETSI NFVO standards [21], and to the best of our knowledge only a few research works have addressed only partly these problems so far. We review related works separated based on whether they address the pricing of resources in a single, or a multi-administrative domain setup.

6.1 Pricing in clouds and network slicing

Managing network and cloud resources together in cloud networking has many challenges. A recent survey [22] reviews pricing models for resource management in this scope. Most of the collected works propose the application of dynamic pricing, as it increases seller’s profit when two product characteristics co-exist: first, the product expires at a point in time, second, capacity is fixed and it is costly to be augmented. Both are true for the market of leasing data center resources.

When goods are sold with dynamic pricing, either markets generate the prices, e.g., in auctions, or sellers apply pricing schemes and market mechanisms to adapt dynamically to the demand. A real-world example for the former is a spot market where the price is given by the intersection point of demand and supply, as for Amazon EC2 Spot Instances [23]. In the latter case, there are various techniques for maximizing seller surplus. In [24] the authors strategies that a provider can use to improve revenue, including resource throttling. Bega et al. [25] presents an algorithm for the admission and allocation of network slice requests that maximizes the infrastructure providers revenue. The authors of [26] apply the share-constrained proportional allocation mechanism for network slicing.

6.2 Pricing of NFVI for multi-administrative domains

The term cloud networking is understood in a multi-administrative domain scenario in which network and data center domains interact with each other. Nevertheless, the exhaustive collection of related work presented in [22] does not include research results that tackle both multiple providers and various resource types to sell. The possible reason for the lack of pricing aspects within NFV MANO frameworks is that they mainly target a single administrative domain. In the multi-provider NFVI market however, for the implementation of the visions of 5G it is necessary to price cloud and network resources in a market for many providers and customers.

The following related works made modeling and evaluation steps in this direction. In [27] the authors analyze pricing schemes for the joint provisioning of radio access capacity and mobile edge computing services in a multi-tenant Radio Access Network. A usage-based dynamic pricing scheme applied for NFCs is presented in [28]: the authors derive the prices, based on the actual utilization and on historic data, that maximize the potential income of the provider.

7 Conclusion

In the epicenter of the envisioned 5G ecosystem compute and network resources are allocated via an NFVI market across multi-administrative domains. Customers include Over-the-Top application providers who offer services to home users, enterprise application providers who provision business services, etc. On the other side of the market, providers are compute infrastructure and network operators, given the ability of online service deployments, i.e., resource allocation and service provisioning are dynamic and flexible. This is ensured by applying virtualization and SDN techniques. We model price-related decisions of customers and providers in this market: for customers, we show how they formalize their requirements, and how they select the suitable allocation from the resource offerings. For providers, we model how they relate to each other, and we derive how they should set their prices, given the expected characteristics of forthcoming customer demand. We use graph, probability and game theoretical models.

The presented work is pioneer in the analysis of pricing of multi-administrative heterogeneous resource providers. We prove that resource orchestration is a hard problem for customers due to the joint economic-technological requirements. Our results show that dynamic pricing on the other hand is well-suited to the nature of the traded resources. Furthermore, besides the expectation of the customer demand, the relative location of provider resources is of paramount importance in determining income-maximizing prices. We show in particular that those data center providers who are closer to the customer can set higher prices, and in turn the closer a network provider is to data centers, the higher its price is. The analysis presented in this paper has the potential to steer NFV orchestration solutions and the structure of provider federations, both being crucial in the realization of the 5G vision.