Hydrodynamic Quantum Field Theory: The Onset of Particle Motion and the Form of the Pilot Wave
- Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA, United States
We consider the hydrodynamic quantum field theory proposed by Dagan and Bush, a model of quantum dynamics inspired by Louis de Broglie and informed by the hydrodynamic pilot-wave system discovered by Couder and Fort. According to this theory, a quantum particle has an internal vibration at twice the Compton frequency that generates disturbances in an ambient scalar field, the result being self-propulsion of the particle through a resonant interaction with its pilot-wave field. Particular attention is given here to providing theoretical rationale for the geometric form of the wave field generated by steady, rectilinear particle motion at a prescribed speed, where signatures of both the de Broglie and Compton wavelengths are generally evident. While focus is given to the one-dimensional geometry considered by Dagan and Bush, we also deduce the form of the pilot wave in two dimensions. We further consider the influence on the pilot-wave form of the details of the particle-induced wave generation, specifically the spatial extent and vibration frequency of the particle. Finally, guided by analogous theoretical descriptions of the hydrodynamic system, we recast the particle dynamics in terms of an integro-differential trajectory equation. Analysis of this equation in the non-relativistic limit reveals a critical wave-particle coupling parameter, above which the particle self-propels. Our results provide the foundation for subsequent theoretical investigations of hydrodynamic quantum field theory, including the stability analysis of various dynamical states.
1. Introduction
In his double-solution pilot-wave theory [1–4], Louis de Broglie proposed a physical picture of quantum dynamics, according to which quantum particles move in concert with a guiding or “pilot” wave. In its rest frame, a particle of mass m0 was imagined to have an associated vibration at a frequency prescribed by the Einstein-de Broglie relation, , an internal clock with the Compton frequency, , where ℏ = h/(2π) is the reduced Planck constant and c the speed of light. This vibration was imagined to be responsible for generating a wave form, the particle's “pilot wave,” ϕ, responsible for propelling the particle. It was hoped, though never demonstrated, that the resulting particle dynamics would give rise to statistical behavior consistent with the predictions of the standard quantum formalism, as described by the wavefunction, Ψ. Owing to the distinct forms of ϕ and Ψ in de Broglie's original conception, this is widely referred to as his double-solution pilot-wave theory [5].
De Broglie's theory had a number of successes, including the Einstein-de Broglie relation, the de Broglie relation, p = ℏkB, between particle momentum, p, and its associated wavenumber, kB, and his prediction of electron diffraction, the experimental confirmation of which [6] earned him the Nobel Prize in 1929. Nevertheless, his double-solution theory was incomplete on several fronts [5]. First, he did not specify the physical nature of the pilot wave. Second, he failed to specify either the mechanism for pilot-wave generation or its resulting form. Initially, he posited that the pilot wave be monochromatic, from which p = ℏkB follows directly. Subsequently, he followed the lead of Bohm [7, 8] in asserting that the pilot wave, ϕ, is linearly related to the wavefunction, Ψ. This concession was made with the caveat that there is an unspecified singularity in ϕ in the vicinity of the particle; however, it otherwise reduced de Broglie's double-solution theory to Bohmian mechanics, hence, the two are often conflated into the so-called ‘de Broglie-Bohm’ theory. In Bohmian mechanics, the mechanism for pilot-wave generation is also absent: particles move in response to both the classical potential and the quantum potential, whose form is uniquely prescribed by the wavefunction, Ψ. The possibility of the particle playing a more active role, specifically acting as the source of its own pilot wave as originally proposed by de Broglie, was discussed by Holland [9].
The most substantial efforts to extend de Broglie's mechanics have come from workers in stochastic electrodynamics (also known as SED) [10, 11], according to which de Broglie's pilot wave may be sought in the electromagnetic quantum vacuum field [12, 13]. The geometry of the pilot-wave field in SED is relatively difficult to characterize, as it requires consideration of the vector electromagnetic field. Nevertheless, de la Peña and Cetto [10] assert that the de Broglie wave may be understood in terms of the Lorentz-transformed Doppler shifting of a pilot wave with the Compton frequency. Kracklauer [14] also speculated as to the form of the pilot wave in SED. We here adopt a simpler approach by following de Broglie in assuming that the pilot wave may be characterized in terms of a single scalar field. Doing so allows us to characterize the form of the resulting pilot-wave field, and so make clear the geometric significance of the de Broglie and Compton wavelengths on its structure.
In the hydrodynamic pilot-wave system discovered by Couder et al. [15], a bouncing droplet self-propels along the surface of a vertically vibrating fluid, guided by the pilot-wave form generated by its resonant interaction with the bath. This pilot wave is the superposition of two distinct wave forms generated at each impact: a traveling disturbance propagating radially outward from each impact, and an axisymmetric standing Faraday wave form centered on the point of impact [16]. The spatio-temporal extent of both the propagating and stationary wave forms is limited by the fluid viscosity. Consequently, the number of prior impacts that influence the droplet is limited by viscous damping. The most striking quantum features arise in the limit of weak viscous damping, also referred to as the “high-memory” limit, where the critical non-Markovian nature of the droplet dynamics is most pronounced [17]. In this limit, the walking droplet is dressed by a quasi-monochromatic wave form with the Faraday wavelength; the pilot wave propagates with the particle, as may be seen by strobing the system at the Faraday frequency [18]. The quantum-like features of the system emerge owing to the quasi-monochromatic form of the pilot wave deduced by superposing the standing wave forms generated at impact, and are only weakly influenced by the traveling waves [17].
Informed by the walking-droplet system, Dagan and Bush [19] presented a model of quantum dynamics, the so-called hydrodynamic quantum field theory (henceforth HQFT), inspired by de Broglie's double-solution pilot-wave theory [1, 4]. Specifically, they adopted de Broglie's notion that quantum particles have an internal clock, a vibration at the Compton frequency that interacts with a scalar background field that satisfies the Klein-Gordon equation. To describe the particle propulsion, de Broglie considered a guidance equation in which the particle velocity is proportional to the gradient of the phase of the monochromatic guiding wave. Dagan and Bush [19] explored a variant of this guidance equation, according to which the particle moves at a velocity proportional to the gradient of the pilot wave. As de Broglie did not specify the precise manner in which the particle vibration generates its associated pilot wave, Dagan and Bush [19] followed the physical analogy between pilot-wave hydrodynamics and de Broglie's mechanics proposed by Bush [20]. Specifically, they considered particle vibration at 2ωc to serve as a localized disturbance, acting over the scale of the Compton wavelength, λc = h/(m0c), of a scalar field, ϕ, that evolves according to the Klein-Gordon equation.
Dagan and Bush [19] restricted their attention to a one-dimensional geometry: the particle motion was restricted to a line. Nevertheless, their simulations revealed two striking features. First, the particle moves in concert with its pilot wave in such a way that its mean momentum satisfies the de Broglie relation, p = ℏkB. Second, the free particle is characterized by in-line speed oscillations at the frequency ckB, over a length scale comparable to the de Broglie wavelength. Here, we shall rationalize the emergence of the de Broglie relation by elucidating the precise form of the wave field in the immediate vicinity of the particle.
In the special case of prescribed particle motion at a constant speed, the simulations of Dagan and Bush [19] also indicated the form of the emergent pilot-wave field, which had two salient features. First, the leading and trailing forms were significantly different. Second, the relative prominence of the de Broglie and Compton wavelengths was seen to depend markedly on the particle speed. These two features, and their analogs arising for a two-dimensional pilot wave, will be rationalized through the theoretical developments presented herein. Finally, our theoretical developments allow us to derive an integro-differential trajectory equation for the particle motion, which we analyze in the non-relativistic limit. As in the hydrodynamic system, this integro-differential form will provide the theoretical basis for examining the stability of various dynamical states, including the in-line speed oscillations of the free particle reported by Dagan and Bush [19].
This paper is arranged as follows: In section 2, we review the theoretical model proposed by Dagan and Bush [19]. We also highlight a number of fundamental features of the Klein-Gordon equation that form the foundations of our analysis. In section 3, we derive an analytic solution of the pilot wave for the kinematic case of steady particle motion at a prescribed speed. Particular attention is given to rationalizing the salient features reported by Dagan and Bush [19]. Our theoretical developments are then extended to describe the two-dimensional pilot wave generated by rectilinear particle motion in the plane. Finally, in section 4, we derive an integro-differential trajectory equation for the particle motion, analysis of which indicates the onset of self-propulsion for sufficiently strong wave-particle coupling. This trajectory equation represents the starting point for future investigations of this new pilot-wave system.
2. Hydrodynamic Quantum Field Theory
2.1. Formulation
We examine the model of one-dimensional quantum dynamics proposed by Dagan and Bush [19], according to which the pilot wave, ϕ(x, t), and particle position, xp(t), evolve according to:
where primes denote differentiation with respect to time, t, and ϕ satisfies ϕ → 0 as x → ±∞. The pilot wave, ϕ(x, t), evolves according to the Klein-Gordon equation subject to a localized, periodic forcing, and the particle moves in response to the local gradient of its pilot-wave field. We note that the novelty of HQFT is the wave-particle coupling, as manifest in the forcing of the Klein-Gordon equation and the particle trajectory equation. It is this coupling that distinguishes our work from the numerous studies of the Klein-Gordon equation with a potential [21, 22]. The strength of the wave-particle coupling is governed by the free parameter α. The standard Lorentz factor is defined in terms of the particle velocity, , via γ(v) = (1 − (v/c)2)−1/2. We define , where ϕ0 is a characteristic value of ϕ and kc = 2π/λc is the Compton wavenumber. We recall that the Compton wavelength, λc, is the distance light travels in one Compton period, τc = 2π/ωc; thus, λc = cτc and ωc = ckc.
Following the suggestion of Schrödinger [23], and in order to achieve wave-particle resonance, Dagan and Bush [19] considered the special case of particle vibration at twice the Compton frequency, f(t) = sin(2ωct). They further localized the influence of the particle-induced forcing to the Compton wavelength by choosing
with a = λc/2. For the numerical examples presented herein, we adopt these two forms; however, we note that our analysis is not specific to these forms. In section 3, we investigate the influence of the forms of f(t) and g(x) on the resultant pilot wave. Specifically, we consider a more general periodic vibration, f(t), with dominant angular frequency ω0, and g(x) corresponding to any symmetric function exhibiting a peak about x = 0 and decaying as |x| → ∞, normalized such that .
2.2. The Klein-Gordon Equation
To aid our analysis of the periodically-forced Klein-Gordon equation (Equation 1a), we first recall some of the fundamental features of the unforced Klein-Gordon equation,
The term in Equation (3) renders this wave equation dispersive: the propagation speed of a wave depends on its wavelength. This dispersion relation is derived through consideration of traveling wave solutions to Equation (3) of the form ϕ(x, t) = ei(ωt−kx), where i is the imaginary unit. (As the wave form is unchanged under the mapping ω → −ω and k → −k, we consider ω > 0 without loss of generality). We thus obtain the dispersion relation
which relates the wave angular frequency, ω, and the wavenumber, k.
Since the group velocity, , increases monotonically from −c to +c as k is increased, for any prescribed particle velocity, v ∈ (−c, c), there is a unique wavenumber satisfying . This wavenumber is precisely the de Broglie wavenumber, kB(v), defined as
As such, the particle is accompanied by a moving wave packet with wavelength λB = 2π/|kB| in the vicinity of the particle. We note that the de Broglie wavelength, λB, and the Compton wavelength, λc, differ in general, but are identical when the particle speed is such that . The dependence of kB on the particle velocity, v, is illustrated in Figure 1, where asymptotes are evident as the particle speed approaches the speed of light. Notably, the de Broglie wavelength is infinite for a stationary particle. Finally, we remark that the phase speed,
is superluminal for any wavenumber, k; in particular, the de Broglie phase speed is . However, as the propagating crests do not carry energy, the principle of relativity is not violated.
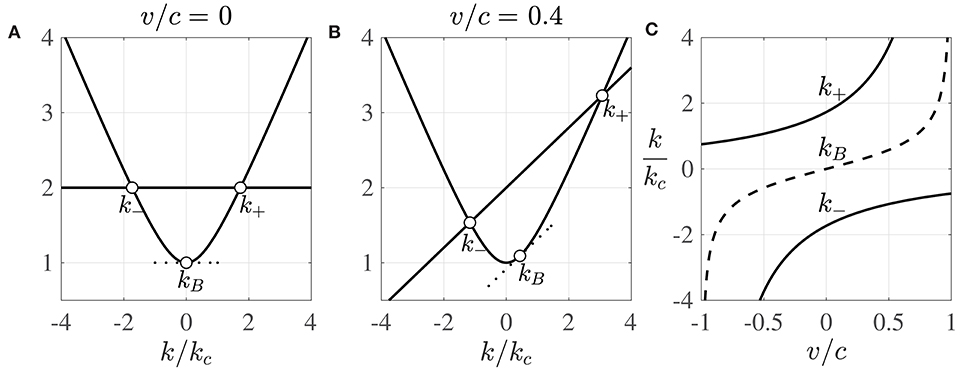
Figure 1. The wavenumbers excited by a particle moving at a prescribed, constant velocity, v, and vibrating at an angular frequency ω0 = 2ωc. Here kB is the de Broglie wavenumber (Equation 4) and k± are the wavenumbers of the traveling waves [see Equation (9)]. (A,B) The curve and line (ω0+kv)/ωc intersect at k+ > 0 and k− < 0, and have equal slope at kB. The dotted line also has slope v/ωc. (A) v/c = 0. (B) v/c = 0.4. (C) Dependence of k± (solid curves) and kB (dashed curve) on v.
2.3. The Form of the Pilot Wave
Dagan and Bush [19] considered two forms of particle motion: kinematics, in which the particle motion is prescribed as steady translation at a fixed velocity, v; and dynamics, where the particle is free to move in response to the gradient of the pilot wave according to Equation (1b). Our study of the pilot wave, ϕ, is similarly split into consideration of particle kinematics (section 3) and particle dynamics (section 4).
To demonstrate the richness and variety in the form of the pilot wave, we present snapshots of ϕ(x, t) for particle kinematics in Figure 2. These wave forms are similar to those deduced numerically by Dagan and Bush [19] and possess a number of intriguing features. First, there is a clear manifestation of the de Broglie wavelength, λB, most visible in advance of the particle: however, upon closer inspection, this wavelength modulates weakly in space, as is most apparent in Figure 2A, and the amplitude of this wave decreases as the particle speed increases. Second, we see the emergence of an additional wavelength, comparable (but not equal) to the Compton wavelength, λc. Such waves are visible only in the wake of the particle, and the amplitude of these waves increases with particle speed. We proceed by rationalizing these wave forms through a systematic theoretical analysis of the periodically-forced, one-dimensional Klein-Gordon equation, before demonstrating numerically that these salient features are also apparent in two dimensions.
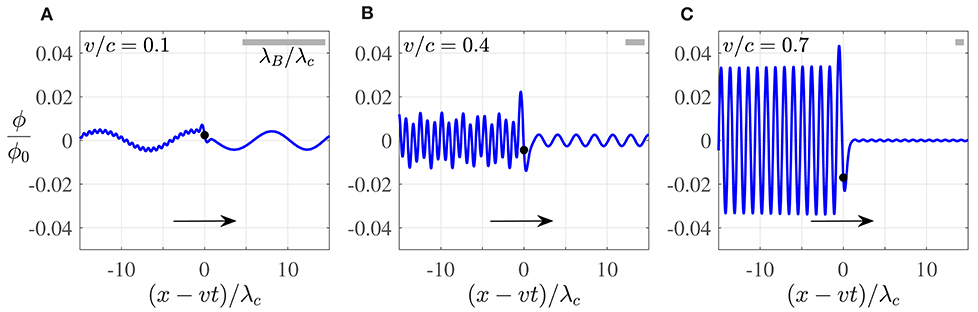
Figure 2. Snapshots of the pilot wave, ϕ, generated by a particle (black dot) moving at a prescribed velocity, v, such that (A) v/c = 0.1, (B) v/c = 0.4, (C) v/c = 0.7. The wave field oscillates in time and is sampled at t/τc = 600. The arrow denotes the direction of particle motion. The gray bar (top right of each panel) indicates the ratio λB/λc, which decreases as the particle speed increases, in accord with Equation (4). The solution was found analytically via a Fourier transform on an infinite domain (see Appendix 1), where the inversion was performed numerically using a Gauss-Kronrod quadrature routine built into MATLAB.
3. Pilot-Wave Kinematics
We first consider the kinematic case in which particle motion is prescribed, so we need not consider the partial trajectory equation (Equation 1b). Specifically, we consider the particle trajectory xp(t) = vt, where v > 0 corresponds to motion in the x-direction. The form of the pilot-wave field is thus described by the periodically-forced Klein-Gordon equation,
Example wave forms are presented in Figure 2. We consider the initial conditions ϕ = ∂t ϕ = 0 at t = 0 (for all x) and explore the dynamics of the waves generated in the vicinity of the particle after a long time. Our analysis in sections 3.1 and 3.2 is for a one-dimensional wave form. In section 3.4, we demonstrate that the salient features of the one-dimensional pilot wave persist in two dimensions. For simplicity, we consider the forcing f(t) = sin(ω0t) in the following analysis, but the wave form for a more general periodic forcing may be derived similarly through the linear superposition of the harmonics nω0, for any integer n. Our analysis coincides with the simulations of Dagan and Bush [19] for ω0 = 2ωc.
As the Klein-Gordon equation is linear, we decompose the solution of Equation (5) into two parts: the time-periodic particular solution, ϕp, which arises due to the periodic particle forcing; and the homogeneous solution, ϕh, whose initial wave form is chosen so that, when combined with the particular solution, the initial conditions for ϕ = ϕp + ϕh are satisfied. Our analysis reveals that the particular solution gives rise to emitted waves that propagate away from the particle, where the wavelengths in advance of and behind the particle differ and depend on the particle speed. However, both the leading and trailing propagating waves oscillate with the angular frequency, ω0, of the particle vibration. The homogeneous solution appears as a slowly decaying carrier wave whose local wavelength and angular frequency in the vicinity of the particle are precisely the de Broglie wavelength, λB, and the reduced angular frequency ωc/γ. In general, the propagating and carrier waves thus oscillate at different frequencies.
3.1. The Propagating Waves
We first derive the particular solution, ϕp, to the periodically-forced Klein-Gordon equation (Equation 5) for a prescribed particle velocity, v. To allow for generality in the spatial form, g(x), we first seek the Green's function, , satisfying
where δ(x) is the Dirac delta function, yielding the following spatial convolution for ϕp:
We find that this particular solution corresponds to emitted plane waves that propagate away from the moving particle, and that the form of g(x) determines the far-field amplitude of these waves.
To derive , we first consider periodic solutions to the unforced Klein-Gordon equation (Equation 3) of the form
In the frame of reference moving with the particle, the angular frequency shifts according to ω ↦ ω + kv, yielding the dispersion relation
When the angular frequency is that of the vibrating particle, ω = ω0, Equation (8) yields two corresponding wavenumbers,
The dependence of k± on the particle velocity, v, is presented in Figure 1 for the special case of ω0 = 2ωc considered by Dagan and Bush [19].
We now utilize the dispersion relation (Equation 8) in order to determine the wave forms of the particular solution, ϕp, when the angular frequency of the particle vibration exceeds the Compton angular frequency, ω0 > ωc, which encompasses the special case ω0 = 2ωc explored by Dagan and Bush [19]. (We shall demonstrate in section 3.3 that unphysical wave forms arise in the case of ω0 ≤ ωc). Equation (9) indicates that k+ > 0, corresponding to wave propagation in the positive x-direction, while k− < 0, corresponding to wave propagation in the negative x-direction. It thus follows that, for the case of v > 0 considered here, the leading and trailing wavenumbers are k+ and k−, respectively. Moreover, as k+ > |k−| for v > 0, the trailing wavelength is longer than the leading wavelength, a feature characteristic of a Doppler shift. Finally, we note that the phase speed, ω0/|k±|, of these propagating waves is comparable, but not precisely equal, to the de Broglie phase speed, , as was evident in the simulations of Dagan and Bush [19].
We demand that the waves propagate away from the vibrating particle. This radiation condition suggests that has the form
for x > vt. When x < vt, the form is similar, but k+ is replaced by k− (and similarly for A+ and B+). The coefficients, A± and B±, are determined by the assumed continuity of at x = vt and the jump condition
which follows from (6). The Green's function is then
where K = k+ for x > vt and K = k− for x < vt.
For a stationary particle (v = 0), Equation (9) determines k± = ±k0 (where ) and the Green's function (Equation 10) reduces to
Since k0 ≠ kc, the wavelength of the propagating waves differs from the Compton wavelength. Instead, k0 depends on the vibrational angular frequency, ω0. For the special case of interest, ω0 = 2ωc, the propagating waves are shorter than the Compton wavelength, with .
When the particle moves at a constant speed, symmetry is broken and the propagating waves exhibit a Doppler shift: shorter waves propagate ahead of the particle and longer waves are emitted in its wake. Since k+/kc → ∞ as v → c, we conclude that waves ahead of the particle are further compressed as the particle speed increases. Conversely, the waves behind the particle are stretched: the wavelength λ− = 2π/|k−| has the limiting form
In the special case of interest, ω0 = 2ωc, the far-field wavelength behind the particle approaches 4λc/3 in this limit.
The effect of the convolution (Equation 7) is to diminish rapid spatial oscillations arising in Equation (10). We define the Fourier transform of g(x) as
where the symmetry of g(x) implies that ĝ is a real and even function of k. Combining Equations (7) and (11), and applying the convolution theorem, reveals that, far from the particle, the trailing (−) and leading (+) propagating waves are approximated by
for v > 0, since is sinusoidal and g(x) acts over a localized region in space. For the case where g(x) is a Gaussian function [19], ĝ(k) is also a Gaussian; thus, short waves are diminished in amplitude to a greater extent than long waves. The amplitude of ϕp is thus less ahead of the particle, where waves are shorter, than in its wake, where waves are longer, as is evident in Figure 3.
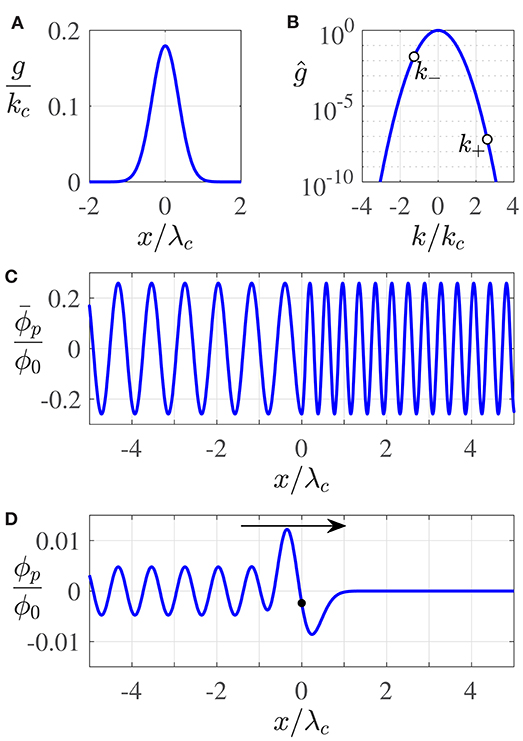
Figure 3. The propagating waves. (A,B) The Gaussian shape function, g(x), defined in (2), and its Fourier transform, ĝ(k) = e−a2k2/4. (C) The Green's function, , at t = 0 for v/c = 0.3. (D) The particular solution, , yields the form of the propagating waves at t = 0. The arrow denotes the direction of particle motion. The white circles in (B) at k = k± determine the trailing (−) and leading (+) wavelength of , where far from the particle.
3.2. The Carrier Wave
We now deduce the accompanying homogeneous solution, ϕh(x, t), to Equation (5), from which we demonstrate that the de Broglie wavelength is the local wavelength of a carrier wave propagating at the particle speed. As shown in Appendix 1, the homogeneous solution, ϕh, may be expressed as the inverse Fourier transform
where the functions a(k) and b(k) are defined in Appendix 1. Evaluating this integral analytically is intractable. However, we may proceed by exploiting the highly oscillatory form of the integrand for ωct ≫ 1 in order to derive the integral's asymptotic behavior using the method of stationary phase [24], as outlined in Appendix 2. By applying this asymptotic procedure to Equation (12), we obtain that the long-time form of the carrier wave is
an approximation valid for |x| < ct and ωct ≫ 1. The form of the slowly varying envelope, , depends only weakly on the particle speed [see Appendix 2].
We present the carrier wave, ϕh, in Figure 4, where its envelope, , may be seen to exhibit weak asymmetry about the origin. Notably, the wavelength of the carrier wave varies significantly in space, with compression ahead of the particle and elongation in its wake, characteristic of a Doppler shift. Moreover, we note that ϕh decays algebraically in time, so the significance of the carrier wave decreases as ωct → ∞. Nevertheless, this algebraic decay is sufficiently slow for the amplitude of ϕh to remain appreciable at finite time and so be evident in the pilot-wave forms presented in Figure 2.
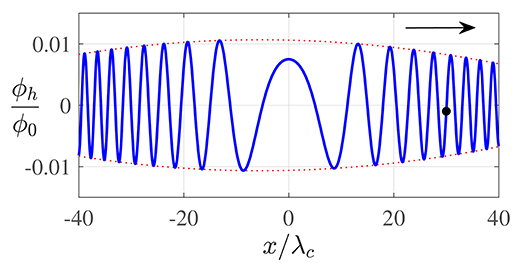
Figure 4. The carrier wave. The asymptotic homogeneous solution, ϕh [blue curve, see Equation (13)], for v/c = 0.3 and t/τc = 100, corresponding to a particle position xp/λc = 30 (black dot). In the vicinity of the particle, waves are contracted ahead of the particle and elongated behind it. The dotted curve denotes the slowly varying envelope, , where is defined in Appendix 2.
We now elucidate the manifestation of the de Broglie wavelength in the carrier wave, ϕh. For a particle moving with velocity v, we define χ = x − vt as the displacement from the particle. As the envelope, , is slowly varying, the dominant spatial oscillations in ϕh arise from the sinusoid in Equation (13), whose argument we expand in the vicinity of the particle (|χ/vt| ≪ 1). Specifically, we obtain
where the slowly varying wavenumber is
and kB is the de Broglie wavenumber (Equation 4). The first term on the right-hand side of Equation (14) corresponds to the temporal oscillation of the carrier wave at the reduced angular frequency ωc/γ. At the particle position (χ = 0), the local wavenumber, , of the carrier wave is precisely the de Broglie wavenumber, as might have been anticipated by the relationship [see Equation (4)]. Moreover, the local wavenumber varies slowly in space, as described by the correction term of size O(|χ/vt|) in Equation (15). This variation serves to compress the wavelength ahead of the particle and elongate it in the particle's wake (see Figures 2, 4). This wavenumber modulation decreases over time, and is also reduced for faster moving particles.
We may also infer why the local amplitude of the carrier wave decreases as the particle speed increases, a trend evident in Figure 2. We first recall from Equation (4) that |kB| increases with the particle speed. Moreover, the variations from the de Broglie wavelength in the vicinity of the particle become weaker as the particle speed increases, a trend due to the aforementioned correction term of size O(|χ/vt|). Consequently, there is a strong signature of the de Broglie wavelength in the vicinity of the particle, where the amplitude of this wave is governed by the value of ĝ(kB), akin to the dependence of the amplitude of the propagating waves on ĝ(k±) discussed in section 3.1. As |kB| increases with |v|, and ĝ(k) decreases with |k| (when g(x) is a Gaussian function), the local amplitude of the carrier wave is thus diminished with increasing particle speed, consistent with the trend apparent in Figure 2.
3.3. Summary
By combining the foregoing results, specifically superposing the propagating (Equation 7) and carrier (Equation 13) wave forms, we deduce that the one-dimensional wave form generated by particle motion at uniform speed is
an approximation valid for ωct ≫ 1 and |x| < ct. The Green's function, , is defined in Equation (10), and the envelope, , is defined in Appendix 2. As the asymptotic temporal decay of the carrier wave is algebraic, the signature of the de Broglie wavelength becomes imperceptible only at very large times. It is thus apparent why λB is evident in Figure 2 and the finite-duration simulations of Dagan and Bush [19], but is expected to vanish in the long-time limit.
In Figure 5, we present an example of the superposition ϕ = ϕp + ϕh, representing the full pilot-wave field. The particular solution, ϕp, describes waves that propagate away from the moving particle, where the approximate trailing (−) and leading (+) form is for v > 0. The shorter propagating waves ahead of the particle are imperceptible, but the longer propagating waves in the particle's wake remain appreciable. The homogeneous solution, ϕh, represents a carrier wave exhibiting local wavelength contraction and elongation ahead of and behind the particle, respectively. At the particle position, the local wavelength of the carrier wave is precisely the de Broglie wavelength. The asymptotic approximation (Equation 16) of the full pilot-wave field, ϕ, is in excellent agreement with the numerical solution of Equation (5), lending credence to our analytic approach.
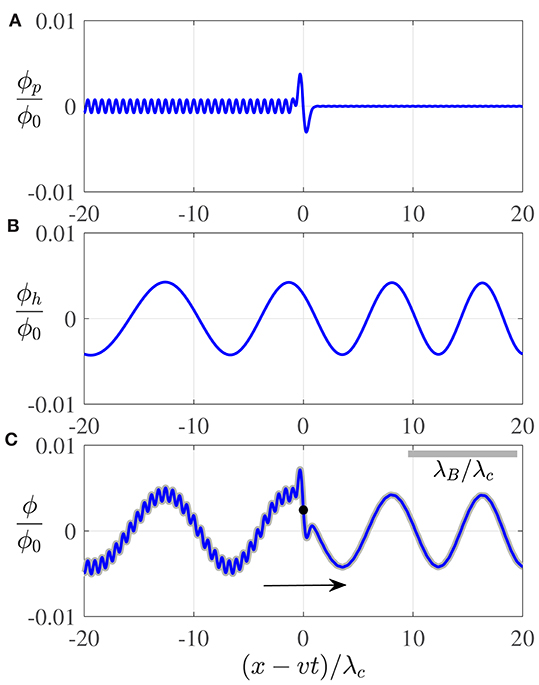
Figure 5. Wave forms accompanying a particle moving at constant velocity v = 0.1c after a time 600τc. (A) The analytic particular solution, ϕp [see Equations (7) and (10)], corresponding to propagating waves. (B) The long-time asymptotic approximation (Equation 13) of the homogeneous solution, ϕh, corresponding to the carrier wave. (C) The total wave field deduced analytically, ϕ = ϕp + ϕh (blue curve), coincides with the numerical solution (gray curve) shown in Figure 2A. The gray bar indicates the ratio λB/λc. The arrow indicates the direction of particle motion.
We proceed by examining the effects of changing the form of the spatial forcing, g(x). For Gaussian forcing of the form given in Equation (2), increasing the breadth, a, of the spatial forcing diminishes the amplitude of the propagating waves, ϕp, both ahead of and behind the moving particle, as the far-field wave amplitudes, , accordingly decrease due to the form ĝ(k) = e−a2k2/4. When the particle forcing is localized to a point (a → 0), we obtain , whose form, portrayed in Figure 3C, has leading and trailing propagating waves of equal amplitude. When g(x) is other than Gaussian, the far-field wave amplitudes, , may vary in a more complex manner as a function of the localization breadth, a, or particle speed, |v|. Nevertheless, since k+ → ∞ as v → c, and ĝ(k) → 0 as k → ∞, the amplitude of the propagating waves far ahead of the particle approaches zero as the particle speed approaches the speed of light.
We next examine the influence of the angular frequency, ω0, of the particle vibration, f(t) = sin(ω0t), on the form of the propagating waves. We first consider the case in which this frequency exceeds the Compton frequency, ω0 > ωc, which incorporates the case of resonant superharmonics of the form ω0 = nωc for integers n > 1. We recall that Dagan and Bush [19] restricted their attention to the case n = 2. As ω0 is increased, the wavenumbers k+ and k− both increase monotonically in magnitude [see Equation (9) and Figure 1], resulting in a decrease in the far-field amplitude of the propagating waves, . Consequently, the inclusion of higher harmonics results in a relatively small change in the form of the propagating waves, justifying the decision of Dagan and Bush [19] to consider only the superharmonic n = 2.
For the special case arising when the angular frequency of the particle vibration is equal to the Compton angular frequency, ω0 = ωc, it follows from Equation (9) that k− = 0 and k+ = 2γkB for v > 0. In this case, the wavelength of the propagating wave is infinite in the particle's wake and at most half the de Broglie wavelength in advance of the particle, giving rise to markedly different wave forms from those presented in Figures 2, 5. However, since k− = 0, the propagating waves generated in this special case of harmonic forcing exhibit the unphysical feature of an infinite-wavelength oscillation in the particle's wake.
Finally, we consider the case where the angular frequency of the particle vibration is less than the Compton angular frequency, ω0 < ωc, such as for the subharmonic vibration . Then, Equation (9) indicates that the wavenumbers k± are real for |v| > v*, where , and complex for |v| < v*. For fast-moving particles, |v| > v*, waves thus propagate ahead of the particle over two distinct length scales and no waves propagate in the particle's wake. Conversely, for slow-moving particles, |v| < v*, waves grow exponentially in space ahead of the particle (over a length scale determined by the imaginary part of k±), which renders the case ω0 < ωc unsuitable for the generation of a finite-amplitude pilot wave.
As a caveat, we note that our analysis is only valid within the light cone: the particular solution, ϕp, extends beyond the light cone at any finite time since ϕp is sinusoidal in the far field. Our analytic results are therefore invalid beyond a distance O((c − |v|)t) from the particle. Nevertheless, since we are chiefly interested in the wave form in the vicinity of the particle, as is necessarily responsible for guiding the particle, this limitation does not undermine the key results of our study as they pertain to HQFT.
3.4. The Two-Dimensional Pilot Wave
The approach developed here may be extended to higher spatial dimensions. We do so here in order to briefly characterize the two-dimensional pilot wave emerging for rectilinear particle motion in the plane x = (x, y), with particle velocity v = (v, 0). We restrict our attention to the case of superharmonic forcing, ω0 = 2ωc. Notably, the salient features of the one-dimensional pilot wave, specifically the propagation of waves away from the particle and the emergence of the de Broglie wavelength in the carrier wave, persist in two dimensions. In Appendix 3, we analytically determine the two-dimensional wave form of the periodically-forced Klein-Gordon equation [the equivalent of Equation (5)] in Fourier space, before inverting back to physical space numerically.
Figures 6, 7 both indicate that, as in one dimension, two clear length scales emerge, comparable to the Compton and de Broglie wavelengths. The separation in scales between λc and λB is most evident at low speeds, consistent with Equation (4). Figure 6 illustrates the wave form in the transient case, for which the particle is initialized at the origin, where the carrier wave forms about the particle's initial position. For a stationary or slowly moving particle, the particle is surrounded by its pilot wave. However, for faster particles, the amplitude of the waves ahead of the particle is diminished, as is evident in Figure 6F. Figure 7 illustrates the long-time form of the pilot wave, composed of propagating waves of characteristic wavelength λc emitted by the particle, and a carrier wave of the de Broglie wavelength propagating at the particle speed. Notably, the carrier wave ahead of the particle approaches a plane wave with the de Broglie wavelength as ωct → ∞. A more extensive exploration of HQFT in two dimensions will be left for future consideration.
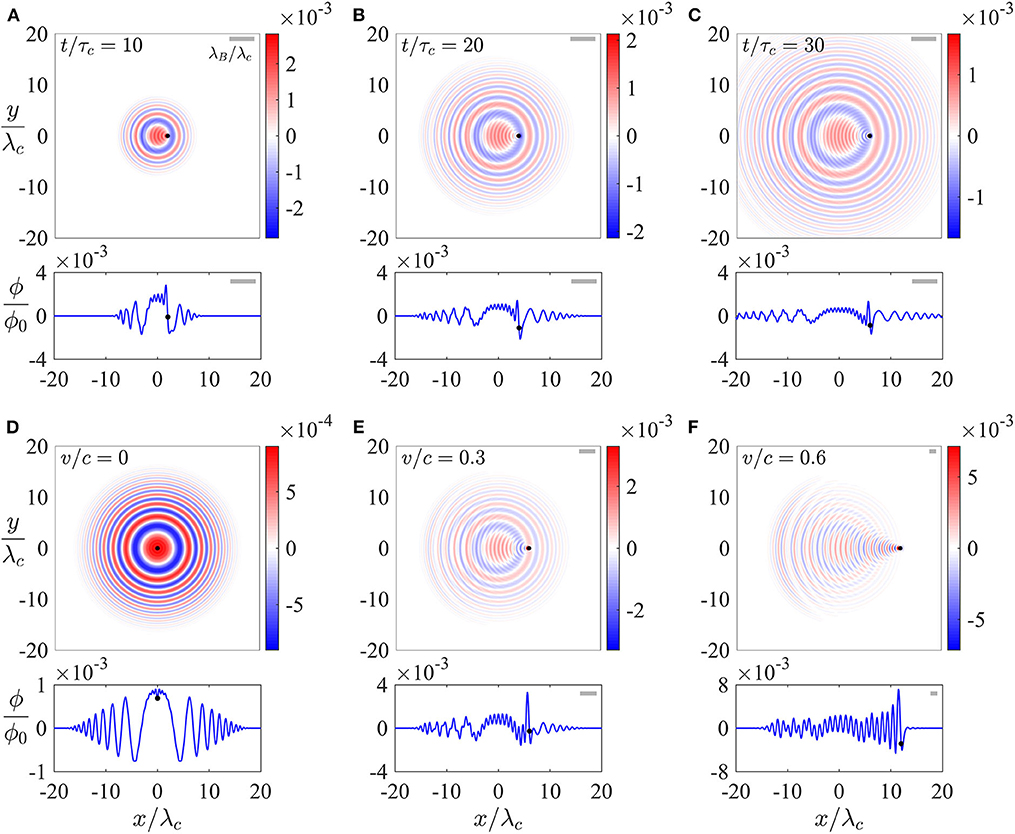
Figure 6. The two-dimensional wave forms generated by particle motion along the x-axis at a prescribed velocity, v = (v, 0), initiated at t = 0, when ϕ = ∂t ϕ = 0. The normalized wave amplitude, ϕ/ϕ0, is color-coded. The cross section of the wave form along the particle path (y = 0) is shown below. (A–C) A particle moves along the x-axis with v/c = 0.2, with snapshots at (A) t/τc = 10, (B) t/τc = 20, and (C) t/τc = 30. (D–F) The wave field generated at time t/τc = 20, where the propagation velocity is such that (D) v/c = 0, (E) v/c = 0.3, and (F) v/c = 0.6. The black dot denotes the particle position and the gray bar (top right of each panel) denotes λB/λc, which is necessarily infinite for v = 0. The wave forms were obtained by numerically inverting the Fourier transform solution of the two-dimensional periodically-forced Klein-Gordon equation, as described in Appendix 3.
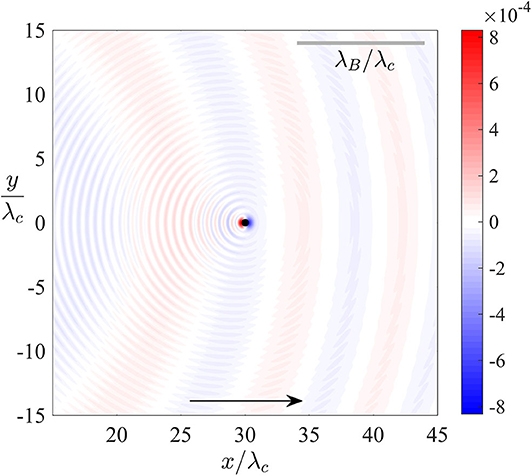
Figure 7. The two-dimensional pilot-wave field generated by particle (black dot) motion along the x-axis at a prescribed velocity, v = (0.1c, 0), after a time 300τc. The dimensionless wave amplitude, ϕ/ϕ0, is color-coded. Compton-scale propagating waves are evident in the particle's wake, and a de Broglie-scale, quasi-planar carrier wave propagates at the particle speed.
4. Pilot-Wave Dynamics
We proceed by transforming the coupled system (Equation 1) into an integro-differential trajectory equation governing the particle position. We do so by following Oza et al.'s [25] theoretical description of walking droplets, wherein the memory of the pilot-wave system is manifest in the wave force, and appears in the form of an integral over the particle path. This formulation has two principal benefits. First, the integro-differential equation provides a framework for mathematical analysis of the particle dynamics, including an assessment of the stability of various dynamical states. Second, since the influence of the pilot wave is felt only along the particle trajectory, one need not solve the Klein-Gordon equation numerically for all space, which will be particularly beneficial in higher dimensions. One may thus side-step the requirement of an increasingly large computational domain when the simulation duration is increased, a shortcoming of the numerical approach of Dagan and Bush [19]. We proceed by using the Green's function of the Klein-Gordon equation in order to derive a trajectory equation valid for arbitrary particle speed. We then simplify the resulting trajectory equation in the non-relativistic limit, |v| ≪ c. Analysis of the resulting dimensionless equation allows us to deduce the critical wave-particle coupling parameter required to support sustained particle self-propulsion.
4.1. The Green's Function
By definition, the Green's function, φ0(x, t), for the Klein-Gordon equation is the solution of
Its form may be determined exactly using standard analytic methods. To obtain the solution, ϕ(x, t), to the forced Klein-Gordon equation (Equation 1a), one then convolves (in space and time) φ0(x, t) with the right-hand side of Equation (1a). To side-step the complexity of the resulting double integral, we instead seek a modified Green's function (valid for ωct ≫ 1) that accounts for the form of the spatial forcing, allowing for a convolution in time only.
Specifically, we seek φ(x, t) satisfying
with . For initial conditions ϕ = ∂t ϕ = 0 at t = 0, the solution, ϕ(x, t), of (1a) is then given by the temporal convolution
where we have used translational invariance to recenter φ about the particle position.
To determine φ, we apply a Fourier transform in space to Equation (17), yielding an evolution equation for , specifically
with . This equation is readily solved, yielding
To obtain φ, we must then apply the inverse Fourier transform to : this process is simplified for ωct ≫ 1, where the highly oscillatory integrand may be approximated using the method of stationary phase [24], akin to the procedure outlined in Appendix 2. For |x| < ct, the asymptotic result is
where . At any given time, the local wavelength is longest at x = 0 and decreases as the light cone is approached (|x| → ct). Moreover, the function ĝ(k*) modulates the amplitude of the wave, and the decay of ĝ(k) as |k| → ∞ ensures that φ is not singular at |x| = ct.
To further simplify the form of φ, we recall that the Bessel function of the first kind with order zero has asymptotic form as |z| → ∞. As the large-argument decay of ĝ diminishes the amplitude of φ for |x| ≲ ct (see Figure 8), we may modify the asymptotic Green's function to the more tractable form
The validity of this approximation is demonstrated in Figure 8, where we see an excellent agreement between the evolution of the asymptotic and numerical forms of φ.
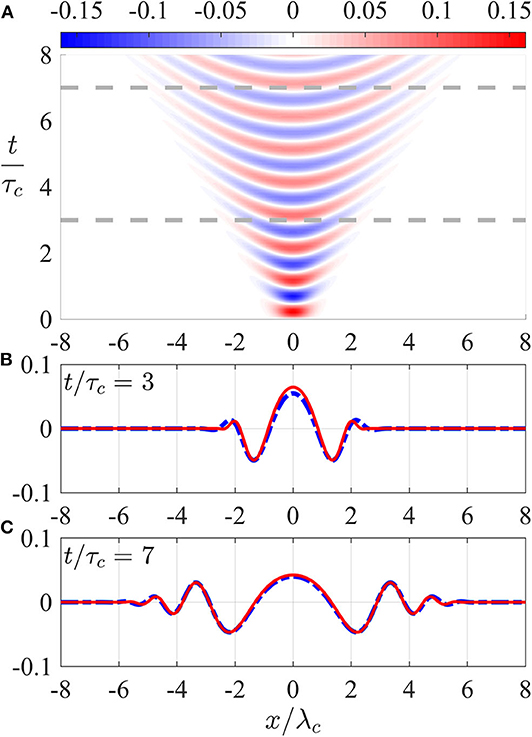
Figure 8. The Green's function. (A) Space-time wave evolution of φ, normalized by ϕ0 ωc, as computed numerically. The dashed lines correspond to the profiles presented in (B,C). (B,C) φ (blue dash-dotted curve) and its asymptotic approximation (Equation 19) (red solid curve) at times (B) t/τc = 3 and (C) t/τc = 7.
4.2. The Trajectory Equation
We proceed by combining Equations (1b), (18), and (19) in order to obtain the following integro-differential trajectory equation describing the evolution of the particle position, xp(t):
The only difference between this integral formulation (Equation 20) and the differential formulation (Equation 1) considered by Dagan and Bush [19] is the approximation of the Green's function, φ, by its asymptotic form (Equation 19). However, as in the stroboscopic model of walking droplets [25], the integral is extended to account for the particle's entire history, specifically its trajectory for t < 0.
We next derive a reduced trajectory equation, valid in the non-relativistic limit, in which for all time, t, where 0 < η ≪ 1. Equivalently,
for all time, t, and all s < t. To derive the non-relativistic trajectory equation, we expand Equation (20) in powers of η, where and
for |x/ct| ≪ 1. In this latter expansion, we have used the symmetry and normalization of g(x) to exploit that ĝ(k) ~ 1 + O(a2k2) for |ak| ≪ 1. As a result, the precise form of the localized particle forcing, g, only appears as a higher-order correction to the near-field slope of φ.
By combining the foregoing expansions and introducing the dimensionless variables , and , we reduce Equation (20) to the non-relativistic trajectory equation
where the resultant terms are all of size O(η) and we have neglected the correction terms of size O(η3). The dimensionless parameter, κ = αϵp/2c3, determines the strength of the wave-particle coupling, with larger κ resulting in higher particle speeds. We thus require κ > 0 to be sufficiently small that relativistic effects remain negligible. The non-relativistic trajectory equation (Equation 21) represents a convenient form for exploring non-relativistic pilot-wave dynamics in one dimension: We proceed by characterizing the onset of motion at the critical threshold κ = κc.
4.3. The Onset of Particle Motion
For the special case of superharmonic forcing, , we determine the critical wave-particle coupling parameter, κc > 0, beyond which the particle rest state, , is unstable and the system supports sustained particle self-propulsion. We first recast Equation (21) in the form
By noting that the coefficient of on the left-hand side is periodic with period π, we deduce that this linear trajectory equation is of Floquet form. We thus expect, and may verify numerically, that the onset of motion at κ = κc arises through lateral particle oscillation that is subharmonic relative to the particle's vibration, with a period of 2π corresponding precisely to the Compton period in our non-dimensionalization.
To determine κc, we expand using the Floquet ansatz
where the reality condition for is for all n, and * denotes complex conjugation. We substitute the Floquet ansatz (Equation 23) into (22) and evaluate the resultant integrals analytically, before grouping together powers of to form an infinite-dimensional system of equations for the unknown coefficients, Xn. The critical threshold, κc, is the value of κ at which the Xn coefficients have a non-trivial solution, for which the determinant of the corresponding matrix vanishes. Following the procedure outlined by Kumar and Tuckerman [26] and Kumar [27] for the study of the Faraday wave instability, we then truncate this system to a specified number of leading-order harmonics, at which we evaluate an approximation of κc numerically.
After substituting Equation (23) into (22), following the aforementioned procedure and evaluating integrals using the identity [28]
we obtain the infinite-dimensional, tridiagonal system
for all odd n, where We truncate this system to (N + 1) dimensions for the terms X−N, X−N+2, …, XN, where N ≥ 1 is an odd integer, and we set Xn = 0 for |n| > N. We define the corresponding critical threshold, κN, as the value of κ at which the truncated system is singular, where κN → κc ~ 2.97579… as N → ∞. Since a satisfactory approximation of κc is afforded by κ3 ~ 2.97894…, we deduce that the particle oscillation is dominated by the two leading-order harmonics, and , corresponding to lateral perturbations at ωc and 3ωc, respectively.
As may be confirmed numerically by direct simulation of Equation (22), the static state is stable for 0 < κ < κc and unstable for κ > κc. Similar lateral oscillations were observed in the simulations of Dagan and Bush [19], who described free particle motion in terms of lateral oscillations at the Compton frequency, superimposed on a slowly varying net drift. Our analytic results lend support to their inference that lateral oscillations at the Compton frequency are a fundamental feature of particle motion in HQFT. A fruitful avenue of future research may thus be to exploit the disparity between the time scale of particle translation and lateral oscillation, with a view to further simplifying the trajectory equation.
5. Discussion
The wave forms deduced herein have a number of striking similarities with those arising in pilot-wave hydrodynamics. The propagating waves arising in HQFT are similar to the traveling disturbances in the walker system, which typically play a relatively minor role in the hydrodynamic system, particularly in the guidance of a single droplet. In both systems, the moving particle is dressed in a quasi-monochromatic wave form, which has proven to be the critical feature for the emergence of quantum-like behavior in the hydrodynamic system [17, 20]. Both systems exhibit a Doppler shift, in which the pilot wavelength is compressed ahead of the moving particle, and elongated in the particle's wake [16, 29–31]. Strobing the carrier wave in the walking-droplet system at the Faraday frequency reveals a steady, quasi-monochromatic wave form with the Faraday wavelength, propagating with the droplet: strobing the carrier wave in HQFT at the reduced Compton angular frequency, ωc/γ, reveals a quasi-steady, quasi-monochromatic wave form with the de Broglie wavelength, propagating with the particle.
The wave forms explored herein also differ substantially from those arising in the walking-droplet system [15]. Most notably, the carrier waves in the two systems take markedly different forms. For rectilinear particle motion in HQFT, the carrier wave of local wavelength λB is centered on the particle's initial position (see Figure 6) and so may be considered as a relic of the initial conditions. However, in the vicinity of the particle, this carrier wave propagates at the particle speed, qualifying it as a viable candidate for a pilot wave in the fully dynamic treatment. In two spatial dimensions, the carrier wave approaches, in the long-time limit, a plane wave whose wavelength is precisely the de Broglie wavelength at the particle position. We note that a similar pilot-wave form was deduced by Andersen et al. [32], who described a quantum particle in terms of a wave packet solution to the forced Schrödinger equation subject to Galilean invariance. In the hydrodynamic system, the quasi-monochromatic carrier wave instead consists of the superposition of the stationary Faraday wave forms generated at each impact, giving rise to its characteristic horseshoe-like form [16]. Finally, the Faraday waves in the walker system decay exponentially in time owing to the influence of viscosity. In HQFT, the carrier wave is relatively long lived, exhibiting algebraic temporal decay; specifically, in one spatial dimension, the amplitude of the carrier wave decreases over time according to . One expects this relatively slow decay to result in a relatively pronounced influence of the particle's past trajectory on the instantaneous wave form in HQFT.
The dependence of the pilot-wave form on the particle speed elucidated here is both intriguing and encouraging. In the non-relativistic limit, the pilot-wave form is effectively monochromatic, with the de Broglie wavelength. Our analysis has shown that, in the special case of rectilinear motion, the carrier wave is a transient, dependent on the initialization of the system, and decays algebraically as ωct → ∞. While the form of this carrier wave was derived only for the special case of rectilinear particle motion at a prescribed speed, we anticipate that similar wave forms will arise for free particle dynamics [19]. Moreover, for different dynamical configurations, such as for in-line speed oscillations of the free particle [19] or orbital dynamics, the carrier wave form may in fact be more persistent than the case of rectilinear motion, producing a robust signature of the de Broglie wavelength in the pilot wave. The dynamics and emergent statistics might then be similar to those arising in pilot-wave hydrodynamics, where the Faraday wavelength plays a role analogous to the de Broglie wavelength in numerous settings, including orbital pilot-wave systems [33–36] and corrals [37, 38].
While the nonrelativistic trajectory equation (Equation 21) yields a convenient mathematical form, preliminary simulations have revealed that the particle has a propensity for speed fluctuations on the Compton time scale, at speeds approaching the speed of light [19]. These relativistic speed fluctuations are similar in form to the jittering modes arising in generalized pilot-wave hydrodynamics [39], the Zitterbewegung predicted in early models of quantum dynamics [23, 40], and the speed fluctuations evident in simulations of the free particle in HQFT [19]. Thus, while the mean particle speed may be slow relative to the speed of light, relativistic effects may still be significant on the Compton time scale, necessitating alternative simplifications of the relativistic trajectory equation (Equation 20). In the hydrodynamic system, one may average the droplet trajectory over one bouncing period, giving rise to a stroboscopic trajectory equation that requires no consideration of the droplet's vertical motion [25]. Analogous averaging of Equation (20) over the Compton period of lateral oscillations might give rise to a reduced trajectory equation for HQFT, similar in spirit to the stroboscopic model of pilot-wave hydrodynamics. Another potentially fruitful direction would be to consider the limit in which the intrinsic particle vibration, f(t), is characterized in terms of a periodically applied delta function. One might thus deduce a discrete-time iterative map similar in form to the hydrodynamic pilot-wave model of Durey Milewski [29].
Our theoretical developments have shown that, in the relativistic limit, |v| → c, the pilot-wave form is dominated by the Compton wavelength, suggesting the possibility of quantization arising on this scale. A tantalizing possibility thus presents itself of HQFT being able to capture structure on the scale of the Compton wavelength. For example, while hydrodynamic spin states are known to be unstable in the laboratory [41, 42], their analog in HQFT may correspond to the classical model of the electron, wherein a charge executes a circular orbit with the Compton frequency on a radius corresponding to the Compton wavelength [43]. HQFT thus promises the possibility of accounting for the emergence of both quantization and quantum statistics on the de Broglie wavelength for non-relativistic dynamics, and structure on the Compton scale for relativistic dynamics.
6. Conclusion
We have performed a detailed analysis of the one-dimensional pilot-wave model proposed by Dagan and Bush [19], an attempt to advance de Broglie's double-solution theoretical program [1–4] by exploiting insights gained from the walking-droplet system [15, 20]. Particular attention has been given to rationalizing the forms of the emergent pilot-wave fields reported by Dagan and Bush [19]. Our analysis has shown that the pilot wave is the combination of short, Compton-scale waves that propagate away from the moving particle, and a de Broglie-scale carrier wave. The wavelength of the carrier wave is precisely the de Broglie wavelength at the particle position, independent of the particle speed, which is consistent with the validity of the de Broglie relation, p = ℏkB. Moreover, in the vicinity of the particle, the frequency of the carrier wave is ωc/γ and the local wavelength exhibits a Doppler shift: this carrier wave thus has features of the pilot wave described by de la Peña and Cetto [10] in the context of stochastic electrodynamics. Notably, as the local wavelength is precisely the de Broglie wavelength, the gradient of the wave phase is simply proportional to the gradient of the wave amplitude, indicating that the wave-particle coupling considered by Dagan and Bush [19] is consistent with that proposed by de Broglie [1–4].
Our study of particle kinematics (section 3.3) has shown that increasing the spatial extent of the localized forcing of the particle on its pilot wave decreases the amplitude of both the propagating and carrier waves, thus presumably decreasing the efficacy of particle self-propulsion. Furthermore, the form of the pilot wave also varies significantly with the angular frequency, ω0, of the particle vibration. In the hydrodynamic system, resonance between the droplet's vertical motion and its subharmonic Faraday wave field is a prerequisite for a quasi-monochromatic wave field and the concomitant emergence of quantum-like behavior [17, 20]. We therefore expect that a similar resonance between particle and wave vibration will be necessary in HQFT: ω0 must be an integer multiple of ωc. Our deductions in section 3.3 indicate that the amplitude of the pilot wave is decreased when ω0 is large compared to ωc. To maximize the particle's propensity for self-propulsion, the choice ω0 = 2ωc considered by Dagan and Bush [19] thus appears to be the most propitious.
Finally, we have laid the foundations for deeper study of HQFT through the derivation of an integro-differential trajectory equation (Equation 20) similar in form to that derived for walking droplets [25, 44]. This formulation will enable more efficient simulation of the associated pilot-wave dynamics in a range of one-dimensional settings. Moreover, it will allow for the analysis of the stability of various dynamical states, including the free self-propelling state [19] and the oscillatory particle motion arising in the presence of a harmonic potential [45]. Of particular interest is the stability of the free self-propelling state to speed oscillations with the de Broglie wavelength [39], as may result in a commensurate statistical signature [46]. The extension of our analysis to two dimensions, as outlined in section 3.4, follows through a similar procedure, and has allowed for a comparison between the wave forms in HQFT and those arising in pilot-wave hydrodynamics. We expect the extension of HQFT to three dimensions to be straightforward, and to open up exciting new vistas in pilot-wave modeling.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Author Contributions
JB proposed the study. MD performed the mathematical analysis, numerical computations, and created the figures. All authors wrote the paper, gave final approval for publication, and agree to be held accountable for the work performed therein.
Funding
The authors gratefully acknowledge the NSF for financial support through grant CMMI-1727565.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge valuable discussions with, and input from, Yuval Dagan.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2020.00300/full#supplementary-material
References
1. de Broglie L. Recherches sur la thÉorie des Quanta. Migration-Université en Cours D'affectation (1924).
2. de Broglie L. An Introduction to the Study of Wave Mechanics. London, UK: Methuen, MA (1930). Available online at: https://catalog.hathitrust.org/Record/001477720
3. de Broglie L. The reinterpretation of wave mechanics. Found Phys. (1970) 1:1–15. doi: 10.1007/BF00708650
4. de Broglie L. Interpretation of quantum mechanics by the double solution theory. Ann Fond. (1987) 12:1–23.
5. Colin S, Durt T, Willox R. L. de Broglie's double solution program: 90 years later. Ann Fond Louis de Broglie. (2017) 42:19–71. Available online at: https://arxiv.org/pdf/1703.06158.pdf
6. Davisson CJ, Germer LH. Reflection of electrons by a crystal of nickel. Proc Natl Acad Sci USA. (1928) 14:317–22. doi: 10.1073/pnas.14.4.317
7. Bohm D. A suggested interpretation of the quantum theory in terms of “hidden” variables. I. Phys Rev. (1952) 85:166–79. doi: 10.1103/PhysRev.85.166
8. Bohm D. A suggested interpretation of the quantum theory in terms of “hidden” variables. II. Phys Rev. (1952) 85:180–93. doi: 10.1103/PhysRev.85.180
9. Holland PR. The Quantum Theory of Motion: An Account of the de Broglie-Bohm Causal Interpretation of Quantum Mechanics. Cambridge, MA: Cambridge University Press (2008).
10. de la Peña L, Cetto AM. The Quantum Dice: An Introduction to Stochastic Electrodynamics. Dordrecht: Kluwer Academic (1996). doi: 10.1007/978-94-015-8723-5
11. de la Peña L, Cetto AM, Valdés-Hernández A. The Emerging Quantum: The Physics Behind Quantum Mechanics. New York, NY: Springer (2015).
12. Boyer TH. Any classical description of nature requires classical electromagnetic zero-point radiation. Am J Phys. (2011) 79:1163–7. doi: 10.1119/1.3630939
13. Milonni PW. The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Cambridge, MA: Academic Press (1994). doi: 10.1016/B978-0-08-057149-2.50014-X
14. Kracklauer AF. Pilot-wave steerage: a mechanism and test. Found Phys Lett. (1999) 12:441–53. doi: 10.1023/A:1021629310707
15. Couder Y, Protiére S, Fort E, Boudaoud A. Walking and orbiting droplets. Nature. (2005) 437:208. doi: 10.1038/437208a
16. Eddi A, Sultan E, Moukhtar J, Fort E, Rossi M, Couder Y. Information stored in Faraday waves: the origin of a path memory. J Fluid Mech. (2011) 674:433–63. doi: 10.1017/S0022112011000176
17. Bush JWM, Couder Y, Gilet T, Milewski PA, Nachbin A. Introduction to focus issue on hydrodynamic quantum analogs. Chaos. (2018) 28:096001. doi: 10.1063/1.5055383
18. Harris DM, Bush JWM. The pilot-wave dynamics of walking droplets. Phys Fluids. (2013) 25:091112. doi: 10.1063/1.4820128
19. Dagan Y, Bush JWM. Hydrodynamic Quantum Field Theory: The Free Particle. Comptes Rendus Mécanique. (2020). doi: 10.5802/crmeca.34
20. Bush JWM. Pilot-wave hydrodynamics. Annu Rev Fluid Mech. (2015) 47:269–92. doi: 10.1146/annurev-fluid-010814-014506
21. Alhaidari AD, Bahlouli H, Al-Hasan A. Dirac and Klein-Gordon equations with equal scalar and vector potentials. Phys Lett A. (2006) 349:87–97. doi: 10.1016/j.physleta.2005.09.008
23. Schrödinger E. About the force-free motion in relativistic quantum mechanics. Prus Acad Sci. (1930) 31:418–28.
24. Bender CM, Orszag SA. Advanced Mathematical Methods for Scientists and Engineers I. New York, NY: Springer (1999). doi: 10.1007/978-1-4757-3069-2
25. Oza AU, Rosales RR, Bush JWM. A trajectory equation for walking droplets: hydrodynamic pilot-wave theory. J Fluid Mech. (2013) 737:552–70. doi: 10.1017/jfm.2013.581
26. Kumar K, Tuckerman LS. Parametric instability of the interface between two fluids. J Fluid Mech. (1994) 279:49–68. doi: 10.1017/S0022112094003812
27. Kumar K. Linear theory of Faraday instability in viscous fluids. Proc R Soc Lond A. (1996) 452:1113–26. doi: 10.1098/rspa.1996.0056
28. Abramowitz M, Stegun I. Handbook of Mathematical Functions. New York, NY: Dover Publications (1964).
29. Durey M, Milewski PA. Faraday wave-droplet dynamics: discrete-time analysis. J Fluid Mech. (2017) 821:296–329. doi: 10.1017/jfm.2017.235
30. Milewski PA, Galeano-Rios CA, Nachbin A, Bush JWM. Faraday pilot-wave dynamics: modelling and computation. J Fluid Mech. (2015) 778:361–88. doi: 10.1017/jfm.2015.386
31. Tadrist L, Shim JB, Gilet T, Schlagheck P. Faraday instability and subthreshold Faraday waves: surface waves emitted by walkers. J Fluid Mech. (2018) 848:906–45. doi: 10.1017/jfm.2018.358
32. Andersen A, Madsen J, Reichelt C, Rosenlund Ahl S, Lautrup B, Ellegaard C, et al. Double-slit experiment with single wave-driven particles and its relation to quantum mechanics. Phys Rev E. (2015) 92:013006. doi: 10.1103/PhysRevE.92.013006
33. Fort E, Eddi A, Boudaoud A, Moukhtar J, Couder Y. Path-memory induced quantization of classical orbits. Proc Natl Acad Sci USA. (2010) 107:17515–20. doi: 10.1073/pnas.1007386107
34. Harris DM, Bush JWM. Droplets walking in a rotating frame: from quantized orbits to multimodal statistics. J Fluid Mech. (2014) 739:444–64. doi: 10.1017/jfm.2013.627
35. Oza AU, Harris DM, Rosales RR, Bush JWM. Pilot-wave dynamics in a rotating frame: on the emergence of orbital quantization. J Fluid Mech. (2014) 744:404–29. doi: 10.1017/jfm.2014.50
36. Perrard S, Labousse M, Miskin M, Fort E, Couder Y. Self-organization into quantized eigenstates of a classical wave-driven particle. Nat Commun. (2014) 5:3219. doi: 10.1038/ncomms4219
37. Harris DM, Moukhtar J, Fort E, Couder Y, Bush JWM. Wavelike statistics from pilot-wave dynamics in a circular corral. Phys Rev E. (2013) 88:011001. doi: 10.1103/PhysRevE.88.011001
38. Sáenz PJ, Cristea-Platon T, Bush JWM. Statistical projection effects in a hydrodynamic pilot-wave system. Nat Phys. (2018) 14:315–9. doi: 10.1038/s41567-017-0003-x
39. Durey M, Turton SE, Bush JWM. Speed oscillations in classical pilot-wave dynamics. Proc R Soc A. (2020) 476:20190884. doi: 10.1098/rspa.2019.0884
40. Hestenes D. The zitterbewegung interpretation of quantum mechanics. Found Phys. (1990) 20:1213–32. doi: 10.1007/BF01889466
41. Labousse M, Perrard S, Couder Y, Fort E. Self-attraction into spinning eigenstates of a mobile wave source by its emission back-reaction. Phys Rev E. (2016) 94:042224. doi: 10.1103/PhysRevE.94.042224
42. Oza AU, Rosales RR, Bush JWM. Hydrodynamic spin states. Chaos. (2018) 28:096106. doi: 10.1063/1.5034134
43. Burinskii A. The Dirac-Kerr-Newman electron. Gravit Cosmol. (2008) 14:109–22. doi: 10.1134/S0202289308020011
44. Moláček J, Bush JWM. Drops walking on a vibrating bath: towards a hydrodynamic pilot-wave theory. J Fluid Mech. (2013) 727:612–47. doi: 10.1017/jfm.2013.280
45. Durey M, Milewski PA, Bush JWM. Dynamics, emergent statistics, and the mean-pilot-wave potential of walking droplets. Chaos. (2018) 28:096108. doi: 10.1063/1.5030639
Keywords: Klein-Gordon equation, de Broglie relation, matter waves, Compton scale, hydrodynamic quantum analogs
Citation: Durey M and Bush JWM (2020) Hydrodynamic Quantum Field Theory: The Onset of Particle Motion and the Form of the Pilot Wave. Front. Phys. 8:300. doi: 10.3389/fphy.2020.00300
Received: 25 April 2020; Accepted: 30 June 2020;
Published: 11 August 2020.
Edited by:
Ana Maria Cetto, Universidad Nacional Autónoma de México, MexicoReviewed by:
Catalina Stern, National Autonomous University of Mexico, MexicoSania Qureshi, Mehran University of Engineering and Technology, Pakistan
Copyright © 2020 Durey and Bush. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: John W. M. Bush, bush@math.mit.edu
 Matthew Durey
Matthew Durey John W. M. Bush
John W. M. Bush