1 Introduction

Insurance risk was originally studied in terms of ruin probability. This approach may, however, underestimate risk since insurance companies are realistically more interested in maximizing company value than minimizing risk and an alternative approach is therefore to study optimal dividend policies—in the sense of maximizing the expected value of the sum of discounted future dividend payments—as suggested by De Finetti in the 1950s; see De Finetti (1957). A vast literature on various versions of the optimal dividend problem has since emerged. Surveys of the topic include Albrecher and Thonhauser (2009), Avanzi (2009) and Taksar (2000); see also Alvarez (2018) and Schmidli (2008).

A common type of formulation of the optimal dividend problem corresponds to assuming that the only cash flow that may occur between the insurance company and its owner is from the insurance company to its owner, and in this formulation the insurance company typically goes bankrupt when the surplus process becomes negative; see e.g. De Finetti (1957), Jeanblanc-Picqué and Shiryaev (1995) and Shreve et al. (1984). In other words, the owner of the insurance company is not allowed to inject capital into the insurance company in this formulation of the problem. Another common type of formulation corresponds to assuming that the owner of the insurance company is obliged to inject capital so as to keep the surplus process non-negative; see e.g. Avram et al. (2007), Kulenko and Schmidli (2008) and Shreve et al. (1984). Hence, bankruptcy can never occur in this formulation of the problem. Further reviews of these two formulations of the optimal dividend problem can be found in Albrecher and Thonhauser (2009, Section 4) and Avanzi (2009, Section 5).

Corporations in financial and insurance markets in the real world, however, typically have the possibility of both going bankrupt and raising equity capital from its owner (capital injection). One of the first papers to take both of these market characteristics into account simultaneously is Løkka and Zervos (2008) which studies a singular stochastic control problem corresponding to the optimal dividend problem with the possibility of both capital injection and bankruptcy, under the assumption that the uncontrolled surplus process is a Wiener process with drift. The authors find that depending on the parameters of the model it is either optimal to pay dividends in order to reflect the surplus process at an upper barrier and never inject capital, or to pay dividends and inject capital in order to always reflect the surplus process at an upper barrier and at 0. The results of Løkka and Zervos (2008) are in Zhu and Yang (2016) extended to a general Itô diffusion model with a growth restriction for the drift function. In Gajek and Kuciński (2017) the optimal dividend problem with proportional costs for capital injection is studied under the assumption that the owner can at any time choose to liquidate the insurance company and thereby receive a liquidation value. The uncontrolled surplus process, which is defined as the surplus in excess of a parameter interpreted as a solvency capital requirement, follows a spectrally negative Lévy process.

Corporations in financial and insurance markets are also regulated by supervisory authorities. In order to take this characteristic into account (Paulsen 2003) studies the optimal dividend problem in a model with solvency constraints, meaning that it is not allowed to pay dividends unless the surplus process exceeds a given constant—in the present paper called dividend payout barrier. Capital injection is not considered. The author finds that it is optimal to use a reflection strategy with the reflection barrier being the maximum of the dividend payout barrier and the reflection barrier that would have been optimal without regulation. The uncontrolled surplus process is a fairly general Itô diffusion. The results of Paulsen (2003) are in He et al. (2008) extended by the introduction of the possibility of reinsurance. The optimal dividend problem has also been studied in the finance literature, where both Décamps et al. (2011) and Hugonnier and Morellec (2017) study models allowing for both bankruptcy and capital injection. In these papers there are fixed costs for capital injection, implying that the solutions involve lump sum, i.e. impulse control type, capital injections; Hugonnier and Morellec (2017) moreover consider a liquidation value and study liquidity and leverage requirements. The uncontrolled state process in Décamps et al. (2011) is a Wiener process with drift. The uncontrolled state process in Hugonnier and Morellec (2017) is a Wiener process with drift and exponentially distributed jumps.

In He and Liang (2009) both fixed and proportional transaction costs for capital injection, as well as reinsurance and bankruptcy are considered; the underlying model is a Wiener process with drift and there is no regulation. Other papers studying different models with capital injection and bankruptcy without regulation are Avanzi et al. (2011), Dai et al. (2010) and Zhu and Yang (2016). In Zhou and Yuen (2012) proportional reinsurance and a maximum dividend rate restriction are studied in a particular diffusion model; capital injection and the possibility of bankruptcy are studied separately. In Kulenko and Schmidli (2008) the classical Cramér–Lundberg model without bankruptcy is studied. A similar model with solvency constraints is studied in Zhang et al. (2010). In Avram et al. (2007) a spectrally negative Lévy process model without bankruptcy is considered. Other papers studying different models without bankruptcy are Paulsen (2008), Peng et al. (2012), Schmidli (2017), Sethi and Taksar (2002) and Yao et al. (2011). In Bai et al. (2012) an Itô diffusion model with fixed transaction costs and solvency constraints without capital injection is studied. In Chen et al. (2016) an optimal dividend problem with mandatory capital injection under time-inconsistent preferences is studied using the game-theoretic approach to time-inconsistent stochastic control; general references for this approach include Björk et al. (2017), Christensen and Lindensjö (2018), Christensen and Lindensjö (2020) and Lindensjö (2019). In De Angelis and Ekström (2017) and Grandits (2013) the dividend problem without capital injection is considered for a Wiener process with drift and a finite time horizon. We remark that further comparisons of the present paper to some of the references above are made in the sections below.

The present paper is organized as follows. In Sect. 2 we formulate the main problem which is a singular stochastic control problem allowing capital injection as well as bankruptcy under regulation of the dividend payout barrier type with proportional costs of capital injection. In Sect. 3 we formulate and solve two problems which are intimately connected to the main problem. In Sect. 4 we use the results of Sect. 3 to solve the main problem; the main result is Theorem 4.1. Section 4.1 contains graphical illustrations. In Sect. 5 we study an extension of our model by introducing the possibility for the owner to choose a stopping time at which the insurance company is liquidated and the owner obtains a liquidation value. Section 6 contains conclusions.

2 Problem formulation and preliminaries

Consider a filtered probability space \((\Omega ,\mathcal{F},\mathbb {P},\underline{\mathcal {F}})\) satisfying the usual conditions and supporting a Wiener process W. The controlled surplus process X of an insurance company is given by

$$\begin{aligned} X _t&= x + \mu t + \sigma W_t+C_t - D_t, \end{aligned}$$

where the process D corresponds to accumulated dividends paid to the owner of the insurance company and the process C corresponds to accumulated capital injection from the owner. The initial surplus satisfies \(x\ge 0\) and the parameters satisfy \(\mu >0\) and \(\sigma >0\). We suppose that for a given financing strategy (C, D) the value of the insurance company is the expected value of the sum of the discounted future cash flow to the owner and that the owner wants to maximize the value of the insurance company. In mathematical terms we thus consider the singular stochastic control problem

$$\begin{aligned} V(x;b_r)&:= \sup _{(C,D)\in \mathcal A(x,b_r)}\mathbb {E}_x\left( \limsup _{t\rightarrow \infty }\left( \int _0^{\tau \wedge t}e^{-\alpha s}dD_s -k\int _0^{\tau \wedge t}e^{-\alpha s}dC_s \right) \right) , \end{aligned}$$
(2.1)
$$\begin{aligned} \tau&:= \inf \{t\ge 0: X_t <0\}, \end{aligned}$$
(2.2)

where we interpret \(k>1\) as a proportional cost of injecting capital (equity issuance costs), \(\alpha >0\) as a discount rate, \(\tau \) as the random bankruptcy time and where \(\mathcal A(x,b_r)\) is the set of admissible strategies:

Definition 2.1

For a given initial surplus \(x\ge 0\) and dividend payout barrier \(b_r\ge 0\), a pair (C, D) is said to be an admissible strategy if C and D are non-decreasing LCRL \(\underline{\mathcal {F}}\)-adapted processes with \(C_0=D_0=0\) satisfying the dividend payout condition

$$\begin{aligned} \int _0^\tau I_{\{X_t <b_r\}}dD_t = 0 ~ \text{ a.s. } \end{aligned}$$
(2.3)

The main objective of the present paper is to study problem (2.1). This problem has according to the authors’ knowledge not been studied before.

Obviously the parameters of the model are such that either condition (2.4) below holds, or (2.4) holds with reversed inequality, which is interpreted as proportional costs of capital injection k being low or high, respectively. In Theorem 4.1 we will see that which is the case determines the kind of solution problem (2.1) has.

$$\begin{aligned} k&\le \frac{ r_1-r_2 }{ r_1 \left( \frac{r_2^2}{r_1^2}\right) ^{\frac{r_1}{r_1-r_2}} - r_2 \left( \frac{r_2^2}{r_1^2}\right) ^{\frac{r_2}{r_1-r_2}} } , \end{aligned}$$
(2.4)
$$\begin{aligned}&\text{ where } ~ r_1 := -\frac{\mu }{\sigma ^2} +\sqrt{\frac{\mu ^2}{\sigma ^4}+\frac{2\alpha }{\sigma ^2}}, ~ r_2 := -\frac{\mu }{\sigma ^2} -\sqrt{\frac{\mu ^2}{\sigma ^4}+\frac{2\alpha }{\sigma ^2}}. \end{aligned}$$
(2.5)
$$\begin{aligned}&\text{ Note } \text{ that } r_2< 0 < r_1\hbox { and }r_2^2>r_1^2. \end{aligned}$$
(2.6)

Remark 2.2

Formally we write \(dD_t=dD^c_t + \Delta D_t\) where \(D^c\) denotes the continuous part of D while \(\Delta D_t:= D_{t+}-D_t\), for \(D_{t+}:= \lim _{h\searrow 0}D_{t+h}\), denotes jumps in D. The processes C and X are treated analogously.

Remark 2.3

Condition (2.3) implies that if the surplus at time t is smaller than the dividend payout barrier \(b_r\) then dividends are not allowed, i.e. \(dD_t = 0\). Thus, if \(X_{t+}<b_r\) then a potential jump \(\Delta X_t\) cannot have been caused by D and must have been caused by C and hence \(X_t\le X_{t+}<b_r\), implying that \(dD_t = 0\) also in this case; in mathematical terms this means that (2.3) implies that

$$\begin{aligned} \int _0^\tau I_{\{X_{t+} <b_r\}}dD_t = 0 ~ \text{ a.s. } \end{aligned}$$

In other words, the surplus directly after a dividend payment cannot be lower than the dividend payout barrier \(b_r\) either.

Remark 2.4

An inequality analogous to that of (2.4) is used in Løkka and Zervos (2008) when studying problem (2.1) without the presence of a dividend payout barrier, i.e. with \(b_r=0\). Regulation of the type (2.3) was first studied in Paulsen (2003).

2.1 Preliminaries

Here we informally recall well-known results that are used throughout the present paper; cf. e.g. Karatzas and Shreve (1991), Pilipenko (2014) and Shreve et al. (1984). For any \(b>0\) and \(x \in [0,b]\) there exists an \(\underline{\mathcal {F}}\)-adapted non-decreasing continuous process \(\bar{D}^b\) with \(\bar{D}^b_0=0\) such that the process X defined by

$$\begin{aligned} X _t= x + \mu t + \sigma W_t - \bar{D}^b_t, \end{aligned}$$
(2.7)

is reflected at b and satisfies \( dX _t = \mu dt + \sigma dW_t\) when \(X_t<b\), with \(\bar{D}^{b}\) being constant on any interval where \(X_t<b\). There also exists a pair of \(\underline{\mathcal {F}}\)-adapted non-decreasing continuous processes \((C^0,D^b)\) with \(C^0_0=D^b_0=0\) such that the process X defined by

$$\begin{aligned} X _t= x + \mu t + \sigma W_t + C^0_t - D^b_t, \end{aligned}$$
(2.8)

is reflected at b and 0, and satisfies \(dX _t = \mu dt + \sigma dW_t\) when \(0<X_t<b\), with \(D^b\) being constant on any interval where \(X_t<b\) and \(C^0\) being constant on any interval where \(X_t>0\). In the case \(x>b\), \(\bar{D}^b\) and \(D^0\) are defined so that the corresponding processes in (2.7) and (2.8) jump from x to b at \(t=0\).

The pair \((C^0,D^b)\) is in the present paper said to be a double barrier strategy, while \((0,\bar{D}^b)\), or simply \(\bar{D}^b\), is said to be an upper barrier strategy. For an upper barrier strategy \(\bar{D}^b\) and \(\tau \) defined in (2.2), the value function \(x \mapsto \mathbb {E}_x\left( \int _0^{\tau } e^{-\alpha t}d\bar{D}_t^b\right) \) is the unique solution to

$$\begin{aligned} \alpha f(x)&= \mu f'(x) +\frac{1}{2} \sigma ^2 f''(x), ~ 0 \le x < b, \end{aligned}$$
(2.9)
$$\begin{aligned} f(x)&= x-b+ f(b), ~ x \ge b, \end{aligned}$$
(2.10)
$$\begin{aligned} f(0)&=0, ~ f'(b) = 1, \end{aligned}$$
(2.11)

cf. (Shreve et al. 1984, Lem. 2.1, Cor. 2.2 and Ex. 1). The general solution to the ODE (2.9) is, for \(r_1\) and \(r_2\) defined in (2.5) and constants \(c_1\) and \(c_2\),

$$\begin{aligned} f(x)&= c_1 e^{r_1x} + c_2 e^{r_2x}. \end{aligned}$$
(2.12)

The general solution together with (2.10) and the boundary conditions (2.11), and simple calculations, yield, for any \(b>0\),

$$\begin{aligned} \mathbb {E}_x\left( \int _0^{\tau } e^{-\alpha t}d\bar{D}_t^b\right) ={\left\{ \begin{array}{ll} \frac{e^{r_1 x}-e^{r_2 x}}{r_1e^{r_1 b}-r_2e^{r_2 b}}, &{}\quad 0 \le x \le b,\\ x-b+ \frac{e^{r_1 b}-e^{r_2 b}}{r_1e^{r_1 b}-r_2e^{r_2 b}}, &{}\quad x>b. \end{array}\right. } \end{aligned}$$
(2.13)

For a double barrier strategy \((C^0,D^b)\) the stopping time in (2.2) trivially satisfies \(\tau =\infty \) a.s. The value function \(x \mapsto \mathbb {E}_x\left( \int _0^{\infty } e^{-\alpha t}dD_t^b -k\int _0^{\infty } e^{-\alpha t}dC^0_t \right) \) with \(k>1\) is well-defined and is the unique solution to (2.9) together with (2.10) and the boundary conditions

$$\begin{aligned} f'(0)=k, ~ f'(b) = 1, \end{aligned}$$
(2.14)

cf. (Shreve et al. 1984, Lem. 2.1, Cor. 2.2 and Ex. 1). The general solution (2.12) together with (2.10) and (2.14) yield, for any \(b>0\),

$$\begin{aligned}&\mathbb {E}_x\left( \int _0^{\infty } e^{-\alpha t}dD_t^b -k\int _0^{\infty } e^{-\alpha t}dC^0_t \right) \nonumber \\&\quad ={\left\{ \begin{array}{ll} \frac{1}{e^{r_1b}-e^{r_2b}}\left( \frac{1-ke^{r_2b}}{r_1}e^{r_1 x}-\frac{1-ke^{r_1b}}{r_2}e^{r_2x}\right) , &{}\quad 0\le x \le b,\\ x-b+ \frac{1}{e^{r_1b}-e^{r_2b}}\left( \frac{1-ke^{r_2b}}{r_1}e^{r_1 b}-\frac{1-ke^{r_1b}}{r_2}e^{r_2b}\right) , &{}\quad x>b. \end{array}\right. } \end{aligned}$$
(2.15)

Remark 2.5

The process \(\bar{D}^b\) can be pathwise defined as \(\bar{D}^b_t=\max _{0\le s\le t}(x+\mu s+ \sigma W_s-b)_+\) which can be seen using the corresponding Skorokhod equation, cf. Asmussen and Taksar (1997) and (Karatzas and Shreve 1991, Section 3.6 C). The pair \((C^0,D^b)\) can be constructed pathwise in a procedure involving iteratively using the solutions to the Skorokhod equations for reflection at b and at 0 in turn, as noted in Løkka and Zervos (2008, p. 960).

3 Two restricted problems

In order to solve problem (2.1) it is useful to first study two related problems for which the set of admissible strategies is further restricted.

3.1 Capital injection not allowed

Here we consider problem (2.1) under the additional restriction that capital injection is not allowed—this problem has been studied in the literature, see Paulsen (2003), and we here only recall the solution. That is, we consider admissible strategies \((C,D) \in \mathcal A(x,b_r)\) for which

$$\begin{aligned} C_t =0 ~ \text{ for } \text{ all } t \ge 0 \text{ a.s. } \end{aligned}$$

For this restricted problem we can write, using also that D is non-decreasing, the optimal value function (2.1) as

$$\begin{aligned} \sup _{(0,D)\in \mathcal A(x,b_r)}\mathbb {E}_x\left( \int _0^{\tau } e^{-\alpha t}dD_t\right) . \end{aligned}$$
(3.1)

The solution to this problem is given by:

Theorem 3.1

The upper barrier strategy \(\bar{D}^{b}\) with \(b=b_r\vee b^{*}\) is optimal in (3.1), where

$$\begin{aligned} b^*:= \frac{\log \left( r_2^2/r_1^2\right) }{r_1-r_2}>0. \end{aligned}$$
(3.2)

Proof

The result can be proved using arguments similar to those in the proof of Theorem 4.1. The constant in (3.2) is also found in Shreve et al. (1984, Eq. (5.6)) and Løkka and Zervos (2008, Eq. (3.6)) see also Remark 3.3. Note that \(b^*>0\) by (2.6). The result also follows from Paulsen (2003, Theorem 2.2). \(\square \)

The value function corresponding to the strategy in Theorem 3.1 can, using the results of Sect. 2.1, be written as

$$\begin{aligned} G(x;b_r):={\left\{ \begin{array}{ll} \frac{e^{r_1 x}-e^{r_2 x}}{r_1e^{r_1 b}-r_2e^{r_2 b}}, &{}\quad 0 \le x \le b,\\ x-b+ \frac{e^{r_1 b}-e^{r_2 b}}{r_1e^{r_1 b}-r_2e^{r_2 b}}, &{}\quad x>b, ~ \text{ where } b=b_r\vee b^{*}. \end{array}\right. } \end{aligned}$$
(3.3)

We will typically write G(x) instead of \(G(x;b_r)\) for convenience. Lemma 3.2 presents properties of the function G that are used when solving problem (2.1) in Sect. 4.

Lemma 3.2

For G defined in (3.3) it holds that:

  1. (I)

    \(G'(x) > 0\) for all \(x\ge 0\).

  2. (II)

    If condition (2.4) holds with reversed inequality, then \(G'(0) \le k\).

Proof

We use (2.6) repeatedly. Item (I) is directly verified. Let us prove (II). We find

$$\begin{aligned} G'(0) = \frac{r_1-r_2}{r_1e^{r_1b} -r_2e^{r_2b} }. \end{aligned}$$

From (3.2) it follows that \(e^{b^*} = \left( \frac{r_2^2}{r_1^2}\right) ^{\frac{1}{r_1-r_2}}\). In the case \(b = b^{*}\) (i.e. \(b_r\le b^*\))

$$\begin{aligned} G'(0)&= \frac{r_1-r_2}{r_1e^{r_1b^*} -r_2e^{r_2b^*}} \nonumber \\&= \frac{ r_1-r_2}{ r_1 \left( \frac{r_2^2}{r_1^2}\right) ^{\frac{r_1}{r_1-r_2}}- r_2 \left( \frac{r_2^2}{r_1^2}\right) ^{\frac{r_2}{r_1-r_2}}}. \end{aligned}$$
(3.4)

Thus, \(G'(0) \le k\) if and only if (2.4) holds with reversed inequality in the case \(b = b^{*}\). Let us view \(G'(0)\) as a function of b which we denote by h, i.e. let

$$\begin{aligned} h(b):= \frac{r_1-r_2}{r_1e^{r_1b} -r_2e^{r_2b}}. \end{aligned}$$
(3.5)

From the definition of \(b^*\) it follows that the derivative of the denominator in (3.5), i.e. \(r_1^2e^{r_1b} -r_2^2e^{r_2b}\), is (strictly) positive when \(b>b^*\) and (strictly) negative when \(b<b^*\). It follows that h(b) is (strictly) decreasing in b for \(b>b^*\) and (strictly) increasing in b for \(b<b^*\). Hence, h(b) is maximal at \(b^*\). These facts imply that \(G'(0)\le k\) for all b. We remark that these facts and the function h will be used below. \(\square \)

Remark 3.3

Problem (3.1) was for a fairly general Itô diffusion solved in Paulsen (2003). In the case without a dividend payout barrier, i.e. with \(b_r=0\), the problem (3.1) is the well-known absorption problem first studied, for a fairly general Itô diffusion, in Shreve et al. (1984). In particular, in Shreve et al. (1984, Theorem 4.3) it was under appropriate assumptions—notably that the derivative of the drift function is dominated by the discount rate—shown that an upper barrier strategy \(\bar{D}^{b^*}\) is optimal, where the barrier \(b^*\) is determined by the additional boundary condition

$$\begin{aligned} f''(b^*)=0 . \end{aligned}$$
(3.6)

(If no such \(b^*\) exists, then no optimal strategy exists and the optimal value function is \(\lim _{b\rightarrow \infty }\mathbb {E}_x\left( \int _0^{\tau } e^{-\alpha t}d\bar{D}_t^b\right) \).) In particular, \(b^*\) in Theorem 3.1 is found using condition (3.6) for the value function (2.13).

3.2 Bankruptcy not allowed

Here we consider the problem (2.1) under the restriction that bankruptcy is not allowed. That is, we consider admissible strategies \((C,D) \in \mathcal A(x,b_r)\) for which

$$\begin{aligned} X_t \ge 0 ~ \text{ for } \text{ all } t \ge 0 \text{ a.s. } \end{aligned}$$

We denote the set of such strategies by \(\mathcal {A}^R(x,b_r)\). For this restricted problem it holds that \(\tau =\infty \) a.s. and the optimal value function (2.1) can be written as

$$\begin{aligned} \sup _{(C,D)\in \mathcal A^R(x,b_r)}\mathbb {E}_x\left( \limsup _{t\rightarrow \infty } \left( \int _0^te^{-\alpha s}dD_s - k\int _0^te^{-\alpha s}dC_s \right) \right) . \end{aligned}$$
(3.7)

Problem (3.7) has according to the authors’ knowledge not been considered before. The solution is given by:

Theorem 3.4

The double barrier strategy \((C^0,D^{b})\) with \(b=b_r\vee b^{**}\) is optimal in (3.7), where \(b^{**}>0\) is the unique positive solution to the equation

$$\begin{aligned}&r_1 e^{-r_2b^{**}} - r_2 e^{-r_1b^{**}} = k(r_1-r_2). \end{aligned}$$
(3.8)

Proof

The result can proved using arguments analogous to those in the proof of Theorem 4.1. The uniqueness of \(b^{**}\) is verified by noting that \(r_1e^{-r_2b} - r_2 e^{-r_1b}\) is strictly increasing in b; to see this use differentiation and (2.6). It is easy to see that \(b^{**}\) must be positive. A proof in the case \(b_r=0\) is found in Løkka and Zervos (2008, Sec. 4 and 5). \(\square \)

The value function corresponding to the strategy in Theorem 3.4 can, using the results of Sect. 2.1, be written as

$$\begin{aligned} H(x;b_r):={\left\{ \begin{array}{ll} \frac{1}{e^{r_1b}-e^{r_2b}}\left( \frac{1-ke^{r_2b}}{r_1}e^{r_1 x}-\frac{1-ke^{r_1b}}{r_2}e^{r_2x}\right) , &{}\quad 0 \le x \le b,\\ x-b+ \frac{1}{e^{r_1b}-e^{r_2b}}\left( \frac{1-ke^{r_2b}}{r_1}e^{r_1 b}-\frac{1-ke^{r_1b}}{r_2}e^{r_2b}\right) , &{}\quad x>b, ~ b=b_r\vee b^{**}. \end{array}\right. } \end{aligned}$$
(3.9)

We will typically write H(x) instead of \(H(x;b_r)\). Lemma 3.5 presents properties of the function H that are used when solving the main problem (2.1) in Sect. 4. The proof of Lemma 3.5 relies on the same type of arguments as the proof of Lemma 3.2 and is found in the “Appendix”.

Lemma 3.5

For H defined in (3.9) it holds that:

  1. (I)

    \(H'(x)>0\) for all \(x\ge 0\).

  2. (II)

    \(H(0)\ge 0\) is equivalent to

    $$\begin{aligned} r_1e^{r_1 b} - r_2e^{r_2 b} \le \frac{r_1-r_2}{k}. \end{aligned}$$
    (3.10)

    Moreover, \(H(0)\le 0\) is equivalent to (3.10) with reversed inequality.

  3. (III)

    Condition (2.4) is equivalent to \(b^{**}\le b^{*}\) which is equivalent to

    $$\begin{aligned} r_1e^{r_1b^{**}}-r_2e^{r_2b^{**}} \le \frac{r_1-r_2}{k}. \end{aligned}$$
    (3.11)

    Moreover, (2.4) with reversed inequality is equivalent to \(b^{**}\ge b^{*}\), which is equivalent to (3.11) with reversed inequality.

  4. (IV)

    Suppose \(b_r\le b^{**}\). Then, \(H(0)\ge 0\) is equivalent to (2.4), and \(H(0) \le 0\) is equivalent to (2.4) with reversed inequality.

  5. (V)

    Suppose (2.4) holds with reversed inequality. Then, for any \(b_r\), \(H(0)\le 0\).

  6. (VI)

    Suppose (2.4) holds. Then, \(H(0)\ge 0\) if and only if \(b_r\le {\hat{b}}\), where \({\hat{b}}\) is the unique solution, on the domain \([b^{**},\infty )\), to the equation

    $$\begin{aligned} r_1e^{r_1 {\hat{b}}} - r_2e^{r_2 {\hat{b}}} = \frac{r_1-r_2}{k}. \end{aligned}$$
    (3.12)

Remark 3.6

In the case \(b_r=0\) the problem (3.7) is the well-known reflection problem first studied, for a general Itô diffusion, in Shreve et al. (1984); see also Shreve et al. (1984, Sec. 5) where the problem is studied for a Wiener process with drift. In particular, in Shreve et al. (1984, Theorem 4.5) it was for the case \(b_r=0\) shown—under appropriate assumptions cf. Remark 3.3—that the double barrier strategy \((C^0,D^{b^{**}})\) is optimal, where the barrier \(b^{**}\) is given by the additional boundary condition

$$\begin{aligned} f''(b^{**})=0 . \end{aligned}$$
(3.13)

(If no such \(b^{**}\) exists, then no optimal strategy exists and the optimal value function is \(\lim _{b\rightarrow \infty }\mathbb {E}_x\left( \int _0^{\infty } e^{-\alpha t}dD_t^b -k\int _0^{\infty } e^{-\alpha t}dC^0_t \right) \).) In particular, \(b^{**}\) in Theorem 3.4 is found using condition (3.13) for the value function (2.15).

Remark 3.7

The equivalences in (III) in Lemma 3.5 were in the context of studying problem (2.1) without a dividend payout barrier, i.e. with \(b_r=0\), derived in Løkka and Zervos (2008).

4 Solution to the main problem

Since our model is Markovian it is reasonable to conjecture that the optimal strategy for problem (2.1) involves either that the owner always saves the insurance company from bankruptcy by injecting capital when the surplus process hits zero, or that the owner never does so. Indeed this is what we find in Theorem 4.1. The results in this section are illustrated in Sect. 4.1 and interpreted in Sect. 6.

Theorem 4.1

(Main result) Consider \(b^{*}\) defined in (3.2), \(b^{**}\) defined in (3.8) and \({\hat{b}}\) defined in (3.12). For problem (2.1) it holds that:

  1. (I)

    Suppose (2.4) holds.

    1. (I.a)

      If the dividend payout barrier satisfies \(b_r\le {\hat{b}}\), then the double barrier strategy \((C^0,D^b)\) with \(b = b_r\vee b^{**}\) is optimal. Moreover, the corresponding bankruptcy time, cf. (2.2), satisfies \(\tau =\infty \) a.s.

    2. (I.b)

      If \(b_r\ge {\hat{b}}\), then the upper barrier strategy \(\bar{D}^b\) with \(b = b_r\vee b^{*}\) is optimal. Moreover, the moments of the corresponding bankruptcy time are finite, i.e. \(\mathbb {E}_x\left( \tau ^n\right) <\infty \) for all \(x\ge 0\) and n.

  2. (II)

    Suppose (2.4) holds with reversed inequality. Then the upper barrier strategy \(\bar{D}^b\) with \(b = b_r\vee b^{*}\) is optimal for any given \(b_r\). Moreover, the corresponding bankruptcy time satisfies the same condition as in (I.b).

The interpretation is that \(b^{*}\) is the optimal dividend barrier in case capital injection is not allowed, \(b^{**}\) is the optimal dividend barrier in case capital injection is mandatory, and \({\hat{b}}\) is the regulation level which is such that if the dividend payout barrier satisfies \(b_r\le {\hat{b}}\), then it is optimal to inject capital when the insurance company needs it as long as (2.4) is satisfied.

Remark 4.2

A recursive formula for the moments of the bankruptcy times in (I.b) and (II) in Theorem 4.1 can be found in Wang and Yin (2008).

Using Theorem 4.1, (3.3) and (3.9) we immediately find:

Corollary 4.3

The optimal value function for problem (2.1) has the representation

$$\begin{aligned} V(x;b_r)&= \left\{ \begin{array}{l} H(x;b_r), \quad \text{ if } (2.4) \text{ holds } \text{ and } b_r \le {\hat{b}},\\ G(x;b_r), \quad \text{ if } (2.4) \text{ holds } \text{ with } \text{ reversed } \text{ inequality } \text{ or } b_r \ge {\hat{b}}, \end{array} \right. \\&= H(x;b_r) \vee G(x;b_r). \end{aligned}$$

Note that Corollary 4.3, (3.3) and (3.9) give an explicit expression for the optimal value function of problem (2.1).

The following properties of the solution of problem (2.1) are proved in the “Appendix”:

Corollary 4.4

Suppose (2.4) holds with strict inequality. If \(b_r<{\hat{b}}\), then \(V(0;b_r) = H(0;b_r) > G(0;b_r) = 0\). If \(b_r>{\hat{b}}\), then \(H(0;b_r) < V(0;b_r) = G(0;b_r) = 0\).

Remark 4.5

The interpretation of Corollary 4.4 is that in the case capital injection costs are low (in the sense that (2.4) holds with strict inequality) the following holds. If the dividend payout barrier satisfies \(b_r<{\hat{b}}\), then it is not optimal to allow bankruptcy. If the dividend payout barrier satisfies \(b_r>{\hat{b}}\), then it is not optimal to save the insurance company from bankruptcy.

Corollary 4.6

For any fixed \(x>0\) it holds that:

  1. (I)

    \(V(x;b_r)\) is decreasing in \(b_r\). In particular:

    1. (I.a)

      If (2.4) holds, then \(V(x;b_r)\) is independent of \(b_r\) for \(b_r\le b^{**}\) and strictly decreasing in \(b_r\) for \(b_r>b^{**}\).

    2. (I.b)

      If (2.4) holds with reversed inequality, then \(V(x;b_r)\) is independent of \(b_r\) for \(b_r\le b^{*}\) and strictly decreasing in \(b_r\) for \(b_r>b^{*}\).

  2. (II)

    \(\lim _{b_r\rightarrow \infty } V(x;b_r) = 0\).

Remark 4.7

It is easy to show that the results in Corollary 4.6 hold also in the case \(x=0\), with the modification that \(V(0;b_r)\) is only strictly decreasing in the case \(V(0;b_r)>0\), i.e. when (2.4) holds with strict inequality and \(b_r <{\hat{b}}\).

Proof of Theorem 4.1

We remark that this proof relies neither on Theorem 3.1 nor on Theorem 3.4.

Let us first deal with the results about the bankruptcy time \(\tau \). The result for (I.a) is trivial since X is reflecting at both b and 0 in this case. The result for (I.b) and (II) is contained in Wang and Yin (2008).

Now consider a function \(g \in \mathcal C^1([0,\infty )) \cap \mathcal C^2([0,b) \cup (b,\infty ))\) for some \(b>0\), an arbitrary strategy \((C,D)\in \mathcal A(x,b_r)\) and an arbitrary time \(t>0\). Similarly to e.g. Shreve et al. (1984, p. 60) and Løkka and Zervos (2008, p. 959) we note that for the right-continous process \((X_{(\tau \wedge t)+})_{t\ge 0}\) (cf. Remark 2.2) it holds, by the Itô-Tanaka formula, that

$$\begin{aligned}&e^{-\alpha (\tau \wedge t)}g(X_{(\tau \wedge t)+})\\&= g(x)+ \int _0^{\tau \wedge t} e^{-\alpha s}\left( \mu g'(X_s) +\frac{1}{2} \sigma ^2 g''(X_s)-\alpha g(X_s)\right) I_{\{X_s \ne b\}}ds \\&\quad + \int _0^{\tau \wedge t} e^{-\alpha s} \sigma g'(X_s) dW_s + \int _0^{\tau \wedge t} e^{-\alpha s} g'(X_{s})dC^c_s - \int _0^{\tau \wedge t} e^{-\alpha s} g'(X_{s}) dD^c_s\\&\quad + \sum _{0\le s\le \tau \wedge t} e^{-\alpha s} (g(X_s + \Delta C_s)- g(X_{s})) + \sum _{0\le s\le \tau \wedge t} e^{-\alpha s} (g(X_s - \Delta D_s)- g(X_{s})). \end{aligned}$$

The fundamental theorem of calculus gives

$$\begin{aligned} g(X_s + \Delta C_s)- g(X_{s})&= \int _0^{\Delta C_s}g'(X_s+z)dz,\\ g(X_s - \Delta D_s)- g(X_{s})&= - \int _0^{\Delta D_s}g'(X_s-z)dz. \end{aligned}$$

Now suppose g is either the value function of the upper barrier strategy \(\bar{D}^b\) with \(b = b_r\vee b^{*}\), given by G in (3.3), or the value function of the double barrier strategy \((C^0,D^b)\) with \(b = b_r\vee b^{**}\), given by H in (3.9)—the differentiability condition used above is directly verified in both cases. Then g satisfies (2.9) and (2.10) which implies that \(g'(x) = 1\) for \(x\ge b\) and \(g''(x)=0\) for \(x>b\).

These observations imply that

$$\begin{aligned} g(x)&= e^{-\alpha (\tau \wedge t)}g(X_{(\tau \wedge t)+}) - \int _0^{\tau \wedge t} e^{-\alpha s}\left( \mu -\alpha g(X_s)\right) I_{\{X_s > b\}}ds \\&\quad - \int _0^{\tau \wedge t} e^{-\alpha s} \sigma g'(X_s) dW_s - \int _0^{\tau \wedge t} e^{-\alpha s} g'(X_{s})dC^c_s + \int _0^{\tau \wedge t} e^{-\alpha s}g'(X_{s})dD^c_s\\&\quad - \sum _{0\le s\le \tau \wedge t} e^{-\alpha s} \int _0^{\Delta C_s}g'(X_s+z)dz + \sum _{0\le s\le \tau \wedge t} e^{-\alpha s} \int _0^{\Delta D_s}g'(X_s-z)dz. \end{aligned}$$

Lemma 7.2 gives \(\left( \mu -\alpha g(X_s)\right) I_{\{X_s > b\}}\le 0\) and therefore

$$\begin{aligned} g(x)&\ge e^{-\alpha (\tau \wedge t)}g(X_{(\tau \wedge t)+}) - \int _0^{\tau \wedge t} e^{-\alpha s} \sigma g'(X_s) dW_s\\&\quad +\int _0^{\tau \wedge t} e^{-\alpha s} g'(X_{s})dD^c_s + \sum _{0\le s\le \tau \wedge t} e^{-\alpha s} \int _0^{\Delta D_s}g'(X_s-z)dz\\&\quad -\int _0^{\tau \wedge t} e^{-\alpha s} g'(X_{s})dC^c_s - \sum _{0\le s\le \tau \wedge t} e^{-\alpha s} \int _0^{\Delta C_s}g'(X_s+z)dz. \end{aligned}$$

Hence,

$$\begin{aligned} g(x)&\ge \left( \int _0^{\tau \wedge t} e^{-\alpha s}dD_s- k \int _0^{\tau \wedge t} e^{-\alpha s}dC_s\right) \end{aligned}$$
(4.1)
$$\begin{aligned}&\quad + e^{-\alpha (\tau \wedge t)}g(X_{(\tau \wedge t)+}) - \int _0^{\tau \wedge t} e^{-\alpha s} \sigma g'(X_s) dW_s \end{aligned}$$
(4.2)
$$\begin{aligned}&\quad +\int _0^{\tau \wedge t} e^{-\alpha s} (g'(X_{s})-1)dD^c_s + \sum _{0\le s\le \tau \wedge t} e^{-\alpha s} \int _0^{\Delta D_s}(g'(X_s-z)-1)dz \end{aligned}$$
(4.3)
$$\begin{aligned}&\quad + \int _0^{\tau \wedge t} e^{-\alpha s} (k-g'(X_{s}))dC^c_s + \sum _{0\le s\le \tau \wedge t} e^{-\alpha s} \int _0^{\Delta C_s}(k-g'(X_s+z))dz. \end{aligned}$$
(4.4)

We conclude the proof by considering different cases. We rely on G in (3.3) solving (2.9) on [0, b), (2.10) and (2.11) with \(b=b_r\vee b^{*}\) and H in (3.9) solving (2.9) on [0, b), (2.10) and (2.14) with \(b=b_r\vee b^{**}\), cf. Sect. 2.1.

Case A: Consider the conditions of (I.a). Suppose g in inequality (4.1)–(4.4) is defined as H in (3.9). Suppose \(b_r\le b^{**}\) (i.e. \(b=b^{**}\)). Observe:

  • \(H'(x) = 1\) for \(x\ge b^{**}\) and \(H'(0)=k\). Since \(H'(x)>0\) for \(x \ge 0\) (Lemma 3.5) and \(H''(b^{**}) = 0\) (easily verified) it follows from Lemma 7.1 that \(H''(x)<0\) for \(x <b^{**}\). Hence, \(H'\) is non-increasing on \([0,b^{**}]\). It follows that \(1 \le H'(x) \le k\) for \(x\ge 0\). We conclude that the expressions (4.3) and (4.4) are non-negative.

  • Use Lemma 3.5 and \(b_r\le {\hat{b}}\) to find that \(H(0)\ge 0\) and \(H'(x)>0\) for \(x\ge 0\). Hence, \(H(x)\ge 0\) for \(x \ge 0\). We conclude that the first term in (4.2) is non-negative.

  • If we send t to infinity, then the second term in (4.2) converges a.s. to a random variable with zero expectation (use that \(H'(x)\) is a bounded function).

Thus, sending t to infinity (\(\limsup \)) in (4.1)–(4.4) and taking expectation give

$$\begin{aligned} H(x) \ge \mathbb {E}_x\left( \limsup _{t\rightarrow \infty }\left( \int _0^{\tau \wedge t} e^{-\alpha s} dD_s - k\int _0^{\tau \wedge t} e^{-\alpha s}dC_s \right) \right) . \end{aligned}$$

Since \((C,D) \in \mathcal A (x,b_r)\) was arbitrarily chosen it follows that (I.a) holds in the case \(b=b^{**}\) (recalling that H(x) is the value function attained by the strategy in (I.a)).

Now suppose \(b_r>b^{**}\) (i.e. \(b=b_r\)). Observe:

  • \(H'(x)=1\) for \(x\ge b_r\). The dividend payout condition (2.3) (see also Remark 2.3) therefore implies that the expressions in (4.3) vanish (either the derivatives are equal to one or there are no dividends).

  • \(H'(0)=k\), \(H'(x)>0\) and \(\lim _{x\nearrow b_r}H''(x) > 0\) (Lemma 7.2) for \(x\ge 0\). Using also Lemma 7.1 (and regularity of H) we thus have that: \(H'(0)=k\) and \(H'(b_r)=1\) with \(H'\) decreasing on an interval [0, c) and increasing on \((c,b_r]\) (with c determined by \(H''(c)=0\)). Hence, \(H'(x)\le k\) for \(x\ge 0\) and the terms in (4.4) are non-negative.

The terms in (4.2) are dealt with in the same way as above. Using the same limiting arguments as above we find that (I.a) holds also in the case \(b=b_r\).

Case B: Consider the conditions of (II). Suppose g in (4.1)–(4.4) is defined as G in (3.3). Suppose \(b_r\le b^{*}\). Observe:

  • \(G'(0)\le k\), \(G'(x)>0\) (Lemma 3.2) and \(G'(x) = 1\) for \(x \ge b^*\). From \(G''(b^{*}) = 0\) (easily verified) and Lemma 7.1 it follows that \(G''(x)<0\) for \(x <b^{*}\). Hence, \(G'\) is non-increasing on \([0,b^{*}]\). We conclude that \(1 \le G'(x) \le k\) for \(x\ge 0\).

  • \(G(0)=0\) (directly verified) and \(G(x)\ge 0\) (by the item above).

Using arguments analogous to those above we find that (II) holds in the case \(b=b^*\). Now suppose \(b_r>b^{*}\). Observe:

  • \(G'(x)=1\) for \(x\ge b_r\) and condition (2.3) imply that the expressions in (4.3) vanish (as above).

  • \(G'(0)\le k\), \(G'(x)>0\) and \(\lim _{x\nearrow b_r}G''(x) > 0\) (Lemma 7.2) for \(x\ge 0\). Using arguments similar to those in the second part of Case A we find that \(G'(x)\le k\).

  • As above we find that \(G(x)\ge 0\).

The usual arguments now imply that (II) holds also in the case \(b=b_r\).

Case C: We have left to prove (I.b). If \(G'(0)\le k\) holds also in this case, then the result follows by the exact same arguments as in Case B. Thus, it is enough to show that \(G'(0)\le k\) for \(b\ge {\hat{b}}\) when (2.4) holds. In (3.5) we defined the function h by

$$\begin{aligned} h(b) = \frac{r_1-r_2}{r_1e^{r_1b} -r_2e^{r_1b}} = G'(0). \end{aligned}$$

Hence, \(G'(0)= k\) when \(b={\hat{b}}\), by definition of \({\hat{b}}\) in (3.12). Thus, in order to prove that \(G'(0)\le k\) for any \(b\ge {\hat{b}}\) it is enough to show that h(b) is non-increasing in b for \(b\ge {\hat{b}}\). But h(b) is non-increasing exactly when \(b\ge b^*\), as we saw in the proof of Lemma 3.2. Hence, it is enough to prove that \({\hat{b}} \ge b^*\). The right side of (2.4) is equal to \(h(b^*)\), cf. (3.4). Use this, the definition of \({\hat{b}}\) in (3.12), and Lemma 3.5 to find \(k\le h(b^*), k = h({\hat{b}}), k\le h(b^{**}). \) But since h is maximal at \(b^*\), see the proof of Lemma 3.2, it follows that

$$\begin{aligned} k=h({\hat{b}}) \le h(b^{**})\le h(b^{*}). \end{aligned}$$
(4.5)

But since \({\hat{b}} \in [b^{**},\infty )\) by definition it follows that the only possibility is \({\hat{b}} \ge b^{*}\); to see this use \(b^{**}\le b^{*}\) (Lemma 3.5), (4.5), the fact that h(b) is non-decreasing when \(b\le b^*\) and non-increasing when \(b\ge b^*\). \(\square \)

4.1 Graphical illustrations

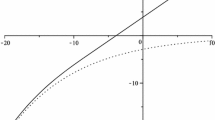
Recall that \(H(x;b_r)\) is the optimal value function without the possibility of bank-ruptcy, \(G(x;b_r)\) is the optimal value function without the possibility of capital injection and that the optimal value function when both bankruptcy and capital injection is allowed, i.e. \(V(x;b_r)\), is for any fixed \(b_r\) given by either \(H(x;b_r)\) or \(G(x;b_r)\) according to which is dominating the other, see Corollary 4.3. Figure 1 illustrates Theorem 4.1 and Corollary 4.3 by showing how increasing the dividend payout barrier \(b_r\) changes which of \(H(x;b_r)\) and \(G(x;b_r)\) is dominating. Figure 1 also illustrates Corollary 4.4. Figure 2 illustrates Corollary 4.6 by showing how \(V(x;b_r) = H(x;b_r) \vee G(x;b_r)\) (cf. Corollary 4.3) decreases in \(b_r\). Both figures illustrate that \(H(x;b_r)\) and \(G(x;b_r)\) coincide when \(b_r={\hat{b}}\), cf. Theorem 4.1. In Figs. 1 and 2 we use the parameters \(\mu =0.04\), \(\sigma ^2=0.15\), \(\alpha =0.05\) and \(k=1.01\) for which condition (2.4) holds with strict inequality, \(b^{**}\approx 0.17\), \(b^* \approx 0.75\) and \({\hat{b}} \approx 1.58\).

Fig. 1
figure 1

\(x\mapsto H(x;b_r)\) (solid) and \(x\mapsto G(x;b_r)\) (dashed) for different values of the dividend payout barrier \(b_r\). (Recall that the optimal value function is given by \(V(x;b_r) = H(x;b_r) \vee G(x;b_r))\)

Full size image
Fig. 2
figure 2

\(b_r\mapsto H(x;b_r)\) (solid) and \(b_r\mapsto G(x;b_r)\) (dashed) for different values of initial surplus x. The dashed vertical lines in each picture indicate \(b^{**}\), \(b^{*}\) and \({\hat{b}}\), in that order. (Recall that the optimal value function is given by \(V(x;b_r) = H(x;b_r) \vee G(x;b_r))\)

Full size image
Fig. 3
figure 3

\(b^*\) (solid), \(b^{**}\) (dashed), \(\hat{b}\) (dotted), and the right hand side of (2.4) (dash-dotted) as functions of \(c_\mu := \frac{\mu }{\sigma ^2}\). Here we fix \(c_{\alpha }:=\frac{\alpha }{\sigma ^2}=\frac{1}{3}\) and \(k=1.04\)

Full size image
Fig. 4
figure 4

\(b^*\) (solid), \(b^{**}\) (dashed), \({\hat{b}}\) (dotted), and the right hand side of (2.4) (dash-dotted) as functions of \(c_{\alpha }:=\frac{\alpha }{\sigma ^2}\). Here we fix \(c_\mu := \frac{\mu }{\sigma ^2}=\frac{4}{15}\) and \(k=1.04\)

Full size image

In Figs. 3 and 4 we consider the parametrization \(c_\mu := \frac{\mu }{\sigma ^2}\) and \(c_{\alpha }:=\frac{\alpha }{\sigma ^2}\) and illustrate how \(b^{*}\) (the optimal dividend barrier in case capital injection is not allowed), \(b^{**}\) (the optimal dividend barrier in case capital injection is mandatory), \({\hat{b}}\) (the regulation level which is such that if the dividend payout barrier satisfies \(b_r\le {\hat{b}}\), then it is optimal to inject capital when the insurance company needs it as long as (2.4) is satisfied), and the right hand side of (2.4) (the level for the proportional cost k which is such that if k is larger than this level then it can never be optimal to inject capital), depend on these parameters.

5 Adding the possibility of liquidation to the model

In this section we consider a version of the problem studied in the previous sections by supposing that the owner can at any time choose to liquidate the insurance company and receive a non-zero liquidation value. For ease of exposition we do not in this section consider the possibility of capital injection. In particular, we consider the combined singular stochastic control and stopping problem

$$\begin{aligned} \sup _{(D, \rho )\in \mathcal B(x,b_r)}\mathbb {E}_x\left( \int _0^{\rho \wedge \tau }e^{-\alpha t}dD_t + e^{-\alpha (\rho \wedge \tau )} L\left( X_{(\rho \wedge \tau )+}\right) \right) , \end{aligned}$$
(5.1)

where (i) \(L:[0,\infty )\rightarrow [0,\infty )\) is non-decreasing, concave and twice continuously differentiable with a bounded derivative and \(L(0)=0\), and (ii) \(\mathcal B(x,b_r)\) denotes the set of pairs \((D, \rho )\) where D is a non-decreasing LCRL \(\underline{\mathcal {F}}\)-adapted processes with \(D_0=0\) satisfying (2.3) for a dividend payout barrier \(b_r\ge 0\) and \(\rho \) is a stopping time with respect to \(\underline{\mathcal {F}}\).

The interpretation of problem (5.1) is that the owner of the insurance company not only chooses a dividend process D but also a stopping time \(\rho \) at which the insurance company will be liquidated—in case it has not already gone bankrupt—and the owner will receive a liquidation value \(L\left( X_{(\rho \wedge \tau )+}\right) \). The condition \(L(0)=0\) ensures that there is no liquidation value in case the insurance company goes bankrupt. Note that if \(L(x)<x\) for all x, then it can never be optimal to liquidate the insurance company since it would always be better to distribute the remaining surplus x and go bankrupt instead.

The main findings of this section are the two verification results Theorem 5.1 and Theorem 5.3 which say that the optimal strategy for problem (5.1) is, under certain conditions, a barrier strategy in the sense that it is optimal to (i) pay dividends in order to reflect the surplus process at an upper barrier, and (ii) liquidate the insurance company at a lower barrier; where these barriers are given by smooth fit conditions. These results are then used in Example 5.5.

Consider any two constants \(\bar{a}>\underline{a}>0\) and let the function U be given by

$$\begin{aligned} U(x;\underline{a},\bar{a}):={\left\{ \begin{array}{ll} L(x), &{}\quad 0 \le x \le \underline{a},\\ C_1 e^{r_1x} + C_2 e^{r_2x}, &{}\quad \underline{a} < x \le \bar{a},\\ x- \bar{a} + C_1 e^{r_1\bar{a}} + C_2 e^{r_2\bar{a}}, &{}\quad x > \bar{a}, \end{array}\right. } \end{aligned}$$
(5.2)

where \(C_1\) and \(C_2\) are defined so that \(x \mapsto U(x;\underline{a},\bar{a})\) is continous and continuously differentiable except at \(\underline{a}\), i.e.

$$\begin{aligned} C_1 := \left( L(\underline{a})-C_2e^{r_2\underline{a}} \right) e^{-r_1\underline{a}} ~ \text{ and }~ C_2 := \frac{1- r_1 L(\underline{a})e^{r_1(\bar{a}-\underline{a})} }{r_2 e^{r_2\bar{a}} -r_1 e^{r_1(\bar{a}-\underline{a}) + r_2\underline{a}}}. \end{aligned}$$
(5.3)

Theorem 5.1

Suppose there exists two constants \(0<{\underline{a}^*}<{\bar{a}^*}\) with \({\bar{a}^*}\ge b_r\) such that:

  1. (i)

    \(x \mapsto U(x;{\underline{a}^*},{\bar{a}^*})\), cf. (5.2), satisfies smooth fit in the sense that this function is continuously differentiable and twice continuously differentiable except at \({\underline{a}^*}\), i.e. such that \(U'({\underline{a}^*};{\underline{a}^*},{\bar{a}^*}) = L'({\underline{a}^*})\) and \(U''({\bar{a}^*;{\underline{a}^*},{\bar{a}^*}}) = 0.\)

  2. (ii)

    \(U(x;{\underline{a}^*},{\bar{a}^*})\ge L(x)\) for all \(x \ge 0\).

  3. (iii)

    \(\mu L'(x) +\frac{1}{2} \sigma ^2 L''(x)-\alpha L(x)\le 0\) for all \(0\le x \le {\underline{a}^*}\).

Then the optimal strategy in (5.1) is given by

$$\begin{aligned} D^{{\bar{a}^*}} ~ \text{ and }~ \rho ^{{\underline{a}^*}} := \inf \{t\ge 0: X_t < {\underline{a}^*} \}. \end{aligned}$$
(5.4)

Moreover, the optimal value function in (5.1) is given by \(x \mapsto U(x;{\underline{a}^*},{\bar{a}^*})\).

Remark 5.2

It can be directly verified that the definitions of \(C_1\) and \(C_2\) in (5.3) ensure that the function \(x \mapsto U(x;\underline{a},\bar{a})\) in (5.2) is continous and that its derivative is continous except at \({\underline{a}}\); and that smooth fit (cf. Theorem 5.1(i)) holds when \({\underline{a}} = {\underline{a}^*}\) and \({\bar{a}} = {\bar{a}^*}\) where \({\underline{a}^*}\) and \({\bar{a}^*}\) solve the non-linear equation system

$$\begin{aligned} {\left\{ \begin{array}{ll} r_1 C_1 e^{r_1{\underline{a}^*}} + r_2 C_2 e^{r_2{\underline{a}^*}} = L'({\underline{a}^*}) &{} \\ r_1^2 C_1 e^{r_1{\bar{a}^*}} + r_2^2C_2 e^{r_2{\bar{a}^*}} = 0. &{} \end{array}\right. } \end{aligned}$$

The interpretation of the condition \({\bar{a}^*}\ge b_r\) in Theorem 5.1 is that the dividend payout barrier \(b_r\) is not binding. We now consider a binding dividend payout barrier.

Theorem 5.3

Suppose \(b_r > {\bar{a}^*}\) and that there exists a constant \(0<\underline{a}_{b_r}<b_r\) such that:

  1. (i)

    \(x \mapsto U(x;\underline{a}_{b_r},b_r)\) satisfies smooth fit in the sense that this function is continuously differentiable, i.e. \(U'(\underline{a}_{b_r};\underline{a}_{b_r},b_r) = L'(\underline{a}_{b_r})\). Also, \(\lim _{ x \nearrow b_r}U''(x;\underline{a}_{b_r},b_r)\) \(\ge 0\).

  2. (ii)

    \(U(x;\underline{a}_{b_r},b_r)\ge L(x)\) for all \(x \ge 0\).

  3. (iii)

    \(\mu L'(x) +\frac{1}{2} \sigma ^2 L''(x)-\alpha L(x)\le 0\) for all \(0\le x \le \underline{a}_{b_r}\).

Then the optimal strategy in (5.1) is given by

$$\begin{aligned} D^{b_r} ~ \text{ and }~ \rho ^{\underline{a}_{b_r}} := \inf \{t\ge 0: X_t < \underline{a}_{b_r} \}. \end{aligned}$$

Moreover, the optimal value function in (5.1) is given by \(x \mapsto U(x;\underline{a}_{b_r},b_r)\).

Remark 5.4

The problem in (5.1) is a combined optimal stopping and singular stochastic control problem. We remark that it is likely possible to prove more general verification results than Theorems 5.1 and 5.3 and to further investigate this problem from different perspectives. However, a more complete investigation of problem (5.1) is outside the scope of the present paper.

Proof of Theorem 5.1

Using the same line of arguments as in Sect. 2 we find that if we the use the strategy in (5.4) in the expected value in the right hand side of (5.1), then this expected value is equal to \(U(x;{\underline{a}^*},{\bar{a}^*})\), cf. (5.2), for each \(x\ge 0\). (Note that using also (5.2) and (2.6) it is easy to see that \(C_1>0\).) Hence, we now only have to prove that \(U(x;{\underline{a}^*},{\bar{a}^*})\) dominates the expected value in the right hand side of (5.1) for any admissible strategy \((D,\rho )\). In the rest of this the proof we write U(x) instead of \(U(x;{\underline{a}^*},{\bar{a}^*}\)). Observe:

  • \(C_1 e^{r_1x} + C_2 e^{r_2x}\) solves the ODE (2.9).

  • For \(x \ge {\bar{a}^*}\), it holds that

    $$\begin{aligned} \mu - \alpha U(x) = \mu - \alpha (x-{\bar{a}^*}+U({\bar{a}^*}))\le \mu - \alpha U({\bar{a}^*}) = 0. \end{aligned}$$

    To see that the last equality holds observe that \(\mu U'(x) +\frac{1}{2} \sigma ^2 U''(x)-\alpha U(x)=0, {\underline{a}^*}<x<{\bar{a}^*}\), send \(x\nearrow {\bar{a}^*}\) and use the smooth fit condition (i). The first equality follows directly from (5.2).

From these observations, (5.2) and (iii) it follows that

$$\begin{aligned} \mu U'(x) +\frac{1}{2} \sigma ^2 U''(x)-\alpha U(x)= & {} {\left\{ \begin{array}{ll} \mu L'(x) +\frac{1}{2} \sigma ^2 L''(x)-\alpha L(x), &{}\quad 0<x< {\underline{a}^*}\\ 0, &{}\quad {\underline{a}^*} < x \le {\bar{a}^*}\\ \mu - \alpha U(x), &{}\quad x > {\bar{a}^*} \end{array}\right. }\nonumber \\\le & {} 0.~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ \end{aligned}$$
(5.5)

Using (5.5) and arguments similar to those in the proof of Theorem 4.1 we now find that for any admissible strategy \((D,\rho )\) and \(t>0\) it holds that

$$\begin{aligned} U(x)&\ge \int _0^{\rho \wedge \tau \wedge t} e^{-\alpha s}dD_s + e^{-\alpha (\rho \wedge \tau \wedge t)}U(X_{(\rho \wedge \tau \wedge t)+}) \end{aligned}$$
(5.6)
$$\begin{aligned}&\quad - \int _0^{\rho \wedge \tau \wedge t} e^{-\alpha s} \sigma U'(X_s) dW_s \end{aligned}$$
(5.7)
$$\begin{aligned}&\quad +\int _0^{\rho \wedge \tau \wedge t} e^{-\alpha s}\left( U'(X_{s})-1\right) dD^c_s \nonumber \\&\quad + \sum _{0\le s\le \rho \wedge \tau \wedge t} e^{-\alpha s} \int _0^{\Delta D_s}\left( U'(X_s-z)-1\right) dz. \end{aligned}$$
(5.8)

Now observe:

  • Since \(C_1>0\) (see the beginning of the proof) it follows from \(U''({\bar{a}^*})= r_1^2 C_1 e^{r_1{\bar{a}^*}} + r_2^2C_2 e^{r_2{\bar{a}^*}} =0\) (cf. (i) and Remark 5.2) that \(C_2<0\), which implies, see also (2.6), that \(r_1^2 C_1 e^{r_1x} + r_2^2C_2 e^{r_2x}\) is a strictly increasing function. Hence, \(U''(x)<0,{\underline{a}^*}<x<{\bar{a}^*}\), which implies that \(U'(x)\) is non-increasing on \(({\underline{a}^*},{\bar{a}^*})\). Moreover, since \(U(x)=L(x), 0\le x \le {\underline{a}^*}\) and L is concave it also holds that \(U'(x)\) is non-increasing on \([0,{\underline{a}^*})\). Hence, since \(U'(x)\) is continuous, it follows that \(U'(x)\) is non-increasing on \([0,{\bar{a}^*})\). Using also that \(U'(x)=1, x\ge {\bar{a}^*}\), we thus conclude that

    $$\begin{aligned}U'(x)-1\ge 0, ~ \text{ for } \text{ all } x>0.\end{aligned}$$

  • Using that L(x) has a bounded derivative it is easy to see that also U(x) has a bounded derivative. Hence, using arguments similar to those in the proof of Theorem 4.1, we find that the Itô integral in (5.7) converges a.s. to a random variable with zero expectation as \(t\rightarrow \infty \).

From the items above it follows that sending \(t\rightarrow \infty \) in the expression (5.6)–(5.8) and taking expectation yield

$$\begin{aligned} U(x) \ge \mathbb {E}_x\left( \int _0^{\rho \wedge \tau } e^{-\alpha t} dD_t + e^{-\alpha \rho \wedge \tau }U(X_{(\rho \wedge \tau )+}) \right) , \end{aligned}$$

which, using also (ii), concludes the proof. \(\square \)

Proof of Theorem 5.3

In this proof we write U(x) instead of \(U(x;\underline{a}_{b_r},b_r)\). A proof of the present result can easily be found by making a few alterations to the proof of Theorem 5.1 according to the following:

  • A statement analogous to that of (5.6)–(5.8) holds also in the present case. To arrive at this version of (5.6)–(5.8) use arguments analogous to those in the proof of Theorem 5.1; in this case the analogue of (5.5) is found for \(\underline{a}_{b_r}\) instead of \(\underline{a}^*\) and \(b_r\) instead of \(\bar{a}^*\) and relying on \(\mu -\alpha U(b_r)\le 0\) (to see that this inequality holds use arguments similar to those in the proof of Theorem 5.1 but relying on the condition \(\lim _{ x \nearrow b_r}U''(x)\ge 0\), see Theorem 5.3(i)).

  • Similarly to the proof of Theorem 4.1 note that \(U'(x)=1,x\ge b_r\) and that from this and the condition (2.3) it follows that the last two terms in present version of (5.6)–(5.8) vanish (since (2.3) implies that for any admissible strategy \((D,\rho )\) it holds that either there are no dividends or \(X_t\ge b_r\)). \(\square \)

Example 5.5

Suppose the liquidation value is given by \(L(x)=c\log (x+1)\) and that the parameters of the model are \(c=1.8\), \(\mu =0.08\), \(\sigma ^2=0.4\) and \(\alpha =0.03\). Let us consider the dividend payout barriers \(b_r=0\) and \(b_r=4.5\). In the unregulated case \(b_r=0\) the conditions (i)–(iii) in Theorem 5.1 are satisfied for \({\underline{a}^*} \approx 0.2762\) and \({\bar{a}^*} \approx 2.2566\); meaning that it is optimal to pay dividends in order to reflect the surplus process at the upper barrier \({\bar{a}^*} \approx 2.2566\) and liquidate the insurance company at a lower barrier \({\underline{a}^*} \approx 0.2762\). In the case \(b_r=4.5\) conditions (i)–(iii) in Theorem 5.3 are satisfied for \({a_{b_r}} \approx 1.5434\); meaning that it is optimal to pay dividends in order to reflect the surplus process at the dividend payout barrier \(b_r\) and liquidate the insurance company at a lower barrier \({a_{b_r}} \approx 1.5434\). We conclude that the introduction of a binding dividend payout barrier (\(b_r>\bar{a}^*\)) implies a higher liquidation barrier (\({a_{b_r}} >\underline{a}^*\)), i.e. earlier liquidation, in this example. The corresponding value functions are depicted in Fig. 5.

Fig. 5
figure 5

The liquidation value (dotted) and optimal value function in the case without regulations i.e. with \(b_r=0\) (upper solid) and in the case \(b_r=4.5\) (lower solid) from Example 5.5. The vertical lines indicate \({\underline{a}^*}\) and \(a_{b_r}\) (the liquidation barriers), and \({\bar{a}^*}\) and \(b_r\) (the dividend barriers), in that order

Full size image

6 Conclusions

The main interpretation of the results in this paper, in particular of items (I.a) and (I.b) in Theorem 4.1, see also Figs. 1 and 2, is that if the proportional cost of injecting capital k is low, i.e. if (2.4) holds, then it is optimal to use a double barrier financing strategy and never allow the insurance company to go bankrupt as long as the dividend payout barrier \(b_r\) is lower than the level \({\hat{b}}\), i.e. the optimal value function is given by \(V(x;b_r)=H(x;b_r)\); see Corollary 4.3 and (3.9). However, if the dividend payout barrier \(b_r\) is set higher than \({\hat{b}}\), then the optimal behavior switches to an upper barrier strategy that lets the insurance company go bankrupt the first time the surplus reaches zero, i.e. the optimal value function is given by \(V(x;b_r)=G(x;b_r)\); see Corollary 4.3 and (3.3). Moreover, the interpretation of Corollary 4.6, see also Fig. 2, is that an increase in the dividend payout barrier decreases the optimal value function (i.e. the value of the insurance company), with the corresponding limit being zero.

The main economic conclusion of this paper is that restrictive regulations may have a negative effect on the longevity of the regulated company. In particular, if a profitable insurance company (corresponding to \(\mu >0\)) has access to a well-functioning financial market (corresponding to the proportional costs for capital injection k satisfying (2.4)), then its owners will inject capital when needed in case the market is unregulated or at least not too heavily regulated (\(b_r\le {\hat{b}}\)). However, if the regulation is sufficiently heavy (\(b_r>{\hat{b}}\)), then the owners of the same insurance company will change their behavior; specifically, they will never inject capital and instead let the insurance company go bankrupt in the case of financial distress, i.e. in the case of zero surplus.

In Sect. 5 we study a version of our problem under the assumption that the owner can at any time liquidate the insurance company and thereby receive a liquidation value depending on the current surplus, but not inject capital. The main results are Theorems 5.1 and 5.3, which say that, under certain conditions, the optimal strategy is to pay dividends so that the surplus is reflected at an upper barrier and liquidate the insurance company at a lower barrier.