New heuristic algorithms for the Dubins traveling salesman problem

Abstract

The problem of finding a shortest curvature-constrained closed path through a set of targets in the plane is known as Dubins traveling salesman problem (DTSP). Applications of the DTSP include motion planning for kinematically constrained mobile robots and unmanned fixed-wing aerial vehicles. The difficulty of the DTSP is to simultaneously find an order of the targets and suitable headings (orientation angles) of the vehicle when passing the targets. Since the DTSP is known to be NP-hard there is a need for heuristic algorithms providing good quality solutions in reasonable time. Inspired by standard methods for the TSP we present a collection of such heuristics adapted to the DTSP. The algorithms are based on a technique that optimizes the headings of the targets of an open or closed subtour with given order. This is done by discretizing the headings, constructing an auxiliary network and computing a shortest path in the network. The first algorithm for the DTSP uses the order of the targets obtained from the solution of the Euclidean TSP. A second class of algorithms extends an open subtour by successively adding a new target and closes the tour if all targets have been added. A third class of algorithms starts with a closed subtour consisting of few targets and successively inserts a new target into the tour. The individual algorithms differ by the number of headings to be optimized in each iteration. Extensive simulation results show that the proposed methods are competitive with state-of-the-art methods for the DTSP concerning performance and superior concerning running time, which makes them applicable also to large-scale scenarios.

1 Introduction

The Traveling Salesman Problem (TSP) is one of the most intensely studied problems in combinatorial optimization. Given a set of targets, the task is to determine a shortest tour that visits each target precisely once and returns to the start. If the distance between any two targets is equal to the Euclidean distance, the problem is called the Euclidean Traveling Salesman Problem (ETSP). The Asymmetric Traveling Salesman Problem (ATSP) is a problem where the distance between two targets is not symmetric but depends on the direction of the traversal. Further variations of the TSP include the Traveling Salesman Problem with Neighborhoods (TSPN) where each target of the tour is allowed to move in a given region, the Bottleneck Traveling Salesman Problem (BTSP) where the largest distance between two targets in the tour should be minimized, and others. For more details see e.g. the reviews of Lawler et al. (1985), Laporte (1992) and Gutin and Punnen (2007).

The route planning problems listed above are aimed at finding best possible tours without taking into account the characteristics of the vehicle. However, when working with real-world vehicles, one has to consider kinematic constraints such as the minimum turning radius. Vehicles with motion constraints imposed by the steering mechanism satisfy a non-holonomic constraint. Such vehicles are not able to follow paths obtained from solutions of the classical TSP problems. Car-like mobile robots or fixed-wing aerial vehicles that move forward at a constant speed and turn with upper bounded curvature can be modeled as a Dubins vehicle (see e.g. Tang and Özgüner 2005; Otto et al. 2018). The traveling salesman problem for a Dubins vehicle is usually called Dubins Traveling Salesman Problem (DTSP) or Curvature-constrained TSP (see LaValle 2006).

The DTSP has attracted considerable attention due to many civil and military applications. A typical setup is monitoring a collection of spatially distributed targets by an unmanned aerial vehicle (UAV). This might concern traffic control over specific locations, intelligence gathering and reconnaissance of suspicious targets for anti-terrorism operations, security missions and monitoring of critical infrastructure and other point of interests, support of combat missions by intelligence, surveillance and reconnaissance (ISR) operations, battle damage assessment (confirming a target and verifying its destruction), and others. For further applications see e.g. Epstein et al. (2014) and Otto et al. (2018).

It is well known (see Dubins 1957) that a shortest path between two points in the plane with prescribed initial and terminal tangents and a constraint on the curvature consists of a concatenation of straight lines and circle segments with maximal curvature. More precisely, each path is of the form CSC or CCC where C stands for a concave or convex circle segment with maximal curvature and S for a line segment. The solutions are commonly called Dubins paths. Alternative proofs have been obtained by Reeds and Shepp (1990) using advanced calculus, and by Boissonnat et al. (1994) from the standpoint of optimal control using Pontryagin’s maximum principle. The original idea of Dubins has been refined by Shkel and Lumelsky (2001) in order to speed up the computation of the paths.

The particular challenge associated with the DTSP is not only to find an optimal order of the targets but also suitable headings (orientation angles) of the vehicle when passing the targets. Since the target order is discrete but the heading angles are continuous, we obtain an optimization problem with both discrete and continuous decision variables. Just like the TSP and its variations mentioned above, the DTSP turns out to be NP-hard (see Le Ny et al. 2012). Therefore, unless P = NP, there are no efficient algorithms to solve any of these problems to optimality. Hence there is a need for methods providing approximate solutions in reasonable time.

Numerous heuristic methods have been developed for the DTSP. One popular approach is to use the order obtained from the corresponding ETSP and determine suitable headings of the targets. Representatives of such methods include the Alternating Algorithm of Savla et al. (2008) that replaces the even-numbered edges of an ETSP tour by a Dubins path. The algorithms of Rathinam et al. (2007) and Ma and Castanon (2006) are look-ahead algorithms that consider a short sequence of targets in each iteration. While the former restricts to two targets, the second algorithm searches for the minimal path through three targets at a time. Another method proposed by Macharet and Campos (2014) assigns orientations to each target, taking into account the turning radius and the distance between targets.

Methods that do not apply the ETSP order include the algorithms of Tang and Özgüner (2005) and Le Ny et al. (2007). The first determines an order by geometric reasoning and computes a path through the targets using an approximated gradient method. The second algorithm, called Nearest Neighbor Heuristic, adds one target to the order in each step and fixes its heading, namely the target closest to the last added configuration according to the Dubins metric. A further algorithm proposed by Medeiros and Urrutia (2010) adopts an angular-metric traveling salesman problem to minimize the sum of direction changes in determining the visiting order.

A well known technique for finding a Dubins path through an ordered set of targets, in the following referred to as the Dubins Shortest Path Problem (DSPP), is to discretize the headings of the targets, that is, for each target, to consider h candidate headings that partition the interval $[0, 2\pi ]$ uniformly into h subintervals. The idea has been used in the context of motion planning of robots by several authors including Jacobs and Canny (1992), Edison and Shima (2011), Cons et al. (2014) and others. Alternative approaches for the DSPP are due to Goac et al. (2013), Lee et al. (2000), Rathinam and Khargonekar (2016) and Manyam et al. (2017).

Discretization is also the basis of several approaches for the DTSP. Le Ny et al. (2012) propose a method that chooses a set of possible headings at each target and transforms the problem into a larger asymmetric TSP. Epstein et al. (2014) discretize the problem and formulate it as an integer optimization problem. The authors solve problems with up to 30 targets, however requiring several hours of running time on a standard desktop computer. Isaiah and Shima (2015) develop a k-step look-ahead algorithm and solve small-size problems with up to nine targets. Additionally, they propose a local improvement algorithm similar to the classic 2-opt algorithm for the TSP. Cohen et al. (2016) continue this work and present discretization-based look-ahead algorithms with different discretization levels and lengths of the look-ahead horizon. They solve problems with up to 30 targets requiring not more than few tens of minutes, even for high discretization levels.

Another line of research applies global search metaheuristics to both the DSPP and DTSP. This includes the genetic algorithms of Yu and Hung (2012) and Hansen and La Cour-Harbo (2016). The former presents a coupled strategy where both headings and sequence of the targets are determined concurrently. The latter extends the algorithm by allowing Dubins curves with varying turning radii. This is motivated by the fact that lowering the forward speed of an aircraft reduces the turning radius. Macharet et al. (2011) use a continuous GRASP technique consisting of a construction and local improvement phase. Kenefic (2008) applies particle swarm optimization to solve the DSPP. The method starts with a solution of the Alternating Algorithm and optimizes the headings at each target to smooth the entire path such that there are as few large or complete turns as possible.

In this paper we present a collection of new heuristic algorithms for the DTSP and evaluate their performance empirically. The algorithms are inspired by standard methods for the TSP and are based on several variants of the DSPP which are solved by discretizing the headings, constructing an auxiliary network and finding a shortest path in the network. The proposed heuristics are suitable for solving large instances of the DTSP with thousand or more targets, while keeping computation times low. Tested on a large variety of random scenarios with different turning radii of the Dubins vehicle, the methods show a significant performance improvement over standard methods known from the literature. Moreover, the methods appear competitive with the state-of-the-art algorithm of Le Ny et al. (2012), however with a much lower computation time.

The remainder of the paper is structured as follows. In Sect. 2 we outline the network-based approach to solve the DSPP and numerically analyze the performance with respect to different discretization levels of the headings. Section 3 presents algorithms for the DTSP based on the target order of the Euclidean TSP. A class of algorithms that extends an open subtour by successively adding a new target is introduced in Sect. 4. In Sect. 5 we propose a further class of algorithms that starts with a closed subtour consisting of few targets and successively inserts a new target into the tour. Section 6 discusses the trade-off between quality of solutions and running time and attempts a final assessment of the different methods. We conclude in Sect. 7 with final remarks.

2 Optimization of headings

In this section we address several variants of the DSPP. The solution method is interesting in its own right, and will serve as the basis for the algorithms of the DTSP. The following four problems are investigated. Given a specified order $T_1,\ldots ,T_n$ of the targets find a shortest possible:

• (I) open Dubins tour with predefined headings in $T_1$ and $T_n$

• (II) open Dubins tour without predefined headings in $T_1$ and $T_n$

• (III) open Dubins tour with predefined heading in $T_1$ and without predefined heading in $T_n$

• (IV) closed Dubins tour.

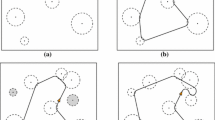
Figure 1 shows examples of such tours for a set of five targets with turning radius $r=1$. The headings of the first and last target in the open tour of subfigure (a) are predefined as $180^{{\circ }}$ and $90^{{\circ }}$, respectively. All other headings are free and have been determined as to minimize tour length. The open tour in subfigure (b) has been generated without predefined headings, i.e. all headings are optimized. Subfigure (c) shows a closed tour where all headings are optimized.

Fig. 1

Open and closed Dubins tours with optimized headings

In the following we present a technique that optimizes the headings of the targets in a tour with a given order. The method is based on finding a shortest path in an auxiliary network. The network is constructed by discretizing the headings of the targets. Each target without predefined heading is associated with m vertices where m denotes the number of different headings in the discretization. Each vertex represents the target with a special heading.

The network to solve problem (I) consists of a vertex s representing the first target $T_1$ of the tour with the predefined heading and a vertex t representing the last target $T_n$, again with predefined heading. Every other target $T_2,\ldots ,T_{n-1}$ is represented by m vertices forming a layer of the network. All vertices of consecutive layers are connected by directed edges. The weight of an edge is equal to the Dubins distance between the targets with the associated headings. Vertex s is connected to all vertices of the first layer and all vertices of the last layer are connected to t. The idea is sketched in Fig. 2a. Obviously, for the given discretization, a shortest path in the network from s to t provides a tour with optimal headings of the targets $T_2,\ldots ,T_{n-1}$.

The network for problem (II) consists of n layers for the targets $T_1,\ldots ,T_n$ and two auxiliary vertices s and t, see Fig. 2b. All edges from s to the first layer get weight 0 as well as all edges from the last layer to vertex t. A shortest path from s to t provides a shortest tour where the headings of all targets are optimized. Problem (III) is addressed by defining $n-1$ layers for $T_2,\ldots ,T_n$ along with a vertex s representing the first target $T_1$ with predefined heading and an auxiliary vertex t with incoming edges of weight 0, see Fig. 2c. Now a shortest path from s to t corresponds to a shortest tour with optimal headings for $T_2,\ldots ,T_n$.

The network for problem (IV) consists of $n+1$ layers for $T_1,\ldots ,T_n$ and $T_1$ as shown in Fig. 2d. The vertices of the first layer are denoted by $s_1,\ldots ,s_m$, the vertices of the last layer by $t_1,\ldots ,t_m$. Hence $s_i$ and $t_i$ represent target $T_1$ with the same heading. The shortest path from $s_i$ to $t_i$ corresponds to a closed Dubins tour with predefined heading in $T_1$. The shortest tour is obtained by calculating all m shortest paths from $s_i$ to $t_i$, $i=1,2,\ldots ,m$ and selecting the shortest one. Shortest path calculations are performed using the $A^*$-algorithm (see Hart et al. 1968).

Fig. 2

Shortest paths in auxiliary networks

It should be noted that the lengths of the Dubins tours are not continuous with respect to the discretization level of the headings. Even small changes of the discretization may completely change the course of the tour and significantly increase or decrease the tour length. For that reason it is advisable to choose as fine a discretization as possible. Figure 3 shows an example where different discretization levels provide completely different Dubins tours. The turning radius of the Dubins vehicle is $r=0.5$. The length of the tour decreases when the stepsize is reduced from $10^{\circ }$ to $5^{\circ }$, however it increases when the stepsize is further reduced to $2^{\circ }$.

Fig. 3

Dubins tours with different discretization levels of headings

Table 1 Normalized tour lengths depending on discretization level

All algorithms presented in this paper have been implemented in Matlab version R2018a, on a standard PC running Windows 10 with 3.5 GHz CPU and 8 GB RAM. In order to assess the performance of the above methods, the tour length is considered as a function of the discretization level of the headings. A wide range of test cases has been generated where the targets are located randomly according to a uniform distribution in an area of size $[-2.5, 2.5] \times [-2.5, 2.5]$. We compute open Dubins tours through a number $n \in \{10, 50, 100 \}$ of targets arranged in random order with different turning radii $r \in \{0.1, 0.5, 1.0\}$. The lengths of all tours are normalized (divided) by the length of the Euclidean tour consisting of straight-line connections (i.e. the length of the normalized straight-line tour is equal to 1). Table 1 shows the average of 100 random instances for each combination of n and r.

It can be seen that the results stabilize very soon if the turning radius is small. In this case, independent of the number of targets, a relatively rough discretization of $10^{\circ }$ appears sufficient. A further reduction of the stepsize offers only minor improvements. With increasing turning radius it is advisable to select a finer discretization.

The running time of the algorithm depending on the discretization level is shown in Fig. 4 using a logarithmic scale of the time axis. For example, computing a tour consisting of 10 targets requires about 1 s for a discretization of $5^{\circ }$ and 25 s for a fine discretization of $1^{\circ }$. Tours consisting of 100 targets are computed within approximately 10 s for stepsize $5^{\circ }$. For a stepsize of $1^{\circ }$ the running time grows to almost five minutes. The strong increase is due to the fact that, in the last case, a huge network consisting of 100 layers with 360 vertices each has to be constructed, resulting in a total of 36,000 vertices. Calculating the Dubins distances between all pairs of vertices of consecutive layers is time-consuming, whereas finding a shortest path with the $A^*$-algorithm is very fast.

Fig. 4

Average computation time for open Dubins tour

3 Algorithms based on solutions of the ETSP

In this section we compare several algorithms that are based on an order of the targets obtained from an optimal solution of the Euclidean Traveling Salesman Problem (ETSP). The algorithms fix the headings of the targets according to different strategies.

The Randomized Headings Algorithm assigns the headings purely at random (see Le Ny et al. 2007). The Alternating Algorithm (see Savla et al. 2005) retains all odd-numbered edges of the solution of the ETSP (i.e. the subpath is a straight line) as well as the corresponding headings. The even-numbered edges are replaced by Dubins paths. The Optimized Headings Algorithm uses the technique for subproblem (IV) introduced in the previous section. As a benchmark and lower bound we use the solution of the ETSP.

Fig. 5

Results of algorithms based on optimal solution of the ETSP

The scenario in Fig. 5 with 20 targets and turning radius 0.5 shows the strong impact of the headings on the course and the length of the Dubins tour. The Optimized Headings Algorithm has been applied with a discretization of stepsize $5^{{\circ }}$. Clearly, if the headings of the Alternating Algorithm are included in the discretization of the headings of the Optimized Headings Algorithm, then the latter algorithm will always provide a solution that is at least as good.

The impact of the turning radius on the course of the tour is shown in an example in Fig. 6. For a small turning radius, the order obtained from the ETSP is in most cases appropriate to produce a good solution of the DTSP since the kinematic constraints are less relevant. However, this is not necessarily the case if the radius increases. For a vehicle with large turning radius we get solutions with many loops which may be improved by modifying the order of the targets.

The performance of the algorithms has been tested on scenarios with n targets, again located uniformly at random in an area of size $[-2.5, 2.5] \times [-2.5, 2.5]$, where $n=10,20,\ldots ,100$, and turning radius $r \in \{0.1,0.5,1.0\}$. The diagrams in Fig. 7 show the average of 50 instances, normalized with respect to the length of the ETSP. The ETSP has been solved using Helsgaun’s implementation of the Lin–Kernighan heuristic (see Helsgaun 2000). The Optimized Headings Algorithm uses a $10^{\circ }$ discretization for turning radius $0.1^{\circ }$ and $5^{\circ }$ for turning radius 0.5 and 1.0.

It is evident that the Optimized Headings Algorithm clearly outperforms the other methods. For turning radius 0.1 and 0.5, the improvement of the tour length compared to the Alternating Algorithm is about 25% for 10 targets. The percentage drops slightly with increasing number of targets to about 20% for 100 targets. For turning radius 1.0, we get more than 30% improvement for 10 targets and 10% for 100 targets. Not surprisingly, the Randomized Headings Algorithm is not competitive.

Fig. 6

Tours obtained by Optimized Headings Algorithm

The proposed algorithm provides a significant improvement of the tour length for small turning radii. The reason for this is that the algorithm allows a wide range of possible headings and the vehicle is agile enough to prevent it from performing big loops. On the other side, the gap to the Alternating Algorithm gets smaller if the radius and the number of targets increases. This may be explained as follows. If the targets are close together compared to the turning radius, then only few targets can be passed in a row with small maneuvers. Very often, the vehicle will have to make a wide turn to get to the next target. The length of such a turn by far exceeds the length of the direct connection. One half of the solution of the Alternating Algorithm are straight-line connections, the other connections are mostly wide turns. In order to significantly improve such a solution, one should avoid the turns which is only possible to a limited extend due to the restricted maneuverability of the vehicle.

Fig. 7

Computational results for ETSP-based algorithms

4 Extension algorithms

Inspired by the nearest neighbor method for the TSP, see e.g. Lawler et al. (1985), the Nearest Neighbor Heuristic for the DTSP has been introduced by Le Ny et al. (2012). The method starts with an arbitrary target and defines its heading arbitrarily. Then, at each step, the target is determined which is not yet on the path but is closest to the last added target (with already fixed heading) according to the Dubins metric. The authors use an idea of Savla et al. (2005) that computes the Dubins distance and path between an initial target with fixed heading and a final target with free heading. The closest target is added to the path with the associated optimal arrival heading. In a final step, when all targets have been added to the path, the tour is completed by a Dubins path connecting the last and the initial target.

The Nearest Neighbor Heuristic optimizes the heading of the newly added target only, whereas the headings of all previously inserted targets remain fixed. In contrast, the following algorithm optimizes the headings of all included targets.

Algorithm:Greedy-extend

• 1. Start with an arbitrary target $T_1$.

• 2. For $p = 1$ to $n-1$ do

  Choose the next target $T_{p+1}$ in such a way that the open

  Dubins tour through $T_1 ,\ldots , T_p ,T_{p+1}$ is as short as possible.

• 3. Find a shortest possible closed Dubins tour through $T_1,T_2,\ldots ,T_n$.

  Let $h_1,\ldots ,h_n$ denote the headings of $T_1,\ldots ,T_n$ in the obtained tour.

The open Dubins tours are computed by the technique introduced in Sect. 2 to solve problems of type (II). If the complete order $T_1,T_2,\ldots ,T_n$ is determined then a shortest closed Dubins tour is determined using the technique for problem (IV). Note that the algorithm does not extend a frozen path (as Nearest Neighbor does), but adds a new target to the order in each iteration. The headings of the targets may change in the next iteration. The final headings $h_1,\ldots ,h_n$ are determined in the last step.

As it turns out, the algorithm is practicable for a relatively small number of targets. However, the running time gets quite extensive if the number of targets is high. The results indicate that, when adding a new target, the headings of the last targets in the order change, whereas in most cases the headings of the first targets in the order remain as they are. In order to reduce the computation time, we consider only the last k targets in the order when optimizing the headings. The previous targets in the order are not used, i.e. their headings remain unchanged.

Algorithm:Greedy-k-extend

• 1. Determine an order $T_1, T_2,\ldots , T_k$ using step (1) and (2) of algorithm

  Greedy-extend.

  Let $h_1$ denote the heading of $T_1$ in the associated open Dubins tour.

• 2. For $p = k$ to $n-1$ do

  Choose the next target $T_{p+1}$ in such a way that the open Dubins tour

  through $T_{p-k+1} ,\ldots , T_p ,T_{p+1}$ with predefined heading $h_{p-k+1}$ in $T_{p-k+1}$

  is as short as possible.

  Let $h_{p-k+2}$ denote the heading of $T_{p-k+2}$ in the obtained tour.

• 3. Find a shortest possible open Dubins tour through $T_{n-k+1},\ldots ,T_n,T_1$

  with predefined headings $h_{n-k+1}$ in $T_{n-k+1}$ and $h_1$ in $T_1$.

  Let $h_{n-k+2},\ldots ,h_n$ denote the headings of $T_{n-k+2},\ldots ,T_n$ in the obtained

  tour.

After step (1) we have k targets fixed in an order. Only the heading of the first target is frozen. In each iteration of step (2) we have to calculate $n-p$ open Dubins tours consisting of $k+1$ targets, namely the last k targets from the already fixed order plus one target from the $n-p$ not yet included targets. The tours are calculated using the technique for problem (III) where the heading of the start target is fixed. This means that k headings are free. At the end of each iteration we freeze one further heading, namely the heading of the second target of the shortest tour. This target with the associated heading serves as the start target in the next iteration. In step (3) we close the tour by calculating an open Dubins tour consisting of the last k targets and the first target of the order. This is done using technique (I) where the headings of the first and last target are predefined. Here $k-1$ free headings have to be optimized.

Fig. 8

Example for algorithm Greedy-3-extend

It is worth noting that Greedy-1-extend turns into the Nearest Neighbor method if the discretization of the headings is infinitely fine. Figure 8 shows the single stages of algorithm Greedy-3-extend in a scenario with 7 targets and turning radius 0.5. The start target of each iteration is marked in green color. The first subfigure shows the result of step (1), the next four plots the iterations of step (2). The last plot shows the closure of the tour.

Fig. 9

Computational results for extension algorithms

The performance of the algorithms, tested on the random instances of Sect. 3, is illustrated in Fig. 9 with the solutions of the ETSP as a benchmark. The headings are discretized with a resolution of $10^{{\circ }}$. The algorithms achieve a clear improvement of the tour lengths compared to the Nearest Neighbor Heuristic. The gap increases even further with the number of targets. The improvement is about 15% for turning radius 0.1 and 25% for larger turning radii. It is remarkable that Greedy-3-extend on average provides only slight improvements compared to Greedy-2-extend. Further improvements obtained by increasing the value of k or by applying algorithm Greedy-extend are almost negligible. On the other side, the running time of the latter methods increase significantly with k. For instance, Greedy-3-extend requires more than twice the running time of Greedy-2-extend. Algorithm Greedy-extend is extremely time-consuming such that the test cases have been limited to 80 targets. The results clearly indicate that the additional computational effort is not justified.

5 Insertion algorithms

The following algorithms are motivated by a class of methods for the TSP known as insertion algorithms, see e.g. Lawler et al. (1985). The algorithms start with a closed subtour consisting of few targets and extend this tour by inserting the remaining targets one after the other until all targets have been inserted. The methods can be classified according to how the initial tour is constructed, how the next target to be inserted is chosen, and where the chosen target is inserted.

The starting tour is usually some tour consisting of three targets. A new target is inserted into the tour at a position that causes the minimum increase in the length of the tour. The major difference between the insertion algorithms is the order in which the targets are inserted. The nearest and farthest insertion algorithms, for instance, insert the target whose minimal distance to a target of the tour is minimal or maximal. The cheapest insertion algorithm chooses a target whose insertion causes the lowest increase in the length of the tour.

We try to adapt these algorithms to the DTSP. Given a closed Dubins tour consisting of targets $T_1,\ldots ,T_p$, a new target can be inserted at p different positions, namely between $T_1$ and $T_2$, between $T_2$ and $T_3$, etc., or between $T_p$ and $T_1$. The following algorithmic scheme selects a new target according to some strategy and inserts it such that the resulting tour is as short as possible.

Algorithm:Greedy-insert

• 1. Start with an arbitrary target $T_1$.

• 2. For $p = 1$ to $n-1$ do

  Choose a target T not yet belonging to the Dubins tour $T_1 ,\ldots , T_p$

  according to the selected strategy (Random / Nearest / Farthest).

  Determine a position in the tour such that the closed Dubins tour

  through $T_1 ,\ldots ,T_p$ and T is as short as possible.

  Rename the targets to $T_1,\ldots ,T_{p+1}$ according to the order of the obtained

  tour.

• 3. Let $h_1,\ldots ,h_n$ denote the headings of $T_1,\ldots ,T_n$ in the obtained tour.

The closed Dubins tours are determined using technique (IV) from Sect. 2. Note that the headings of all targets are free, i.e. the headings may change in each iteration. Due to the large number of tours to be computed, the algorithm is rather time-consuming and applicable only for scenarios of modest size. The following enhancements do not recalculate the whole tour in each iteration, but restrict themselves to a small portion of the tour around the inserted target. The methods differ in the number of targets that are considered for recalculation.

Given a Dubins tour $T_1,\ldots ,T_p$ with headings $h_1,\ldots ,h_p$ we denote with $d(T_i,T_{i+1})$ the length of the subtour between the targets $T_i$ and $T_{i+1}$ (with indices modulo p). For a target T not yet belonging to the tour let $d_T(T_i,T_{i+1})$ denote the length of the shortest possible open Dubins tour from $T_i$ to $T_{i+1}$ via T with fixed headings $h_i$ in $T_i$ and $h_{i+1}$ in $T_{i+1}$ and free heading in T. Then

$$\begin{aligned} \varDelta _T(T_i,T_{i+1})=d_T(T_i,T_{i+1})-d(T_i,T_{i+1}) \end{aligned}$$

is the increase of the tour length if T is inserted between $T_i$ and $T_{i+1}$ without changing the headings of the targets. We choose the insert position for T in such a way that the increase of the tour length is minimal. This approach inserts a new target leaving the whole tour unchanged except the connection between $T_i$ and $T_{i+1}$.

The following relaxation modifies the headings of few targets that are adjacent to the inserted target. For a Dubins tour $T_1,\ldots ,T_p$ with headings $h_1,\ldots ,h_p$ let $d(T_{i-k+1},T_{i+k})$ denote the length of the subtour between $T_{i-k+1}$ and $T_{i+k}$ and $d_T(T_{i-k+1},T_{i+k})$ the length of the shortest possible open Dubins tour through $T_{i-k+1},\ldots ,T_i,T,T_{i+1},\ldots ,T_{i+k}$ with predefined heading $h_{i-k+1}$ in $T_{i-k+1}$ and $h_{i+k}$ in $T_{i+k}$ (again with all indices modulo p). Then

$$\begin{aligned} \varDelta _T(T_{i-k+1},T_{i+k})=d_T(T_{i-k+1},T_{i+k})-d(T_{i-k+1},T_{i+k}) \end{aligned}$$

again describes the increase of the tour length if T is inserted between $T_i$ and $T_{i+1}$. Now the headings of $T_{i-k+1}$ and $T_{i+k}$ remain fixed but the headings of all targets in between are free. The length $d_T(T_{i-k+1},T_{i+k})$ of the open Dubins tour is calculated using technique (I) from Sect. 2. This approach provides a local change of the tour around the inserted target. Here is a more formal description:

Algorithm:Greedy-k-insert

• 1. Start with an initial Dubins tour $T_1,\ldots ,T_k$ with headings $h_1,\ldots ,h_k$.

• 2. For $p = k$ to $n-1$ do

  Choose a target T not yet belonging to the Dubins tour $T_1 ,\ldots , T_p$

  according to the selected strategy (Random / Nearest / Farthest).

  Determine a position in the tour such that the increase $\varDelta _T(T_{i-k+1},T_{i+k})$

  of the tour length is as short as possible.

  Rename the targets to $T_1,\ldots ,T_{p+1}$ according to the order of the

  obtained tour with headings $h_1,\ldots ,h_{p+1}$.

The start tour is generated using algorithm Greedy-insert. Algorithm Greedy-1-insert considers only one free heading for the inserted target. Greedy-2-insert allows two more free headings for the predecessor and successor. Greedy-3-insert has five free headings, for the inserted target and two predecessors and two successors. Generally, Greedy-k-insert (with its versions Random-k-insert, Nearest-k-insert and Farthest-k-insert) allows $2k - 1$ free headings.

The following algorithm tries to simultaneously find the most promising target and position in each iteration. It computes a closed Dubins tour for every target not yet belonging to the tour and for each possible insert position and chooses the target and position providing the shortest tour. As above, the methods differ in the number of free headings when inserting a target.

Fig. 10

Example for algorithm Cheapest-2-insert

Algorithm:Cheapest-k-insert

• 1. Start with an initial Dubins tour $T_1,\ldots ,T_k$ with headings $h_1,\ldots ,h_k$.

• 2. For $p = k$ to $n-1$ do

  Choose a target T not yet belonging to the Dubins tour $T_1 ,\ldots , T_p$

  and a position for T in the tour such that the increase $\varDelta _T(T_{i-k+1},T_{i+k})$

  of the tour length is as short as possible.

  Rename the targets to $T_1,\ldots ,T_{p+1}$ according to the order of the

  obtained tour with headings $h_1,\ldots ,h_{p+1}$.

The idea of algorithm Cheapest-2-insert is demonstrated in Fig. 10. The scenario contains the same set of targets as used in Fig. 8. The initial tour consisting of three targets is obtained by two iterations of Cheapest-insert. The latter algorithm leaves all headings free and is not explicitly formulated here. The following four iterations of Cheapest-2-insert add the remaining targets. The dashed lines mark the part of the tour that remains unchanged in the actual iteration. The inserted targets are highlighted in green color.

Fig. 11

Computational results for insertion algorithms

The performance of Greedy-k-insert and Cheapest-k-insert for $k=1,2$ and for a $10^{{\circ }}$ resolution of the headings is presented in Fig. 11. We can observe big improvements from $k=1$ to $k=2$, independent of the turning radius and the selected strategy. Results for higher values of k allowing five or more free headings are not included in the figure since the associated algorithms do not show substantial improvements but increase the computer running time by a high factor. The same holds for the algorithms Greedy-insert and Cheapest-insert where the headings of all targets are free in each iteration.

It turns out that the performance is strongly depending on the turning radius of the vehicle. If the radius is small then algorithm Farthest-2-insert clearly outperforms all other methods. Furthermore, Random-2-insert is superior to Cheapest-2-insert and Nearest-2-insert. These results are in accordance with practical experience obtained for the insertion heuristics of the TSP (see Lawler et al. 1985). However, the behavior completely changes if the turning radius increases to 0.5. Now Farthest-2-insert seems inferior to the other methods with Cheapest-2-insert appearing as the most promising approach. For turning radius 1.0 we observe only small differences between the algorithms, again with slight advantages for Cheapest-2-insert.

6 Performance and runtime analysis

In the previous sections we introduced a number of new heuristic algorithms for the DTSP (see the summary in Table 2), evaluated their performance depending on the turning radius of the vehicle, and showed that they compete favorably against standard methods known from the literature, including the Alternating Algorithm and the Nearest Neighbor method. A further step to demonstrate the capability of the new heuristics is to compete with an algorithm proposed by Le Ny et al. (2012) which is regarded as one of the leading methods for the DTSP. To gain an overall picture and provide a concluding assessment we consider the quality of the solutions versus the running time of the algorithms.

Table 2 Summary of proposed algorithms

The algorithm of Le Ny et al. (2012) defines a set of m possible headings at each target and constructs a graph with n clusters corresponding to the n targets, where each cluster contains m vertices corresponding to the choice of the headings. Then the Dubins distances are computed between all configurations corresponding to pairs of vertices in distinct clusters. Now the task is to find a tour through the n clusters which contains exactly one vertex in each cluster. This problem is known as the Generalized Asymmetric Traveling Salesman Problem (GTSP) and can be reduced to a standard asymmetric traveling salesman problem (ATSP) over $n \cdot m$ vertices.

Fig. 12

Computational results for DTSP algorithms

We apply the algorithm with 5 discretization levels of the headings, evenly distributed in the interval $[0, 2\pi ]$. Given a set of 100 targets, this provides an ATSP with 500 vertices. The solution of such an ATSP requires about half a minute using the Lin–Kernighan heuristic, see Helsgaun (2000). Clearly, the performance of the algorithm can be improved by increasing the discretization levels. However, this is at the expense of significantly increased computation time. For example, increasing the number of discretization levels to 10 will more than double the time. For larger scenarios with several hundreds or even thousands of targets, the method will soon require hours of running time. For that reason the algorithm is only of limited use for processing very large instances of the problem.

Fig. 13

Running time for DTSP algorithms

The quality of the solutions and the running time of the most promising algorithms for the DTSP are summarized in Figs. 12 and 13. For turning radius 0.1, the Optimized Headings Algorithm turns out to be clearly superior to all other methods regarding performance. This appears plausible since the optimal order of the ETSP should provide a good solution of the DTSP whenever the turning radius is small compared to the distance of the targets. The computation time is far below 10 s for a scenario with 100 targets, including the time to solve the associated ETSP. The method with lowest running time is Farthest-1-insert, however with rather modest quality of the solutions. The extension algorithms are not competitive for small turning radius.

The Optimized Headings Algorithm clearly outperforms GTSP. As mentioned before, the results of GTSP can be improved by increasing the number of headings. Given 100 targets, a $10^{\circ }$ discretization of the headings as used by the Optimized Headings Algorithm provides an ATSP with 3600 instead of 500 vertices, implying exploding computation time. The running time of the Optimized Headings Algorithm remains low compared to GTSP since the former is based on an ETSP with 100 vertices only, along with quickly solvable shortest path problems in a network with less more than 3600 vertices.

Fig. 14

Tours obtained by algorithms Greedy-2-extend and Cheapest-2-insert

For turning radius 0.5 there are several methods with similar performance. While the insertion algorithms perform slightly better for less than 50 targets, the extension algorithms are superior for larger scenarios. In the first case Cheapest-2-insert appears to be the best choice, replaced by Greedy-3-extend in the second case. However, Cheapest-2-insert is much more time-consuming than Greedy-3-extend. It seems that algorithm Greedy-2-extend provides the best trade-off between quality of solutions and runtime. Algorithms based on solutions of the ETSP perform poorly for large turning radii.

For turning radius 1.0 we again find several methods of similar performance, with the extension algorithms seeming slightly superior to the insertion algorithms. Greedy-3-extend appears as the best method, however with significantly higher running time than Greedy-2-extend. While the running time of Greedy-2-extend marginally exceeds GTSP for less than 80 targets, it reverses for larger scenarios. The gap substantially increases with the number of targets. In summary, algorithm Greedy-2-extend again constitutes the best compromise between running time and quality of the solution.

Our experience indicates that, in general, insertion algorithms tend to work better than extension algorithms if the turning radius is small. Figure 14 shows the tours obtained by algorithms Cheapest-2-insert and Greedy-2-extend in a scenario with 100 targets, for a vehicle with turning radius 0.1. The increase of the tour lengths when adding new targets reveals the typical behavior of the algorithms. While Cheapest-2-insert shows a more or less even increase of the tour length with few and moderate peaks only, algorithm Greedy-2-extend proceeds extremely well in the first phase but shows large peaks at the end. The reason is that single targets or groups of targets lie outside the growth corridor of the algorithm and must be connected to the actual subtour by long Dubins paths.

This also explains the performance of algorithm Greedy-2-extend when the size of the scenario grows from 10 to 20 targets (see Fig. 12a). While the algorithm operates well for very small test cases, the number of forgotten targets increases for larger test cases. This requires several long connections to add those targets and deteriorates the quality of the solutions. Moreover, the last step of the algorithm which closes the open Dubins tour, often requires a long Dubins path leading back to the start point of the tour.

Fig. 15

Tours obtained by algorithms Greedy-2-extend and Cheapest-2-insert

A further conclusion is that, for large turning radii, the extension algorithms seem superior to the insertion methods. A typical example based on the same scenario as above, but with turning radius 1.0, is presented in Fig. 15. The tour obtained by Greedy-2-extend shows long series of targets with modest increase of the tour lengths, but also a certain number of peaks. These correspond to targets which are located far away from the last target of the subtour, or to targets which are added by realizing loops. Cheapest-2-insert contains much more and higher peaks. This indicates that inserting targets into a closed subtour seems more difficult than adding them to an open subtour. The final tour contains more and longer loops. Note that the first peak belongs to the initial tour which consists of two targets only. This tour resembles a circle of circumference $2\pi$.

Fig. 16

Tours obtained by Optimized Headings Algorithm

Fig. 17

Tours obtained by algorithms Greedy-2-extend and Nearest-2-insert

The new methods are also applicable to large-scale scenarios with thousand and more targets, keeping the running time within reasonable limits. The tours for a scenario with 1000 targets in Fig. 16 have been generated by the Optimized Headings Algorithm, with a $10^{\circ }$ discretization of the headings. For turning radius 0.05 the tour strongly resembles the optimal solution of the ETSP where all targets are connected by straight lines. There are only minor deviations and a restricted number of short loops. The ratio of the tour lengths of DTSP and ETSP is 1.25. If the turning radius is increased to 0.1 then we observe a large number of loops. This is due to the fact that the turning radius gets large compared to the average distance of consecutive targets. It is frequently not possible to directly connect two targets. The ratio of the tour lengths increases to 2.40.

Figure 17 shows the tours of the same scenario obtained by algorithms Greedy-2-extend and Nearest-2-insert, again with a $10^{\circ }$ resolution of the headings. The tour of Greedy-2-extend shows many targets in a row with short connections. Compared to the Optimized Headings Algorithm there is only a small number of loops. On the other hand, the algorithm generates several long straight segments to other subregions of the operational area not yet processed by the algorithm. One of the straight segments closes the tour by connecting the first with the last target. The tour of Nearest-2-insert seems to be somewhat more winding but does not contain any long straight path segments. Both algorithms perform significantly better than the Optimized Headings Algorithm with a similar tour length ratio of slightly above 1.8.

The running time of the Optimized Headings Algorithm is about 80 s, including the time for solving the associated ETSP. Greedy-2-extend is marginally faster, whereas Nearest-2-insert requires almost 4 min. For comparison, solving the corresponding GTSP with a discretization level that allows solutions of similar quality, takes many hours.

7 Conclusion

The Dubins traveling salesman problem is a variation of the traveling salesman problem where the length of a tour has to be minimized in which a kinematically constrained vehicle visits a set of targets. This paper introduces new classes of heuristic algorithms to solve this problem. The algorithms are based on a technique that optimizes headings by discretization and finding shortest paths in auxiliary networks. The order of the targets is obtained by solving an Euclidean traveling salesman problem, or by applying different strategies that successively extend an open subtour by one target or insert a new target into a closed subtour. A comparative study shows that the algorithms are able to compete with state-of-the-art algorithms in terms of performance. A major benefit is that the algorithms are time-efficient and applicable for very large scenarios, hence overcoming limitations of other methods.

The proposed methods belong to the class of constructive algorithms that build a solution according to a predefined set of rules. In future work we intend to extend our investigations to improvement algorithms that start from a feasible tour and try to iteratively improve the tour by applying small changes. Such local search algorithms could be inspired by the well known 2-opt and 3-opt methods for the traveling salesman problem, or by metaheuristics including genetic algorithms, tabu search, simulated annealing, and others.