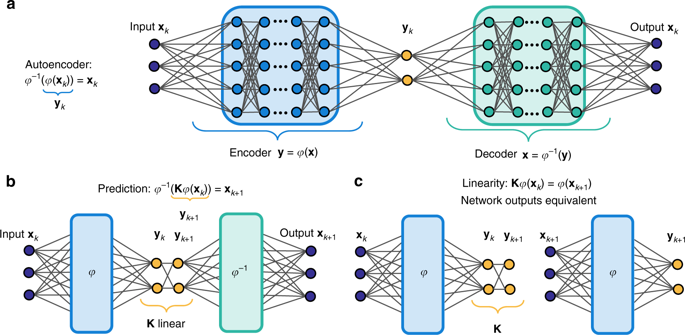
Identifying coordinate transformations that make strongly nonlinear dynamics approximately linear has the potential to enable nonlinear prediction, estimation, and control using linear theory. The Koopman operator is a leading data-driven embedding, and its eigenfunctions provide intrinsic coordinates that globally linearize the dynamics. However, identifying and representing these eigenfunctions has proven challenging. This work leverages deep learning to discover representations of Koopman eigenfunctions from data. Our network is parsimonious and interpretable by construction, embedding the dynamics on a low-dimensional manifold. We identify nonlinear coordinates on which the dynamics are globally linear using a modified auto-encoder. We also generalize Koopman representations to include a ubiquitous class of systems with continuous spectra. Our framework parametrizes the continuous frequency using an auxiliary network, enabling a compact and efficient embedding, while connecting our models to decades of asymptotics. Thus, we benefit from the power of deep learning, while retaining the physical interpretability of Koopman embeddings.

中文翻译：

---

非线性动力学通用线性嵌入的深度学习。


识别使强非线性动力学近似线性的坐标变换有可能使用线性理论实现非线性预测、估计和控制。 Koopman 算子是一种领先的数据驱动嵌入，其特征函数提供了全局线性化动力学的内在坐标。然而，识别和表示这些特征函数已被证明具有挑战性。这项工作利用深度学习从数据中发现库普曼本征函数的表示。我们的网络是简约的并且可以通过构造来解释，将动态嵌入低维流形上。我们使用改进的自动编码器来识别非线性坐标，在该坐标上动力学是全局线性的。我们还概括了库普曼表示，以包括一类普遍存在的具有连续谱的系统。我们的框架使用辅助网络对连续频率进行参数化，从而实现紧凑且高效的嵌入，同时将我们的模型与数十年的渐进连接起来。因此，我们受益于深度学习的力量，同时保留了库普曼嵌入的物理可解释性。