Abstract
In the present paper, we consider a class of quasilinear wave equations on a smooth, bounded domain. We discretize it in space with isoparametric finite elements and apply a semi-implicit Euler and midpoint rule as well as the exponential Euler and midpoint rule to obtain four fully discrete schemes. We derive rigorous error bounds of optimal order for the semi-discretization in space and the fully discrete methods in norms which are stronger than the classical \(H^1\times L^2\) energy norm under weak CFL-type conditions. To confirm our theoretical findings, we also present numerical experiments.
Similar content being viewed by others
1 Introduction
In the present paper, we consider the quasilinear wave equation
for \( t\in [0,T]\), \(x \in \varOmega \subset {\mathbb {R}}^N\), \( N=1, 2, 3.\) We assume the domain \(\varOmega \) to be bounded with a sufficiently regular boundary and impose homogeneous Dirichlet boundary conditions. We discretize (1.1) in space using isoparametric finite elements and employ for the time discretization a semi-implicit Euler and midpoint rule as well as an exponential Euler and midpoint rule. We derive error bounds in norms stronger than the standard energy \(H^1 \times L^2\)-norm.
The first wellposedness results for a large class of quasilinear wave type equation were given by Kato in [25, 26]. This approach was refined in [11] for the problem (1.1) to account for the state-dependent norms necessary in the analysis. A typical example in nonlinear acoustics is the model \(\lambda (u) = 1 - u^m\) for some \(m\in {\mathbb {N}}\). Hence, in order to ensure \(\lambda (u)>0\), a key ingredient in the proof is to establish pointwise bounds on \(u\) (as well as \(\partial _tu\)), often via Sobolev’s embedding \(H^2\hookrightarrow L^\infty \). To inherit this property in the spatial discretization, we need pointwise bounds on the numerical approximations in the error analysis. However, since the finite elements space is not \(H^2\)-conforming, we cannot follow the above approach.
So far in the literature, bounds in \(H^1 \times L^2\) are shown by inverse estimates which yield a factor \(h^{-\beta }\) for some \(\beta \ge 1\) with the spatial mesh width h. This induces unsatisfactory CFL-type conditions and excludes linear finite elements. In contrast with this, we adapt the idea from the wellposedness and perform the error analysis not in the energy space \(H^1 \times L^2\), but employ a discrete version of the \(H^2\)-norm. A discrete variant of Sobolev’s embedding and a suitably defined solution space for the numerical approximation allow us to remove lower bounds on the polynomial degree of the finite element space and significantly improve the CFL-type condition compared to the literature. For the temporal step size \(\tau \) and the spatial mesh width h, we show convergence in \(N=2\) under the restriction \(\tau \lesssim h^\alpha \), for any \(\alpha >0\), and in \(N=3\) we have \(\tau \lesssim h^{1/2 +\alpha }\) for the first-order methods in time and \(\tau \lesssim h^{1/4 +\alpha }\) for the second-order method. In addition, we fully remove the CFL-type condition for \(N=1\).
The strategy of the semi discrete proof relies on a bootstrap argument. We set up a suitable solution space for the numerical approximation and show that the initial value lies in this. Instead of the usual choice of interpolated initial values, we have to use a Ritz map for which we provide a computable alternative of the correct order. Since we are working with a finite-dimensional subspace, this directly yields local wellposedness up to some time \(t^*_h>0\). On this possibly short time interval, we prove convergence in the stronger norm and use this to extend \(t^*_h\) beyond T and to close the argument. For the fully discrete error bounds, this approach is generalized using an induction argument.
We give a brief overview of the literature on the numerical treatment of quasilinear wave equations. In the pioneering works [10, 24, 27, 37], existence of solutions to quasilinear and nonlinear evolution equations is established, and one can find approximation rates of the implicit and semi-implicit Euler method. Within an (extended) Kato framework, optimal order for these methods was achieved in [22] and rigorous error bounds for the time discretization by higher-order Runge–Kutta methods are derived in [23, 28].
Concerning the spatial discretization, the results in [21] yield optimal order of convergence for the equation (1.1), however, only for polynomials of degree greater than two. For the strongly damped Westervelt equation, continuous and discontinuous Galerkin methods were analyzed in [1, 34]. Very recently, mixed finite elements for the Kuznetsov and Westervelt equations were studied in [33].
In [31], error bounds for two variant of the midpoint rule are derived of optimal order, but only for polynomials of degree greater than two and under a stronger CFL-type condition compared to our results. In the case of one-dimensional wave equation subject to periodic boundary conditions, full discretization error bounds are established in [19]. A sophisticated energy technique combined with the properties of the spectral discretization yields convergence without a CFL-type condition.
For a slightly different quasilinear wave equation, optimal error bounds in \(L^2\) for continuous finite elements were considered in the literature. One-step methods of different order are analyzed in [3, 4, 17], and two-step methods are considered in [5]. For a class of linearly implicit single-step schemes as well as a linearly and a fully implicit two-step scheme, optimal error bounds are derived in [32]. However, all of these results require a CFL-type condition at least as strong as \(\tau \lesssim h\) and do not allow for linear finite elements. We expect that our technique can be generalized to these problems, but this will be part of future research.
The paper is organized as follows: We describe in Sect. 2 the analytical framework, the space discretization by isoparametric Lagrange finite element, and state our main results. The proof of the spatial convergence rates is given in Sect. 3, where we first reduce the main result to error bounds in a stronger energy norm which is established afterward. In Sect. 4, we extend this technique to the fully discrete case for the three presented methods. Certain stability estimates and the bounds on the defects are given in Sect. 5, and some postponed results are shown in Appendices A, B, C, and D.
1.1 Notation
In the rest of the paper, we use the notation
if there is a constant \(C>0\) independent of the spatial parameter h and the time step size \(\tau \) such that \(a \le Cb\). For the sake of readability, we introduce the notation \(t^{n} = n \tau \) and
for an arbitrary time-dependent, continuous object x(t). If it is clear from the context, we write \(L^p\) instead of \(L^p(\varOmega )\) or \(L^p(\varOmega _h)\).
2 General Setting
For a bounded domain \(\varOmega \subset {\mathbb {R}}^N\), \(N=1,2,3\), with boundary \(\partial \varOmega \in C^{s}\), \(s\in {\mathbb {N}}\), we study the quasilinear wave Eq. (1.1) with homogeneous Dirichlet boundary conditions and initial values
We note that the operator \(-\mathrm {\Delta }\) is positive and self-adjoint on \(L^2(\varOmega )\), and we define the spaces \(H= L^2(\varOmega )\) and \(V= H_0^1(\varOmega )\). Throughout the paper, we impose the following conditions on the function \(\lambda \) and \(g\). Additional requirements are stated in our main results.
Assumption 2.1
- \((\lambda _1)\):
-
The function \(\lambda :{\mathbb {R}}\rightarrow {\mathbb {R}}\) satisfies \(\lambda \in C^2({\mathbb {R}},{\mathbb {R}})\).
- \((\lambda _2)\):
-
There is some radius \({\widehat{r}}_\infty >0\) such that there is a constant \(c_{\lambda } = c_{\lambda } ({\widehat{r}}_\infty )>0\) such that
$$\begin{aligned} c_{\lambda }&\le \lambda (x), \quad |x| \le {{\widehat{r}}_\infty } . \end{aligned}$$ - \((g_1)\):
-
The function \(g:[0,T] \times {\overline{\varOmega }} \times {\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}\) satisfies \(g\in C^2([0,T] \times {\overline{\varOmega }} \times {\mathbb {R}}\times {\mathbb {R}},{\mathbb {R}})\).
- \((g_2)\):
-
For \(x \in \partial \varOmega \) and \(y=z=0\) it holds \( g(t,x,y,z) = 0\).
The conditions \((\lambda _1),(g_1)\) are structural assumptions which allow us to show crucial stability estimates. The lower bound in \((\lambda _2)\) prevents the degeneracy of (1.1). The main effort in the discretization and error analysis is to ensure that this condition is inherited. We note that condition \((g_2)\) implies in particular that for \(u, v \in V\) one has \(g(t,u,v)\in V\), and that all conditions are already required for the wellposedness. We recall an example for the quasilinear problem (1.1) given in [11].
Example 2.2
Let \(K \in C^4({\mathbb {R}},{\mathbb {R}})\) with \(1 + K'(0)> 0 \) and consider the problem
for example, with the Kerr model \(K(z) = \alpha z^3\) for \(\alpha \in {\mathbb {R}}\). If we rewrite it in the form (1.1), we obtain
which satisfy Assumption 2.1. Denoting the fractional powers of the Laplacian by \({\mathcal {H}}_k {:}{=}{\mathcal {D}}\bigl ( (-\varDelta )^{k/2} \bigr )\), under suitable smallness assumptions on the initial values, the existence of a solution
is shown in [11, Thm. 4.1]. \(\lozenge \)
Equivalently to (1.1), we consider the quasilinear wave equation in first-order formulation
with initial value \(y(0) = y^{0}\) in the product space \(X= V\times H\), and
Remark 2.3
The assumption on the regularity of the boundary is not essential in the error analysis, which also works on a convex, polygonal domain. Hence, one could apply a conforming finite element method. However, since the wellposedness of quasilinear equations requires a regular boundary, we will work in the nonconforming framework in the following.
2.1 Space Discretization
We study the nonconforming space discretization of (2.1) based on isoparametric finite elements. For further details on this approach, we refer to [15, 16]. In particular, we introduce a shape-regular and quasi-uniform triangulation \({\mathcal {T}}_h\), consisting of isoparametric elements of degree \(k \in {\mathbb {N}}\) and let \(\partial \varOmega \in C^{k+1}\). The computational domain \(\varOmega _h\) is given by
where the subscript h denotes the maximal diameter of all elements \(K \in {\mathcal {T}}_h\). In the following, we require that h is sufficiently small such that all cited results below hold true. We note that the smallness only depends on the geometry of the domain \(\varOmega \) and the polynomial degree k. The semi-discrete approximations are given by \(u_h(t) \approx u(t)\) and \(v_h(t) \approx \partial _tu(t)\). Based on the transformations \(F_K\) mapping the reference element \({\widehat{K}}\) to \(K \in {\mathcal {T}}_h\), we introduce the finite element space of degree k
Here, \({\mathcal {P}}^k({\widehat{K}})\) consists of all polynomials on \({\widehat{K}}\) of degree at most k. The discrete approximation spaces are given by
and we set \(X_h= V_h\times H_h\).
Following the detailed construction in [16, Sec. 5], we introduce the lift operator \({\mathcal {L}}_h:H_h\rightarrow H\). In particular, for \(p \in [1,\infty ]\) there are constants \(c_{p}, C_{p} > 0\) with
cf. [16, Prop. 5.8]. By construction, the boundary nodes of \(\varOmega _h\) lie on \(\partial \varOmega \) and zero boundary conditions are preserved by \({\mathcal {L}}_h\), see [16, Sec. 8.5]. Further by [15, Sec. 4], the lift preserves values at the nodes, i.e., in particular
where we denote the nodal interpolation operator by \(I_h:C_0(\varOmega ) \rightarrow V_h\) and, enriching the space \(W_h\) by basis functions corresponding to the boundary nodes, its extension \(I_h^{e}:C(\varOmega ) \rightarrow C(\varOmega _h)\). Further, we define the adjoint lift operators \({\mathcal {L}}_h^{H*}:H\rightarrow H_h\) and \({\mathcal {L}}_h^{V*}:V\rightarrow V_h\) by
We note that in the conforming case, i.e., \(\varOmega = \varOmega _h\), \({\mathcal {L}}_h^{H*}\) and \({\mathcal {L}}_h^{V*}\) coincide with the \(L^2\)-projection \(\pi _h:L^2(\varOmega _h) \rightarrow H_h\) and the Ritz projection \(R_h:H^1_0(\varOmega _h) \rightarrow V_h\), respectively, given by
For \(u_h,v_h\in V_h\) we define the discrete operator \(\lambda _h(u_h) :H_h\rightarrow H_h\) and the discrete right-hand side \(g_h\) by
respectively. Denoting by \(I_h^{\varOmega _h}:C(\varOmega _h) \rightarrow V_h\) the nodal interpolation operator with the same nodes as \(I_h\), we have by (2.3) the identity \( I_h\lambda ( {\mathcal {L}}_hu_h) = I_h^{\varOmega _h}\lambda ( u_h)\) and similarly for \(g_h\). The first-order counterparts of (2.6) are given by
Moreover, we show in Sect. 2.5 that under certain assumption on \(u_h\in V_h\) there exists a modified \(L^2\)-projection \(Q_h(u_h) :L^2(\varOmega _h) \rightarrow V_h\) such that the inverse of \(\lambda (u_h)\) is given by
Finally, we introduce the operators \(\mathrm {\Delta }_h:V_h\rightarrow H_h\) and \(\textrm{A}_h:X_h\rightarrow X_h\) given by
Note that \(\mathrm {\Delta }_h\) is symmetric and \(\textrm{A}_h\) is skew-symmetric with respect to \(H_h\) and \(X_h\), respectively, but they are not uniformly bounded with respect to h. The spatially discrete quasilinear wave equation in first-order formulation then reads
with the initial value \(y_h(0) = y_h^{0}\).
2.2 Choice of the Initial Value
As already mentioned, an appropriately chosen initial value is a key ingredient in the subsequent error analysis. An ideal initial value would include the adjoint lift operator \({\mathcal {L}}_h^{V*}\) defined in (2.4b). However, in order to compute this operator, integrals over the exact domain \(\varOmega \) have to be evaluated.
We thus propose an alternative that involves to use a finite element space of degree \(k' \ge k+1\) denoted by \({\widetilde{V}}_h\) over the computational domain \({\widetilde{\varOmega }}_h\). Further, let \({\widetilde{{\mathcal {L}}}}_h\) and \({\widetilde{I}}_h\) be the corresponding lift and interpolation operators. Then, for \(u\in H^2\), we define the modified Ritz map \({\widetilde{R}}_hu\) via
We use this operator together with the interpolation to define the initial value by
In Appendix A, we prove the following approximation property and discuss the computation of \({\widetilde{R}}_h\).
Proposition 2.4
For \(u^{0} \in H^{k+2}(\varOmega ) \cap V\), the difference of the adjoint lift \({\mathcal {L}}_h^{V*}\) defined in (2.4b) and \({\widetilde{R}}_h\) in (2.11) satisfies the bound
where the constant C is independent of h.
We emphasize that the precise construction of the initial value is not important in the error analysis, but only the bounds obtained in Proposition 2.4. Hence, if we can compute the adjoint lift exactly, which is the Ritz projection in the conforming case, then one can also choose \(u_h^{0} = {\mathcal {L}}_h^{V*}u^{0}\). However, we cannot make the standard choice \(u_h^{0} = I_hu^{0}\), since this would imply the statement of Proposition 2.4 only with k instead of \(k+1\).
2.3 Main Result for the Semi-Discretization in Space
Before we state our main error bounds, we chose some exponent \({p^*}\), depending on the dimension \(N= 1,2,3\), as
This choice in particular implies the Sobolev embeddings
Our first main result gives an error bound on the spatially discrete solution defined in (2.10), and the proof is given in Sect. 3. Recall the fractional powers of the Dirichlet Laplacian denoted by \({\mathcal {H}}_k {:}{=}{\mathcal {D}}\bigl ( (-\varDelta )^{k/2} \bigr )\).
Theorem 2.5
Let \(\partial \varOmega \in C^{k+1}\), and Assumption 2.1 hold. Further, let the solution \(u\) satisfy
and choose the initial value (2.12). Then, there is \(h_0>0\) such that for all \(h \le h_0\), it holds for \(t \in [0,T]\)
with a constant \(C>0\) which is independent of h.
Using (2.14), the theorem implies convergence in the maximum norm for \(u_h\) and in \(L^{p^*}\) for \(v_h\) and is in particular applicable to linear finite elements. We note that the results from the literature so far had the limitation \(k\ge 2\).
2.4 Main Results for Full Discretization
We further discuss the convergence of four different fully discrete schemes. We recall that by \(\tau >0\) we denote the time step size and define for \(n=0,\ldots ,N\) the times \(t^{n} = n \tau \), with \(T = N \tau \). The fully discrete approximations are given by \(u_h^{n} \approx u(t^{n})\) and \(v_h^{n} \approx \partial _tu(t^{n})\). The proofs of the convergence results are given in Sect. 4.
2.4.1 Semi-Implicit Euler Method
For a variant of the implicit Euler method, we introduce the discrete derivative
and consider as in [10, 22] the semi-implicit Euler method
by freezing the nonlinear parts at the numerical approximation in the last step. The computation of the next approximation thus only requires the solution of a linear system. For the analysis, we impose the following weak CFL-type condition
with \({p^*}\) from (2.13) and some arbitrary \(\varepsilon _0>0\). This yields the following convergence result.
Theorem 2.6
Let \(\partial \varOmega \in C^{k+1}\), and Assumption 2.1 hold. Further, let the solution \(u\) in addition to (2.15) satisfy
and choose the initial value (2.12). Then, under the condition (2.18) there are \(h_0,\tau _0 > 0\) such that for all \(h \le h_0\) and \(\tau \le \tau _0\), it holds for \(0 \le t^{n} \le T\)
with a constant \(C>0\) which is independent of h and \(\tau \).
We emphasize that the CFL-type condition in (2.18) is essentially no restriction for \(N=2\) since \({p^*}\) can be chosen arbitrarily large due to (2.13). For \(N=3\), the CFL roughly yields \(\tau \lesssim h^{1/2+\varepsilon }\). However, even for \(k=1\), the error behaves as \(\tau + h\), and one would choose \(\tau \sim h\) anyway.
2.4.2 Semi-Implicit Midpoint Rule or Crank–Nicolson Scheme
As a second order in time method, we consider a variant of the midpoint rule proposed in [28]
with average \(y_h^{n+1/2}\) and extrapolation \({\bar{y}}_h^{n + 1/2}\) given by
The first approximation \(y^{1}\) is computed with the Euler method (2.17), and as before, in every time step only a linear system has to be solved. For the analysis of the second-order method, we can weaken the CFL-type condition compared to (2.18) and require only
Theorem 2.7
Let \(\partial \varOmega \in C^{k+1}\), and Assumption 2.1 hold. Further, let the solution \(u\) in addition to (2.15) satisfy
and choose the initial value (2.12). Then, under the condition (2.20) there are \(h_0,\tau _0>0\) such that for all \(h \le h_0\) and \(\tau \le \tau _0\), it holds for \(0\le t^{n} \le T\)
where C is independent of h and \(\tau \).
Since, there is again essentially no CFL-type condition for \(N=2\), we only discuss the case \(N=3\). We require \(\tau \lesssim h^{1/4+\varepsilon }\), whereas in [31] not only \(k\ge 2\) but also \( \tau \lesssim h^{3/4+\varepsilon } \) has to be imposed.
2.4.3 Exponential Euler Method
We turn to exponential methods which employ the variation-of-constants formula and an exact evaluation of the matrix exponential applied to a vector. For the approximation \(y_h^{n} \approx y(t^{n})\), we use the shorthand notation \({\textbf{A}}_h^{\hspace{-0.3mm}n} = \varLambda _h^{-1}(y_h^{n}) \textrm{A}_h\) and consider the method which was proposed in [12]
with the analytic function \(\varphi _1(z) = \int _0^1 e^{s z}\,ds\). We obtain the following error bound.
Theorem 2.8
Let \(\partial \varOmega \in C^{k+1}\), and Assumption 2.1 hold. Further, let the solution \(u\) satisfy (2.15), and choose the initial value (2.12). Then, under the condition (2.18) there are \(h_0,\tau _0>0\) such that for all \(h \le h_0\) and \(\tau \le \tau _0\), it holds for \(0 \le t^{n} \le T\)
where C is independent of h and \(\tau \).
We note that the CFL-type condition is the same as in the error bound of the semi-implicit Euler in Theorem 2.6.
2.4.4 Exponential Midpoint Rule
A second-order exponential variant is for example given by the exponential midpoint rule proposed in [12]. Using the notation in (2.19b), we define
and consider the scheme
Employing the techniques established for the proofs of Theorems 2.6 and 2.8, and combining them with the techniques in [12], allows for a convergence result as in Theorem 2.7 under the weaker CFL-type condition (2.20).
Theorem 2.9
Let \(\partial \varOmega \in C^{k+1}\), and Assumption 2.1 hold. Further, let the solution \(u\) in addition to (2.15) satisfy
and choose the initial value (2.12). Then, under the condition (2.20) there are \(h_0,\tau _0>0\) such that for all \(h \le h_0\) and \(\tau \le \tau _0\), it holds for \(0\le t^{n} \le T\)
where C is independent of h and \(\tau \).
2.5 Numerical Experiments
To illustrate our theoretical findings, we present some numerical experiments for the non-exponential methods. We first illustrate the optimality of our error bounds using a smooth solution and then consider the formation of a shock wave.
2.5.1 Smooth Solution
Let \(\varOmega = B_1(0) \subset {\mathbb {R}}^2\) be the two-dimensional unit sphere and consider Eq. (1.1) from Example 2.2 with \(\alpha = - \frac{1}{6}\) and data given by
where \(r^2 = |{\textbf{x}}|^2\). The additional forcing term \({\widehat{f}}\) is chosen such that the exact solution is given by
A simple calculation shows that the regularity assumptions of Theorems 2.5, 2.6, and 2.7 are satisfied. The scaling by a factor 10 is used to approximately normalize the \(W^{1,\infty }\)-norm of the solution \(u\).
2.5.2 Discretization
We discretize in space using the mass and stiffness matrices
where we denote by \((\varphi _i)_i\) the nodal basis of \(V_h\). Then, the discrete solution in (2.10) satisfies
by abusing the notation for the coefficient vectors and their corresponding function in \(V_h\). The Euler method in (2.17) is then given for \(n\ge 0\) by
where we abbreviate \(M_h^n = M_h \bigl (u_h^{n} )\). For the fully discrete midpoint rule, (2.19) is then given for \(n\ge 1\) by
denoting the extrapolations by \({\bar{u}}_h^{n + 1/2} = \frac{3}{2} u_h^{n} - \frac{1}{2} u_h^{n-1}\) and \({\bar{v}}_h^{n + 1/2} = \frac{3}{2} v_h^{n} - \frac{1}{2} v_h^{n-1} \), and the mass matrix by \(M_h^{n+1/2} = M_h \bigl ({\bar{u}}_h^{n + 1/2} ) \). For the step \(n=0\), we use the Euler scheme from above. We implemented the numerical experiments in C++ using the finite element library deal.II (version 9.4) [2, 6]. A precise description of the implementation can be found for example in [29, Ch. 6.5.1]. For the implementation of the initial value in (2.12), we refer to Appendix A. Concerning the computational costs, let us note that in each step the right-hand side as well as the mass matrix have to be assemble. The stiffness matrix is stored after assembling it before the time stepping. In addition, a linear system for the sparse matrix \(M_h + \frac{\tau ^2}{4} L_h\) has to be solved in each step using the conjugate gradient method. The codes written by Malik Scheifinger under the author’s supervision to reproduce the experiments are available at https://doi.org/10.35097/1792.
2.5.3 Numerical Results
For the problem described above, we performed experiments for the time and space discretization, where we used finite elements of order \(k=1,2,3\). In the error bounds of Sect. 2, for \(N=2\), the norm \(W^{1,p} \times H^1\) is used for \(p< \infty \) arbitrarily large. Hence, we chose \(p=\infty \) in our experiments, but note that the plots were qualitatively very similar for finite p. Since the computation of the lift of a finite element function is very laborious, and in application usually also not available, we do not compute the full error in the form \({\mathcal {L}}_hu- u_h\). Instead, in our numerical examples we consider the error
for the nodal interpolation operator \(I_h\) which is of the same order by the standard interpolation estimates. Note that in practice, one is only interested in \(u_h\), and the computation of the error here is only relevant to confirm our theoretical error bounds.
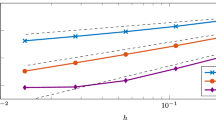
Left: error \({\textbf{E}}(0.8)\) of the semi-implicit midpoint rule (with time step size \(\tau = 8 \cdot 10^{-4}\) and \(\tau = 2.67 \cdot 10^{-4}\)) combined with finite elements of order \(k = 1,2,3\) plotted against the mesh width h. The dashed lines indicate order \(h^k\) for \(k=1,2,3\). Right: Error \({\textbf{E}}(0.8)\) of the semi-implicit Euler method and midpoint rule combined with finite elements of order \(k=3\) (\(h = 1.52 \cdot 10^{-2}\)) plotted against the time step size \(\tau \). The dashed lines indicate order 1 and 2
In the left part of Fig. 1, the convergence of the error with respect to the spatial mesh width h is shown when using the semi-implicit midpoint rule with \(\tau = 8 \cdot 10^{-4}\). We observe that for finite elements of order k the error converges with order k in space as predicted by Theorem 2.5 and 2.7 until the error for \(k=3\) is dominated by the error of the temporal approximation. For \(k=3\), we ran the same experiment again with the smaller time step size \(\tau = 2.67 \cdot 10^{-4}\) to remove this plateau. Running the same experiment with the semi-implicit Euler method instead of the midpoint rule yields a qualitatively similar picture. Due to slower convergence in time, the error already stagnates at about \(10^{-3}\).
In the right part of Fig. 1, we consider the convergence of the error with respect to the time step size \(\tau \) for the semi-implicit Euler method and midpoint rule. In space, we discretized with finite elements of order \(k=3\) and \(h = 1.52 \cdot 10^{-2}\) such that the spatial error is negligible. Aligning to Theorem 2.6, we observe convergence of order 1 in time for the Euler method and, confirming Theorem 2.7, convergence of order 2 for the midpoint rule.
2.5.4 Steepening Wave
In this second experiment, we consider the formation of a shock wave which is an often observed phenomenon in nonlinear waves. Since we are in a bounded domain, we force the wave to form a large gradient close to the origin. To this end, we chose our data by
where \(r^2 = |{\textbf{x}}|^2\). The additional forcing term \({\widehat{f}}\) is chosen such that the exact solution is given by
We observe that for \(\alpha t \rightarrow 1\), the maximum norm of \(\nabla u\) tends to infinity. We thus simulate up to the end time \(T = 1\) for different, increasing values of \(\alpha <1\), and in Fig. 2 we depicted the corresponding solutions at the end time. The discretization in space and time is performed as described in Sect. 2.4.1.
Plots of the (exact) shock wave solution given in (2.21) for the final time \(t = 1 \) and different values of \(\alpha = 0.6, 0.8, 0.9, 0.95\)
2.5.5 Numerical Results
We restrict ourselves to the approximation quality in the spatial discretization in this case and thus apply the semi-implicit midpoint rule with \(\tau = 8 \cdot 10^{-4}\) and linear and quadratic finite elements. We then use increasing values of \(\alpha = 0.6, 0.8, 0.9, 0.95\), which can be translated into simulating closer to the blow-up point \(\alpha t = 1\). We depicted the convergence in Fig. 3. In the linear case, we observe that we obtain a reasonable approximation for moderate values of \(\alpha \), which correspond to the smooth case. However, when a shock occurs, our method suffers from large errors due to the large gradient. Compared to the linear polynomials, using quadratic polynomials appears to be advantageous, not only because of the better resolution near the blow-up, but also because of smaller error constants. Nevertheless, in the quadratic case, the error constants become large for \(\alpha \rightarrow 1\) as well.
Error \({\textbf{E}}(1.0)\) of the semi-implicit midpoint rule (with time step size \(\tau = 8 \cdot 10^{-4}\)) combined with finite elements of order \(k=1\) (left) and order \(k=2\) (right) plotted against the mesh width h for the values of \(\alpha = 0.6,0.8,0.9,0.95\). The dashed lines indicate order h or \(h^2\), respectively
2.6 Additional Results for Isoparametric Finite Elements
In this section, we provide further estimates on the spatially discrete objects which are used throughout the paper. As shown in [16, Thm. 5.9], we have for the nodal interpolation operator for \(m \in \{0,1\}\), \(1 \le p \le \infty \), and \(1 \le \ell \le k\) the estimates
Further, by [9, Thm. 3.1.6] \(\ell =0\) is allowed for \(N< p \le \infty \). Another crucial property of the interpolation concerns the stability when applied to the product of functions. We give a proof in Appendix B.
Lemma 2.10
Let \(\psi _h \in V_h\), \(\delta >0\), and \(\varphi \in W^{1,N+\delta }(\varOmega )\). Then,
where the constant \(C>0\) is independent of h.
Concerning the adjoint lifts defined in (2.4), we show in Appendix B the following bounds for \(1\le \ell \le k \)
An interpolation argument between [16, Lem. 3.8] and [14, Thm. 2.5] yields
for \(2 \le p \le \infty \), \(0\le \ell \le k \). We will further make use of the inverse estimates, cf. [8, Thm. 4.5.11] or [30, Lem. 5.6],
for \(1\le p \le q \le \infty \).
For \(u_h\in V_h\) with \(\left\Vert u_h \right\Vert _{L^\infty } \le {\widehat{r}}_\infty \) and \(\left\Vert u_h \right\Vert _{W^{1,N+\delta }} \le r\), we define an inner product for \(\varphi ,\psi \in L^2(\varOmega _h)\) and the corresponding \(L^2\)-projection \(Q_h(u_h) :L^2(\varOmega _h) \rightarrow V_h\) used in (2.8) for \(\psi _h \in V_h\) by
and obtain by the standard techniques for \(p \in [2,\infty ]\) and \(\psi \in L^p, \varphi \in H^1(\varOmega _h)\)
see for example [35] in the case \(p=\infty \). The constants are controlled by the norms of \(u_h\) in \(L^\infty \) and \(W^{1,N+\delta }\).
Finally, we introduce the first-order lift operator \({\varvec{{\mathcal {L}}_h}}:W^{\ell ,p}(\varOmega _h)^2 \rightarrow W^{\ell ,p}(\varOmega )^2\), \(\ell =0,1\), \(2 \le p \le \infty \), the adjoint lift \({\varvec{{\mathcal {L}}_h}}^{*}:X\rightarrow X_h\), and the reference operator \(J_h:V\times V\rightarrow X_h\) defined by
which are bounded uniformly in h due to (2.2), (2.23), and (2.24). From the proof of [20, Lem. 4.7], we then obtain the identity
which is used several times in the proofs.
3 Error Analysis for the Space Discretization
In this section, we give the proof of Theorem 2.5. We decompose the error into
where the projection error \(e_{J_h}\) is easily bounded using (2.24). The first part of the proof consists in reducing the bound on \(\left\Vert e_h \right\Vert _{W^{1,{p^*}}\times H^1}\) to an estimate in the stronger norm induced by \(\left\Vert \textrm{A}_h\cdot \right\Vert _{X_h}\), and not in the standard \(X_h\)-norm.
The second part consists in establishing the stronger norm bound on \(\left\Vert \textrm{A}_he_h \right\Vert _{X_h}\) in Sect. 3.2. We note that a key idea is to set up an appropriate solution space for the numerical approximation, see (3.3), which allows for an appropriate formulation of the error equation. We give a detailed explanation in Remark 3.6.
3.1 Reduction to Stronger Norm Estimates
For \({p^*}\) defined in (2.13), we chose some fixed \(\delta >0\) such that
a radius \(r_\infty < {\widehat{r}}_\infty \) from Assumption 2.1, and another radius \(r'_\infty >0\), such that
where \(\left\Vert x \right\Vert _{L^\infty {(X)}} {:}{=}\max _{[0,T]}\left\Vert x(t) \right\Vert _{X} \). We denote by \(t^*_h\) the time with
We assume for a moment that the set is not empty and hence \(t^*_h>0\), see Proposition 3.5. The following result is a direct consequence of Lemma 2.10 and the key ingredient to ensure wellposedness of the discrete equation. In addition, it enables us to employ energy techniques in the error analysis.
Lemma 3.1
Let Assumption 2.1 hold. We have for \(t \in [0,t^*_h]\), \(1 \le p \le \infty \), and \(j =0,1\) the bounds
with a constant \(C_{\lambda } > 0\) depending only on \(\lambda \), its derivatives and \({\widehat{r}}_\infty , r'_\infty \), but is independent of h and \(t^*_h\).
Proof
We use the definition of \(\lambda _h\) and \(\lambda _h^{-1}\) in (2.6) and (2.8), respectively, to conclude the assertion from Assumption 2.1, the stability in (2.26), the interpolation property (2.22), and (3.3). \(\square \)
Making extensive use of Lemma 3.1, we show via energy techniques in Sect. 3.2 the following error bound on
Note that initially the result is only valid as long as the bounds in (3.3) hold.
Proposition 3.2
Under the assumptions of Theorem 2.5, it holds for \(0\le t \le t^*_h\)
where C is independent of h and \(t^*_h\).
From this bound, we are able to extract convergence as well as to extend the final time \(t^*_h\) beyond T for sufficiently small h. Concerning \(u_h\), we show in the following lemma how to obtain convergence in the maximum norm and first-order Sobolev norms, but postpone the proof to Appendix C. Further, we may directly deduce the bounds on \(u_h\) in (3.3). Note that this lemma can be seen as a discrete analogue to (2.14) and is an improved variant of the results in [7, 13]. Similar bounds were already shown in [18, Thm. 1.12] and [36, Thm. 3].
Lemma 3.3
Let \({p^*}\) be given by (2.13). Then, there is a constant C independent of h such that
for all \(\varphi _h \in V_h\). In the case \(N=3\), the statement also holds for \({p^*}= 6\).
A further ingredient in the proof of the main result is to employ the \(H^1\)-bound on \(v_h\) in Proposition 3.2 to derive boundedness in \(L^\infty \) and \(W^{1,N+\delta }\) and thus extend the final time \(t^*_h\).
Lemma 3.4
Let \(\varphi _h \in V_h\) and \(\varphi \in W^{k+1,\infty }(\varOmega ) \cap V\), and assume that
Then, we have for \({p^*}\) defined in (2.13) and \(\delta \) chosen in (3.1)
with a constant C independent of h.
Since \(k\ge 1\), the choice in (2.13) enables to us to deduce the desired bounds (3.3) in \(L^\infty \) and \(W^{1,N+\delta }\) from approximation properties in \(H^1\) and hence allows us to extend the final time \(t^*_h\).
Proof
(of Lemma 3.4) For \(\psi _h \in V_h\), we combine the inverse estimate (2.25) and the Sobolev embedding \(H^1(\varOmega _h) \hookrightarrow L^{{p^*}}(\varOmega _h)\) and conclude by (3.1)
with a constant C independent of h. For the desired bound, we expand with the adjoint lift \({\mathcal {L}}_h^{V*}\) and obtain by (2.24)
Since \( {\mathcal {L}}_h^{V*}\varphi - \varphi _h \in V_h\), the first assertion then follows from (3.6a) together with (3.5). The second estimate is derived fully analogously. \(\square \)
Hence, once we have shown Proposition 3.2, we can give the proof of our first main result.
Proof
(of Theorem 2.5)
Inserting the adjoint lift, we obtain for \(t\in [0,t^*_h]\) with (2.24), (3.4), and Lemma 3.3 the bound
and similarly
with a constant C independent of h and \(t^*_h\). Hence, it remains to show \(t^*_h= T\). Combining the bounds in Proposition 3.2 and Lemma 3.3, we show by (3.2) for h sufficiently small that
as well as with Proposition 3.2 and Lemma 3.4
Thus, the continuity of the discrete solution \(y_h\) and the equivalence of all norms in finite-dimensional spaces yields \(t^*_h\ge T\). In particular, the statement of Theorem 2.5 is true for \(t\in [0,T]\). \(\square \)
3.2 Proof of Proposition 3.2
The rest of this section is devoted to the proof of Proposition 3.2. The first step is to show that the set defined in (3.3) is not empty.
Proposition 3.5
The initial error satisfies
where C is independent of h. In particular, it holds \(0 < t^*_h\le T\).
Proof
The bound directly follows from the choice (2.12), the interpolation properties in (2.22), and the bounds in Proposition 2.4. To show that \(t^*_h>0\), we proceed as in the proof of Theorem 2.5 with \(t=0\) instead of \(t = t^*_h\). \(\square \)
With the aid of Lemma 3.1, we are able to define with \(\varLambda _h(y_h)\) from (2.7) the state-dependent inner products
The corresponding norm is equivalent to the norm of \(X_h\), i.e., we have
with the constants from Lemma 3.1.
3.3 Error Equation
We study the bound on the discrete error \(e_h\) and derive an evolution equation for it. Inserting the projected solution \(J_hy\) of (2.1) in (2.10), we obtain
with defect
This leads us to the error equation
where the stability term is given by
Remark 3.6
Let us explain the main differences to the error analysis presented by Maier and Hochbruck [21, 31] and Makridakis [32]. In [21, 31], instead of \(\varLambda _h(y_h)\) they use \(\varLambda _h( I_hy)\) which has the properties from Lemma 3.1. However, to bound the stability term, inverse inequalities are used which induce restrictions on the polynomial degree and also the CFL-type condition. Our technique is more related to [32], where bounds on \(\left\Vert u_h \right\Vert _{W^{1,\infty }}\) replace (3.3).
However, in both approaches the error analysis is performed in \(H^1\times L^2\). They thus have to impose stronger CFL-type conditions to close the argument.\(\lozenge \)
We introduce the state-dependent operator
and define the modified error as
Differentiating the term \(\varLambda _h(y_h(t)) {\widetilde{e}}_h(t)\) and using (3.9) lead to the following modified error equation
We state two results on the stability term and the defect and postpone their proofs to Sect. 5.
Lemma 3.7
For \(0\le t\le t^*_h\), it holds
with a constant C independent of h and \(t^*_h\).
Similarly, we show the optimal error bound of the defect in the stronger norm.
Lemma 3.8
For \(0\le t\le t^*_h\) it holds
with a constant C independent of h and \(t^*_h\).
In addition, we note that by (2.7) and Lemma 3.1 there is a constant C independent of h and \(t^*_h\) such that for all \(x_h \in X_h\) it holds
With these two lemmas and the bound on the initial error in Proposition 3.5, we conclude the remaining estimate.
Proof
(of Proposition 3.2) We first compute
Inserting the error equation (3.11), we use the skew-symmetry of \(\textrm{A}_h\) and combine the bounds in (3.12) and Lemmas 3.1, 3.7, and 3.8 to obtain
The application of a Gronwall lemma together with Proposition 3.5 and (3.7) then yields the assertion. \(\square \)
4 Error Analysis for the Full Discretization
We carry over the results and techniques established in the last section to the fully discrete schemes. We work with a discrete analogous of (3.3) given by a final time step \({n^*}\) which allows us to perform the next time step to \(t^{{n^*}+1}\), that is
In particular, we will establish \({n^*}\ge N-1\). Note that by (2.16) formally, we have to show that \({n^*}\ge 1\) for the last term in (4.1), which can be interpreted as providing both the base cases \(n=0,1\) in the induction. However, the case \(n=0\) is already covered by Proposition 3.2, such that the set in (4.1) is not empty, and it holds \({n^*}\ge 0\).
Further, note that similar to Lemma 3.1 we conclude from the bounds in (4.1) that for \(0 \le n \le {n^*}\), \(1 \le p \le \infty \), and \(j =0,1\) it holds
and the bounds in Lemma 3.1 in the \(H^1\)-norm remain valid.
Throughout this section, we employ several times the estimate from Lemma 3.3, and also a straightforward extension of Lemma 3.4 including the temporal convergence rate.
Lemma 4.1
Let \(\varphi _h \in V_h\) and \(\varphi \in W^{k+1,\infty }(\varOmega ) \cap V\), and assume that for some \(\ell \in \{1,2\}\) it holds
Then, we have
with a constant C independent of h and \(\tau \).
4.1 Euler
First note that for the Euler method (2.17), we have by construction \(\partial _{\tau }u_h^{k} = v_h^{k}\) such that it is sufficient to check the first three conditions. As above, we define the discrete error by \(e_h^{n} = J_hy(t^{n}) - y_h^{n}\) and aim to show as in Proposition 3.2 the following bound.
Proposition 4.2
Under the assumptions of Theorem 2.6, for \(0\le n \le {n^*}+ 1\) it holds the bound
where C is independent of h, \(\tau \) and \({n^*}\).
As in the spatially discrete case, this estimate allows us to immediately conclude our main result.
Proof
(of Theorem 2.6) We proceed along the lines of the proof of Theorem 2.5 to conclude the convergence up to \(t^{{n^*}+1}\). In addition, Lemma 3.3 and the CFL-type condition (2.18) together with Lemma 4.1 for \(\ell =1\) further allow us to prove \({n^*}\ge N-1\) for \(h,\tau \) sufficiently small, and the assertion is shown for all n. \(\square \)
The rest of this section is devoted to the proof of Proposition 4.2. In order to derive the error equation, we insert the projected exact solution \(J_hy\) of (2.1) in the scheme (2.17) and derive
with defect \(\delta _{\text {Eu}}^{n+1} = \delta _{h,\text {Eu}}^{n+1} + \delta _{\tau ,\text {Eu}}^{n+1} \) given by
This yields the discrete error equation
where the stability term is given by
In order to obtain a recursion for \(e_h^{n+1}\), we recall the state-dependent operator and define the corresponding resolvent
A simple calculation shows that for the inner product
which satisfies by (4.1) the same bounds as in (3.7), we obtain
and rewrite (4.4) as
Since \( {\textbf{A}}_h^{\hspace{-0.3mm}n}\) commutes with \({\textbf{R}}_{\text {Eu},n}\), we obtain
which has to be resolved. Proceeding as in Lemma 3.7, and noting that for any norm it holds
we have for \(0\le n\le {n^*}\) the stability bound
with a constant C independent of h, \(\tau \) and \({n^*}\). Similarly, we show the optimal consistency error of the defect in the stronger norm, see Sect. 5 for the proof.
Lemma 4.3
For \(0\le n\le {n^*}\), it holds
with a constant C independent of h, \(\tau \) and \({n^*}\).
Hence, we have already established the estimate
and the last step toward the main result is to change the norms.
Lemma 4.4
For \(1\le n\le {n^*}\), it holds for all \(\varphi _h \in V_h\)
with a constant C independent of h, \(\tau \) and \({n^*}\).
Proof
Expanding the norm as
and using (4.2) several times give the assertion. \(\square \)
With this, we are able to proof the estimate on \(\textrm{A}_he_h^{n+1}\).
Proof
(of Proposition 4.2)
We first consider the case \({n^*}= 0\). Hence, (4.8) with \(n=0\) directly yields the assertion without the use of Lemma 4.4 and hence without any bound on \(\partial _{\tau }u_h^{k}\). With this, we established \({n^*}\ge 1\).
In the case \({n^*}\ge 1\), we employ Lemma 4.4 in (4.8) and make use of the norm equivalences to obtain
Resolving the recursion and using Proposition 3.5 yields the result. \(\square \)
4.2 Midpoint
The proof is very similar to the Euler method and hence, we only sketch the relevant details. First note that by construction in (2.19) it holds
such that the last bound in (4.1) does not have to be shown separately. Again, we aim at the following bound.
Proposition 4.5
Under the assumptions of Theorem 2.7, for \(0\le n \le {n^*}+ 1\) it holds the bound
where C is independent of h, \(\tau \) and \({n^*}\).
Combining Lemma 4.1 with the weaker CFL-type condition (2.20) yields the convergence result.
Proof
(of Theorem 2.7) As in the proof of Theorem 2.6, the convergence follows directly. To show that \({n^*}\ge N-1\), we employ Lemma 4.1 with \(\ell =2\) together with the CFL-type condition (2.20). \(\square \)
Hence, it remains to show Proposition 4.5. As for the Euler method, we derive the following error equation
with a stability term similar to the one in (4.5) satisfying
and a composed defect \(\delta _{\text {M}}^{n+1} = \delta _{h,\text {M}}^{n+1} + \delta _{\tau ,\text {M}}^{n+1}\). The first component is basically the same as \(\delta _{h,\text {Eu}}^{n+1}\) in (4.3b), and the second satisfies
such that we derive in Sect. 5 the desired order of convergence.
Lemma 4.6
For \(0\le n\le {n^*}\), it holds
with a constant C independent of h, \(\tau \) and \({n^*}\).
We solve for \(e_h^{n+1}\) in the error equation (4.9) and define for the solution-dependent operator \({\textbf{A}}_h^{\hspace{-0.3mm}n+1/2} = \varLambda _h^{-1}({\bar{y}}^{n + 1/2} ) \textrm{A}_h\) the maps
A simple calculation shows that for the inner product
we have
Rewriting (4.9) and multiplying by \({\textbf{A}}_h^{\hspace{-0.3mm}n+1/2}\), we obtain
Finally, we have as in Lemma 4.4 the following bound when changing the norm.
Lemma 4.7
For \(1\le n\le {n^*}\) it holds
with a constant C independent of h, \(\tau \) and \({n^*}\).
Proof
First note that
as well as
This allows us to proceed as in Lemma 4.4 and to bound \(\partial _{\tau }^j \varLambda _h({\bar{y}}^{n + 1/2} )\), \(j=0,1\), and the inverse \(\varLambda _h^{-1}({\bar{y}}^{n + 1/2} )\). \(\square \)
We are then able to conclude the error bound for the midpoint rule.
Proof
(of Proposition 4.5) Using the error equation (4.12), we employ Lemmas 4.6 and 4.7, and (4.10) to obtain
With the bound on \(\textrm{A}_he_h^{0}\) from Proposition 3.5 and using the fact the first step is given by the Euler method, we obtain with Proposition 4.2
which yields by a Gronwall lemma the assertion. \(\square \)
4.3 Exponential Euler
For the exponential method, we apply a similar approach and derive the necessary bound in the stronger energy norm. However, there is no direct relation to the discrete derivatives of the error. In this case, we have to prove an additional error estimate.
Proposition 4.8
Under the assumptions of Theorem 2.8, for \(0\le n \le {n^*}+ 1\) there hold the bounds
and for \(1\le n \le {n^*}+ 1\)
where C is independent of h, \(\tau \), and \({n^*}\).
Once this is established, the last main result directly follows.
Proof
(of Theorem 2.8) In order to conclude the convergence rates, we only employ the first estimate in Proposition 4.8. To show \({n^*}\ge N-1\), again the first estimate allows us to guarantee the first three bounds in (4.1). The bound on \({\mathcal {L}}_h\partial _{\tau }u_h^{k}\) follows from the second estimate in Proposition 4.8 combined with Lemma 4.1 and the CFL-type condition (2.18). \(\square \)
The rest of this section is devoted to the proof of Proposition 4.8. We introduce the auxiliary approximation \({\tilde{y}}^{n}(t^{n} + s)\) for \(s\in [0,\tau ]\) as the solution of
and thus satisfies \({\tilde{y}}^{n}(t^{n} + \tau ) = y_h^{n+1}\). In order to derive the error equation, we insert the projected exact solution \(J_hy\) in (4.13)
with defect \(\delta _{\text {ExEu}}^{n+1} = \delta _{h,\text {ExEu}}^{n+1} + \delta _{\tau ,\text {ExEu}}^{n+1} \) given by
Similarly, we define the auxiliary error by
This yields the discrete error equation for \(s\in [0,\tau ]\)
with stability term
Using the variation-of-constants formula with the state-dependent operator defined in (4.6), we obtain from (4.14)
To obtain the error bounds stated in Proposition 4.8, we need the following two estimates which follow along the lines of Lemmas 3.7 and 4.3: For \(0\le n \le {n^*}\) it holds
with a constant C independent of h, \(\tau \) and \({n^*}\). This allows us to conclude the bounds in the two stronger norms.
Proof
(of Proposition 4.8) We proceed as in the proof of Proposition 4.2 in order to obtain the bound on \(\textrm{A}_h{\tilde{e}}_h^{n}\) in the form
which implies the first statement in the proposition. For the discrete derivative of the error, we employ (4.7), (4.14), and (4.15) to conclude
where we used (4.16) in the last step. \(\square \)
4.4 Exponential Midpoint Rule
For the exponential midpoint rule, we combine the approaches presented for the semi-implicit midpoint rule and the exponential Euler method. In particular, we have to prove error bounds in the stronger norm as well as for the discrete derivative of the error.
Proposition 4.9
Under the assumptions of Theorem 2.9, for \(0\le n \le {n^*}+ 1\), there hold the bounds
and for \(1\le n \le {n^*}+ 1\)
where C is independent of h, \(\tau \) and \({n^*}\).
Once this is established, the last main result directly follows.
Proof
(of Theorem 2.9) We only combine the argument presented in the proofs of Theorems 2.7 and 2.8 to conclude the assertion. \(\square \)
The rest of this section is devoted to the proof of Proposition 4.9. We introduce the auxiliary approximation \({\tilde{y}}^{n}(t^{n} + s)\) for \(s\in [0,\tau ]\) as the solution of
with \({\tilde{y}}^{n}(t^{n}) =y_h^{n}\), and thus satisfies \({\tilde{y}}^{n}(t^{n} + \tau ) = y_h^{n+1}\). In order to derive the error equation, we insert the projected exact solution \(J_hy\) in (4.17) and conclude
with defect \(\delta _{\text {ExM}}^{n+1} = \delta _{h,\text {ExM}}^{n+1} + \delta _{\tau ,\text {ExM},1}^{n+1} + \delta _{\tau ,\text {ExM},2}^{n+1} \) given by
Deriving the error equation and using the variation-of-constants formula, we obtain with the state-dependent operator \({\textbf{A}}_h^{\hspace{-0.3mm}n+1/2} = \varLambda _h^{-1}({\bar{y}}_h^{n + 1/2} ) \textrm{A}_h\)
with stability term
Unlike for the exponential Euler method, one has to pay more attention to the derivation of the error bound on the discrete derivatives. In order to show the error bound, we do not only apply \( {\textbf{A}}_h^{\hspace{-0.3mm}n+1/2}\) to the error equation, but also apply the discrete derivative \(\partial _{\tau }\). In a straightforward manner, one can derive the following auxiliary result.
Lemma 4.10
Under the assumptions of Theorem 2.9, it holds for \(0\le \sigma \le \tau \)
with a constant C independent of h, \(\tau \) and \({n^*}\).
This leads to several error terms which appeared above similarly. Along the lines of Lemmas 3.7, 4.3 and 4.6, we immediately conclude the following bounds: For \(0\le n \le {n^*}\), the stability terms are bounded by
and further the defects satisfy
with a constant C independent of h, \(\tau \) and \({n^*}\). The main difficulty is to extract the additional order of convergence in the defect \(\delta _{\tau ,\text {ExM},2}^{n}\). We show in Sect. 5 the following lemma.
Lemma 4.11
Under the assumptions of Theorem 2.9, it holds
with a constant C independent of h, \(\tau \), and \({n^*}\).
From this, we conclude the error bounds in Proposition 4.9.
Proof
(of Proposition 4.9) Following the lines of the preceding proofs of Propositions 4.5 and 4.8, one establishes the error bound on \(\left\Vert \textrm{A}_he_h^{n} \right\Vert _{X_h}\). Applying the discrete derivative to the error equation and employing the bounds in Lemma 4.10 combined with (4.18) and (4.19) yield
where the remainder term \(\varDelta _h^n\) satisfies
Finally, the application of Lemma 4.11 yields the desired estimate on \(\left\Vert \partial _{\tau }e_h^{n} \right\Vert _{X_h}\) and closes the proof. \(\square \)
5 Estimates for Stability Terms and Defects
This section is devoted to the proofs of the postponed stability and consistency estimate from Sects. 3 and 4.
5.1 Stability
In the following, we give a detailed proof for the stability term given in (3.10). We emphasize that the corresponding bounds used in Sect. 4 are derived fully analogously, and we thus refrain from giving the details here.
Proof
(of Lemma 3.7) We consider the two contributions of \(\varGamma _h\) in (3.10) separately.
(a) We first note by (2.6) and (2.7) that
Without loss of generality, we show the assertion only for \(g(t, u, \partial _tu) = g(\partial _tu)\) and obtain
where we used Lemma 2.10 for the last estimate. The latter term is estimated with (3.4) by \(\textrm{A}_he_h\) in the \(X_h\)-norm. For the integral part, we use the stability of \({\mathcal {L}}_h{\mathcal {L}}_h^{V*}\) in (2.24) with \(\ell =0\) to bound it by a constant depending on the \(W^{1,N+\delta }\)-norms of \(\partial _tu\) and \(v_h\). Hence, the bounds in (3.3) yield the stability for \(G_h\).
(b) Next, we consider by (2.6) and (2.7)
and estimate with the stability of the \(L^2\)-projection in (2.26) and of the interpolation (2.22), the algebra property of \(W^{1,N+\delta }\), and the stability of \({\mathcal {L}}_h^{V*}\) in (2.24)
with a constant depending on the \(W^{1,N+\delta }\)-norms of \(u\) and \(u_h\). Using Lemma 3.3 and (3.4), the first term is bounded by \(\textrm{A}_he_h\) in the \(X_h\)-norm. \(\square \)
5.2 Defects
We first estimate the spatial defect (3.8) which will reappear in a modified form in the defects of the full discretization.
Proof
(of Lemma 3.8)
-
(a)
We compute with (2.27) and (2.28)
$$\begin{aligned} \textrm{A}_h\bigl (J_h\textrm{A}- \textrm{A}_hJ_h\bigr ) y(t) = \textrm{A}_h\bigl (J_h- {\varvec{{\mathcal {L}}_h}}^{*}\bigr )\textrm{A}y(t) = \begin{pmatrix} ( {\mathcal {L}}_h^{V*}- {\mathcal {L}}_h^{H*}) \mathrm {\Delta }u\\ 0 \end{pmatrix} \end{aligned}$$and, inserting the interpolation, estimate with (2.22), (2.23), (2.24), and (2.25),
$$\begin{aligned} \left\Vert \textrm{A}_h\bigl (J_h\textrm{A}- \textrm{A}_hJ_h\bigr ) y(t) \right\Vert _{X_h} \le C h^k \left\Vert \mathrm {\Delta }u \right\Vert _{H^{k+1}}. \end{aligned}$$ -
(b)
As above, we only consider the case \(g(t, u, \partial _tu) = g(\partial _tu)\) and obtain with (2.6) and (2.7)
$$\begin{aligned} \textrm{A}_h\bigl ( J_hG(t, y) - G_h(t, J_hy) \bigr ) = \begin{pmatrix} {\mathcal {L}}_h^{V*}g(\partial _tu) - I_hg({\mathcal {L}}_h{\mathcal {L}}_h^{V*}\partial _tu) \\ 0 \end{pmatrix}. \end{aligned}$$From this, we conclude with (2.22) and (2.24)
$$\begin{aligned}&\left\Vert \textrm{A}_h\bigl ( J_hG(t, y) - G_h(t, J_hy) \bigr ) \right\Vert _{X_h} \\&\quad \le \bigl \Vert ({\mathcal {L}}_h^{V*}- I_h) g( \partial _tu) \bigr \Vert _{V_h} + \bigl \Vert I_hg(\partial _tu) - I_hg({\mathcal {L}}_h{\mathcal {L}}_h^{V*}\partial _tu) \bigr \Vert _{V_h} \\&\quad \le \,C h^k \left\Vert g( \partial _tu) \right\Vert _{H^{k+1}} + C \bigl \Vert (\textrm{Id}-{\mathcal {L}}_h{\mathcal {L}}_h^{V*}) \partial _tu \bigr \Vert _{W^{1,\infty }} \\&\quad \le \,C ( \left\Vert g( \partial _tu) \right\Vert _{H^{k+1}} + \left\Vert \partial _tu \right\Vert _{W^{k+1,\infty }} ) \, h^k , \end{aligned}$$which gives the desired convergence rate.
-
(c)
We compute with (2.6) and (2.7)
$$\begin{aligned} \textrm{A}_h\bigl ( J_h\varLambda (y) \! -\! \varLambda _h(J_hy) J_h\bigr ) \partial _ty\!\! =\!\!\begin{pmatrix} {\mathcal {L}}_h^{V*}( \lambda (u) \partial _t^2 u)\! -\! \pi _h\bigl ( I_h\lambda ({\mathcal {L}}_h{\mathcal {L}}_h^{V*}u) {\mathcal {L}}_h{\mathcal {L}}_h^{V*}\partial _t^2 u\bigr ) \\ 0 \end{pmatrix}, \end{aligned}$$such that again (2.22), (2.23) and (2.24) yield the estimate
$$\begin{aligned}&\left\Vert \textrm{A}_h\bigl ( J_h\varLambda (y) - \varLambda _h(J_hy) J_h\bigr ) \partial _ty \right\Vert _{X_h} \\&\quad \le \bigl \Vert ({\mathcal {L}}_h^{V*}- {\mathcal {L}}_h^{H*}) \lambda (u) \partial _t^2 u \bigr \Vert _{V_h} + \bigl \Vert ({\mathcal {L}}_h^{H*}- \pi _h{\mathcal {L}}_h^{-1}) \lambda (u) \partial _t^2 u \bigr \Vert _{V_h} \\&\qquad + \bigl \Vert \lambda (u) \partial _t^2 u- {\mathcal {L}}_hI_h\lambda ({\mathcal {L}}_h{\mathcal {L}}_h^{V*}u) {\mathcal {L}}_h{\mathcal {L}}_h^{V*}\partial _t^2 u \bigr \Vert _{V_h} \\&\quad \le \,C (\left\Vert \lambda ( u) \right\Vert _{W^{k+1,\infty }} , \bigl \Vert \partial _t^2u \bigr \Vert _{W^{k+1,\infty }} ) \, h^k + h^{-1} \bigl \Vert ({\mathcal {L}}_h^{H*}- \pi _h{\mathcal {L}}_h^{-1}) \lambda (u) \partial _t^2 u \bigr \Vert _{H_h}. \end{aligned}$$
The last term is estimated using [16, Lem. 8.24] to obtain
and (2.22) together with (B.2) gives the desired bound. \(\square \)
For the fully discrete defects, we rely on further Lipschitz bounds of the nonlinearities \(\varLambda \) and \(G\) which we collect in the next lemma. Since we work in a first-order framework, we denote in the following for any function \(x \in X\), the projection onto the first and second component by \(x_1\) or \(x_2\), respectively.
Lemma 5.1
Let \(x,y,z \in X\), and let Assumption 2.1 hold.
-
(a)
If \(x_1,y_1,z_2 \in W^{1,\infty }(\varOmega )\), then
$$\begin{aligned} \left\Vert \textrm{A}\bigl ( \varLambda ( x ) - \varLambda ( y ) \bigr ) z \right\Vert _{X} \le C \left\Vert x_1 - y_1 \right\Vert _{H^1(\varOmega )} , \end{aligned}$$where the constant depends on the \(W^{1,\infty }\)-norms of \(x_1,y_1,z_2\).
-
(b)
If \(x_1,x_2,y_1,y_2 \in W^{1,\infty }(\varOmega )\), then
$$\begin{aligned} \left\Vert \textrm{A}\bigl ( G(t, x ) - G(s, y ) \bigr ) \right\Vert _{X} \le C \bigl ( |t-s| + \left\Vert x_1 - y_1 \right\Vert _{H^1(\varOmega )} + \left\Vert x_2 - y_2 \right\Vert _{H^1(\varOmega )} \bigr ) \end{aligned}$$where the constant depends on the \(W^{1,\infty }\)-norms of \(x_1,x_2,y_1,y_2\).
Proof
We expand the difference in part (a) as
and the assumptions in the lemma yield the bound. The very same computation yields the second estimate (b). \(\square \)
Thus, the defect of the Euler method can be bounded in a straightforward way.
Proof
(of Lemma 4.3) We recall the splitting \(\delta _{\text {Eu}}^{n+1} = \delta _{h,\text {Eu}}^{n+1} + \delta _{\tau ,\text {Eu}}^{n+1} \) of the defect in (4.3), and note that by proof of Lemma 3.8 it holds
We treat the two parts in (4.3b) separately. The second term involving \(G\) is bounded using (2.28) and Lemma 5.1. Further, we expand
such that Lemma 5.1 is employed on the first part. For the second part, note that by the fundamental theorem of calculus we obtain in any norm
and the claim follows. \(\square \)
Similarly, we bound the defect of the midpoint rule in (4.11), and as above we do not have to treat the spatial part \(\delta _{h,\text {M}}^{n+1}\).
Proof
(of Lemma 4.6) We first note that from Taylor expansions and the Peano kernel theorem, we conclude in any norm the bounds
Combining this with Lemma 5.1 and the proof of Lemma 4.3 yields the desired bounds on the defect. \(\square \)
We finally treat the principle defect of the exponential midpoint rule. We pursue the strategy adapted from [12, Prop. 5.3]. Before we give the proof, we need two auxiliary results. The first one allows us to compare function evaluations of finite element objects with their interpolation. The proof is given in Appendix B.
Lemma 5.2
Let \(L \in {\mathbb {N}}\) and assume that \(f :{\mathbb {R}}^L \rightarrow {\mathbb {R}}\) is sufficiently often differentiable and that \(\varphi _{i,h} \in V_h\) satisfies
for \(i = 1, \ldots . L\). Then,
with a constant independent of h.
On the continuous level, the chain rule allows us to bound terms of the form \(\mathrm {\Delta }(\mu (u) w )\) by the norms of \(\mathrm {\Delta }u\) and \(\mathrm {\Delta }w\). Even though this is not straightforward in the discrete case, one can establish a very similar result. We recall the Ritz projection \(R_h\) defined in (2.5) and note that the proof is given in Appendix D.
Lemma 5.3
Let \(u_h, w_h \in V_h\) and assume that \(\left\Vert \mathrm {\Delta }_hu_h \right\Vert _{L^2} + \left\Vert \mathrm {\Delta }_hw_h \right\Vert _{L^2} \le C\). Further, let \(\mu :{\mathbb {R}}\rightarrow {\mathbb {R}}\) be twice continuously differentiable. Then,
with a constant C independent of h.
With these preparations, we can provide the error bounds on the defects of the exponential midpoint rule.
Proof
(of Lemma 4.11) Let us denote
then it remains to show for \(i=1,2\)
Following the lines of the proof of [12, Prop. 5.3], we observe that for the first bound on \(d_n^1\), we have to establish the bounds
as well as for \(d_n^2\) the bounds
For the discrete derivative, we have similar terms which have one \(\textrm{A}_h\) less, and instead \(\partial _{\tau }\) applied to objects following \(\varLambda _h^{-1}({\bar{y}}_h^{n + 1/2})\). In the following, we only discuss the bounds in (5.1a) and (5.2a) since the remaining ones are more standard.
Denoting \(w_h {:}{=}{\mathcal {L}}_h^{V*}\bigl ( \lambda '(u) \, \partial _tu\, \partial _t^2 u\bigr )\), it is sufficient to show for the bound in (5.1a) the estimate
since the first component vanishes. In the following, we will often use that by (2.28) and the assumptions of Theorem 2.9 it holds
and to keep the notation simple, we will write \(u_h\) instead of \({\bar{u}}_h^{n + 1/2}\). We split the term using the inverse estimate in the form (A.1) in
The first term is bounded by Lemma 5.3 using
To split the second term further, we add and subtract in the second term \( Q_h\bigl ( \lambda (u_h)^{-1} w_h \bigr )\), and obtain for the first term with the \(L^2\)-stability of \(Q_h\) in (2.26) and the inverse estimate (2.25)
where we used in the last step Lemma 3.3, the identity
and the maximum norm estimate on \(u_h\). Finally, Lemma 5.2 leads to a uniform bound in h. Using the identity
the assertion follows, once we have established
However, applying Lemma 5.2 once more gives precisely this estimate. The bound in (5.2a) is derived in the very same way. \(\square \)
References
Antonietti, P.F., Mazzieri, I., Muhr, M., Nikolić, V., Wohlmuth, B.: A high-order discontinuous Galerkin method for nonlinear sound waves. J. Comput. Phys. 415, 109,484, 27 (2020), https://doi.org/10.1016/j.jcp.2020.109484
Arndt, D., Bangerth, W., Feder, M., Fehling, M., Gassmöller, R., Heister, T., Heltai, L., Kronbichler, M., Maier, M., Munch, P., Pelteret, J.P., Sticko, S., Turcksin, B., Wells, D.: The deal.II library, version 9.4. J. Numer. Math. 30(3), 231–246 (2022), https://dealii.org/deal94-preprint.pdf
Bales, L.A.: Higher-order single-step fully discrete approximations for nonlinear second-order hyperbolic equations. pp. 581–604 (1986). Hyperbolic partial differential equations, III
Bales, L.A.: Error estimates for single step fully discrete approximations for nonlinear second order hyperbolic equations. pp. 535–553 (1988), https://doi.org/10.1016/0898-1221(88)90279-9. Hyperbolic partial differential equations. V
Bales, L.A., Dougalis, V.A.: Cosine methods for nonlinear second-order hyperbolic equations. Math. Comp. 52(186), 299–319, S15–S33 (1989), https://doi.org/10.2307/2008469
Bangerth, W., Hartmann, R., Kanschat, G.: deal.II—a general-purpose object-oriented finite element library. ACM Trans. Math. Software 33(4), Art. 24, 27 (2007), https://doi.org/10.1145/1268776.1268779
Bramble, J.H., Schatz, A.H., Thomée, V., Wahlbin, L.B.: Some convergence estimates for semidiscrete Galerkin type approximations for parabolic equations. SIAM J. Numer. Anal. 14(2), 218–241 (1977), https://doi.org/10.1137/0714015
Brenner, S.C., Scott, L.R.: The mathematical theory of finite element methods, Texts in Applied Mathematics, vol. 15, third edn. Springer, New York (2008), https://doi.org/10.1007/978-0-387-75934-0
Ciarlet, P.G.: The finite element method for elliptic problems. Studies in Mathematics and its Applications, Vol. 4. North-Holland Publishing Co., Amsterdam-New York-Oxford (1978)
Crandall, M.G., Souganidis, P.E.: Convergence of difference approximations of quasilinear evolution equations. Nonlinear Anal. 10(5), 425–445 (1986), https://doi.org/10.1016/0362-546X(86)90049-0
Dörfler, W., Gerner, H., Schnaubelt, R.: Local well-posedness of a quasilinear wave equation. Appl. Anal. 95(9), 2110–2123 (2016), https://doi.org/10.1080/00036811.2015.1089236
Dörich, B., Hochbruck, M.: Exponential integrators for quasilinear wave-type equations. SIAM J. Numer. Anal. 60(3), 1472–1493 (2022), https://doi.org/10.1137/21M1410579
Dörich, B., Leibold, J., Maier, B.: Maximum norm error bounds for the full discretization of nonautonomous wave equations. IMA J. Numer. Anal. (2023), https://doi.org/10.1093/imanum/drad065
Dörich, B., Leibold, J., Maier, B.: Optimal \(W^{1,\infty }\)-estimates for an isoparametric finite element discretization of elliptic boundary value problems. Electron. Trans. Numer. Anal. 58, 1–21 (2023), https://doi.org/10.1553/etna_vol58s1
Elliott, C.M., Ranner, T.: Finite element analysis for a coupled bulk-surface partial differential equation. IMA J. Numer. Anal. 33(2), 377–402 (2013), https://doi.org/10.1093/imanum/drs022
Elliott, C.M., Ranner, T.: A unified theory for continuous-in-time evolving finite element space approximations to partial differential equations in evolving domains. IMA J. Numer. Anal. 41(3), 1696–1845 (2021), https://doi.org/10.1093/imanum/draa062
Ewing, R.E.: On efficient time-stepping methods for nonlinear partial differential equations. Comput. Math. Appl. 6(1, Issu), 1–13 (1980), https://doi.org/10.1016/0898-1221(80)90055-3
Fujita, H., Saito, N., Suzuki, T.: Operator theory and numerical methods, Studies in Mathematics and its Applications, vol. 30. North-Holland Publishing Co., Amsterdam (2001)
Gauckler, L., Lu, J., Marzuola, J.L., Rousset, F., Schratz, K.: Trigonometric integrators for quasilinear wave equations. Math. Comp. 88(316), 717–749 (2019), https://doi.org/10.1090/mcom/3339
Hipp, D., Hochbruck, M., Stohrer, C.: Unified error analysis for nonconforming space discretizations of wave-type equations. IMA J. Numer. Anal. 39(3), 1206–1245 (2019), https://doi.org/10.1093/imanum/dry036
Hochbruck, M., Maier, B.: Error analysis for space discretizations of quasilinear wave-type equations. IMA J. Numer. Anal. 42(3), 1963–1990 (2022), https://doi.org/10.1093/imanum/drab073
Hochbruck, M., Pažur, T.: Error analysis of implicit Euler methods for quasilinear hyperbolic evolution equations. Numer. Math. 135(2), 547–569 (2017), https://doi.org/10.1007/s00211-016-0810-5
Hochbruck, M., Pažur, T., Schnaubelt, R.: Error analysis of implicit Runge-Kutta methods for quasilinear hyperbolic evolution equations. Numer. Math. 138(3), 557–579 (2018), https://doi.org/10.1007/s00211-017-0914-6
Kanda, S.: Convergence of difference approximations and nonlinear semigroups. Proc. Amer. Math. Soc. 108(3), 741–748 (1990), https://doi.org/10.2307/2047796
Kato, T.: Quasi-linear equations of evolution, with applications to partial differential equations. In: Spectral theory and differential equations (Proc. Sympos., Dundee, 1974; dedicated to Konrad Jörgens), pp. 25–70. Lecture Notes in Math., Vol. 448 (1975)
Kato, T.: Abstract differential equations and nonlinear mixed problems. Lezioni Fermiane. [Fermi Lectures]. Scuola Normale Superiore, Pisa; Accademia Nazionale dei Lincei, Rome (1985)
Kobayashi, Y.: Difference approximation of Cauchy problems for quasi-dissipative operators and generation of nonlinear semigroups. J. Math. Soc. Japan 27(4), 640–665 (1975), https://doi.org/10.2969/jmsj/02740640
Kovács, B., Lubich, C.: Stability and convergence of time discretizations of quasi-linear evolution equations of Kato type. Numer. Math. 138(2), 365–388 (2018), https://doi.org/10.1007/s00211-017-0909-3
Leibold, J.: A unified error analysis for the numerical solution of nonlinear wave-type equations with application to kinetic boundary conditions. Ph.D. thesis, Karlsruher Institut für Technologie (KIT) (2021). https://doi.org/10.5445/IR/1000130222
Maier, B.: Error analysis for space and time discretizations of quasilinear wave-type equations. Ph.D. thesis, Karlsruhe Institute of Technology (2020), https://doi.org/10.5445/IR/1000120935
Maier, B.: Error analysis for full discretizations of quasilinear wave-type equations with two variants of the implicit midpoint rule. IMA J. Numer. Anal. 43(2), 1149–1180 (2023), https://doi.org/10.1093/imanum/drac010
Makridakis, C.G.: Finite element approximations of nonlinear elastic waves. Math. Comp. 61(204), 569–594 (1993), https://doi.org/10.2307/2153241
Meliani, M., Nikolić, V.: Mixed approximation of nonlinear acoustic equations: Well-posedness and a priori error analysis (2022), arXiv:2209.02737
Nikolić, V., Wohlmuth, B.: A priori error estimates for the finite element approximation of Westervelt’s quasi-linear acoustic wave equation. SIAM J. Numer. Anal. 57(4), 1897–1918 (2019), https://doi.org/10.1137/19M1240873
Nitsche, J.A.: \(L_{\infty }\)-convergence of finite element approximation. In: Journées “Éléments Finis” (Rennes, 1975), p. 18. Univ. Rennes, Rennes (1975)
Suzuki, T., Fujita, H.: A remark on the \(L^\infty \) bounds of the Ritz operator associated with a finite element approximation. Numer. Math. 49(5), 529–544 (1986), https://doi.org/10.1007/BF01389704
Takahashi, T.: Convergence of difference approximation of nonlinear evolution equations and generation of semigroups. J. Math. Soc. Japan 28(1), 96–113 (1976), https://doi.org/10.2969/jmsj/02810096
Acknowledgements
The author thanks Selina Burkhard and Constantin Carle for their careful reading of this manuscript. Further, we like to thank Malik Scheifinger for providing us the codes for the numerical experiments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Arieh Iserles.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) - Project-ID 258734477 - SFB 1173.
Appendices
Appendix A: Modified Ritz Map
In this section, we discuss the approximation property of \({\widetilde{R}}_h\) as well as its computation. Note that the same reasoning is valid in the conforming case.
Proof
(of Proposition 2.4) We use the definitions in (2.4b) and (2.11) to compute
We employ the stability of the lift in (2.2) and the interpolation property in (2.22) to obtain
The geometric estimate in [16, Lem. 8.24] together with (2.2) allows us to bound
and the claim follows setting \(k' = k+1\). Further, we use the definition of \(\mathrm {\Delta }_h\) in (2.9) and the inverse estimate (2.25)
and obtain the second bound with one power less in h. \(\square \)
In order to compute (2.11), we have to solve a linear system with the stiffness matrix corresponding to the bilinear form \(\left( \cdot \mid \cdot \right) _{V_h}\) and right-hand side \({\widetilde{\ell }}_{u}\). For a basis \(\varphi _i\), \(i=1,\ldots ,L\), of \(V_h\), the entries are given by
Going through the construction explained in [15, Sec. 4.1.2-\(-\)4.2], one observes that \({\widetilde{\varphi }}_i {:}{=}{\widetilde{{\mathcal {L}}_h}}^{-1} {\mathcal {L}}_h\varphi _i \in {\widetilde{V}}_h\); however, \({\widetilde{\varphi }}_i\) is not a nodal basis function. Since also \({\widetilde{I_h}} u\in {\widetilde{V}}_h\), one only needs to modify the routines which are used to assemble the stiffness matrix corresponding to \(\left( \cdot \mid \cdot \right) _{{\widetilde{V}}_h}\). In particular, denoting for the reference element \({\widehat{K}}\) by \({\widehat{\varphi }}_i\) and \({\widehat{\psi }}_j\) the nodal basis polynomials of \({\mathcal {P}}^k({\widehat{K}})\) and \({\mathcal {P}}^{k'}({\widehat{K}})\), respectively, one is left to compute the inner products
Then, the transformation maps to the elements in \({\widetilde{\varOmega }}_h\) are used to assemble the right-hand side \({\widetilde{\ell }}_{u}\).
Appendix B: Interpolation and Adjoint Lift
In appendix, we provide the proof of Lemma 2.10, (2.23), and Lemma 5.2. The following estimate appears to be standard, but since we could not find a reference in the literature, we provide its proof here.
Lemma B.1
For \(m=0,1\), there is a constant \(C_{m}>0\) independent of h such that
for all \(\varphi _h,\psi _h \in V_h\).
Proof
Writing \({\mathcal {L}}_hI_h= \textrm{Id}+ ({\mathcal {L}}_hI_h- \textrm{Id})\), by (2.2) it is sufficient to show the assertion for \({\mathcal {L}}_hI_h- \textrm{Id}\) instead of \(I_h\). Passing to the reference cell \({\widehat{K}}\), we only consider the case \(m=1\). We define the map
which is a bounded linear operator with a constant C, such that for any \(\varphi \in {\mathcal {P}}_{2 k}({\widehat{K}})\)
Then, employing [16, Lem. 4.12] yields the result on an arbitrary cell K. \(\square \)
With this, we directly conclude the desired stability estimate.
Proof
(of Lemma 2.10) By the nodal interpolation property (2.3) and Lemma B.1, we obtain
Using Sobolev’s embedding and the stability of the interpolation from (2.22), we further estimate
By the same reasoning, we obtain the bound in the \(L^2\)-norm. \(\square \)
Proof
(of (2.23))
The stability of \({\mathcal {L}}_h^{H*}\) directly follows from the definition (2.4) and the stability of the lift \({\mathcal {L}}_h\) in (2.2). For the error bound, we first observe
For the first term we apply (2.22), and for the difference we use [16, Lem. 8.24] to obtain
with the boundary layer \(U_h {:}{=}\{ x \in \varOmega \mid {\text {dist}}(x,\partial \varOmega ) \le h\}\). Below, we show
and use this together with \(\text {vol}(U_h)^{1/2} \lesssim h^{1/2}\) to estimate
where we used the inverse inequality (2.25) in the last step. The stability of the interpolation (2.22) and the Sobolev embedding yield
and thus the assertion. To show (B.1), we pick some \(x_0 \in U_h\) and \(y_0 \in \partial \varOmega \) with \(|x_0 -y_0 | \le h\) such that
Then, we use the fundamental theorem of calculus to see
which gives the assertion. \(\square \)
For the interpolation estimate in Lemma 5.2, we exploit that the \((k+1)\)-st derivative vanishes for polynomials of degree k. With this one can gain an additional power of h, but does not have to apply an inverse estimate to the highest derivative. In a different context, this was also used by Nitsche in [35, p. 7].
Proof
(of Lemma 5.2) We perform the proof in the case \(L=2\), and explain the generalization in the end. Thus, consider \(\varphi _h,\psi _h \in V_h\) satisfying the assumptions of the lemma. We expand the expression over all elements, which gives
as well as
In the following, we show on each element K
which, by summing over all K, gives the assertion by the Cauchy–Schwarz inequality
The constant C depends on the maximum norm of \(\varphi _h\) and \(\psi _h\) and is thus uniformly bounded by assumption.
If we denote by \({\widehat{K}}\) the reference element, and denote by \(A_K\) the affine part of the element maps, we know from [16, Lem. 4.12] that
On the other hand, by the same lemma [16, Lem. 4.12] it holds
We now treat the summands separately and show
for \(r=0,\ldots , k+1\), which then implies our claim. In the case \(r=0\), we directly obtain
and (B.3) follows.
For \(r \ge 1\), we use the inverse estimate on the reference element in the forms
differentiate the term \(f({\widehat{\varphi }}_h,{\widehat{\psi }}_h)\), and reduce all derivatives by the inverse estimate to \(\nabla {\widehat{\varphi }}_h\). Then, using the maximum norm bound on \({\widehat{\varphi }}_h\) and \({\widehat{\psi }}_h\), we obtain
Note that for \(r=1\), the quadratic term can be dropped. For \(r \le k\), we employ the inverse estimate once more, to obtain with \(k-(r+1) \ge - 1\)
and (B.3) also follows for \(1\le r\le k\).
For \(r=k+1\), we exploit that \(\partial ^{k+1} {\widehat{\varphi }}_h = 0\), and thus, (B.4) yields
This gives the claim of the lemma in the case \(L=2\).
In order to treat \(L>2\), we only need a modification of (B.4) since nothing changes for \(r=0\). A straightforward computation gives
and the same ideas apply. \(\square \)
Appendix C: Discrete Sobolev embedding
The proof is adapted from the conforming case presented in [7, Lem. 4.1], but is able to cover a larger range of exponents. Similar results including the discrete differential operator \(\mathrm {\Delta }_h\) are shown in [18, Thm. 1.12] and [36, Thm. 3].
Proof
(of Lemma 3.3)
First, we define the inverse \(S_h\) of \(\mathrm {\Delta }_h\) form (2.9) by
and its continuous counterpart \(S= \varDelta ^{-1}\) satisfying
We further define the modified solution operator \({\widetilde{S}}_h= {\mathcal {L}}_h^{V*}S{\mathcal {L}}_h\) and write \(S_h= {\widetilde{S}}_h+ (S_h- {\widetilde{S}}_h)\). For the first term, we use the stability of the Ritz map in \(W^{1,{p^*}}\) from (2.24) with \(\ell = 0 \) and (2.14) to obtain
It remains to bound the difference, stemming from the nonconformity, by the inverse estimate (2.25)
We use [16, Lem. 8.24] to obtain
which yields
and hence the assertion. \(\square \)
D Chain Rule for the Discrete Differential Operator
In this section, we provide the proof of Lemma 5.3. We recall the Ritz projection defined in (2.5) and first show a crucial bound in \(L^2\).
Lemma D.1
Let \(u_h, \varphi _h \in V_h\) and assume that \(\mu :{\mathbb {R}}\rightarrow {\mathbb {R}}\) is continuously differential. Then, it holds
with a constant C independent of h.
Proof
We first estimate
and show in the following
Using the inverse estimate (2.25), we conclude the assertion.
We now show (D.1) by an Aubin–Nitsche trick. We define \(e = (\textrm{Id}- R_h)w\), for some \(w\in H^1_0(\varOmega _h)\), and consider the solution \(z \in H^2(\varOmega ) \cap H^1_0(\varOmega )\) of
This gives
The first term is bounded using (2.22) and elliptic regularity by
and, using the geometric estimates in [16, Lem. 8.24], for the second term it holds
By the definition of e and \(R_h\), we have due to \(I_hz \in V_h\)
and the claim follows. \(\square \)
With this, we obtain the boundedness in the discrete chain rule.
Proof
(of Lemma 5.3) We use the definition of \(\mathrm {\Delta }_h\) in (2.9) to obtain
The idea now is to express the integral in terms of \(\mathrm {\Delta }_hu_h\) and \(\mathrm {\Delta }_hw_h\) and lower-order terms, where the is no gradient on \(\varphi _h\). Employing the identities
we derive
This yields with the stability of \(R_h\) shown in Lemma D.1 the estimate
We then use Lemma 3.3 in the form \( \left\Vert \psi _h \right\Vert _{W^{1,N+\delta }} \lesssim \left\Vert \mathrm {\Delta }_h\psi _h \right\Vert _{L^2},\) and thus, the first two terms are bounded. The other two are similar to each other, and it thus suffices to bound
where we again used the maximum norm bounds \(u_h\) and \(w_h\) and \(\mu \in C^2({\mathbb {R}})\), and the claim is shown. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dörich, B. Strong Norm Error Bounds for Quasilinear Wave Equations Under Weak CFL-Type Conditions. Found Comput Math (2024). https://doi.org/10.1007/s10208-024-09639-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10208-024-09639-w
Keywords
- Error analysis
- Full discretization
- Quasilinear wave equation
- Nonconforming space discretization
- Isoparametric finite elements
- A-priori error bounds