Introduction

A central topic in quantum information theory is entanglement theory1. Since quantum entanglement is a valuable resource for quantum metrology2, quantum computation3,4, quantum key distribution5 and anonymous quantum conference key agreement6, bundles of experimental effort have been devoted to create more entangled state7,8,9,10, and series of theoretical works have contributed to characterize different types of entanglement11,12,13.

A quantum state is said to be entangled if it is not a convex combination of product states. To detect the quantum entanglement of two particles, witnesses14,15 (often related to the fidelity of a target state11,16,17) and the PPT criterion18 are standard methods. In the multiparticle case a state can be entangled, but it is still a convex combination of states which are separable for the different bipartitions, then it is called biseparable13. If the state cannot be written as a convex combination of any biseparable states, it is said to be genuine multiparticle entangled (GME)11,12,13. As for the detection of GME states, the fidelity with a highly entangled state, such as the Greenberger-Horne-Zeilinger (GHZ) state is one of the most used in experiments7,19. For example, an n-partite state with a GHZ fidelity exceeding 1/2 is GME. Including GHZ state as a special example, graph states20,21,22 play an eminent role in entanglement theory and its applications.

Recently, the concept of genuine multiparticle entanglement has been debated23,24, and novel notions appropriate for the network scenario have been introduced and studied25,26,27. In a network, states can be prepared by distributing particles from multiple smaller sources to different parties and applying local channels, see Fig. 1 for an example. In this fundamental scenario the local operations rely on a globally shared classical variable (Local operations and shared randomness, LOSR), e.g., a predefined protocol with shared randomness. The scenario of local operations assisted by classical communication (LOCC) gives more power to create distributed quantum states. But, communication based on outcome of local operations requires considerable time, either in the scenario of distributed quantum computation where local operations takes a while, or in the case that nodes in the network are far away from each other. Consequently, it would also require the usage of quantum memories or feed-forward techniques, which are expensive resources for current quantum technologies. Moreover, device-independent quantum information protocols are frequently related to Bell scenarios, where communication is impossible due to the space-like separation. Overall, an n-partite state is called genuine network multipartite entangled (GNME) if it cannot be created via LOSR in the network approach using (n − 1)-partite sources only. Besides this, other quantum correlations like quantum nonlocality and quantum steering have also been generalized to quantum networks recently28,29,30,31,32,33,34,35.

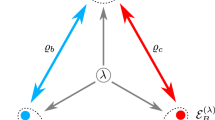
Fig. 1: Sketch of a triangle quantum network.
figure 1

Here three bipartite sources ςa, ςb and ςc are distributed to three parties A, B, C, e.g., the source states ςa are sent to B and C. Each party can apply local operations \({{{{\mathcal{E}}}}}_{X}^{(\lambda )}\) (X = A, B, C) on the received particles, which are affected by global shared randomness λ.

Full size image

For three-qubit states in the triangle network, a witness derived from the fidelity25,34 and semidefinite programming methods based on the inflation technique25,36 can be useful. The disadvantage of these approaches is that both of them are hard to generalize to more complicated quantum networks. An analytical method based on symmetry analysis and inflation techniques37 was proposed recently27 and can overcome some of the difficulties. Explicitly, it was shown there that all n-qubit graph states with n≤12 are not available in networks with bipartite sources, and it was conjectured that this no-go theorem hold for multi-qubit graph states with an arbitrary number of particles.

In this paper we prove that all multi-qudit graph states with a connected graph, where the multiplicities of the edges are either constant or zero, cannot be prepared in any network with only bipartite sources. In fact, this result holds also for all the states whose fidelity with some of those qudit graph states exceeds a certain value. More specifically, our results exclude the generation of any multi-qubit graph state with a fidelity larger than 9/10 in networks. This proves the conjecture formulated in ref. 27, it also may provide interesting connections to other no-go theorems on the preparability of graph states in different physical scenarios, such as spin-models with two-body interactions38,39.

Results

Preliminaries

Network entanglement

The definition of network entanglement is best explained using the example of the triangle scenario, see Fig. 1. Here, one has three bipartite quantum source states ςx for x = a, b, c, and three local channels \({{{{\mathcal{E}}}}}_{{{{\rm{X}}}}}^{(\lambda )}\) for X = A, B, C, where λ is the shared random variable with probability pλ. The global state can be prepared in this scenario has the form

$$\varrho =\mathop{\sum}\limits_{\lambda }{p}_{\lambda }{{{{\mathcal{E}}}}}_{{{{\rm{A}}}}}^{(\lambda )}\otimes {{{{\mathcal{E}}}}}_{{{{\rm{B}}}}}^{(\lambda )}\otimes {{{{\mathcal{E}}}}}_{{{{\rm{C}}}}}^{(\lambda )}\left[{\varsigma }_{{{{\rm{a}}}}}\otimes {\varsigma }_{{{{\rm{b}}}}}\otimes {\varsigma }_{{{{\rm{c}}}}}\right].$$
(1)

For a given state ϱ, the question arises whether it can be generated in this manner, and this question was in detail discussed in refs. 25,26,27.

More generally, one can introduce quantum network states as follows: A given hypergraph G(V, E), where V is the set of vertices and E is the set of hyperedges (i.e., sets of vertices) describes a network where each vertex stands for a party and each hyperedge stands for a source which dispatches particles to the parties represented by the vertices in it. This quantum network is a correlated quantum network (CQN), if each party can apply a local channel depending on a shared random variable. Then, in complete analogy to the definition in Eq. (1) one can ask whether a state can be prepared in this network or not. More properties of these sets of states (e.g., concerning the convex structure and extremal points) can be found in refs. 25,27.

Three-qudit GHZ states and the inflation technique

The inflation technique37 turns out to be an useful tool to study network entanglement25,27. Unless otherwise stated, we consider networks with bipartite sources only. For a given network as the triangle network depicted in Fig. 1 and also in Fig. 2a, the copies of sources are sent to different copies of the parties as in Fig. 2b, c. In principle, the source states may also be wired differently in different kinds of inflation. For convenience, here we use also edges with only one vertex as in Fig. 2d, e, which means that the particles, which have not appeared in the state, are traced out in the source states.

Fig. 2: Relevant inflations of the triangle network for GHZ state.
figure 2

The triangle network in a and two kinds of its inflation in b and c. For convenience, we use d and e as short notations of b and c, respectively. Here the broken edge e with only one vertex v means that we ignore or trace out the particles not for the party represented by v from the source state represented by e.

Full size image

The key idea of the inflation method is the following: If the three-particle state ρ can be prepared in the network, the six-particle states γ and η can be prepared in the inflated networks as well. The states γ and η share some marginals with ρ and with each other. So, if one can prove that six-particle states with these desired properties do not exist, the state ρ is not reachable in the original network.

To see how the idea of inflation works in practice, we take the three-qudit GHZ state40 as an example. The three-qudit GHZ state \(\left\vert {{{\rm{GHZ}}}}\right\rangle =1/\sqrt{d}\mathop{\sum }\nolimits_{i = 0}^{d-1}\left\vert iii\right\rangle\) is a stabilizer state, whose stabilizers include

$$\begin{array}{r}{Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{A}}}}}^{{\dagger} },{Z}_{{{{\rm{A}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} },{Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} },{X}_{{{{\rm{A}}}}}{X}_{{{{\rm{B}}}}}{X}_{{{{\rm{C}}}}},\end{array}$$
(2)

where the unitary operators are \(Z=\mathop{\sum }\nolimits_{q = 0}^{d-1}{\omega }^{q}\left\vert q\right\rangle \left\langle q\right\vert ,X=\mathop{\sum }\nolimits_{q = 0}^{d-1}\left\vert q\oplus 1\right\rangle \left\langle q\right\vert ,\) with ⊕ to be the addition modulo d, and \(\omega =\exp \frac{2\pi i}{d}\). Note XmZn = ω−mnZnXm.

For a given network state ρ, we can consider the value ⌈M⌉ρ of any stabilizer M in Eq. (2), i.e., the expectation value \({\langle {\Pi }_{M}^{(1)}\rangle }_{\rho }\) with \({\Pi }_{M}^{(1)}\) to be the projector into the eigenspace of M with eigenvalue + 1. If one of ⌈M⌉ρ does not equal to 1, we can conclude that this network state ρ cannot be the state \(\left\vert {{{\rm{GHZ}}}}\right\rangle \left\langle {{{\rm{GHZ}}}}\right\vert\).

Let us consider two kinds of inflation of the triangle-network as in Fig. 2, where the corresponding network states are denoted as γ, η. Roughly speaking, the source between B, C is broken in the γ inflation. Note that inflation η is actually a trivial inflation in triangular network. By comparing Fig. 2a–c, we have the marginal relations

$${\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{A}}}}}^{{\dagger} }\rceil }_{\gamma }={\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{A}}}}}^{{\dagger} }\rceil }_{\rho },{\lceil {Z}_{{{{\rm{A}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\gamma }={\lceil {Z}_{{{{\rm{A}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\rho },$$
(3)
$${\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\eta }={\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\gamma },$$
(4)
$${\lceil {({X}_{{{{\rm{A}}}}}{X}_{{{{\rm{B}}}}}{X}_{{{{{\rm{C}}}}}^{{\prime} }})}^{\left\lfloor \frac{d}{2}\right\rfloor }\rceil }_{\eta }={\lceil {({X}_{{{{\rm{A}}}}}{X}_{{{{\rm{B}}}}}{X}_{{{{\rm{C}}}}})}^{\left\lfloor \frac{d}{2}\right\rfloor }\rceil }_{\rho }.$$
(5)

For convenience, here \({\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\eta }\) stands for \({\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{{\eta }_{{{{\rm{BC}}}}}}\), where ηBC is the reduced state of η on parties B and C. We use such shorthand notations throughout the whole manuscript without confusion. By applying Lemma 4 (see Supplementary Note 1 for the lemma and its proof), we have

$$\begin{array}{r}{\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\gamma }\ge {\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{A}}}}}^{{\dagger} }\rceil }_{\gamma }+{\lceil {Z}_{{{{\rm{A}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\gamma }-1.\end{array}$$
(6)

Under the assumption that \({\lceil {({X}_{{{{\rm{A}}}}}{X}_{{{{\rm{B}}}}}{X}_{{{{{\rm{C}}}}}^{{\prime} }})}^{\left\lfloor \frac{d}{2}\right\rfloor }\rceil }_{\eta }\ge 1/2\) and \({\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\eta }\ge 1/2\), Lemma 5–7 (see Supplementary Note 1 for statements and their proofs), lead to

$$\begin{array}{r}| 2{\lceil {({X}_{{{{\rm{A}}}}}{X}_{{{{\rm{B}}}}}{X}_{{{{{\rm{C}}}}}^{{\prime} }})}^{\left\lfloor \frac{d}{2}\right\rfloor }\rceil }_{\eta }-1{| }^{2}+| 2{\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\eta }-1{| }^{2}\le 1+\sin {\theta }_{d},\end{array}$$
(7)

where θd = 0 when d is even and \({\theta }_{d}=\frac{\pi }{2d}\) when d is odd. This assumption can be ensured whenever \({{{\mathcal{F}}}}(\left\vert {{{\rm{GHZ}}}}\right\rangle \left\langle {{{\rm{GHZ}}}}\right\vert ,\rho )\ge 3/4\) according to Lemma 5 (see Supplementary Note 1 for Lemma 5).

If ρ is indeed the GHZ state, then Eq. (3)–(7) cannot hold simultaneously, which is a contradiction. Combined with Lemma 5 (see Supplementary Note 1), which implies \({\lceil {({X}_{{{{\rm{A}}}}}{X}_{{{{\rm{B}}}}}{X}_{{{{{\rm{C}}}}}^{{\prime} }})}^{\left\lfloor \frac{d}{2}\right\rfloor }\rceil }_{\eta }\ge {{{\mathcal{F}}}}\) and \({\lceil {Z}_{{{{\rm{B}}}}}{Z}_{{{{\rm{C}}}}}^{{\dagger} }\rceil }_{\eta }\ge 2{{{\mathcal{F}}}}-1\), Eq. (7) can be solved as

$$\frac{3}{4}\le {{{\mathcal{F}}}}(\left\vert {{{\rm{GHZ}}}}\right\rangle \left\langle {{{\rm{GHZ}}}}\right\vert ,\rho )\le \frac{7+\sqrt{4+5\sin {\theta }_{d}}}{10}.$$
(8)

Hence, either the assumption does not hold, then \({{{\mathcal{F}}}}(\left\vert {{{\rm{GHZ}}}}\right\rangle \left\langle {{{\rm{GHZ}}}}\right\vert ,\rho ) < 3/4\); or the assumption holds and so do the inequalities in Eq. (8). Since the upper bound in Eq. (8) is always larger than 3/4 for any dimension d, the upper bound in Eq. (8) holds whatever the assumption holds or not. We remark that we only used GHZ states as an example to introduce our general method, a tighter bound on the fidelity exists (see Supplementary Note 4.B for discussions; see also25).

Multi-qudit graph states

The three-qudit GHZ state is a special case of a multi-qudit graph state22. In the same spirit, we can also derive no-go theorems for network states with multi-qudit graph states as targets. Each graph state is associated with a multigraph G = (V, E), defined by its vertex set V, and the edge set E, where the edge between vertices i, j with multiplicity mij is denoted as ((i, j), mij). Without loss of generality, we will only consider multi-partite graph states, i.e. number of parties (vertices) is at least 3. Due to the periodicity as follows, the multiplicity can be limited to mij = 0, 1, ⋯ , d − 1, where d is dimension of Hilbert space for a single qudit. Besides, we denote Ni the neighborhood of vertex i, and define unitary stabilizers \({g}_{i}={X}_{i}{\otimes }_{j\in {N}_{i}}{Z}^{{m}_{ij}}\). Note that \({g}_{i}^{d}=I\). For a given multigraph G = (V, E), the corresponding graph state is the unique common eigenvector of the operators \({\{{g}_{i}\}}_{i\in V}\) with eigenvalue + 122,41,42,43. This eigenvector \(\left\vert G\right\rangle\) is called the graph state associated to the graph G.

Main results

Let us now introduce our main result, stating that graph states and certain multi-qudit graph states cannot be generated in any network with bipartite sources.

Theorem 1

Multi-qudit graph states with connected graph and multiplicities either being constant m or 0 cannot be prepared in any network with bipartite sources.

Proof

Here we explain the main idea (see Supplementary Note 2 for the detailed proof). The structure of the proof is in the same spirit as the one for \(\left\vert {{{\rm{GHZ}}}}\right\rangle\) state. The key point is to keep necessary marginal relations in different kinds of inflations and finally derive a contradiction.

For a connected graph G with no less than three vertices, there are always three vertices A, B, C such that (A, B), (A, C) are two edges. If (B, C) is not an edge, we call (A, B, C) an angle. Otherwise, we call (A, B, C) a triangle.

To carry out the proof, we have to carefully group the neighborhoods of vertices A, B, C and choose proper stabilizers of the graph state correspondingly. Here we consider the case where (A, B, C) is a triangle as an example. Then we can partition all the vertices into 4 groups as in Fig. 3, where TABC is the common neighborhood of A, B, C, JAB is the common neighborhood of A, B but not C, EA is the neighborhood which is not shared by B, C and so on.

Fig. 3: Fully connected network with bipartite sources and two kinds of its inflation.
figure 3

Here the corresponding states are denoted as ρ, γ and η. The sources which have not been changed in the whole proof are omitted in the figure. The original network in a and two kinds of its inflation in b and c.

Full size image

By choosing \({S}_{1}={g}_{{{{\rm{A}}}}}{g}_{{{{\rm{B}}}}}^{{\dagger} }\), \({S}_{2}={g}_{{{{\rm{A}}}}}^{{\dagger} }{g}_{{{{\rm{C}}}}}\), \({S}_{3}={S}_{1}{S}_{2}={g}_{{{{\rm{B}}}}}^{{\dagger} }{g}_{{{{\rm{C}}}}}\) and \({S}_{4}={g}_{{{{\rm{C}}}}}^{t}\) (the t-th power of gC), we have the marginal relations

$${\lceil {S}_{1}\rceil }_{\gamma }={\lceil {S}_{1}\rceil }_{\rho },{\lceil {S}_{2}\rceil }_{\gamma }={\lceil {S}_{2}\rceil }_{\rho },$$
(9)
$${\langle {S}_{3}\rangle }_{\eta }={\langle {S}_{3}\rangle }_{\gamma },{\langle {S}_{{4}^{{\prime} }}\rangle }_{\eta }={\langle {S}_{4}\rangle }_{\rho },$$
(10)

where \({S}_{{4}^{{\prime} }}\) is related to S4 by changing party \({{{{\rm{C}}}}}^{{\prime} }, E_{\rm{C}}^{\prime}\) in the support to C, EC. These marginal relations can be verified by comparing the supports of each operator in different kinds of inflation. For instance, the support of S1 is A, B, JAB, JBC, JCA, TABC.

However, \({S}_{3},{S}_{{4}^{{\prime} }}\) do not commute in the inflation η. More precisely, we have that

$$| {\langle {S}_{3}\rangle }_{\eta }{| }^{2}+| {\langle {S}_{{4}^{{\prime} }}\rangle }_{\eta }{| }^{2}\le 1+\sin {\theta }_{t,d},$$
(11)

where 0 ≤ θt,d ≤ π/6 by choosing t properly.

Similarly as the analysis for the GHZ state, the relation that S3 = S1S2 and conditions in Eqs. (9)–(11)) lead to

$${{{\mathcal{F}}}}(\left\vert G\right\rangle \left\langle G\right\vert ,\rho )\le \frac{7+\sqrt{4+5\sin ({\theta }_{t,d})}}{10} < 0.95495.$$
(12)

This is in fact a universal bound for arbitrary configuration of equal-multiplicity multi-qudit graph states.

Note that for qubit graph states, the multiplicity is either 1 or 0, this leads to the following theorem.

Theorem 2

Any multi-qubit graph state with connected graph cannot be prepared in a network with only bipartite sources, with 9/10 as an upper bound of fidelity between graph state and network state. This follows from the fact that θt,2 = 0.

In order to formulate a more general statement, note that the key ingredients in the proof of Theorem 1, were that all parties can be grouped in a special way which fits to the algebraic relations S3 = S1S2 for commuting S1, S2, moreover, it was needed that \({S}_{3},{S}_{{4}^{{\prime} }}\) have no common eigenvectors with eigenvalue + 1. This leads to a a more general theorem for the states with a set of stabilizers.

Theorem 3

For a given pure state σ with commuting (unitary or projection) stabilizers {S1, S2, S3 = S1S2, S4}, it cannot be prepared in bipartite network if

  1. 1.

    all the parties can be grouped into \({\{{G}_{i}\}}_{i = 1}^{4}\) such that Si has no support in Gi, see also Fig. 4a;

    Fig. 4: General inflation scheme in bipartite network similar to Fig. 3.
    figure 4

    In a, Gi’s are group of parties in a partition, the green, red, blue and dashed circles stand for the supports for operators S1, S2, S3, S4, respectively. In b, c, and d, we replace the label of each group by the indices of the Si’s which has this group as support. The green shadow represents a multipartite source relating to all the groups in it. The sources which have not been changed in the whole proof are omitted in the figures.

    Full size image
  2. 2.

    S1, S2 commutes, and \({S}_{3},{S}_{{4}^{{\prime} }}\) have no common eigenvectors with eigenvalue 1, where \({S}_{{4}^{{\prime} }}\) has the support G2, G3 and a copy of G1, and \({S}_{{4}^{{\prime} }}\) acts there same as S4 on supp(S4).

Proof

Here we provide the main steps of the proof without diving into details. The first condition implies that, those four operators do not have common support for all of them. Hence, the set of parties can be divided into the four parts as illustrated in Fig. 4a. By comparing the supports of the operators in different kinds of inflation as in Fig. 4, we have the marginal relations

$${\lceil {S}_{1}\rceil }_{\gamma }={\lceil {S}_{1}\rceil }_{\rho },{\lceil {S}_{2}\rceil }_{\gamma }={\lceil {S}_{2}\rceil }_{\rho },$$
(13)
$${\lceil {S}_{3}\rceil }_{\eta }={\lceil {S}_{3}\rceil }_{\gamma },{\lceil {S}_{{4}^{{\prime} }}\rceil }_{\eta }={\lceil {S}_{4}\rceil }_{\rho }.$$
(14)

Through those marginal relations, we can relate \({\lceil {S}_{3}\rceil }_{\eta }\) and \({\lceil {S}_{{4}^{{\prime} }}\rceil }_{\eta }\) to \(f={{{\mathcal{F}}}}(\sigma ,\rho )\). Finally, the second condition leads to the result that f < 1. In fact,

$$f\le \frac{7+\sqrt{4+5{\lambda }^{{\prime} }/2}}{10} < 1,$$
(15)

where \({\lambda }^{{\prime} } < 2\) is the maximal singular value of \(\{{S}_{3},{S}_{{4}^{{\prime} }}^{{\dagger} }\}\).

Note that all the bipartite sources in the network among parties in supp(S1) have not been touched during the inflation procedure, so the proof still holds even if there is a multipartite source just affecting this set of parties. By exhaustive search and applying Theorem 3 to multi-qudit graph states, we can figure out the situations where all n-partite qudit graph states in dimension d cannot arise from a network with bipartite sources, see Theorem 10, which is a consequence of Theorem 3 (see Supplementary Note 3 for Theorem 10 and its proof). The result is summarized in Table 1. Moreover, any prime-dimensional graph state satisfying special structures as in Theorem 10 cannot be prepared in a network with bipartite sources (see Supplementary Note 3 for discussions).

Table 1 A table of prohibited qudit graph states.
Full size table

Discussion

Here, we have developed a toolbox to compare multi-qudit graph states and states that are generated in a quantum network without memory and feed forward. By combining those tools related to symmetry and the inflation technique, we proved that all multi-qudit graph states, where the non-zero multiplicities are a constant, cannot be prepared in the quantum network with just bipartite sources. The result can also be generalized to a larger class of multi-qudit graph states and quantum networks with multipartite sources, in the case that the generalization does not affect the necessary marginal relations during the inflation procedure. The more general case with multi-partite sources is an interesting topic for future research. Furthermore, we provided a fidelity estimation of the multi-qudit graph states and network states based on a simple analysis.

More effort should be contributed to the fidelity analysis in the future, such as introducing more types of inflation in ref. 27, and generalizing the techniques in ref. 25 for the states other than GHZ states. Another interesting project for further study is to consider other families of states, like Dicke states or multi-particle singlet states, which are not described by a stabilizer formalism. Finally, from the fact that graph states cannot be prepared in the simple model of a network considered here, the question arises, which additional resources (such as classical communication) facilitate the generation of such states. Characterizing these resources will help to implement quantum communication in networks in the real world.

Note added: While finishing this manuscript, we became aware of a related work by O. Makuta et al.44. Albeit those two works originate from the same conjecture in ref. 27, the techniques and results are different from few perspectives. Especially, we have only made use of two kinds of inflation and Theorem 2 here holds for all dimensions but with limited multiplicities. The resulting fidelity between the graphs states and network states has also different estimations. The application of Theorem 3, like in combination with Theorem 10, can cover more situations.