Introduction

Out of all proposed real-life implementations of quantum information, quantum networks stand as one of the most promising ones. We already have many ideas for possible applications of quantum networks such as quantum key distribution1,2,3, clock synchronisation4, parallel computing5 or even quantum internet6,7,8,9. What is more, their relative simplicity as compared with other quantum technologies, makes them perhaps the closest ones to commercial implementation. This sentiment is also supported by the significant progress in the experimental implementation of quantum networks that has recently been made10,11,12,13,14.

At their core, quantum networks are simply collections of parties and of sources of multipartite quantum states. Their most natural model (referred to as LOCC networks) is one that allows the parties to act with the most general local operations on their shares of the distributed states and to coordinate their actions by using classical communication. However, while connected LOCC networks enable preparing any multipartite state, the use of classical communication might be problematic for their commercial implementations.

When considering the possible future applications of quantum networks one has to take into account that the distances between parties will substantially increase as compared to the current state-of-the-art experiments. Therefore, while classical communication between parties can be considered almost instantaneous in a lab setup, this will not be the case for quantum networks spanning many different countries or even continents. Depending on the number of rounds of measurement and communication that have to be performed for a generation of a given state, the delay caused by the travel time of the information could become a substantial factor to the run time of any procedure done via a quantum network. From that point of view, it would be beneficial, e.g. for quantum key distribution protocols, to use quantum states that require as little classical communication as possible to be generated. This has not only the potential to decrease the latency of quantum networks but also to reduce the noise therein, as the longer a quantum state has to be stored, the noisier the state gets.

One is thus forced to consider quantum networks in which the amount of classical communication between the parties is limited or even no communication is allowed (see ref. 15). A possible model of quantum networks that fulfils this requirement is one in which the parties can apply arbitrary quantum channels to their particles, however, they cannot use classical communication. Instead, they are allowed to orchestrate their actions by using some preshared classical information. We call such networks LOSR (local operations and shared randomness) quantum networks. While the above no-communication assumption severely reduces the capability of generating multipartite states in LOSR quantum networks as compared to the LOCC ones, they are still more general than those in which the parties can only implement unitary operations and no randomness is shared. While the LOSR networks have become an object of intensive studies16,17,18,19,20, it remains unclear what multipartite entangled states can actually be prepared in them.

In the quantum information graph states stand as one of the most representative classes of multipartite states, including the Greenberger-Horne-Zeilinger21, cluster22 or the absolutely maximally entangled23 states. Moreover, they are key resources for many applications, just to mention quantum computing24,25,26, multipartite secret sharing27, or quantum metrology28. It has thus been a question of utmost importance whether they can be prepared in quantum networks. While in a LOCC quantum network one can simply generate the graph state locally and then distribute it using quantum teleportation29,30, this strategy cannot be applied in the LOSR case. Therefore, the question remains of whether one can generate graph states in LOSR quantum networks.

Here we answer the above question to the negative and show that no graph states of arbitrary prime local dimension (or any state sufficiently close to them) can be prepared in LOSR networks with bipartite sources. We thus generalise the recent results that the three-partite GHZ states17,31 or any N-qubit graph states with N up to 12 cannot be prepared in such networks19. Simultaneously, our work is complementary to Ref. 20 showing that no qubit or qutrit graph states of an arbitrary number of parties can be prepared in LOSR networks even with (N − 1)-partite sources. Our proof employs the quantum inflation method32,33 which is perfectly suited to tackle these types of questions17,33.

Results

Preliminaries

Graph states

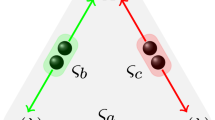
Consider a multigraph G which is a graph in which any two vertices can be connected by more than one edge, but no edge can connect a vertex to itself. Let Γi,j denote the number of edges connecting vertices i and j, and let \({{{{\mathcal{N}}}}}_{i}\) be the neighbourhood of vertex i—the set of vertices that are connected to i by at least one edge (see Fig. 1 for an example). To associate a quantum state to an N-vertex multigraph G, we consider a Hilbert space \({{{\mathcal{H}}}}={{\mathbb{C}}}_{d}^{\otimes N}\), where each qudit space \({{\mathbb{C}}}_{d}\) corresponds to one of the vertices of G; we assume that d is prime and fulfils \(d-1\geqslant \mathop{\max }\nolimits_{i,j}{{{\Gamma }}}_{i,j}\). To each vertex i we associate the following operator

$${g}_{i}={X}_{i}\mathop{\prod}\limits_{j\in {{{{\mathcal{N}}}}}_{i}}{\left({Z}_{j}\right)}^{{{{\Gamma }}}_{i,j}},$$
(1)

where X and Z are generalised Pauli matrices,

$$X=\mathop{\sum }\limits_{i=0}^{d-1}\left\vert i+1\right\rangle \left\langle i\right\vert ,\qquad Z=\mathop{\sum }\limits_{i=0}^{d-1}{\omega }^{i}\left\vert i\right\rangle \left\langle i\right\vert ,$$
(2)

with \(\omega =\exp (2\pi {{{\rm{i}}}}/d)\) and \(\left\vert d\right\rangle \equiv \left\vert 0\right\rangle\). The subscripts in (1) label the subsystems on which these operators act. One defines a graph state \(\left\vert G\right\rangle\) associated to G to be the unique state in \({{{\mathcal{H}}}}\) obeying \({g}_{i}\left\vert G\right\rangle =\left\vert G\right\rangle (i=1,\ldots ,N)\) (for a review see34).

Fig. 1: Exemplary multigraph.
figure 1

A an example of multigraph with three vertices.

Full size image

Quantum networks

Let us consider a scenario in which N parties, labelled 1, …, N, receive quantum states distributed by independent sources. Each party i can perform an arbitrary local operation represented by a quantum channel \({{{{\mathcal{E}}}}}_{i}\), on their shares of these states. We also assume that parties cannot communicate with each other, yet they all have access to some shared randomness, which is a random variable λ with a distribution pλ. These assumptions describe a scenario called LOSR.

There is one more assumption, independent of LOSR, that we make: the sources distributing quantum states are bipartite, i.e., a single source distributes a quantum state to two parties. We say that two parties are connected if they share a state.

The most general state that can be produced in an LOSR network is given by19

$$\rho =\mathop{\sum}\limits_{\lambda }{p}_{\lambda }{{{{\mathcal{E}}}}}_{1}^{\lambda }\otimes \cdots \otimes {{{{\mathcal{E}}}}}_{N}^{\lambda }\left[{\sigma }_{1,2}\otimes {\sigma }_{1,3}\otimes \cdots \otimes {\sigma }_{N-1,N}\right],$$
(3)

where σi,j denotes a state distributed between parties i and j, ∑λpλ = 1, and the subscript λ denotes the dependence of local operations on the shared random variable.

Here, three remarks are in order. First, tensor products of \({{{{\mathcal{E}}}}}_{i}^{\lambda }\) and of σi,j are taken with respect to different sets of subsystems; while the former is taken with respect to different parties, the latter separates states from different sources.

Second, we should expect the distributed states σi,j to depend on λ because the sources can be classically correlated as well. However, since we do not impose any restriction on the dimension of σi,j, one can get rid of this dependency by considering a Hilbert space of sufficiently high dimension17.

Third, in this work, we will assume that every network we consider (not including inflations) is fully connected, i.e., each party shares a bipartite state with every other party. We can make this assumption without loss of generality because the behaviour of each quantum network can always be simulated by the fully connected one: taking σi,j to be the maximally mixed state produces the same outcomes as removing the connection between the nodes i and j. In other words, if ρ cannot be generated in an N-partite LOSR network with bipartite sources that is fully connected, then it cannot be generated in any such network which is not fully connected.

Network inflation

Let us briefly describe here the network inflation method32,33 which we use to derive our main result. Given some network \({{{\mathcal{O}}}}\), the inflation \({{{\mathcal{I}}}}\) of \({{{\mathcal{O}}}}\) is a network that consists of multiple copies of parties and sources from the original network. Whether two parties are connected in \({{{\mathcal{I}}}}\) is up to us, the only restriction is that they are connected via a copy of a source from \({{{\mathcal{O}}}}\).

This construction is very general as many different inflations can be considered for a given network \({{{\mathcal{O}}}}\). However, here we focus on a certain class of inflations that are tailored to our proof. Consider an N-partite network \({{{\mathcal{O}}}}\) that we want to analyse; as already explained, we assume it to be fully connected. In our approach, every inflation \({{{\mathcal{I}}}}\) of \({{{\mathcal{O}}}}\) consists of two copies of the parties from \({{{\mathcal{O}}}}\) labelled 1, …, N and \({1}^{{\prime} },\ldots ,{N}^{{\prime} }\). We assume that parties i and \({i}^{{\prime} }\) apply the same local operation as the original one: \({{{{\mathcal{E}}}}}_{i}^{{{{\mathcal{I}}}}}={{{{\mathcal{E}}}}}_{{i}^{{\prime} }}^{{{{\mathcal{I}}}}}={{{{\mathcal{E}}}}}_{i}^{{{{\mathcal{O}}}}}\), where the superscripts indicate the network. We also assume that each party i in \({{{\mathcal{I}}}}\) is connected to either j or \({j}^{{\prime} }\) but never to both, and that two copies of the same party i and \({i}^{{\prime} }\) are never connected to each other. Furthermore, if two copies of parties share a state, this state is a copy of a state shared between original parties in \({{{\mathcal{O}}}}\). These last two assumptions imply that for every pair of parties \(i,j\in {{{\mathcal{O}}}}\) and any inflation \({{{\mathcal{I}}}}\), exactly one of the following statements is true:

$${\sigma }_{i,j}^{{{{\mathcal{I}}}}}={\sigma }_{{i}^{{\prime} },{j}^{{\prime} }}^{{{{\mathcal{I}}}}}={\sigma }_{i,j}^{{{{\mathcal{O}}}}},\quad {{{\rm{or}}}}\quad {\sigma }_{i,{j}^{{\prime} }}^{{{{\mathcal{I}}}}}={\sigma }_{{i}^{{\prime} },j}^{{{{\mathcal{I}}}}}={\sigma }_{i,j}^{{{{\mathcal{O}}}}}.$$
(4)

We finally assume that in \({{{\mathcal{I}}}}\) the shared randomness is distributed between all copies of parties, meaning that the state generated in \({{{\mathcal{I}}}}\) is described by Eq. (3).

The above assumptions allow us to establish very useful relations between expected values \({\langle \cdot \rangle }_{{{{{\mathcal{I}}}}}_{1}}\) and \({\langle \cdot \rangle }_{{{{{\mathcal{I}}}}}_{2}}\) calculated over states from two different inflations \({{{{\mathcal{I}}}}}_{1},{{{{\mathcal{I}}}}}_{2}\). To this end, let us introduce an isomorphism \(\chi :{{{{\mathcal{I}}}}}_{1}\to {{{{\mathcal{I}}}}}_{2}\) with an associated set Sχ ⊂ {1, …, N}, that acts by swapping labels of parties i and \({i}^{{\prime} }\) for all i ∈ Sχ. If an operator M is a 2N-fold tensor product, then we use the notation χ(M) for a swap operation between parties i and \({i}^{{\prime} }\) for all i ∈ Sχ. With this we formulate the following fact.

Fact 1

Consider a network \({{{\mathcal{O}}}}\) and two different inflations of it, \({{{{\mathcal{I}}}}}_{1}\) and \({{{{\mathcal{I}}}}}_{2}\). Consider also two matrices \(B\,{= \bigotimes}_{i\in {{{{\mathcal{I}}}}}_{1}}{B}_{i}\) and \(C\,{ = \bigotimes }_{i\in {{{{\mathcal{I}}}}}_{2}}{C}_{i}\) that act nontrivially on some subnetworks \({{{{\mathcal{I}}}}}_{i}^{{\prime} }\subseteq {{{{\mathcal{I}}}}}_{i}\). Then, \({\langle B\rangle }_{{{{{\mathcal{I}}}}}_{1}}={\langle C\rangle }_{{{{{\mathcal{I}}}}}_{2}}\) if there exists an isomorphism χ such that

$$\chi ({{{{\mathcal{I}}}}}_{1}^{{\prime} })={{{{\mathcal{I}}}}}_{2}^{{\prime} }\quad {{{\rm{and}}}}\quad \chi (B)=C.$$
(5)

The above fact can be proven by using the decomposition of the state in LOSR network (3), taking out the sum over λ out of the trace, and then tracing out the parties where B and C act trivially.

Main results

Let us now move on to the main results of our work, namely that no graph state can be generated in quantum networks with bipartite sources. We begin by presenting the key ingredients of our approach, which is inspired by the recent work19. The main idea of the proof is to show that the assumption that a graph state can be generated in a network leads to the violation of a certain inequality that follows from the lemma below (see Supplementary Note 1 for a proof and Supplementary Note 2 for an alternative approach).

Lemma 1

Consider two unitary matrices A1, A2 acting on some Hilbert space \({{\mathbb{C}}}_{D}\) with D being a multiple of some prime number d ≥ 2. Assume moreover that Ai satisfy \({A}_{1}^{d}={A}_{2}^{d}={\mathbb{1}}\) and A1A2 = ωqA2A1 for some q ∈ {1, …, d − 1}. Then

$$\mathop{\sum }\limits_{k=0}^{d-1}\left\langle {A}_{1}^{k}+{A}_{2}^{k}\right\rangle \,\leqslant\, d+\sqrt{d},$$
(6)

where \(\langle \cdot \rangle \equiv {{{\rm{Tr}}}}[\rho (\cdot )]\) and the above holds true for any state ρ acting on \({{\mathbb{C}}}_{D}\).

In order to show a violation of (6) we also need the following fact.

Fact 2

Consider three mutually commuting unitary matrices Bi that obey \({B}_{i}^{d}={\mathbb{1}}\). If \(\langle {B}_{1}{B}_{3}\rangle =\langle {B}_{2}{B}_{3}^{{\dagger} }\rangle =1\), then 〈B1B2〉 = 1.

This fact follows from an observation that B1B3 and \({B}_{2}{B}_{3}^{{\dagger} }\) are unitary and therefore the fact that \(\langle {B}_{1}{B}_{3}\rangle =\langle {B}_{2}{B}_{3}^{{\dagger} }\rangle =1\) holds true for some \(\left\vert \psi \right\rangle\) implies that \({B}_{1}{B}_{3}\left\vert \psi \right\rangle =\left\vert \psi \right\rangle\) and \({B}_{2}{B}_{3}^{{\dagger} }\left\vert \psi \right\rangle =\left\vert \psi \right\rangle\). Since Bi mutually commute, one concludes that \({B}_{1}{B}_{2}\left\vert \psi \right\rangle =\left\vert \psi \right\rangle\) which gives the above implication.

Facts 1 and 2 together with Lemma 1 are the key elements of our approach. However, before showing how they are combined into proof, let us present an illustrative example (for an extensive explanation of the inflation technique see Supplementary Note 3). Let us fix d = 3 and consider the triangle network \({{{{\mathcal{O}}}}}^{{{\Delta }}}\) presented in Fig. 2 and the graph state \(\left\vert {G}_{{{\Delta }}}\right\rangle\) corresponding to the triangle graph shown in Fig. 1, i.e., one that satisfies \({g}_{i}\left\vert {G}_{{{\Delta }}}\right\rangle =\left\vert {G}_{{{\Delta }}}\right\rangle\) for

$${g}_{1}={X}_{1}{Z}_{2}^{2}{Z}_{3},\qquad {g}_{2}={Z}_{1}^{2}{X}_{2},\qquad {g}_{3}={Z}_{1}{X}_{3}.$$
(7)

In what follows we prove that this state cannot be generated in \({{{{\mathcal{O}}}}}^{{{\Delta }}}\). Our proof is by contradiction.

Fig. 2: Exemplary network with its inflations.
figure 2

A fully connected tripartite quantum network \({{{{\mathcal{O}}}}}^{{{\Delta }}}\) with its two inflations \({{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}\) and \({{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}\). The edges represent bipartite states shared by the parties.

Full size image

Let us consider an inflation of \({{{{\mathcal{O}}}}}^{{{\Delta }}}\), denoted \({{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}\) [cf. Fig. 2], and two operators defined on it, g1, acting only on non-primed parties, and \({Z}_{1}^{2}{X}_{{2}^{{\prime} }}\). Due to the fact that they overlap only on the non-primed party 1, it follows that \({g}_{1}{Z}_{1}^{2}{X}_{{2}^{{\prime} }}=\omega {Z}_{1}^{2}{X}_{{2}^{{\prime} }}{g}_{1}\), and thus Lemma 1 implies that

$$\mathop{\sum }\limits_{k=0}^{2}\left({\left\langle {g}_{1}^{k}\right\rangle }_{{{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}}+{\left\langle {({Z}_{1}^{2}{X}_{{2}^{{\prime} }})}^{k}\right\rangle }_{{{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}}\right)\,\leqslant\, 3+\sqrt{3},$$
(8)

where \({\langle \cdot \rangle }_{{{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}}\) denotes the expected value calculated on any state that can be generated in \({{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}\). Our goal is to show that the assumption that the graph state \({\left\vert G\right\rangle }_{{{\Delta }}}\) can be generated in \({{{{\mathcal{O}}}}}^{{{\Delta }}}\) leads to violation of inequality (8). We achieve this by proving that, under the above assumption, every expected value in (8) equals one.

Let us focus on the first expected value in (8). Given that \(\left\vert {G}_{{{\Delta }}}\right\rangle\) can be prepared in \({{{{\mathcal{O}}}}}^{{{\Delta }}}\), by tracing out all primed parties we get \({\langle {g}_{1}^{k}\rangle }_{{{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}}={\langle {g}_{1}^{k}\rangle }_{{{{{\mathcal{O}}}}}^{{{\Delta }}}}=1\). As for the second expected value in (8), we can use Fact 1 to show that

$${\left\langle {Z}_{1}^{2}{X}_{{2}^{{\prime} }}\right\rangle }_{{{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}}={\left\langle {g}_{2}\right\rangle }_{{{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}},$$
(9)

where \({{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}\) is another inflation of \({{{{\mathcal{O}}}}}^{{{\Delta }}}\) presented in Fig. 2.

Let us now prove that \({\langle {g}_{2}\rangle }_{{{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}}=1\). Since the nodes 1 and 2 are disconnected in \({{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}\) we cannot directly obtain this expected value from the original network \({{{{\mathcal{O}}}}}^{{{\Delta }}}\) and the state \(\left\vert {G}_{{{\Delta }}}\right\rangle\); still, we can compute it indirectly by employing Fact 2. To this aim, we first notice that by tracing out all primed parties we get implies that \({\langle {g}_{2}{g}_{3}\rangle }_{{{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}}={\langle {g}_{2}{g}_{3}\rangle }_{{{{{\mathcal{O}}}}}^{{{\Delta }}}}=1\) and \({\langle {g}_{3}^{2}\rangle }_{{{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}}={\langle {g}_{3}^{2}\rangle }_{{{{{\mathcal{O}}}}}^{{{\Delta }}}}=1\). Since the three generators gi mutually commute, one concludes from Fact 2 that \({\langle {g}_{2}{g}_{3}\rangle }_{{{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}}=1={\langle {g}_{3}^{2}\rangle }_{{{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}}\) implies \({\left\langle {g}_{2}\right\rangle }_{{{{{\mathcal{I}}}}}_{1}^{{{\Delta }}}}=1\), which is what we wanted to obtain.

Hence, Eq. (9) implies that \({\left\langle {Z}_{1}^{2}{X}_{{2}^{{\prime} }}\right\rangle }_{{{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}}=1.\) By the same argument we have \({\left\langle {Z}_{1}{X}_{{2}^{{\prime} }}^{2}\right\rangle }_{{{{{\mathcal{I}}}}}_{0}^{{{\Delta }}}}=1,\) which implies that the left side of (8) equals six, leading to a contradiction. Thus, the triangle graph state cannot be prepared in the network \({{{{\mathcal{O}}}}}^{{{\Delta }}}\).

We are now ready to present our main result that no graph states of arbitrary local prime dimension can be produced in LOSR quantum networks with bipartite sources, generalizing the results of Refs. 19,20.

Theorem 1

Consider a graph G with N ⩾ 3 vertices and where at least one vertex i has a neighbourhood \(| {{{{\mathcal{N}}}}}_{i}| \,\geqslant\, 2\). The graph state \(\left\vert G\right\rangle \in {{\mathbb{C}}}_{d}^{\otimes N}\), where d is prime, corresponding to a graph G cannot be generated in an LOSR N-partite quantum network with bipartite sources.

Proof

The proof is highly technical, and so we present it in Supplementary Note 4. Here we describe its key ideas.

First, in every graph satisfying the assumptions of Theorem 1 we can relabel vertices so that \(| {{{{\mathcal{N}}}}}_{1}\setminus {{{{\mathcal{N}}}}}_{2}| \,\geqslant\, 2\) and Γ1,2 ≠ 0. Next, we utilise a graph transformation called local complementation (see refs. 35,36) to divide the set of all graph states into four, distinct subsets. Since the proof for three of those classes is relatively simple, here we discuss only the most complicated case of graphs for which \({{{{\mathcal{N}}}}}_{1}\cap {{{{\mathcal{N}}}}}_{2}\,\ne\, {{\emptyset}}\) and

$${{{{\mathcal{N}}}}}_{2}\setminus \{n\}\,\ne\, {{{{\mathcal{N}}}}}_{n}\setminus \{2\}$$
(10)

for all \(n\in {{{{\mathcal{N}}}}}_{1}\cap {{{{\mathcal{N}}}}}_{2}\). Let us consider a graph state \(\left\vert G\right\rangle\) corresponding to a multigraph G that fulfils the above assumptions. To prove that this state cannot be generated in an N-partite quantum network \({{{\mathcal{O}}}}\) we use the inflation method. Specifically, we consider a series of inflations \({{{{\mathcal{I}}}}}_{k}\) (see Fig. 3) of the initial network \({{{\mathcal{O}}}}\), all having the same structure. A non-primed party i (for i ≠ 2) is connected to every other non-primed party j (for j ≠ 2) and to either 2 or \({2}^{{\prime} }\). By Rk and Tk we denote the sets of non-primed parties connected to party 2 and \({2}^{{\prime} }\), respectively. Likewise, we assume that every primed party \({i}^{{\prime} }\) (for \({i}^{{\prime} }\,\ne\, {2}^{{\prime} }\)) is connected to every other primed party \({j}^{{\prime} }\) (for \({j}^{{\prime} }\,\ne\, {2}^{{\prime} }\)) and to either 2 or \({2}^{{\prime} }\); we denote the corresponding sets of parties \({T}_{k}^{{\prime} }\) and \({R}_{k}^{{\prime} }\). However, the exact form of each \({{{{\mathcal{I}}}}}_{k}\) depends on the considered graph state, and so we define it later in the proof.

Fig. 3: Inflations \({{{{\mathcal{I}}}}}_{k}\).
figure 3

Here Tk, Rk and \({T}_{k}^{{\prime} },{R}_{k}^{{\prime} }\) are sets of nonprimed and primed parties, respectively. Every party from a set is connected to all other parties from that set and if two sets are connected then every party from one set is connected to every party from the other set.

Full size image

Having defined \({{{{\mathcal{I}}}}}_{k}\), we can now go on with the proof, which, as in the above example, is by contradiction. Let us consider two operators: g2 given in Eq. (1) and

$${\tilde{g}}_{1}={X}_{1}{Z}_{{2}^{{\prime} }}^{{{{\Gamma }}}_{1,2}}\mathop{\prod}\limits_{k\in {{{{\mathcal{N}}}}}_{1}\setminus \{2\}}{Z}_{k}^{{{{\Gamma }}}_{1,k}}.$$
(11)

While g2 stabilises \(\left\vert G\right\rangle ,{\tilde{g}}_{1}\) is like g1, however, with \({Z}^{{{{\Gamma }}}_{1,2}}\) acting on the party \({2}^{{\prime} }\) instead of 2. This difference between g1 and \({\tilde{g}}_{1}\) produces a commutation relation: \({\tilde{g}}_{1}{g}_{2}={\omega }^{-{{{\Gamma }}}_{1,2}}{g}_{2}{\tilde{g}}_{1}\). Since we also assume Γ1,2 ≠ 0, Lemma 1 yields

$$\mathop{\sum }\limits_{k=0}^{d-1}{\left\langle {\tilde{g}}_{1}^{k}+{g}_{2}^{k}\right\rangle }_{{{{{\mathcal{I}}}}}_{0}}\leqslant\, d+\sqrt{d},$$
(12)

where \({{{{\mathcal{I}}}}}_{0}\) is defined by the set \({T}_{0}=({{{{\mathcal{N}}}}}_{1}\setminus ({{{{\mathcal{N}}}}}_{2}\cup \{2\}))\cup \{1\}\).

The remainder of the proof consists in showing that the assumption that a graph state \(\left\vert G\right\rangle\) can be generated in \({{{\mathcal{O}}}}\) leads to violation of inequality (12). First, using Fact 1 we show that \({\left\langle {\tilde{g}}_{1}\right\rangle }_{{{{{\mathcal{I}}}}}_{0}}={\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{1}}\), where \({{{{\mathcal{I}}}}}_{1}\) is another inflation (cf. Fig. 3) defined by \({T}_{1}={{{{\mathcal{N}}}}}_{1}\cap {{{{\mathcal{N}}}}}_{2}\). We then leverage Facts 1 and 2 to show that \({\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{2}}=1\) implies \({\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{1}}=1\), where \({{{{\mathcal{I}}}}}_{2}\) is an inflation (Fig. 3) defined by T2 = T1⧹{n} for some n ∈ T1. Crucially, we can perform this procedure again for \({n}^{{\prime} }\in {T}_{2}\) which yields

$${\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{3}}=1\quad \Rightarrow \quad {\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{2}}=1\quad \Rightarrow \quad {\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{1}}=1,$$
(13)

where \({{{{\mathcal{I}}}}}_{3}\) is an inflation (Fig. 3) defined by \({T}_{3}={T}_{1}\setminus \{n,{n}^{{\prime} }\}\).

Repeating this procedure \(q=| {{{{\mathcal{N}}}}}_{1}\cap {{{{\mathcal{N}}}}}_{2}| +1\) times produces a chain of implications

$${\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{q}}=1\Rightarrow {\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{q-1}}=1\Rightarrow \cdots \Rightarrow {\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{1}}=1.$$
(14)

This is the main idea of our proof: we start from inflation \({{{{\mathcal{I}}}}}_{1}\) and we gradually make it more and more similar to the original network. In order to see how this is done notice that if \({T}_{q}={{\emptyset}}\) for some q, then \({{{{\mathcal{I}}}}}_{q}\) is an inflation consisting of two copies of the original network. Therefore, since g1 acts nontrivially only on non-primed parties, by tracing out all primed parties we get \({\langle {g}_{1}\rangle }_{{{{{\mathcal{I}}}}}_{q}}={\langle {g}_{1}\rangle }_{{{{\mathcal{O}}}}}=1\), if we generated \(\left\vert G\right\rangle\) in \({{{\mathcal{O}}}}\). This implies \({\left\langle {\tilde{g}}_{1}\right\rangle }_{{{{{\mathcal{I}}}}}_{0}}=1\), and so \({\tilde{g}}_{1}\) is a stabilizing operator of a state generated in \({{{{\mathcal{I}}}}}_{0}\), meaning that \({\langle {\tilde{g}}_{1}^{k}\rangle }_{{{{{\mathcal{I}}}}}_{0}}=1\) for all k.

One can show that g2 is a stabilizing operator of the state generated in \({{{{\mathcal{I}}}}}_{0}\), therefore \(\langle {g}_{2}^{k}\rangle =1\) for all k. Consequently, the left side of (12) equals 2d, leading to a contradiction. □

Using the standard continuity argument one can extend the above result to any state that is sufficiently close to a graph state. Indeed, denoting \(F(\rho ,\left\vert \psi \right\rangle )=\left\langle \psi \right\vert \rho \left\vert \psi \right\rangle\), we can formulate the following theorem (see Supplementary Note 5 for a proof).

Theorem 2

Let us consider a state ρ and a graph state \(\left\vert G\right\rangle \in {{\mathbb{C}}}_{d}^{\otimes N}\), where d is prime. Moreover, let \(q=| {{{{\mathcal{N}}}}}_{1}\cap {{{{\mathcal{N}}}}}_{2}| +1\) for graphs G that fulfil (10) and q = 1 in other cases. If

$$F(\rho ,\left\vert G\right\rangle )\, >\, 1-\frac{1}{8}\left({\beta }^{2}+2\gamma -\beta \sqrt{{\beta }^{2}+4\gamma }\right),$$
(15)

where β = 2q − 1 and \(\gamma =(d-\sqrt{d})/(d-1)\), then ρ cannot be generated in a LOSR network with bipartite sources.

Clearly, increasing q increases the value of the expression on the right side of the inequality. Therefore, to maximize the number of states covered by the above theorem, it is beneficial to take the smallest q possible. As an example, let us consider the graph state corresponding to the graph presented on Fig. 1. Here q = 1, d = 3, and so (15) simplifies to \(F(\rho ,\left\vert G\right\rangle ) > 0.952\). Interestingly, the bound (15) can be relaxed by increasing d; in the limit d → ∞ for q = 1 we obtain \(F(\rho ,\left\vert G\right\rangle )\, >\, 0.905\).

Discussion

We showed classical communication between parties is necessary for the generation of qudit graph states of prime local dimension (and all states that are in their vicinity) in quantum networks with bipartite sources. We achieve this goal by employing the quantum inflation method. In fact, we demonstrate that the use of many different inflations of the same network might be beneficial over using just two inflations as done before in the literature, and hence our work might inspire future research involving quantum networks. Our results serve as a guide to experimental physicists who wish to implement protocols on quantum networks that involve graph states. On the other hand, they hint at a possible gain from the construction of protocols based on other states than the graph states.

Still, many questions concerning LOSR networks remain unexplored. The most obvious one is whether graph states are preparable with k-partite sources for k ⩾ 3. Even if from the application viewpoint this case seems less important than that of k = 2, answering this question would allow us to understand quantum networks on a deeper level. One can also ask whether other classes of multipartite states can be obtained in LOSR networks. Apart from the graph states, this question was answered negatively for symmetric or antisymmetric states of any local dimension19 and pure genuinely entangled states of local dimension 2 and 3 in ref. 20. On the other hand, it would be interesting to determine the minimal amount of classical communication required to generate graph states in LOCC networks and to identify other classes of states that are efficiently preparable in this sense.

Lastly, let us note here that while finishing this manuscript, we became aware of a related work by Y.-X. Wang et al.37, where the analogous statement to our Theorem 1 has been derived for all qubit, and a subclass of qudit graph states. While the proof in37 covers only a subset of graph states in the case d > 2, this includes some qudit graph states where the local dimension is not a prime number, which are not covered by our Theorem 1. Moreover, the inequality from37 used to formulate the proof (analog of Lemma 1), allows the authors to derive a fidelity bound for the said subset of graph states that performs significantly better for small d than the one we provide in Theorem 2.