Introduction

The fundamental insight of spin polarization effects originating from local asymmetry in non-magnetic materials with inversion has led to the new finding of a hidden form of the Rashba effect1,2. Conventional Rashba effect (R-1) is induced by the breaking of global inversion symmetry. The spin-orbit coupling (SOC) combined with a potential gradient from an asymmetric system induces spin-polarized electronic states with helical spin texture, called spin-momentum locking, as illustrated in Fig. 1a3,4. In this respect, the spin polarization of centrosymmetric crystals was previously unnoticed and overlooked. Recently, however, it has been substantiated theoretically and experimentally that these spin polarization effects can emerge from the local asymmetry in the atomic configuration rather than the crystal space group, leading to the hidden Rashba effect (R-2)1,2,5,6,7,8,9. In a centrosymmetric system, all bands must be doubly degenerate guaranteed by inversion symmetry, but the opposite spin polarizations or the inversion partners in these doubly degenerate bands are spatially separated into two sectors (e.g., top and bottom sublayers) resulting in spin-layer locking (SLL).

Fig. 1: The Rahsba effect and spin texture in nonmagnetic materials.
figure 1

a R-1 Rashba effect in non-centrosymmetric materials and (b) R-2 Rashba effect and (c) unconventional R-2 Rashba effect in the centrosymmetric system. The spin textures of the inner and outer bands are shown for constant energy contour corresponding to the yellow dashed line in each image. The spin textures induced by R-2 Rashba effects are spatially separated in α- and β-sectors with opposite helicities.

Full size image

In the R-1 effect, since the inversion symmetry (IS) is broken but the time-reversal symmetry (TRS) is maintained, the Rashba bands must be doubly degenerate at time-reversal invariant momenta (TRIM) to satisfy Kramers’ degeneracy. Thus, the inner and outer Rashba bands must intersect at TRIM as shown in Fig. 1a. The R-2 effect, on the other hand, has a greater degree of freedom in the shape of the band than the R-1 effect. In R-2 systems, the inner and outer bands do not need to meet at TRIM since both IS and TRS enforce each band to be doubly degenerate, and thus they can be separated. Some studies showed that R-2 bands are indeed composed of two individual parabolic bands2,6, whereas some other R-2 bands exhibit dispersion like the R-1 type9. It is clear that the R-2 effect may have more diverse Rashba band configurations than the R-1 effect. It is, therefore, suggested that such Rashba band diversity would be utilized in a new step of spin-splitting engineering.

Here, we propose a mechanism to control the spin helicity of the R-2 effect. In general, both the R-1 and R-2 effects present opposite spin helicities in the inner and outer bands as depicted in Fig. 1a, b. However, in our newly proposed R-2 system, both the inner and outer bands exhibit the same spin helicity. The starting point of our idea is to consider two pairs of two degenerate R-2 bands as shown in Fig. 1c rather than a pair of bands, which get involved in the conventional (hidden) Rashba effects. (We assume that the bands are valence-like, but the same reasoning applies to the conduction-like bands.) Due to the aforementioned band diversity of the R-2 bands, all four Rashba bands can contribute to the unconventional R-2 effect. In materials with strong spin-orbit coupling, band inversion may occur between the inner band of the higher-energy R-2 pair and the outer band of the lower-energy R-2 pair resulting in the two Fermi circles at the top of the bands that have spin textures with the same helicity at each spatial sector. The synopsis of the inverted R-2 bands and their spin textures are illustrated in Fig. 1c. In the following, we will demonstrate the unconventional R-2 effect exhibited in InTe chosen as a model system.

Results and discussion

Crystal and electronic structures

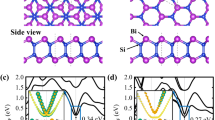
III-VI mono chalcogenides denoted as MX are composed of group III post-transition metal element M (M = Ga or In) and group VI chalcogen element X (X = S, Se, or Te). They are van der Waals layered materials with an atomic configuration of X-M-M-X, where two metal atoms M are sandwiched between two chalcogen atoms X. It has been known that the monolayer of this material forms two crystal phases. The one, which has been more studied, is the phase with mirror symmetry displaying the upper and lower chalcogen atoms in the same column along the c-axis10, as shown in Supplementary Fig. 1. The other phase in which the upper and lower chalcogen layers are relatively rotated by \({60}^{\circ }\) (or \({180}^{\circ }\)) has also been experimentally discovered and reported theoretically11,12,13,14. This structure has inversion symmetry called a trigonal anti-prismatic structure. The top and side views of this centrosymmetric monolayer are shown in Fig. 2a. Their structural relation is reminiscent of that between the trigonal prismatic (H) and octahedral (T) phases of transition-metal dichalcogenide (TMD) systems. Here we focus on the inversion symmetric system and take InTe as an exemplary material to demonstrate the unconventional R-2 effect.

Fig. 2: Crystal and electronic structures of InTe.
figure 2

a Top and side view of the crystal structures of monolayer InTe with inversion symmetry. b Electronic band structures of monolayer InTe, of which valence bands near the Γ point are shown in insets. The inset shows relevant four bands labeled from VB2 to VB5. c–f Spin textures, which are spatially resolved on the top and bottom Te sublayers, marked on the constant energy contours of the inner and outer bands. g Degree of wavefunction segregation (DWS) evaluated for spin up at VB3 along \({{\bf{k}}}_{\Gamma -{\rm{K}}}\). The inset shows the wavefunction squared at three different \({\bf{k}}\) points.

Full size image

The electronic band structure of InTe with spin-orbit coupling is shown in Fig. 2b. The inversion symmetry imposes double degeneracy of each band, which means that the net spin polarization of each band remains trivial. By inspecting the spin polarization projected onto the top and bottom Te sublayers, however, we found that there exists nontrivial spin splitting in the valence band 2 (VB2) and VB3 denoted in the inset of Fig. 2b. The spatially resolved spin textures of different Fermi circles around the Γ point for two different Fermi energy are shown in Fig. 2c–f. At each Fermi energy, the spin textures projected on the top and bottom Te sublayers show the opposite helicities. Interestingly, the relative spin helicities of VB2 and VB3 at the higher-energy Fermi circles shown in Fig. 2c, d, are parallel near the Γ point, which is an unconventional spin texture unexpected in other R-2 materials. On the other hand, the relative spin helicities at the lower-energy Fermi circles shown in Fig. 2e, f are antiparallel as observed in other R-2 materials, since they are the inversion partners of each other.

Another atypical behavior was also observed in the SLL phenomenon. We scrutinized the spin-resolved wavefunctions of VB3 for several k values and found that there exists the transition of wavefunction segregation quantified by \({\rm{DWS}}\left({\psi }_{n{\bf{k}}}^{\sigma }\right)\), which is defined as Eq. 3 given in the Methods section, as shown in Fig. 2g. For instance, \({\big|{\psi }_{{\rm{VB}}3{\boldsymbol{,}}{\bf{k}}}^{\uparrow }\big|}^{2}\) is segregated on the top sublayer at small k, e.g., at k1. However, it evolves toward comparable spatial segregation or \({\rm{DWS}}\left({\psi }_{n{\bf{k}}}^{\sigma }\right)=0\) at k2, and then back to strong spatial segregation on the bottom layer at large k, e.g., at k3.

The unique Rashba spin polarization phenomenon of InTe is hardly understood in terms of the conventional types of Rashba bands. Since the system possesses inversion symmetry, we can rule out the possibility of R-1 type spin splitting. The other option is R-2 type spin splitting. Indeed, InTe exhibits SLL, which is a hallmark phenomenon in the R-2 effect. However, the inversion of spin helicity of the inner band and the transition of SLL cannot be explained by the R-2 type Rashba mechanism.

Unconventional hidden Rashba spin splitting

To understand the anomalous spin helicity at VB2 and VB3, we explored the projected spin polarization onto the top and bottom Te sublayers. Helical spin textures indeed emerge in each Te sublayer with opposite helicities, resulting from the spin-layer locking. The spin texture of VB2 maintains a uniform helicity, while the spin texture of VB3 changes its direction as k increases, as displayed in Fig. 3a, b. This result is consistent with the spin configuration behavior of different Fermi energies of VB2 and VB3 shown in Fig. 2c–f: the same helicity direction near the Γ point, different directions far away. Thus, the anomalous spin helicity is due to the strange behavior of the spin texture of VB3.

Fig. 3: Spatially resolved spin textures of the unconventional R-2 Rashba bands.
figure 3

a–d Spin textures on VB2 ~ VB5 that are spatially resolved on the top Te sublayer around the Γ point. e Spin textures plotted on the four unconventional R-2 Rashba bands. Red (blue) arrows represent the counterclockwise (clockwise) spin helicity. The size of the arrows and the colormap indicate the in-plane spin components and energy scale in eV relative to the Fermi energy, respectively.

Full size image

Intriguingly, we found that there is another set of non-trivial Rashba bands VB4 and VB5. They are placed just below VB2 and VB3 as indicated in the inset of Fig. 2b. Their projected spin polarizations onto the top Te sublayer are shown in Fig. 3c, d. Again, a peculiar configuration of spin polarization is observed in VB4. It does not exhibit a homogeneous texture but alters its helicity when deviating from the Γ point. Accompanying this behavior, the transition of wavefunction separation also occurs in VB4 as in VB3, as shown in Supplementary Fig. 2. Taken together, we have four Rashba bands with spin texture spatially resolved on the top and bottom Te sublayers, as shown in Fig. 3e. Also, the spin textures of the corresponding bands for the entire Brillouin zone are shown in Supplementary Fig. 3. To verify that these anomalous spin textures are not functional-dependent artifacts, we also employed the HSE06 exchange-correlation functional, which produces four corresponding Rashba bands as shown in Supplementary Fig. 4.

Based on our understanding of the R-2 effect and the arrangement of the bands, VB2/VB3 must form an R-2 pair, and VB4/VB5 another. If VB2 and VB3 form an R-2 pair, they must have opposite spin helicities, but this relationship breaks down near the center of the Brillouin zone. The same relationship also applies to VB4/VB5 pair. Such an expected arrangement of band pairs is observed far from, but not near the zone center. To satisfy the R-2 relationship near the Γ point as well, VB2 and VB4 seem to pair up and so do VB3 and VB5 instead. Thus, if pair switching occurs when it deviates from the Γ point and returns to the original pair, then this phenomenon can be explained consistently. The only way to make this possible would be the band inversion between VB3 and VB4.

Origin of unconventional R-2 type spin splitting

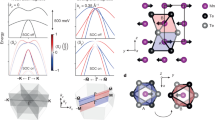
To verify our speculation on such an unconventional R-2 effect, we first considered an artificial structure made of a Te-In half sublayer with broken inversion symmetry. A hydrogen atom was introduced to passivate the spurious dangling bond of each In atom, as illustrated in the inset of Fig. 4a. Its electronic band structure was calculated in the absence of SOC as shown in Fig. 4a. It exhibits two topmost valence bands with different curvatures near the Γ point, commonly called heavy and light hole bands, to which the in-plane p orbitals of the Te atom mainly contribute. It was found that when two such half sublayers are combined to form a Te-In-In-Te monolayer with inversion, two pairs of such topmost valence bands, each pair from each half sublayer, would form two four-fold degenerate valence bands without considering the sublayer-sublayer interaction (SSI). In reality, the unavoidable SSI lifts the four-fold degeneracy to form four doubly degenerate bands just below the topmost valence band resulting in the band inversion between the heavy-hole band in one sublayer and the light hole band in the other one even in the SOC-free electronic band structure of the InTe monolayer as shown in Fig. 4b. It is noted that the band structure exhibits band crossings due to the difference in curvature of the two original bands in the half sublayer as well as avoided band crossings due to the SSI. The light-hole band in the high energy set and the heavy-hole band in the low energy set intersect each other, followed by anti-crossing along the Γ-K line. However, the bands still cross over along the Γ-M line. When SOC is turned on, as illustrated in Fig. 4c–f, degeneracies at these crossing points as well as at the gamma point are further lifted to eventually form four separate R-2 bands VB2/VB3 and VB4/VB5 shown in the inset of Fig. 2b. Each R-2 band is still doubly degenerate guaranteed by inversion symmetry. Note that the topmost valence band in Fig. 4b, which is not of interest in this study, originates from the blue (Te \({p}_{z}\) orbital dominant) band in Fig. 4a.

Fig. 4: Role of spin-orbit coupling and the formation of unconventional R-2 effect.
figure 4

a, b The local orbital projected electronic band structure of (a) half sublayer and (b) monolayer of InTe without SOC. Their zoomed-in bands near the Γ point are shown in the corresponding insets. The artificial half sublayer structure is shown in the inset of (a). c–f The evolution of the band structure of the monolayer InTe according to the strength of SOC. g–j Schematic band diagrams illustrating the formation of four unconventional R-2 Rashba bands. The sublayer-sublayer interaction energy denoted by \({\Delta E}_{I}\) is represented in (h). R-2 Rashba pairs and spin polarizations of each sector are shown in the final step (j).

Full size image

These gluing and deforming processes of these R-2 bands are illustrated in Fig. 4g–j. SOC not only lifts the four-fold degeneracy and induces four independent bands, but also increases the level repulsion between them, so it plays a decisive role in forming four well-separated bands. This is reminiscent of the band inversion scenario in topological insulators15. The inversion of the band parity played an important role there, but the inversion of the spin character plays a role here. By tracking the spin polarization of each sector, we can understand how the spin configuration is arranged and reach the spin texture of a monolayer. Essentially, the band inversion leads to R-2 type Rashba pair switching and the transition of spin helicities. Meanwhile, SOC introduces the hybridization of the heavy and light characters. At strong SOC, furthermore, the traces of band crossing fade away and the inversion of spin polarization is concealed. This leads to the last stage, Fig. 4j, which is essentially the same as the unconventional R-2 band of the form proposed in Fig. 1c. We further notice that strong SOC is a crucial factor for hidden Rashba spin splitting as pointed out by9. By adjusting the strength of SOC, we confirmed that wavefunctions are strongly segregated and R-2 SLL is also intense, as shown in Supplementary Fig. 5. It is also known that the hidden Rashba effect is substantially affected by the competition between SOC and SSI. To understand this, we set up the model Hamiltonian described in Supplementary Note 1 and fitted the DFT results to confirm that SSI was suppressed as SOC increased, as shown in Supplementary Fig. 6. It is, therefore, the presence of strong SOC and band inversion that is the physical origin of the formation of the unconventional R-2 effect.

In summary, we developed a new type of Rashba spin splitting of centrosymmetric systems by exemplifying the InTe monolayer as a model system using first-principles density functional theory. We demonstrated sequentially how a new behavioral band was formed, starting with the half sublayer by breaking up the monolayer, and revealed that the band inversion and hybridization between two sets of R-2 bands can lead to the unconventional Rashba band structures. A new kind of Rahsba band, which differs from conventional R-2 bands, possesses two Fermi circles with the same helicity. Thus, we expect that wide spin-filtering energy windows can be achieved experimentally from this unconventional R-2 effect. As a potential application, the efficiency of spin-to-charge conversion could be improved using the unconventional R-2 effect. It has been reported that the conventional Rashba bands’ opposite spin texture partially compensates for their respective contributions to the spin-to-charge conversion while also suppressing its efficiency16. The two Fermi circles from the unconventional hidden Rashba effect are expected to both significantly contribute to the spin-to-charge conversion and so induce the substantial inverse Rashba-Edelstein Effect with a high efficiency17. We also expect that the predicted unconventional hidden Rashba effect can be observed by spin- and angle-resolved photoemission spectroscopic (spin-resolved ARPES) measurements. There are results of direct observation of the R-2 effect and spin layer locking phenomenon using spin-resolved ARPES in two-dimensional materials with inversion symmetry, such as PtSe2 monolayer and WSe2 bilayer2,5,6. InTe’s unconventional R-2 effect is also expected to be experimentally measured with the same technique. Our results not only demonstrate a monolayer InTe to possess unconventional R-2 bands, but also provide an exciting platform to explore the intriguing spin polarization physics from hidden Rashba effects.

Methods

Density functional calculation

Structural relaxations and electronic structure calculations were carried out using density functional theory as implemented in the Vienna ab initio simulation package (VASP)18. The electronic wavefunctions were expanded by plane wave basis with a kinetic energy cutoff of 500 eV. The generalized gradient approximation (GGA) of Perdew−Burke−Ernzerhof (PBE) is used for the exchange-correlation potential. PBE-based results are validated using hybrid functional (HSE06) to rule out any functional-related artifacts19. A sufficiently large vacuum layer >20 Å is used to avoid interactions between the nearest slabs. The Brillouin zone (BZ) of each structure was sampled using a 15 × 15 × 1 k-point mesh according to the Monkhorst-Pack scheme20.

Manipulation of spin-orbit interaction

The SOC is described by the following Hamiltonian

$${H}_{{SOC}}^{\alpha \beta }=\frac{{{{\hslash }}}^{2}}{{(2{mc})}^{2}}\frac{K(r)}{r}\frac{{dV}(r)}{{dr}}{{\boldsymbol{\sigma }}}^{\alpha \beta }\,\cdot \,{\bf{L}},$$
(1)

where \(\alpha\) and \(\beta\) indicate spin-up and -down components of the spinor wave function, \({\boldsymbol{\sigma }}\) and \({\bf{L}}\) are Pauli spin matrices and angular momentum operator. \(V(r)\) is the spherical part of the effective all-electron potential within the PAW sphere and \(\scriptstyle {K\left(r\right)=\,{\left(1-\frac{V(r)}{{(2{mc})}^{2}}\right)}^{-1}}\). To examine the effect of the SOC strength, an artificial parameter λ was introduced to scale the SOC Hamiltonian as

$${H}_{{\rm{SOC}}}^{\alpha \beta }(\lambda )=\frac{\lambda }{{\lambda }_{0}}{H}_{{\rm{SOC}}}^{\alpha \beta },$$
(2)

where \({\lambda }_{0}\) is the real SOC strength.

Visualization of spin texture and spin-layer locking

The spin polarization was evaluated as the expectation value of the spin operator given by \({{\boldsymbol{\mu }}}_{n{\bf{k}}}\propto \,\left\langle {\psi }_{n{\bf{k}}}|{\boldsymbol{\sigma }}|{\psi }_{n{\bf{k}}}\right\rangle\) where \({\boldsymbol{\sigma }}\) is the Pauli spin matrix vector. Its projection on each atom \(a\), \({{\boldsymbol{\mu }}}_{n{\bf{k}}}^{a}\) was obtained by expanding \({{\boldsymbol{\mu }}}_{n{\bf{k}}}\) in terms of the spherical harmonics \(|{Y}_{l}{m}^{a}\rangle\) with orbital angular momentum \(\left(l,m\right)\) of the \(a\) atom, or \({{\boldsymbol{\mu }}}_{n{\bf{k}}}\propto \,{\sum }_{{lm}}\left\langle {\psi }_{n{\bf{k}}}|{\boldsymbol{\sigma }}|{Y}_{{lm}}^{a}\right\rangle \left\langle {Y}_{{lm}}^{a}|{\psi }_{n{\bf{k}}}\right\rangle\).

To demonstrate the SLL and quantify the spatial spin separation, we introduced the degree of wavefunction segregation \({\rm{DWS}}\left({\psi }_{n{\bf{k}}}^{{\boldsymbol{\sigma }}}\right)\) defined as21

$${\rm{DWS}}\left({\psi }_{n{\bf{k}}}^{\sigma }\right)=\left|\frac{{P}_{{\psi }_{n{\bf{k}}}^{\sigma }}({S}_{\alpha })-{P}_{{\psi }_{n{\bf{k}}}^{\sigma }}({S}_{\beta })}{{P}_{{\psi }_{n{\bf{k}}}^{\sigma }}\left({S}_{\alpha }\right)+{P}_{{\psi }_{n{\bf{k}}}^{\sigma }}({S}_{\beta })}\right|,$$
(3)

where \({P}_{{\psi }_{n{\boldsymbol{k}}}^{\sigma }}({S}_{\alpha })\) is the component of the wavefunction \({\psi }_{n{\boldsymbol{k}}}^{\sigma }\) localized on the sector \({S}_{\alpha }\)

$${P}_{{\psi }_{n{\bf{k}}}^{\sigma }}\left({S}_{\alpha }\right)=\mathop{\int }\limits_{\varOmega \in {S}_{\alpha }}{\left|{\psi }_{n{\bf{k}}}^{\sigma }({\bf{r}})\right|}^{2}{d}^{3}{\bf{r}}.$$
(4)